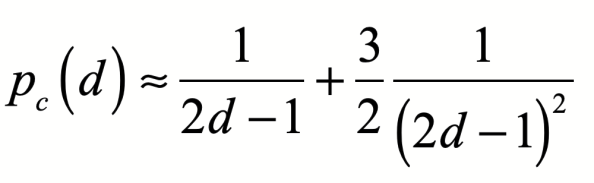我们生活在三维空间的经验或许限制了对高维空间的想象。事实上,不止弦理论在十维空间运行,几乎每一种复杂的动力系统都在高维状态空间中被描述。一旦三维偏见消除,我们会发现,生命在适应性景观的演化,机器学习在数千个维度上最小化目标函数,都可以理解为是沿着适应性网络的随机游走。
关键词:复杂系统,高维空间,随机游走,渗流理论,自然演化,机器学习,复杂网络
David D. Nolte | 作者
刘志航 | 译者
梁金 | 审校
高维物理学正在成为现代动力学的规范。不仅是弦理论在十维空间(加上一个时间维度)运行,而且几乎每一种复杂的动力系统都在高维状态空间中被描述和分析。例如,群体动力学(population dynamics)可能描述成百上千个不同的物种,每个物种的时变种群在高维空间中定义一个单独的轴;耦合机械系统同样可能有成百上千(或更多)的自由度,在高维相空间中被描述。
由于这些原因,随着今天的物理学越来越多地涉及到高维动力学的挑战和问题,我们需要工具帮助对高维系统极不直观的行为有直观感觉。
快速发展的机器学习领域经常处理需要最小化的高维景观(损失函数或目标函数),高维度通常被称为负面的“维度灾难”(Curse of Dimensionality)。
维度可能被看作是一种灾难,原因有几个。首先,几乎不可能在高于 d=4 的维度上实现数据可视化(第四维度有时可以用颜色或时间序列进行可视化)。其次,过多的自由度会产生太多变量来拟合或建模,导致典型的过拟合问题。简单地说,高维空间大得离谱。第三,我们对面积和体积之间关系的直觉受到三维经验的影响,导致对高维空间几何对象的理解产生严重偏颇。发生在三维空间的物理过程被过度泛化,导致人们产生先入为主的、在高维空间中并不成立的概念。
以随机游走为例。它通常从一维随机游走(抛硬币)开始讲授,然后扩展到二维,再到三维……大多数教科书都到此为止。但在复杂系统中,高维随机游走是常规而非例外。在这方面特别重要的一个例子是分子演化(molecular evolution)问题。基因组上的每个位点都代表一个独立的自由度,分子演化可以被描述为在这个空间中的随机游走,但是所有可能基因突变的空间是巨大的。面对这样天文数字般巨大的组合,很难想象随机突变如何创造出像 ATP 合成酶这样复杂的东西,而 ATP 合成酶是所有高等生物能量学的基础。幸运的是,这个难题的答案在于物理学中的高维随机游走。
这篇文章介绍十维空间随机游走的物理学。实际上,十维与九维、十一维或二十维相比并没有什么特别之处,但由于几个原因,它为高维物理学提供了一个方便示范。
首先,它比三维空间高得多,即使利用投影也无法有效地可视化,所以它迫使我们与高维空间固有的“不可视化”相抗衡。第二,十维空间足够大,以至于它的行为与任何高维空间大致相同,至少在涉及随机游走时是如此。第三,它与计算机的典型内存大小所能处理的大小差不多。例如,一个十维超立方晶格(hyperlattice),沿每个维度有10个离散点,有1010个晶格点(100亿或10G),这大约是一个典型的计算机用内部存储器所能处理的极限。
作为可视化的起点,让我们从众所周知的四维超立方体(hypercube)开始,但将其扩展为四维超晶格,每个维度上有三个值,而不是两个。由此产生的四维晶格可以在二维上显示为一个具有34=81个节点和216个链接或边的网络。其结果如图1所示,在二维中表示为一个有节点和边的网络图。每个节点有四个与邻居节点的链接。尽管这个图有明显的三维外观,但如果你仔细观察,会发现在试图与四个邻居链接时出现的挫折感(frustration),从而出现许多长距离的链接。
图1. 四维超晶格,沿4个维度各有三个点。这个高维离散晶格被表示为一个具有节点和边的二维网络图。
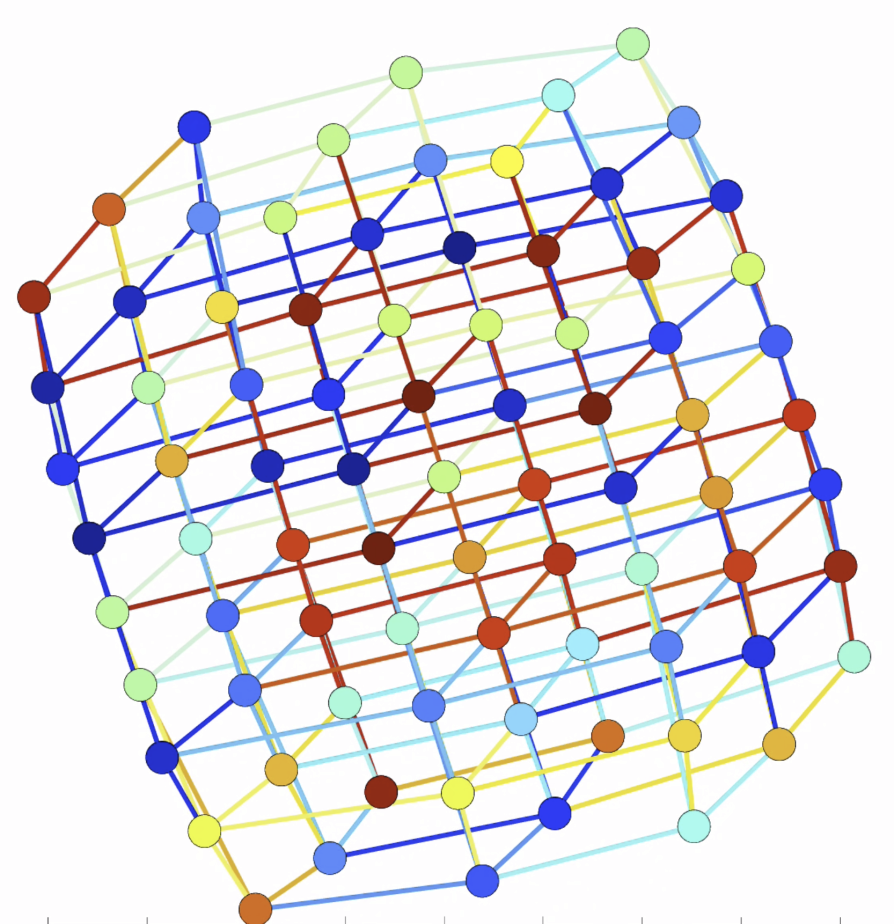
我们还可以看到具有 210 = 1024 个节点和 5120 条边的十维超立方体,如图 2 所示。当以二维方式呈现时,有点难以看到超立方体的对称性,但每个节点正好有10个链接。
图2. 一个有 1024 个节点和 5120 条边的十维超晶格。每个节点有正好10条与邻居节点的链接。
将这个十维晶格扩展到 10 个位点而不是 2 个位点并试图将其可视化,这令人望而却步,因为由此产生的二维图看起来就像一大堆重叠的圆圈。然而,我们的兴趣不仅仅是扩展到每个维度10个位点,而是扩展到无限数量的位点。这就是我们想要探索随机游走物理学的十维无限晶格。
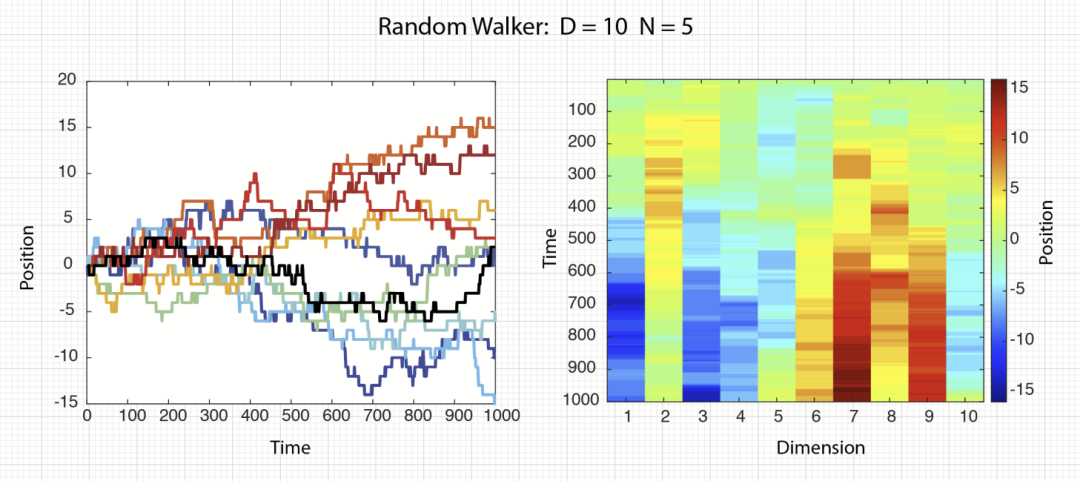
十维的无约束随机游走只是一维简单随机游走的最小扩展。因为每个维度都是独立的,在每次迭代中,单个随机游走者沿着10个维度中的任何一个随机迈出一步,因此在10个维度的任何一个中的运动都只是一维随机游走。因此,在十维中可视化这种随机游走的方法,是简单地绘制每个维度上的游走,如图3所示。游走者在每个时间点沿着任何给定维度迈出 +1 或 -1 步的几率为十分之一。
图3. 单个游走者在10个维度上每次迈出随机一步。图中显示了所有十个维度的游走者的位置作为时间的函数。
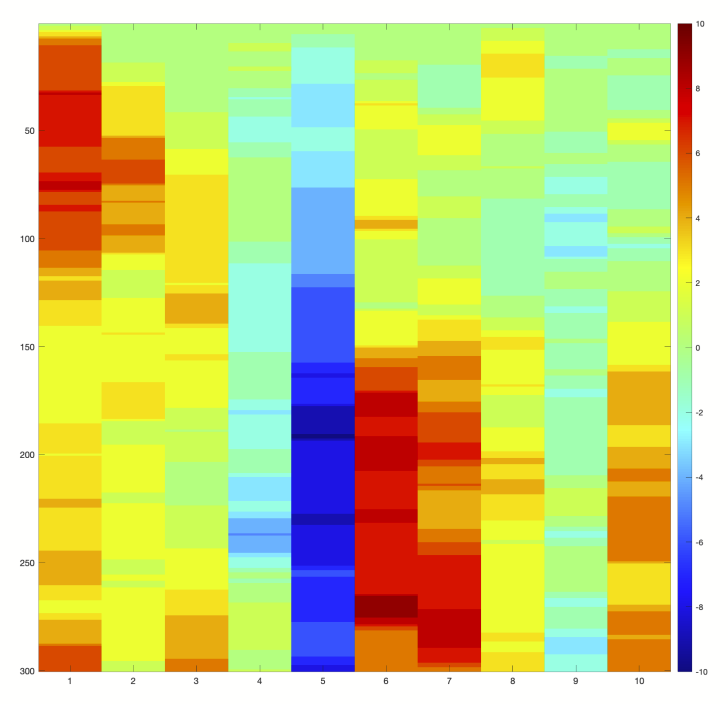
对于图3相同的数据,十维随机游走者的另一种可视化如图4所示。在这种情况下,位移用颜色编码,每一列表示不同维度。纵轴表示时间(从顶部开始,向下增加)。这种类型的热力图可以很容易地扩展到数百个维度。每一行都是十维空间中单个游走者的位置向量。
图4. 与图3中的数据相同,在超晶格上的单个十维随机游走者。距离用颜色编码。时间在纵轴上(向下增加)。每一行是一个十维位置向量,这个表示法是单个十维空间轨迹。
在十维超晶格中,所有的晶格点在每个时间点都是可以访问的,所以没有任何约束可以阻止以前访问过的节点。有一种可能的调整,可以防止重走访问过的路径。这就是所谓的自我规避行走(self-avoiding-walk, SAW)。
在二维空间,普通随机游走和自我规避行走的几何和动力学特性有很大区别。然而事实证明,在大于四维空间中,去不同区域有如此多的可能性(高维空间有如此多的自由空间),随机游走极不可能与自己交叉。因此,在十维超晶格中,我们不需要区分普通游走和自我规避行走的区别。然而,还可以施加其它约束,模仿复杂系统在时间上的演化,这些约束可以产生重要后果,正如我们接下来看到的。
在无限超晶格中,所有晶格点都是一样的,可以平等访问。然而,在复杂系统研究中,为高维晶格的每个节点分配一个值是很常见的:
• 这个值可以由一个势能函数决定,在晶格几何上产生一个高维势能景观;
• 或者这个值可能是一个物种的生存适应性,产生一个高维适应性景观,支配着物种的竞争和演化;
• 或者该值可能是多变量分析或机器学习中最小化问题的损失函数(一个目标函数)。
在所有这些情况下,节点上的标量值定义了一个状态点游走的景观。那么问题来了,高维景观有什么特性,它如何影响随机游走者?
作为例子,我们考虑一个完全随机的点对点的景观。在这个景观中没有任何关联,使它变得最大限度地粗糙。然后,我们要求一个随机游走者在这个景观中沿着等势能面行走,不增加也不减少其势能。从我们生活在三维空间的空间直觉出发,可能担心这个游走者会很快被限制在景观的某些区域。想像一张画有轮廓线的二维地形图——从山边的某个海拔高度开始,如果我们必须沿着保持海拔高度的方向行走,就会停留在一个特定等高线上,最终在绕过山峰后回到起点,我们被困住了!这就是我们的直觉!但是,这种由三维生活告知的直觉具有误导性。在十维超晶格中会发生什么?
为了使这个例子易于分析,我们假设势能函数被限制为 N 个离散值。这意味着在一个给定游走者节点的 10 个邻居中,平均只有10/N可能具有与给定游走者节点相同的势能。这就限制了游走者的可用节点,并将均匀超晶格转换成超晶格位点渗流问题。
渗流理论(percolation theory)是统计物理学中一个迷人的话题。有许多深刻的概念来自于对网络中节点如何连接这一简单问题的提问。渗流理论的最重要方面是渗流阈值的概念。从一个端对端连接的完整网络开始,随机地移除节点,当被移除节点达到一个临界比例(平均)时,将不再有一个跨越网络的单一连接团簇,这个临界比例被称为渗流阈值。在渗流阈值以上,随机游走者可以从网络的一部分到达另一部分。低于渗流阈值,随机游走者就会被限制在一个局部团簇中。
如果一个超晶格的景观势能(或高度、等高线)有N个离散值,如果一个随机游走者只能移动到与当前势能值相同的位置(保持在水平集合上),那么只有一部分超晶格位点对游走者来说是可及的,而游走者是否能找到一条跨越超晶格的路径的问题,就变成了可及位点比例与渗流阈值的关系问题。
超晶格的渗流阈值众所周知。对于高维度来说,可以很准确地给出公式:
其中 d 是超晶格维度。对于十维超晶格来说,渗流阈值是Pc(10)=0.0568,或大约6%。因此,如果超晶格中超过6%的位点与游走者的当前位点具有相同的值,那么游走者就可以在超晶格中自由漫游。
如果势能有 N=5 个离散值,那么20%的位点是可及的,这高于渗流阈值,游走者可以走得尽可能远。无论初始势能值是什么,这个陈述都是正确的。它可能是5,这意味着游走者在景观上的高度最高。或者它可能是1,这意味着游走者在景观上的高度最低。然而,即使在最高处,如果可及位点比例高于渗流阈值,那么游走者也可以停留在高高的山脊上,跨越景观。如果从山谷最低处开始,情况也是如此。因此,山脊非常普遍,深谷也是如此,但它们允许在景观上自由移动。
另一方面,所谓的山峰将对应势能值5,被4或更低的势能值包围。在十维空间发生这种情况的几率为 0.2*(1-0.810) = 0.18。所以,在具有5个势能值的十维超晶格中,山峰的总密度仅为18%。因此,在十维空间中,山峰很罕见,而山脊很常见。在更高维度,渗流阈值随维度大致成反比下降,山峰变得极为罕见,在景观游走中几乎不发挥作用。
为了说明这一点,图5是与图2相同的十维网络,但只显示了 N=5 时共享相同数值的节点,这意味着只有 20% 的节点可以被只停留在相同数值节点上的游走者访问。有一个“最大团簇”(giant cluster)保持连接,横跨初始网络。如果初始网络是无限的,那么这个巨大的团簇也是无限的,但包含有限的一部分节点。
图5. 一个横跨图2中网络的十维团簇,1/5的节点共享相同的景观势能值。这个团簇代表一个横跨空间的山脊。另外还有四个并存的团簇,每个团簇都分别跨越了同一个十维空间。
随机游走的定量细节可能会根据子网络(簇、脊或水平集合)与渗流阈值的接近程度而变化。例如,图 6 显示了一个 D=10,N=5 的随机游走者。扩散速度比图3和图4的无约束游走要慢一些。但在十维空间内的游走能力得到了保留。
那么,这就是重要结论:在高维景观中,山脊比山峰要常见得多。这对生命演化、复杂系统动力学以及机器学习的威力都有深远影响。
当高维空间是基因组上可能的突变空间,当景观是适应性景观,为一个突变分配相对于其他突变的生存优势,那么随机游走描述物种的跨代演化。
高维空间普遍存在的山脊,或更普遍的水平集合,对演化过程有重大影响,因为一个物种可以沿着水平集合游走,获得许多可能的突变,这些突变对物种的生存能力只有中性影响。同时,基因构成在这个“中性网络”中不断漂移,使该物种的基因组能够进入空间的遥远部分。然后,在某些时候,自然选择可能会使该物种登上附近(罕见)的高峰,而该物种就达到了新的平衡。
早期对适应性景观的一个(错误)批评,是物种要从一个适应性高峰移动到另一个高峰,就必须向下走,穿过宽阔的适应性低谷,才能到达另一个高峰。但这是三维空间思维的遗留。在高维空间,中性网络无处不在,突变可以离开一个适应性高峰到达一个中性网络(这可以通过随机游走进行采样),直到状态接近某个遥远的高峰。不再有必要从适应性高峰和低谷的角度来思考——只是随机游走。然后,一旦我们的三维偏见消除,极其复杂结构(如ATP合成酶)的演化,可以被理解为沿着近乎中性的适应性网络的随机游走。
同样的论点也适用于机器学习,特别是深度学习中的许多情况。在训练深度神经网络时,可能有成千上万的神经权重需要通过最小化损失函数(也被称为目标函数)来训练。损失函数相当于势能,在数千个维度上最小化损失函数与最大化一个演化物种的适应性是同一个问题。
乍一看,人们可能认为深度学习注定要失败。从微积分学习对最早阶段开始,我们就知道,只要有足够多的可调参数,就可以拟合任何东西,但拟合是没有意义的,因为它无法预测。深度学习似乎是个最糟糕的例子。当优化空间的维度比建模系统的自由度大几个数量级时,拟合数千个可调参数怎么可能有用?
答案来自于高维几何学。高维度上中性网络的普遍存在,留出了很多机会来逃开局部最小值。事实上,局部最小值在高维度上很罕见,当它们出现时,附近就有一个中性网络,可以逃到上面去(如果学习过程的有效温度设置得足够高)。因此,尽管可调参数的数量大得离谱,但作为与梯度下降相结合的部分策略,通过增加围绕目标景观的随机游走,可以找到有意义的、可预测的一般解决方案。
鉴于深度学习与人类思维的肤浅类比,超高维度的随机游走几何学可能部分解释了我们自身潜在的智能和意识。
S. Gravilet, Fitness Landscapes and the Origins of Species. Princeton University Press, 2004.
M. Kimura, The Neutral Theory of Molecular Evolution. Cambridge University Press, 1968.
https://galileo-unbound.blog/2021/06/28/a-random-walk-in-10-dimensions/
跨尺度、跨层次的涌现是复杂系统研究的关键问题,生命起源和意识起源这两座仰之弥高的大山是其代表。而因果涌现理论、机器学习重整化技术、自指动力学等近年来新兴的理论与工具,有望破解复杂系统的涌现规律。同时,新兴的因果表示学习、量子因果等领域也将为因果涌现研究注入新鲜血液。
集智俱乐部特别组织「因果涌现」系列读书会,深入研读相关文献,激发科研灵感。目前已经进行了两季,聚集了500+成员,积累了大量论文解读资料。欢迎感兴趣的朋友报名,加入因果涌现社区,并解锁对应录播权限。
读书会详情与报名方式请参考:
因果涌现读书会启动:连接因果、涌现与自指——跨尺度动力学与因果规律的探索
因果、涌现与机器学习:因果涌现读书会第二季启动