PRL速递：反常动态标度确定普适临界奇异性

关键词：临界相变，反常扩散，标度律，罕见事件统计

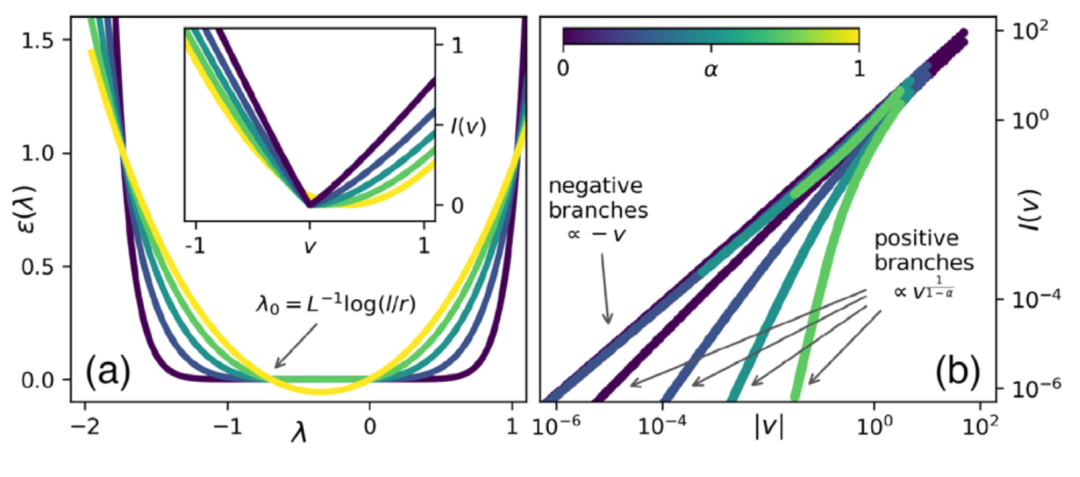
论文题目：Anomalous Dynamical Scaling Determines Universal Critical Singularities

论文来源：Physical Review Letters

论文链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.130.207104

标度律是我们理解临界平衡系统和与二阶相变相关的奇异现象的基础。在这一背景下，观察指标的概率密度函数（PDF）的比例发挥了关键作用，如自排斥聚合物在不同主链长度下的空间跨度，或不同系统尺寸的有限伊辛模型的磁化。

反常扩散现象发生在从细胞内到天体物理范围的长度尺度上。这篇文章表明扩散系统的标度特性意味着标度函数衰减的特定形式，它决定了位移的标度累积量生成函数中的标度奇异性。值得注意的是，作者表明这种奇异性源自曾经为伊辛系统的磁化假设的标度函数的相同形式的衰减，包括调制标度因子。奇异性传播到大偏差函数并导致动力学响应函数发散，类似于平衡时的磁化率。Fisher 关系显示为遵循累积量生成器的时间广度特性。平衡和非平衡问题的这种关系的普遍性源于它与大偏差特性的明确联系。

这项研究还解决了偏向扩散的情况，获得与平衡系统中没有类似物的标度形式相对应的奇点。所有这些都通过连续时间随机游走的精确计算，和相关的分数漂移扩散方程作为异常扩散的通用模型得到验证。通过这种方式，这项研究在统计力学的三大支柱之间建立了桥梁：标度、反常扩散和大偏差理论。