PRL 速递:距离控制的随机游走

关键词:随机游走,非马尔科夫过程,临界值

论文题目:Range-Controlled Random Walks 论文来源:Physical Review Letters 论文链接:https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.130.227101
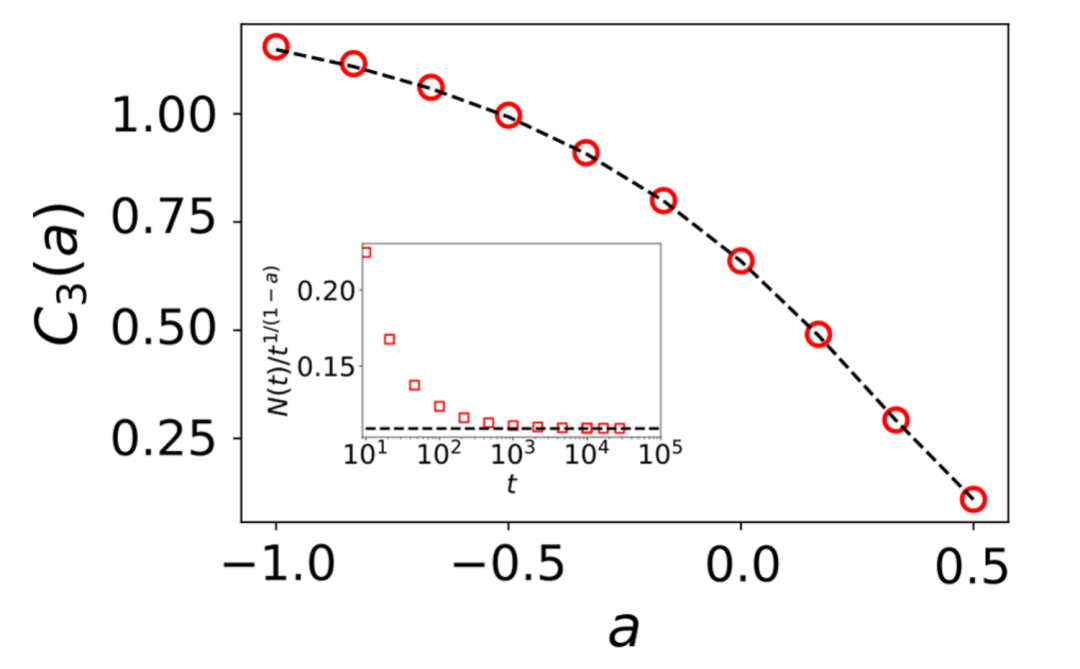
图2:由模型得出的系数C3(a)(黑色虚线)与数值模拟结果的比较。
复杂科学最新论文

推荐阅读

关键词:随机游走,非马尔科夫过程,临界值


论文题目:Range-Controlled Random Walks 论文来源:Physical Review Letters 论文链接:https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.130.227101


图2:由模型得出的系数C3(a)(黑色虚线)与数值模拟结果的比较。

复杂科学最新论文

推荐阅读