论贝叶斯力学:关于信念的物理学
关键词:贝叶斯力学,自组织,复杂适应系统,概率分布空间,信念空间,自由能原理


论文题目: On Bayesian mechanics: a physics of and by beliefs 论文地址: https://royalsocietypublishing.org/doi/10.1098/rsfs.2022.0029
贝叶斯力学(Bayesian mechanics,mechanic指机制,译为力学)是近十年来新兴的研究领域,源于贝叶斯概率,被认为有望推动发现自组织和复杂适应系统的普遍机制。它是一种概率力学,提供了一套工具,使我们能够对具有特定分区(即粒子)的系统进行建模,其中特定系统的内部状态(或内部状态的轨迹)编码关于外部状态的信念参数(parameters of belief)。这与经典力学的主要区别在于,贝叶斯力学使用概率来描述系统,而经典力学则依赖于牛顿定律和微分方程来描述系统。
在贝叶斯概率中,我们可以将概率视为对某个命题的信念程度。这种信念程度可以通过贝叶斯定理进行更新,从而反映新出现的证据。贝叶斯概率是一种主观概率,因为它反映了个体的信念,而不是事件发生的频率。在贝叶斯力学中,“信念”是指对外部状态(或其轨迹)的参数化概率分布。这些分布可以通过观察到的数据进行更新,因此它们可以被视为对外部世界的“信念”。我们可以将物理系统视为在信念空间中移动的点,这些点遵循一组微分方程,描述了信念如何随时间演化。因此贝叶斯力学的研究工具,允许我们为看似后验概率分布的复杂系统构建理论。这为建模此类系统动态的约束、力、势和其他量提供了可靠方法,特别是当它们涉及到信念空间(即统计流形)上的动力学时。
在这篇研究中,Maxwell Ramstead等人讨论了动力学、力学和场论等之间的关系。然后,作者深入讨论了贝叶斯力学的现状,并在规范场论方面引入了自由能原理(FEP, free energy principle),在自由能原理的基础物理学和动力系统观点之间架起了桥梁。通过全面回顾自由能原理的研究,作者区分了其在贝叶斯力学中的三种主要应用方式,即路径跟踪、模式跟踪和模式匹配。作者试图基于贝叶斯力学创建一个通用的系统理论,使其能够在一个正式的建模框架内描述所有的“事物”。
自由能原理是重要的数理基础,其核心原则是如果某物在一段时间内保持一定的结构,那么它必须编码或实例化其环境的统计(生成)模型。换句话说,自由能原理告诉我们,那些在嵌入环境中保持其结构的事物必然获得了该环境的统计结构。我们可以利用自由能原理为定义在特定方式的“事物”或“粒子”编写力学理论。
从一个系统的特定划分模型开始,其中系统内部状态的轨迹编码了关于外部状态/过程的信念参数,自由能原理的核心原则是从最大熵原理(the principle of maximum entropy)中重新推导出来的,两者之间具有对偶性。最大熵原理提供了从外部观察者的视角来看待问题的方法,这个视角关注的是系统如何维持其结构,防止其在一定的时间尺度内消散到环境中。自由能原理与最大熵原理的二元对偶(这是一种对称),为复杂系统研究照亮了一条路径:允许系统地研究远离平衡态并逃避稳态密度或静态统计的系统。该研究被称为G理论,它结合了对称性和涌现的概念。
作者讨论了在这个框架中,如何确定那些,“看似”是在所有的感知状态原因中估计后验概率分布的系统的力学理论。在不同类别的模型中建立交互系统的“推理动力学”,这些模型被描述为路径跟踪、模式跟踪和模式匹配。然后,作者利用最大熵的描述,对这些推理动力学进行了规范场论描述。虽然这种关于复杂性和相互作用系统的新观点可能会引发争论,但创建这样一个正式的建模框架具有重大的意义。与这个问题最相关的是它的跨学科性:在这些异质的知识领域中提供一个统一的主题,提供了产生新见解的机会,以及实现这些见解的方法。
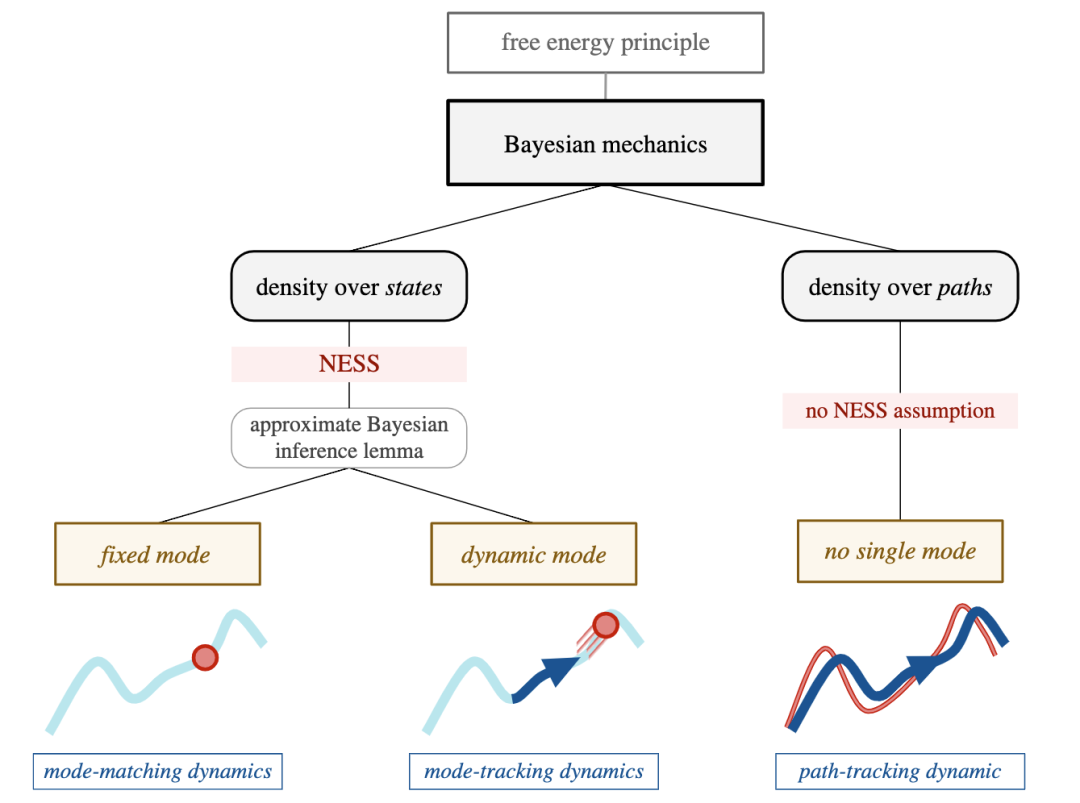
图1:自由能原理与贝叶斯力学的三个主要方面。
图1展示了贝叶斯力学的三个主要方面,它们都是基于自由能原理的应用。这三个方面可以被视为一棵树,有两个分支点。
路径跟踪(Path-Tracking):这是基于自由能原理的路径或轨迹密度的应用。这种方法关注的是特定系统的路径或轨迹的变化。
模式跟踪(Mode-Tracking):这是基于自由能原理的状态密度的应用,这种方法依赖于系统力学的非平衡稳态解。模式跟踪关注的是系统的动态模式。
模式匹配(Mode-Matching):这也是基于自由能原理的状态密度的应用,但是这种方法应用于具有静态模式的系统。
复杂科学最新论文

推荐阅读










