导语


复杂的生命如何从化学中产生？生命和非生命的界线如何确定？如果遇到具有不同化学组成的外星生命，我们能识别出来吗？英国格拉斯哥大学的 Lee Cronin 和美国亚利桑那州立大学的 Sara Walker 领导的研究小组，提出一种称为组装理论（assembly theory）的方法，通过计算从构造模块组成物体需要的最少步骤，来客观地衡量物体的复杂性。组装理论可以在生物与非生物分子之间划出一条明确的分界线，并可能为复杂性的产生和演化带来全新视角。


现任北京师范大学珠海校区-复杂系统国际科学中心特聘副研究员的刘宇博士长期专注生命起源和信息理论的研究，他对组装理论进行了评论，梳理了历史上的多种复杂度理论，指出组装理论可能存在的疑难之处，并介绍了另一种刻画复杂度的理论——梯径（Ladderpath）理论。


关键词：生命起源，生命复杂性，复杂性度量，组装理论，信息论

Philip Ball | 作者

郭瑞东 | 译者

梁金 | 审校


 



1. 思考复杂性的新视角




其他世界的生命，如果存在的话，可能如此陌生以至于难以辨认。我们无法保证外星生物会使用与地球上一样的化学物质，比如 DNA 和蛋白质这些熟悉的构建模块。科学家甚至可能观察到这些生命形式的迹象，但不知道它们是生物体。
 
这个问题远非假设性的。今年四月，欧洲航天局的 Juice （木星冰卫星探测器，Jupiter Icy Moons Explorer）航天器从法属圭亚那发射升空，飞往木星及其卫星。木星的其中一颗卫星，木卫二，在其冰冻外壳下有一片深邃的海洋，是太阳系中最有希望寻找外星生命的地方之一。
 
明年，美国宇航局（NASA）的木卫二快船飞船将发射，目标同样是探访木卫二。两艘航天器都配备了机载仪器，将寻找复杂有机分子的指纹ーー这可能是冰下生命的迹象。2027年，NASA 计划发射一架名为“蜻蜓”的无人驾驶直升机，飞越土星卫星泰坦的表面。泰坦是一个雾蒙蒙、碳含量丰富的世界，拥有液态碳氢化合物湖泊，可能正适合孕育生命——但并非我们所知的形式。
 
自从20世纪70年代科学家们第一次尝试用维京号登陆器寻找火星生物的迹象以来，有一个障碍一直困扰着科学家：没有生命的确切信号。最近的任务以及即将展开的其他任务将面临同样的障碍。不过这种情况正在发生改变。
 
2021年，苏格兰格拉斯哥大学的 Lee Cronin 和美国亚利桑那州立大学的 Sara Walker 领导的研究小组，提出了一种通用方法来识别生命系统产生的分子——即使这些分子使用的是不熟悉的化学物质。他们的方法假设，外星生命形式会产生与地球生命具有相似化学复杂度的分子。
 
论文题目：
Identifying molecules as biosignatures with assembly theory and mass spectrometry
论文地址：
https://www.nature.com/articles/s41467-021-23258-x
 
他们提出的理论被称为组装理论（assembly theory），其背后的想法目标甚至更加宏大。正如在最近的一系列论文中所展示的，它试图解释，像你我这样明显不可能存在的事物，为何能够存在。它寻求解释的方式，不是以通常的物理学方式，构建永恒的物理定律，而是通过一个过程，将生命成为生命之前的历史和记忆注入物体中。组装理论甚至试图回答一个困扰科学家和哲学家几千年的问题：生命究竟是什么？

论文题目：
Exploring the sequence space of unknown oligomers and polymers
论文地址：
https://www.sciencedirect.com/science/article/pii/S2666386421004100

论文题目：
Exploring and mapping chemical space with molecular assembly trees
论文地址：
https://www.science.org/doi/10.1126/sciadv.abj2465
 
毫不奇怪，这样一个雄心勃勃的项目引发了质疑。它的支持者尚未明确指出如何在实验室对理论进行测试。一些科学家想知道，组装理论是否能够实现其更为温和的承诺，区分生命和非生命，并以一种新的方式思考复杂性。
 
但其他人认为，组装理论方兴未艾，它可能真的为复杂性如何产生和演化这一问题带来全新视角。演化理论学者、圣塔菲研究所主席 David Krakauer 表示，组装理论提供了一种发现事物的可能历史的方法，这个问题被大多数复杂性理论所忽视。这些理论往往只关注事物是什么样，而不关注它们是如何变成那样的。亚利桑那州立大学的物理学家 Paul Davies 表示赞同，称之为“一个有可能改变我们思考复杂性方式的新想法。”
 

图1. 组装理论试图捕捉 Lee Cronin 的直觉，即复杂分子不可能凭空产生，因为组合空间太大了。Lee Cronin 的学者主页：https://www.chem.gla.ac.uk/cronin/

 
 



2. 事物的顺序




组装理论的灵感来自于当 Cronin 问道，组合不同原子的方式如此之多，为什么大自然会产生一些分子，而不是其他分子。根据物理学定律，说一个物体可能存在，这是一回事；从组成部分实际构造出物体，又是另一回事。Cronin 说: “组装理论捕捉的是我的直觉，即复杂分子不可能凭空出现，因为组合空间太大了。”
 
与此同时，Walker 一直在努力探索生命起源问题——这个问题与制造复杂分子密切相关，因为生物体内的分子过于复杂，不可能是偶然组装起来的。Walker 若有所思地说，在达尔文自然选择理论接管之前，一定有什么东西引导了这个过程。
 
Cronin 和 Walker 在2012年参加了 NASA 的一个天体生物学研讨会后，进入了这个研究课题。Cronin 回忆说：“Sara 和我当时在讨论信息论和生命，以及建造自复制机器的最小路线。我们都清楚地认识到，在生物出现之前，缺少一种‘驱动力’。”
 
两人现在认为，对于复杂物体如何产生这一显而易见的历史偶然性，组装理论提供了一个自洽的、数学上精确的的解释——例如，火箭不会凭空产生，首先得出现多细胞生命，然后才会有人类，再然后出现文明和科学，在此基础上才可能建造火箭。事物的出现有一个特定的顺序。
 
Walker 说：“我们生活在一个递归结构的宇宙中。大多数结构必须建立在对过去的记忆之上。信息随着时间积累。”
 
这在直觉上似乎是显而易见的，但是关于事物顺序的一些问题却更难回答。恐龙必须先于鸟类吗？莫扎特必须先于 John Coltrane（美国爵士乐演奏者） 吗？我们能说哪些分子必然先于 DNA 和蛋白质吗？
 

图2. 美国亚利桑那州立大学的 Sara Walker 一直在探索地球生命的起源，以及如何识别遥远星球的其他生命形式。Sara Walker 的学者主页：https://search.asu.edu/profile/1731899

 
 



3. 量化复杂性




组装理论提出了一个看似没有争议的假设，即复杂的物体由许多简单的物体组合而成。该理论认为，可以通过考虑物体如何形成，来客观地衡量物体的复杂性。这可以通过计算从成分组成一个物体需要的最少步骤，量化为组装指数（Assemble Index, AI）。
 
一个从科学角度而言有趣的复杂物体，必然有很高的组装指数。非常复杂的事物可以从随机组装过程中产生——例如，你可以通过将任何已有的氨基酸连接成链来制造类似蛋白质的分子。然而，一般来说，这些随机分子不会有什么有趣的性质，比如像酶一样执行催化工作。而且用这种方法得到两个完全相同分子的可能性微乎其微。
 
然而，在生物体中，功能性酶一次又一次被可靠地制造出来，因为它们不是随机组装的，而是来自于跨代遗传的基因指令。因此，虽然找到一个单一的、高度复杂的分子并不能让你知道它是如何形成的，但是找到许多相同的复杂分子是非常不可能的，除非某种精心安排的过程——也许是生命——在起作用。
 
Cronin 和 Walker 认为，如果一种分子的丰度足够高，可以被检测到，那么其组装指数可以表明，它是否由一个有机的类生命过程产生。这种方法的吸引力在于，关于分子本身或制造它的类生命实体的化学细节，没有做任何假设。它忽略化学细节。这使得在寻找可能不符合地球生物化学的生命形式时，组装理论显得尤其有价值，康奈尔大学行星科学家 Jonathan Lunine 说道，他也是在土星冰冷的卫星土卫二上寻找生命计划的首席研究员。
 
Lunine 说：“至少有一种相对不可知的技术需要在生命探测任务中使用。”他补充说，利用已经用于研究行星表面化学的技术，有可能实施组装理论所要求的观测，从而确认使用组装理论解释数据是可行的。
 
 



4. 衡量生命复杂性的指标




我们需要的是一种快速简便的实验方法来确定特定分子的组装指数。利用化学结构数据库，Cronin、Walker 和他们的同事设计了一种方法来计算制造不同分子结构所需的最小步骤数。他们的结果表明，对于相对较小的分子，组装指数大致与分子量成正比。但是对于较大的分子（比如比小肽更大的分子），这种关系就不成立了。
 
在这些情况下，研究人员可以利用质谱法（mass spectrometry）来估算组装指数。NASA 的“好奇号”探测器已经使用这项技术来识别火星表面的化合物，NASA 的“卡西尼”号航天器也使用这项技术来研究从土卫二喷发出来的分子。
 
质谱法通常会将大分子分解成碎片。Cronin、Walker及其同事发现，在这个过程中，高组装指数的大分子比低组装指数的大分子（例如简单重复的聚合物）会分裂成更复杂的碎片混合物。通过这种方式，研究人员可以根据分子质谱的复杂性可靠地确定组装指数。
 
当研究人员随后测试这项技术时，他们发现由生命系统产生的复杂分子混合物——大肠杆菌培养物、紫杉醇（太平洋红豆杉的代谢物，具有抗癌特性）、啤酒和酵母细胞等天然产物——通常比矿物质或简单有机物的平均组装指数要高得多。
 
这种分析很容易出现假阴性——一些生命系统的产物，如阿德贝格单一麦芽苏格兰威士忌，有更低的组装指数，显示来自非生命系统。但也许更重要的是，实验没有产生假阳性：非生物系统不可能有足够高的组装指数来冒充生物体。因此，研究人员得出结论，如果在另一个世界测量得到具有高组装指数的分子样本，它可能由我们称之为生命的实体所制造。
 

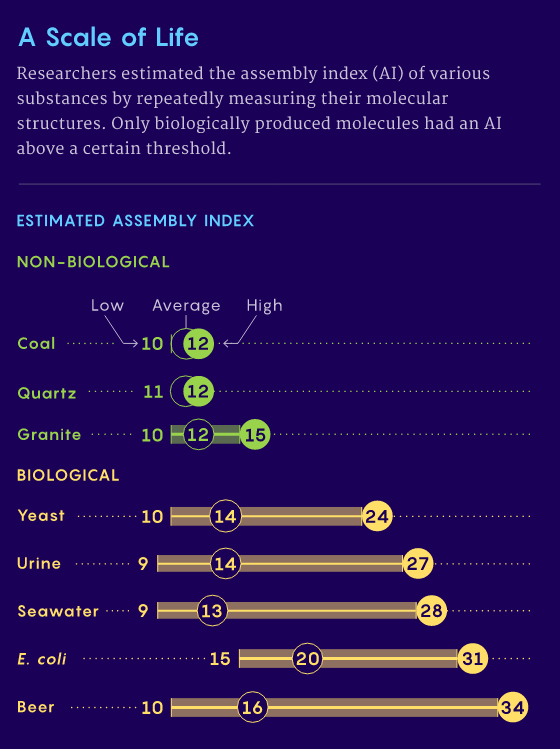
图3. 研究人员通过反复测量分子结构来估计不同物质的组装指数，非生物与生物分子之间存在明确的分界。| 来源：https://www.nature.com/articles/s41467-021-23258-x

 
质谱法只能用于天体生物学搜索，需要接触物理样本，也就是登陆任务，或者像欧洲航天局的木卫二探测器这样的轨道飞行器，可以接收和分析从星球表面喷射出来的分子。但是 Cronin 和同事们最近的研究证明，他们可以使用其他两种技术测量分子的组装指数，并得到一致的结果。其中一种是红外光谱学，可以用例如韦伯空间望远镜上的仪器，远距离探测遥远世界的化学组成。
 
论文题目：
Multimodal Techniques for Detecting Alien Life using Assembly Theory and Spectroscopy
论文地址：
https://arxiv.org/abs/2302.13753
 
这并不是说，这些分子检测方法提供了一个干净的观测指标，可以区分从岩石到爬行动物。剑桥大学计算机科学家和生物技术学家 Hector Zenil 指出，格拉斯哥研究小组检测的所有样本中，组装指数最高的物质——根据这种衡量标准可能被认为最具“生物特性”的——不是细菌，而是啤酒。
 

图4. Hector Zenil，剑桥大学计算机科学家和生物技术学家，算法信息动力学提出者。学者主页：https://hectorzenil.net/

 
 



5. 挣脱决定论的枷锁





组装理论预言，像我们这样的生命体不可能孤立地出现——一些复杂的物体只能与其他物体一起出现。这在直觉上是有道理的，宇宙不可能只生产一个人。要产生人类，必然会产生一大群人。
 
对于像人类这样“泛称”的具体实体（以及你我这样的特例），传统物理学能给出的解释有限。物理学提供了自然法则，并假定特定的结果来自于特定的初始条件。按照这种观点，我们一定在宇宙诞生的最初时刻就以某种方式被编码好了。但这肯定需要极端精细调节的初始条件，使智人（更不用说你）的出现不可避免。
 
组装理论可以摆脱这种过度确定的图景。在这里，初始条件并不重要。相反，制造像我们这样的特定物体所需要的信息在一开始并不存在，而是在宇宙演化的展开过程中积累起来的——这样我们就不必将所有责任归结到几乎不可能经过精细调节的宇宙大爆炸。Walker 说，信息“在过程中，而不是在初始条件。”
 
除了 Cronin 和 Walker，还有其他科学家试图解释，为何观测现实的关键并不在宇宙法则，而在于某些物体的组装或变换方式。牛津大学的理论物理学家 Chiara Marletto 和物理学家 David Deutsch 正在发展类似的想法。他们将自己的方法称为构造函数理论（constructor theory），该理论考虑哪些类型的变换是可能的，哪些是不可能的，Marletto 认为其“在精神上接近”组装理论。（参看《物理学家改写导致无序的基本定律》）
 
Cronin说：“构造函数理论讨论的是能够进行特定变换的任务的集合。它限制满足物理定律的情况下可能发生的事情。”而组装理论为这个等式增加了时间和历史。为了解释为什么有些物体能够被制造出来，而有些却不能，组装理论确定了一个包含四个不同“宇宙”（universe）的嵌套层级结构。
 
在组装宇宙（Assembly Universe）中，基本构造模块的所有排列都是允许的。在可能组装宇宙（Assembly Possible）中，物理定律对这些组合施加约束，因此只有一些物体是可行的。然后，偶然组装宇宙（Assembly Contingent）通过挑选那些实际上可以沿可能路径组装的物体，对物理上允许的大量物体进行削减。第四个宇宙是观测组装宇宙（Assembly Observed），它只包括那些生成我们实际看到的特定对象的组装过程。
 

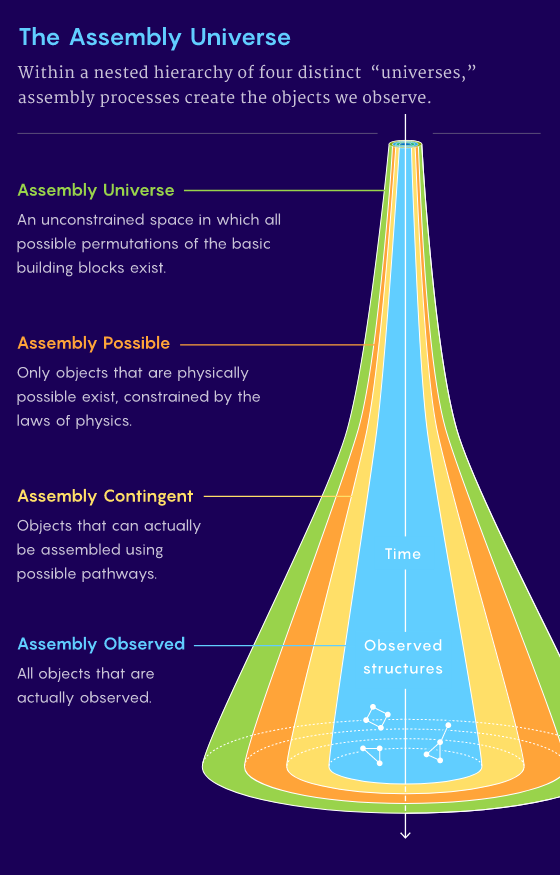
图5. 组装宇宙四个层级的示意图。组装理论确定了包含四个不同“宇宙”的嵌套层级结构，组装过程创造了我们观察到的物体。

 
论文题目：
Assembly Theory Explains and Quantifies the Emergence of Selection and Evolution
论文地址：
https://arxiv.org/abs/2206.02279
 
组装理论探索所有这些宇宙的结构，使用的想法来自对图或相互连接的节点网络的数学研究。Walker 说，这是一种“对象优先的理论，组装理论关注的是实际制造出来的物体，而不是它们的组成部分。”
 
论文题目：
Formalising the Pathways to Life Using Assembly Spaces
论文地址：
https://www.mdpi.com/1099-4300/24/7/884
 
为了理解组装过程如何在这些概念宇宙中运作，可以考虑达尔文演化理论的问题。按照惯例，演化是一旦复制分子随机出现就“立即发生”的事情——这种观点可能有同义反复的风险，因为它似乎说演化是在可演化的分子存在之后开始的。Marletto 说，相反，构造理论和组装理论的拥护者正在寻求“植根于物理学的对演化论的定量理解”。
 
根据组装理论，在达尔文演化论发挥作用之前，必须从组装可能宇宙中选择高组装指数对象的多个副本。Cronin 说，单单化学过程就可能做到这一点——把相对复杂的分子缩小到较小的子集。普通化学反应已经在所有可能排列中“选择”了某些产物，因为它们有更快的反应速度。
 
前生命环境中的特定条件，如温度或催化矿物表面，因此可能已经开始在组装可能性宇宙中筛选构成生命的分子前体池。根据组装理论，这些前生命环境偏好将被今天的生物分子记住：这些分子编码了自己的历史。一旦达尔文的自然选择理论接管，它会倾向选择那些能够更好地自我复制的物体。在这个过程中，这种对历史的编码变得更加强烈。这就是为什么科学家可以利用蛋白质和 DNA 的分子结构来推断生物体的演化关系。
 
因此，组装理论“提供了一个跨越物理学和生物学的统一框架来描述自然选择，”Cronin、Walker 及其同事写道。“一个物体被‘组装’的步骤越多，就需要经历越多的自然选择才可能出现。”Cronin 说：“我们正尝试建立一个严谨的、经验可验证的理论，来解释生命如何从化学中产生。”
 
 



6. 超越所有度量方法？




Krakauer 认为，组装理论和构造函数理论都为思考复杂物体如何形成提供了新思路。“这些理论更像是望远镜而不是化学实验室。它们让我们看见事物，而不是制造事物。这不是一件坏事，而且可能非常强大。”但他警告说，“就像所有科学一样，只有亲自尝试之后才能够判定是否成功。”
 
Zenil 认为，鉴于复杂性的度量指标已经相当多，如柯氏复杂度（Kolmogorov complexity）等，组装理论只是重造轮子。对此 Marletto 不同意。她说：“复杂性有几种度量标准，每一种都捕捉到复杂性的不同概念。”但她说，这些度量标准中的大多数与现实世界过程无关。例如，柯氏复杂度假设，存在一种装置可以把物理定律允许的任何东西组合在一起。这种度量适合于“可能组装宇宙”的度量，但不一定适合“观测组装宇宙”。相比之下，组装理论是“一种有前景的方法，因为它侧重于操作定义的物理属性，而不是抽象的复杂性概念。”
 
Cronin 说，以前这些复杂性度量方法缺少的，是对复杂物体历史的了解——这些度量方法无法区分酶和随机多肽。
 
Cronin 和 Walker 希望，组装理论最终能够解决物理学中广泛的问题，比如时间的本质，和热力学第二定律的起源。但这些目标仍然遥远。“组装理论程序仍处于初级阶段，”Marletto 说。她希望看到这个理论在实验室中得到验证，但这也可能发生在对外星世界发生的类生命过程的探寻中。
 
原文链接：https://www.quantamagazine.org/a-new-theory-for-the-assembly-of-life-in-the-universe-20230504/

致谢：感谢傅渥成博士推荐文章以及提供的专业修改意见。



评论


刘宇 | 作者

 




1. 组装理论：评论




组装理论（Assembly Theory）的出发点是：如果一个体系中有大量相同的复杂分子，那么可以判断，这个体系一定是生命或类生命、或是由它们产生的。


1. “大量”这个观点是新颖的。只有单个复杂分子是不足以做出上述判断的，因为这个复杂分子完全可能是随机过程产生的。


2. 对于“复杂”这一点，即如何衡量一个分子到底有多复杂，组装理论提出了一个称为 Assembly Index 的指标，即生成该分子的最少步骤数，亦即最短路径的长度。这其实跟柯式复杂度（Komologrov Complexity）是一脉相承的；一个客体的柯式复杂度定义为，描述该客体的最短程序的长度。


Box 1.



这里有必要把与柯式复杂度有同样精神（in the same sprit）的描述客体复杂度的理论列举一下（这类理论非常多，所以以下并不能包含所有）：

1.霍夫曼编码（Huffman coding, 1952）David A. Huffman：无损数据压缩算法，根据预测到的符号重复出现的频率来编码（构造 Huffman Tree 使得任一符号都可以高效地唯一解码），频率越高，编码该符号的长度越短。

2.Lempel-Ziv 压缩算法（1976）：无损数据压缩算法，是基于字典的编码器（而不是基于如霍夫曼编码所采用的频率）；在构造字典的时候，是基于“前面出现过的亚序列可以直接重复利用”的思想。

3.“自然是修修补补的（Nature is Tinkering）”思想（1977）François Jacob（1965年诺贝尔医学奖得主）：在进化中，通常是以加入新单元或增加新功能的方式将原构件作出修改，从而产生更复杂的系统。

4. Addition Chain：历史悠久不易追溯，最著名的介绍是由 Donald Knuth（高德纳，Tex发明者）1997年在他的书中作出的；对于任意整数n，有一个最短的从1开始的整数序列，其后一项等于该序列前面的某两项之和（可用于简化幂计算，也是基于“前面出现过的就不用再计算”的思想），比如31的 addition chain 是1, 2, 3, 6, 12, 24, 30, 31。

5. 逻辑深度（1988）Charles Bennett：跟柯式复杂度很相关，但它指的是，描述该客体的最短程序运行完毕所需要的时间步数，更强调计算复杂度。

6.“可及邻域”（The Adjacent Possible, 1996）Stuart Kauffman（考夫曼）：各种各样的可能性会持续地在现有的情况下出现，当现有的可能性被开发完之后（或同时），新的可能性会持续地涌现出来。

柯式复杂度中，对于一个毫无规律（即某种意义上来说随机的）的序列，其柯式复杂度是最高的，因为对随机序列的最短描述也只能是原封不动地将原序列描述出来；组装理论将 Assembly Index 作为“复杂度”的指标，而完全随机序列的Assembly Index 是最高的，所以组装理论也会认为随机序列的复杂度最高。


但直觉上，我们并不会认为最随机的序列是最复杂的，或者说，从演化的意义上来讲，我们不会认为毫无规律的遗传序列是最复杂的，含有最多的“演化信息”。所以，组装理论和柯式复杂度面临着同样的问题（可能不能说是问题，而是特性），即最随机的、最无规律的序列是“复杂度”最高的。


我想这就是为什么牛津大学的 Hector Zenil 教授说组装理论是在重复发明轮子（Reinventing the Wheel）、跟霍夫曼编码（Huffman coding）等工作很像，并不是毫无道理；在跟生命相关的研究中，结构模块化和从基本构件开始的迭代重构这种观念有着悠久传统[1]。但我认为把这种复杂度推广到化学分子、然后在实验上把它与串联质谱法（Tandem Mass Spectrometry）的测量对应起来、用于探测“外星”未知生命，确实是新颖和大胆之处。不过，虽然做法是新颖和大胆的，但其合理性也是值得探讨的（后文会具体谈到），Zenil 教授也专门撰文说 Cronin 教授团队的实验和论断（claim）是不正确和被夸大了的[1]。

[1] Zenil et al. On the Salient Limitations of the Methods of Assembly Theory and their Classification of Molecular Biosignatures, arXiv, https://arxiv.org/abs/2210.00901 , 有4个版本，最新版是2023.4.3


Cronin教授团队将组装理论用于探测未知生命的逻辑和具体做法是：（1）对于已知的分子，首先在理论上计算 Assembly Index，然后用串联质谱法测量该分子，数出质谱上有多少个峰，将 Assembly Index 和峰的个数对应起来；（2）对大量已知分子如此操作之后，就能拟合出一条曲线，即通过串联质谱的峰的个数推测未知分子的 Assembly Index；（3）对含有生命的样品（比如海水、酵母、多肽）和非生命的样品（比如石英、石灰岩、Miller-Urey实验产物）测量后，发现含有生命的样品的串联质谱所推测出的 Assembly Index 一般都高于一个阈值，非生命的样品其 Assembly Index 较低；（4）所以，如果一个未知样本用串联质谱法测量然后所推测出的 Assembly Index 高于某个阈值，则可以判断其是生命或与生命过程有关。


不过这里面有几个疑难点：
1. 虽然组装理论定义Assembly Index为生成分子的最少步骤数，但文章中计算Assembly Index用的是一个称为split-branch的算法，本质上是在迭代地数重复亚分子结构的个数，并不能给出“生成分子的最少步骤数”。

2. 串联质谱中峰的个数是否真的与“生成分子的最少步骤数”存在确定的、鲁棒的关系，并没有给出严格说明；用split-branch给出的结果与串联质谱的拟合，来推测“生成分子的最少步骤数”就显得更加缺乏坚实基础。


Zenil 教授也通过实验指出：用传统的一维 Run Length Encoding（RLE）、霍夫曼编码等方法得出的相关性比 Assembly Index 高[1]，所以组装理论用 Assembly Index 来作出判断生命和非生命的论断是很有误导性的。


说完组装理论中“复杂”这一点，再说说“大量”这个观点：偶然出现一个复杂分子并不神奇，神奇的是同时出现很多相同的复杂分子。我认为“大量”这个观点是新颖的（但事实上，只有在2023.3.12最新一版的组装理论的arXiv文章里[2]，才提到一个称为“copy number”的量，用于描述某分子的数量，以前的版本对于“大量”都只是定性描述）。通过串联质谱的实测数据来推测是否“大量”复杂分子存在，巧妙地解决了“大量”这个问题（尽管上面所说的那两个疑难点仍然存在），因为质谱仪本来就只能检测到大量分子的信号，少量分子的信号也一般会被噪声淹没。

[2] Sharma et al. Assembly Theory Explains and Quantifies the Emergence of Selection and Evolution, arXiv, https://arxiv.org/abs/2206.02279 , 有3个版本，最新版是2023.3.12，最老版是2022.6.5


 



2. 梯径理论 vs. 组装理论




在与柯氏复杂度同样的精神（spirit）下（也是组装理论所遵循的spirit），我们提出了梯径（Ladderpath）理论。梯径理论中我们提出一个指标梯径度（Ladderpath-index）来刻画重构客体所用的最少步骤数（这跟柯氏复杂度、组装理论中的Assembly Index、Addition Chain、François Jacob的”Nature is Tinkering”等的精神是类似的）。


但我们认为梯径度并不能够刻画一个客体的“复杂度”，而必须和另一个指标有序度（Order-index）一并来刻画复杂度（有序度是梯径理论中定义的另一个量，定义为客体的规模减去客体的梯径度，具体请参见论文[3]、亦有中文版[4]、和简介[5]）。也就是说，我们直觉中的复杂度其实包含了两个方面，一个是梯径度，描述复现目标客体的难度，另一个是有序度，描述客体有多有序，只有当两者同时很大的时候才算复杂度高，这是我们跟组装理论的本质区别之一。

[3] Liu et al. Ladderpath Approach: How Tinkering and Reuse Increase Complexity and Information, Entropy, 2022 https://www.mdpi.com/1099-4300/24/8/1082（最初公开版本是2022.1.19 http://www.chinaxiv.org/abs/202201.00057）

[4] 文献[3]的中文版《梯径：“修修补补”和“重复利用”如何增加复杂度与信息》 https://zh.wuyichen.org/chinese-version-ladderpath

[5] “三刀研学室”关于《梯径理论简介》的公众号文章 


虽然上述的诸多关于复杂度的理论都提及最短路径、最少构造等（包括梯径理论、组装理论和Box 1中所提及的），梯径理论的关键点在于重复利用前面已经构造出的组件。所以在梯径理论中，只有重复出现过的组件才会被赋予特殊意义（我们称之为梯元Ladderon，梯元所构成的层级嵌套结构称为“梯图Laddergraph”）；而在组装理论中，所有出现过的都是重要部件，所有这些部件共同组成一个“组装空间”。


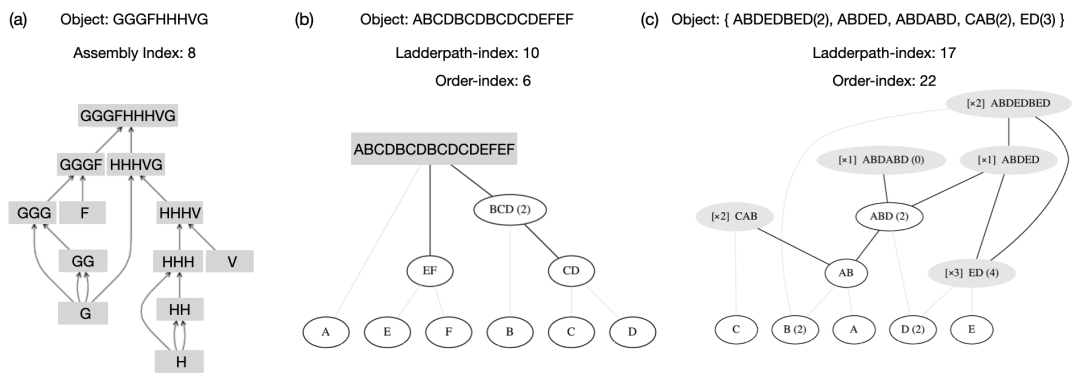
虽然梯径理论中的梯径度和组装理论中的 Assembly Index 在大的spirit上都是在描述生成目标所需的最少步骤，但它们给出的结果并不一样，见图1（更多例子请参见[6]）。此外，组装理论只强调一个客体的复杂度，而不讨论一个体系，所以一个体系的 Assembly Index 是没有定义、无法被计算的；梯径理论的着眼点是一个体系的复杂度（单个客体是在体系之下的特例），所以体系的梯径是定义良好的（well-defined）。根据所考虑的问题不同，我们还需要区分孤立体系和联合体系（比如在考虑一个中文句子的意义的时候，我们需要把它放在整个中文语境这个联合体系下考虑），详见文献[3,4]。

[6] “三刀研学室”公众号文章《Ladderpath vs. Assembly》 


图1. (a)组装理论最新的arxiv文章[2]上给出的例子：序列GGGFHHHVG的Assembly Index为8。在梯径理论中，该序列的梯径度是9程（“程”是梯径度的单位），亦即序列的长度。事实上，在梯径理论中，这个序列GGGFHHHVG是一个平庸的例子，因为它没有任何重复结构，所以它的梯径度等于它的长度，梯图中也只有最基本的单元才是它的梯元；而组装理论认为所有出现的亚结构都是重要的。(b)梯径理论文章[3,4]给出的例子：序列ABCDBCDBCDCDEFEF的梯径度为10程，有序度为6程。组装理论可能会给出其Assembly Index为9（无法验证，因为上述文献[2]并没有提供程序，也没有提供严格的流程如何计算序列的Assembly Index）。(c)一组序列组成一个整体，该体系的梯径度是17，有序度是22。组装理论无法给出一个体系的Assembly Index。


梯径理论和组装理论的另一个本质的区别是：组装理论认为“选择”（或自然选择）是复杂性增加的原因；而梯径理论认为“复制”是复杂性增加的动力和根本原因，“选择”可以从“复制”中自动涌现出来。事实上，梯径理论的另一直觉和灵感来源就是生命起源研究中的自我复制理论（这也是我们长期以来的一个研究方向），包括提出“The Adjacent Possible”的Kauffman的自催化集合理论、Chemical Organization Theory、Chemoton、超循环理论等。


 



3. 组装理论的“野心和雄心”（Ambitions）




Cronin 教授团队原文[2]中说：组装理论“提供了一个跨越物理学和生物学的统一框架来描述自然选择”。但 Zenil 教授说：对于组装理论能够很好地刻画生命、甚至地外生命的能力（包括区分生命和非生命的能力），非常具有误导性、或者被严重地夸大了，使得它吸引了很多的不应得（undeserved）的媒体注意，而这对于以前或将来的研究都是不利的[1]。我们也认为声称组装理论是一种统一框架有点夸大其词了，听起来像是完全从0到1的工作，但正如 Zenil 教授所说的，这种“最短路径”逻辑有着相当长的历史，声称“框架至此统一了”并不利于这类理论的后续进一步发展。


事实上，这一大类理论一般可被称为算法信息论（Algorithmic Information Theory），其中一些分支着眼于生命系统和演化，一些着眼于计算理论等等，但大多分支都是一脉相承的，我们可以从以往诸多文献（如[1,3]等）中找到发展脉络。这些理论之间都有相互借鉴，并不完全排他。这类理论的发展似乎正好印证了François Jacob 所说的“自然界（当然也包括人类社会和科技）是修修补补的（Nature is Tinkering）”，就像这些理论描述了它们自身的演化。


 

刘宇：现任北京师范大学珠海校区-复杂系统国际科学中心特聘副研究员，独立PI。小组目前研究神经网络和基因序列的模块演化、新药分子的设计、以及关于生命起源和信息的理论研究，详见微信公众号“三刀研学室”。



自生成结构读书会


生命是有心（意识）的，但当你一层层剥开生命的组织，却只有心脏而没有一颗“心灵”；打开大脑皮层看到一个个神经元，却看不到“意识”。然而，生命与意识都具有“自我生成“的能力，生命自发从非生命中生成，意识自发从生命中生成。更惊人的是，生命与意识的自我生成结构似乎很相似。如果这个假设成立，那么最可能的备选结构会是什么呢？


为了更深入地认识复杂活系统的自生成结构，集智科学家小木球（仇玮祎）联合周理乾、王东、董达、刘宇、苑明理、傅渥成、章彦博等科学哲学、计算机科学、物理学和生物化学等学科的一线研究者共同发起组织《自生成结构系列读书会》。其中第一季《共识——自生成结构与自复制自动机的研究背景》已经完结，读书会所形成的自生成结构社群集结了相关领域的教授、硕博及产业界人士。现在报名读书会即可解锁第一季读书会所有录播视频并入群，欢迎从事相关研究、对相关领域有浓厚兴趣的探索者报名参与交流。



详情请见：
自生成结构读书会启动：剖解生命、意识与智能的核心结构


阅读原文链接：https://pattern.swarma.org/study_group/13?from=wechat



推荐阅读

1. 生命起源与复杂性 | 刘宇访谈
2. 外星生命或智能摆在面前，你能认出来吗？——“梯径”提供的思路
3. 如何发现不同分子结构之间的关系？用“分子树”探索化学空间
4. 《张江·复杂科学前沿27讲》完整上线！
5. 成为集智VIP，解锁全站课程／读书会
6. 加入集智，一起复杂！



点击“阅读原文”，报名读书会