现实世界中大量问题的解决需要设计和求解算法。传统上通常是人类学习如何设计算法,而随着人工智能技术的发展,我们也可以通过机器学习方法去学习如何设计算法。对于组合优化问题,机器学习算法能够求解超大规模的复杂系统问题,具有强大的优势。
在「图神经网络与组合优化」读书会第一期分享中,国防科技大学系统工程学院副教授范长俊介绍了机器学习求解组合优化的问题,特别是图上的组合优化问题,包括最小节点覆盖、网络瓦解、自旋玻璃基态求解问题的最新进展,并进一步探讨了一些有意思的研究进展。本文是此次读书会分享的整理。
欢迎扫码观看读书会视频回放:

https://pattern.swarma.org/study_group_issue/483?from=wechat
范长俊 | 讲者
王志鹏 | 整理
梁金 | 编辑
组合优化是通过对数学方法的研究寻找离散事件的最优编排、分组、次序或筛选,是运筹学的一个重要独立分支,是一类重要的优化问题。组合优化在现实中的应用也十分广泛,包括在拍卖设计、资源调度、生成、物流以及军事领域等都有广泛应用。此外,常见的需要组合优化来求解的经典问题包括:0-1背包问题、旅行商问题(TSP)、最小节点覆盖问题(MVC)、最小支配集问题(MDS)以及最大割问题(Max-Cut)等。
目前组合优化算法主要可以分为以下四类:
1)数学优化算法,包括分支定界、分支定价、分支切割等方法,这是一种精确算法,该方法优点是能找到全局最优解,并且能有理论保证,缺点在于时间呈指数增长,不适合求解大规模的问题;
2)启发式算法,包括近似算法、贪婪算法等,这类算法优点是存在最差解的质量保证,缺点是求解时间比较长,并且这类近似算法很难构造;
3)元启发式算法,如遗传算法、蚁群算法、模拟退火算法等,这类算法优点是比较容易实现,求解时间也不会太长,很快得到一个可行解,缺点在于该类算法对参数比较敏感,不同的实例都需要重新调整参数;
4) 机器学习方法,包括监督学习、强化学习以及图神经网络等,该类方法优点是能从同分布的数据中学习到通用的规律,能快速求解同一类问题。
总之,前三类算法可以看成是人类学习如何去设计算法,该类算法规模适中、模型相对稳定、能求解一些经典问题同时也存在理论保证,而最后一类方法是通过机器学习方法去学习如何设计组合优化算法,该类算法能求解超大规模问题,是实时变化的,能处理复杂系统,唯一的缺点是该类算法是一种弱最优性。除了上述四类优化算法以外,也存在一些组合优化的求解器,包括商用求解器,Gurobi、CPLEX等以及开源求解器,SCIP以及LP_Solve等。
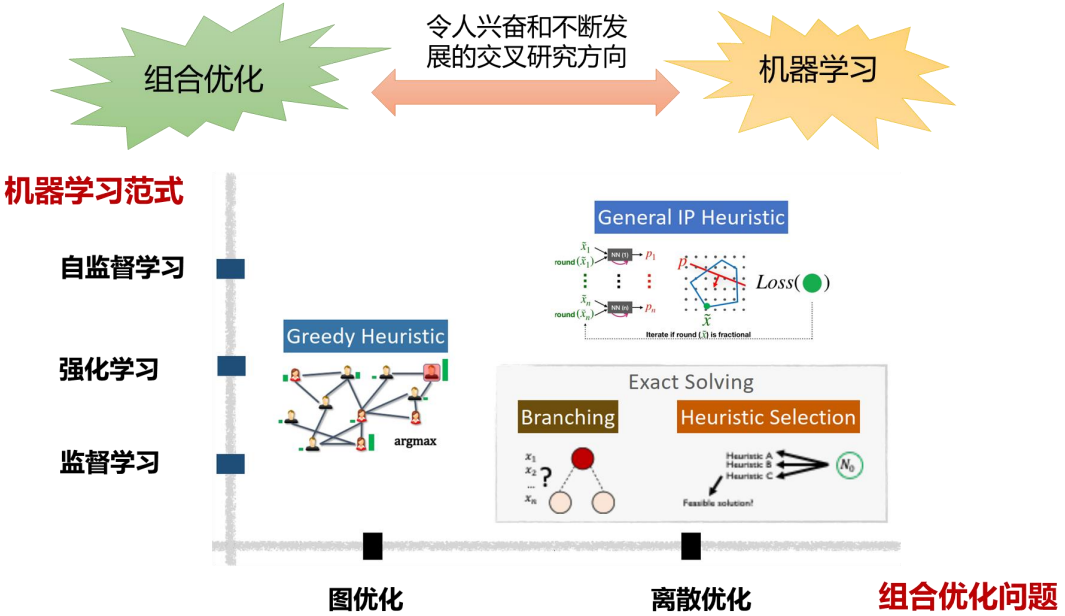
目前机器学习组合优化是人工智能的前沿方向,可以通过使用不同的机器学习方法来解决不同的组合优化问题,如图优化以及离散优化等。
目前组合优化问题的机器学习求解范式可以分为两类:
1)基于端到端求解,输入是问题的实例输出是问题的结果,使用自回归或者非自回归的方法学习一些启发式的策略;
2)局部改进求解,包括改进精确算法或者启发式算法等,将这些算法中比较耗时的模块转换成一个学习问题,从而加快求解的速度,如对于分支定界算法, 可以将传统的使用强连通量进行分支转换成一个二分类的学习问题。
图上的组合优化问题是组合优化问题中很重要的部分,很多图上的组合优化问题都是NPC问题,只要证明任意一个NPC问题存在精确的多项式算法,那么所有的NP问题就都解决了,那么P=NP。
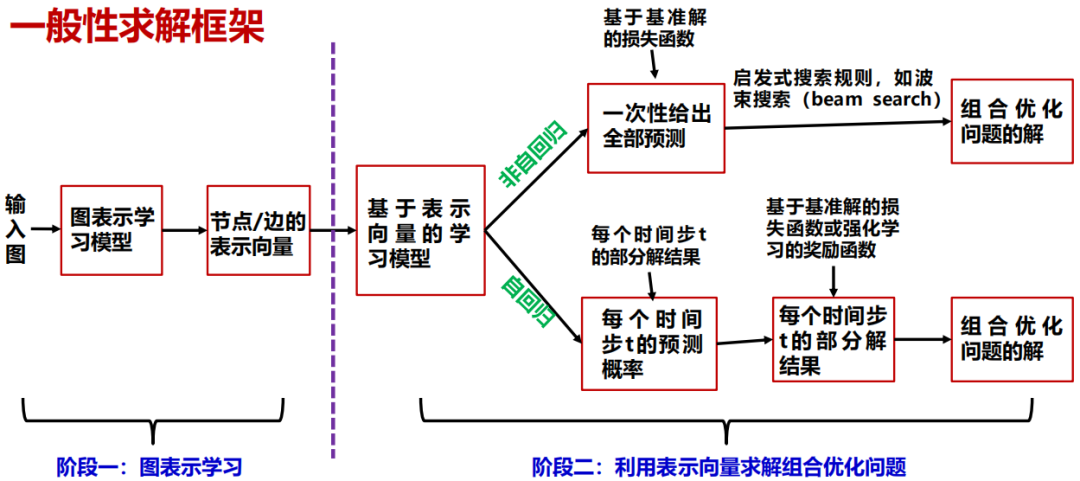
图上的组合优化问题的一般性求解框架具体分为两个阶段:第一个阶段进行图的表示学习,学习节点或边的表示向量;第二个阶段基于表示向量求解组合优化问题,可以使用非自回归方法结合启发式搜索规则,或者基于强化学习的自回归进行优化求解。下面分别具体介绍这两类方法。
Combinatorial Optimization with Graph Convolutional Networks and Guided Tree Search
https://arxiv.org/abs/1810.10659
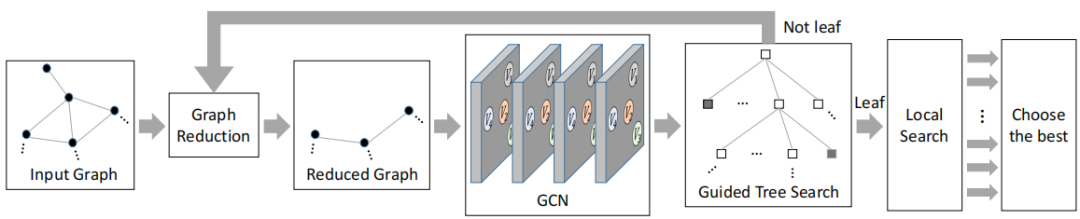
该论文尝试解决最小支配集、最小节点覆盖以及最大割这样的NPC问题,使用监督学习算法结合树搜索以及图论技巧来学习。具体来说,模型输入一个图,然后对图进行约简,将约简后的等价图输入GCN中学习每个节点选中与否的概率,然后结合树搜索算法以及图论的局部搜索算法选择最优的结果,输出图中的每个节点是否被选中。损失函数是一个交叉熵损失,表示第i个训练图的第j个节点的标签,表示GCN输出的第j个节点选中与否的概率。为了解决组合优化解不唯一的情况,作者使用 hindsight loss 优化GCN输出多个loss的最小值。其中通过后面的实验发现图论技巧对于性能的提升占了很大比重,去掉局部搜索的技巧,预测的性能显著降低。但是该类算法的缺点在于泛化效果比较差, 除非加很多领域的专业技巧才能提高性能。
图3 基于图卷积网络和引导树搜索的组合优化算法流程图
第二类为自回归算法,其框架主要就是结合图表示学习和强化学习来优化目标。下面主要介绍三个工作,S2V-DQN (NIPS 2017)、FINDER (NMI 2020) 以及 DIRAC (NC 2023)。
Khalil E, Dai H, Zhang Y, et al. Learning combinatorial optimization algorithms over graphs[J]. Advances in neural information processing systems, 2017, 30.
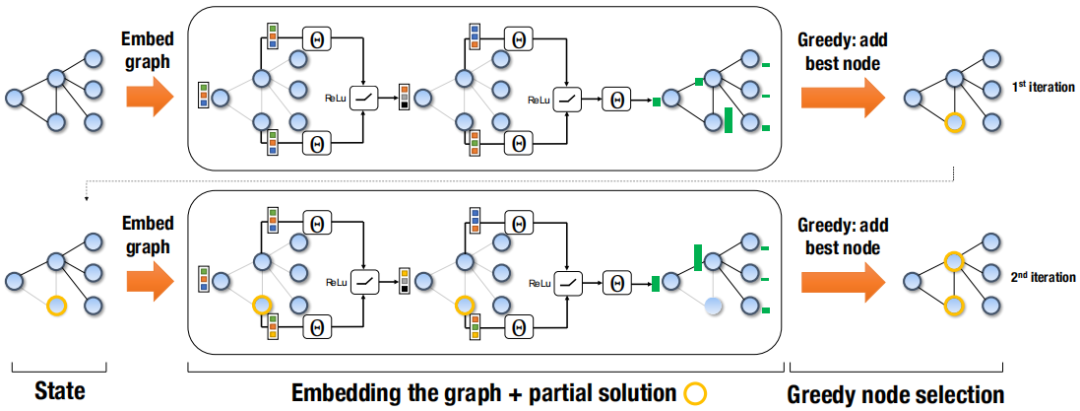
该工作是机器学习组合优化领域的里程碑式工作,引领并启发了该领域后续许多的研究。该方法的整体框架是输入一个图,然后使用多层的 Graph Embedding 方法得到每个节点的表示向量,然后通过Q-Learning算法为每个节点算一个Q-value作为节点选择的长期收益,收益最大的节点被选中,然后重复Graph Embedding和Q-Learning直到满足终止条件。其中这里的Graph Embedding使用Struct2Vector算法。
算法训练过程主要包括四个部分:1)生成训练图数据;2)探索和利用选择节点;3)更新节点的状态;4)构建损失函数优化模型参数。该方法在最小节点覆盖、最大割以及旅行商问题中进行了实验。在最小节点覆盖实验中,相比CPLEX求解器得到的最优解,该方法的性能几乎接近最优解,同时该方法也具有很好的泛化性,在小规模图中进行训练,然后可以用来在大图中进行测试。在最大割问题中,相比于基准算法来说也是更优的。在TSP问题中, 对于大图的优化性能稍微逊色些。
通过可视化的方式对算法进行可解释分析,发现相比其他算法,如每步选择节点度最大的节点,该算法每次都倾向于选择那些能覆盖更多节点,同时避免破坏连通性的节点,从长远看,需要的节点更少,这也正是强化学习的优势,可以启发我们选择更加高效的贪婪算法。该算法提供了一个统一框架,适用多种图上的组合优化问题。
Fan C, Zeng L, Sun Y, et al. Finding key players in complex networks through deep reinforcement learning[J]. Nature machine intelligence, 2020, 2(6): 317-324.
虽然S2V-DQN方法已经具有很好的优化效果,但是在更大规模上的泛化能力还有待提高。因此,范长俊等人提出一种通用且可扩展的深度学习求解框架,适用于不同的瓦解场景,同时继续提升了模型的泛化能力,使得模型能在上千万节点规模的网络中都能有很好的性能。该工作尝试在网络瓦解问题上面实验,希望找到能使网络瓦解的最少节点集合。其中衡量模型的好坏可以使用ANC曲线下的面积来表示,纵轴表示复杂网路功能,横轴表示移除节点的比例。复杂网络功能又可以使用结构性功能指标(包括最大连通片规模等)和非结构性功能指标(如军事中的体系预警规模等)来衡量。
FINDER算法的框架同样采取了类似S2V-DQN这种结合图表示学习和强化学习的算法框架,但是存在一些不同,区别如下所示:
对于实验部分,作者使用两种连通性的计算方法(CN,ND)以及三种节点赋权方式(无权、度权以及随机权),共六种实验场景。在六种不同的网络瓦解场景中效果平均提升28.7%。此外,该方法具有很好的泛化能力,可以使用小规模模拟图上训练的模型来测试大规模真实的网络,这说明模型学到了网络瓦解的内在的策略。同时FINDER的计算效率也提升超过两个数量级,FINDER算法自己发现了更快瓦解复杂网络的策略。在加权网络中,FINDER优先选择cost-effective的节点,即代价不那么大,却能达到相同的瓦解效果。
Fan C, Shen M, Nussinov Z, et al. Searching for spin glass ground states through deep reinforcement learning[J]. Nature Communications, 2023, 14(1): 725.
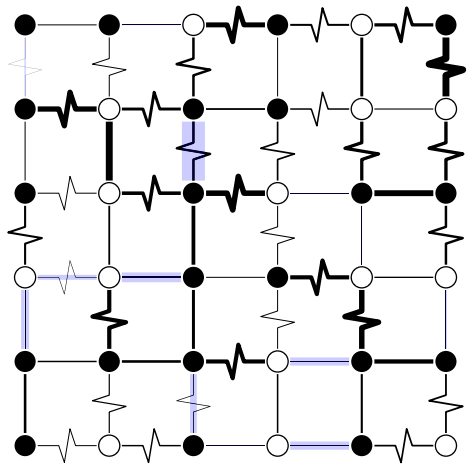
该工作尝试提出一种强化学习方法(DIRAC)来解决自旋玻璃的基态求解问题,确定最优的节点状态使得目标函数值最低,其中目标函数为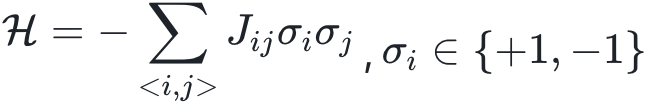 表示节点i的状态,每条边的权重
表示节点i的状态,每条边的权重 ,直线表示正权边,折线表示负权边,边的宽度与
,直线表示正权边,折线表示负权边,边的宽度与 呈正比,蓝色阴影部分表示边的能量
呈正比,蓝色阴影部分表示边的能量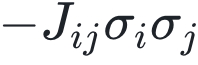 。
该方法同样基于图表示学习与强化学习框架,其中每个部分都有小的改动以适用自旋玻璃的基态求解问题。其中,基态求解问题受边权的影响很大,边权直接影响最终基态的分布,所以这里采用两阶段的嵌入方式,首先基于两端节点的嵌入向量更新边的嵌入向量,然后再基于相邻的边的表示更新节点的表示,这种方式能更好地捕捉边的特征与权重。
此外,最关键的是添加了规范变换的技巧(Gauge transformation)。引入变换在于,传统的强化学习工作流程存在缺点,只能从某个状态出发,逐步增加元素(动作选择)构建解集,直到满足终止条件,每个节点选择且只能选择一次,但是,这种方式最大的问题在于动作不可重复选择,即只能产生单个“最佳猜测”。然而,组合优化问题巨大的探索空间要求智能体能够重复多次“试错探索”以避免陷入局部最优,该工作提出的规范变换能够将任意状态转化为指定的状态,从而适合智能体的重复探索。规范变换带来如下好处:1)允许模型在一次探索(DIRAC1)结束后接着继续探索(DIRACm);2)允许模型从多个不同初态出发,从而取得更优的结果;3)允许模型和任意启发式算法结合,从而进一步提高启发式算法的结果;对性能的提升作用很大。
实验结果上,在大尺寸系统中(基态未知),DIRAC 相比目前最先进的退火算法,可以取得更低的能量。在小尺寸系统中(基态已知),DIRAC 均能求出全局最优解。此外,通过模型的可解释分析发现,该模型是通过牺牲短期收益,获取长远收益,这也是强化学习的优势所在。
该问题是揭开自旋玻璃奇怪而复杂行为的关键,有助于解决许多组合优化难题,有助于神经网络优化工具的开发。该算法具有以下优点:1)精度高,中等尺寸的系统可以达到全局最优解,且适用于三维及以上的高维系统;2)可扩展性强,最大系统尺寸达到三维的 L=20,这是目前研究最大的系统;3)可以和任意退火算法等启发式算法结合,并进一步提高这些算法的表现。
总之自回归方法中基于图表示学习加上强化学习是目前一种主流的研究范式,优点在于模型泛化性能好、模型效果好且具有一定的可解释性。但是存在模型设计、学习难以及实现困难等缺点。因此,作者也正在开发一种基于图表示学习和深度强化学习的图上组合优化问题求解工具(OptiGNN)来降低我们的学习门槛。
。
该方法同样基于图表示学习与强化学习框架,其中每个部分都有小的改动以适用自旋玻璃的基态求解问题。其中,基态求解问题受边权的影响很大,边权直接影响最终基态的分布,所以这里采用两阶段的嵌入方式,首先基于两端节点的嵌入向量更新边的嵌入向量,然后再基于相邻的边的表示更新节点的表示,这种方式能更好地捕捉边的特征与权重。
此外,最关键的是添加了规范变换的技巧(Gauge transformation)。引入变换在于,传统的强化学习工作流程存在缺点,只能从某个状态出发,逐步增加元素(动作选择)构建解集,直到满足终止条件,每个节点选择且只能选择一次,但是,这种方式最大的问题在于动作不可重复选择,即只能产生单个“最佳猜测”。然而,组合优化问题巨大的探索空间要求智能体能够重复多次“试错探索”以避免陷入局部最优,该工作提出的规范变换能够将任意状态转化为指定的状态,从而适合智能体的重复探索。规范变换带来如下好处:1)允许模型在一次探索(DIRAC1)结束后接着继续探索(DIRACm);2)允许模型从多个不同初态出发,从而取得更优的结果;3)允许模型和任意启发式算法结合,从而进一步提高启发式算法的结果;对性能的提升作用很大。
实验结果上,在大尺寸系统中(基态未知),DIRAC 相比目前最先进的退火算法,可以取得更低的能量。在小尺寸系统中(基态已知),DIRAC 均能求出全局最优解。此外,通过模型的可解释分析发现,该模型是通过牺牲短期收益,获取长远收益,这也是强化学习的优势所在。
该问题是揭开自旋玻璃奇怪而复杂行为的关键,有助于解决许多组合优化难题,有助于神经网络优化工具的开发。该算法具有以下优点:1)精度高,中等尺寸的系统可以达到全局最优解,且适用于三维及以上的高维系统;2)可扩展性强,最大系统尺寸达到三维的 L=20,这是目前研究最大的系统;3)可以和任意退火算法等启发式算法结合,并进一步提高这些算法的表现。
总之自回归方法中基于图表示学习加上强化学习是目前一种主流的研究范式,优点在于模型泛化性能好、模型效果好且具有一定的可解释性。但是存在模型设计、学习难以及实现困难等缺点。因此,作者也正在开发一种基于图表示学习和深度强化学习的图上组合优化问题求解工具(OptiGNN)来降低我们的学习门槛。
Solving Mixed Integer Programs Using Neural Networks
https://arxiv.org/abs/2012.13349
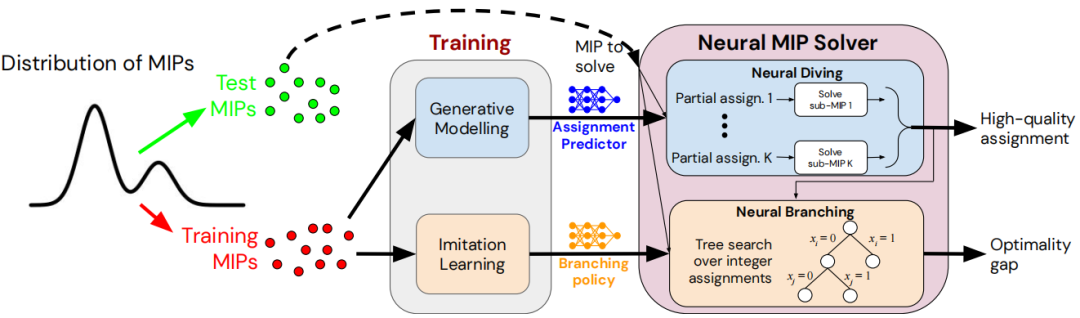
对于求解混合整数规划问题(MIP),最常见的精确算法就是分支定界算法,然而对于具体如何分支计算是很复杂的,传统的方法都是把它松弛到线性规划,然后用线性规划求边界,再选择相应的值。然而这样的方法计算量就非常大。现在可以使用机器学习方法把分支问题看成是一个二分类问题。如 DeepMind 提出用神经网络求解混合整数规划,包括 Neural Diving 以及 Neural Branching 两个部分,Neural Diving 训练一个深度神经网络来产生MIP问题部分整数变量的赋值,剩余未赋值的变量定义了一个更小的“子MIP”,这个子问题使用现成的MIP求解器(如SCIP)来求解,进而产生一个高质量的联合变量赋值;Neural Branching 训练一个深度神经网络,在经典求解器进行分支定界的过程中,针对给定节点模仿专家的分支变量选择策略进行分支变量的选择。
具体来说,可以将MIP建模为一个二部图,决策变量和约束看成图中的两类节点,其中变量前的系数和约束作为节点和边的特征。然后使用图神经网络生成部分解,具体来说可以将构建的二部图输入图卷积神经网络得到每个节点的表示向量,接着经过MLP输出各个变量为某个值的概率。此外,在分支定界过程中,为了提高决策质量,使用模仿学习,来学习strong branching的专家经验。模型在速度和精度均取得出色的表现。
Mills, Kyle and Ronagh, Pooya and Tamblyn, Isaac. Finding the ground state of spin Hamiltonians with reinforcement learning. Nature Machine Intelligence, 2020.
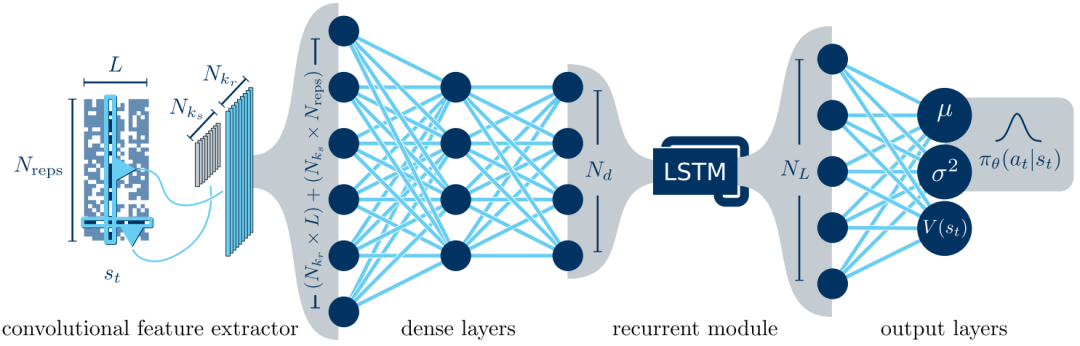
该工作尝试结合启发式算法解决自旋玻璃的基态求解问题,我们知道对于模拟退火方法,有个关键问题就是温度如何下降,为了克服这个问题,该方法利用强化学习学习模拟退火算法的最佳退火策略,然后使用最佳退火策略来求解自旋玻璃的基态。然而,该方法的实验结果并没有那么好。
图7 基于强化学习寻找自旋哈密顿量的基态算法流程图
Generalize a Small Pre-trained Model to Arbitrarily Large TSP Instances
https://ojs.aaai.org/index.php/AAAI/article/view/16916
对于如何提高大模型实例的泛化能力,下面讲解两个工作:
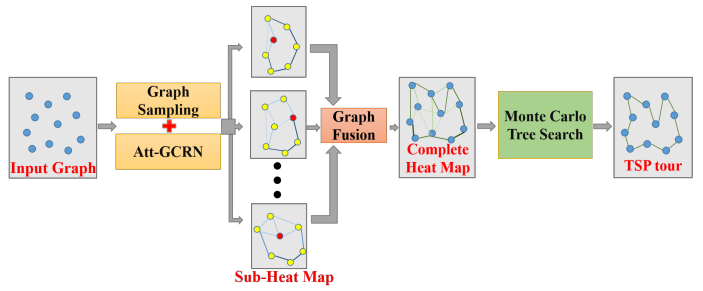
第一个工作使用监督学习解决经典的TSP问题,文章提出的是一种混合算法,级联了SL和RL模块。SL模块运用预训练的模型与三种图技巧(包括图采样、图转换、图合并)为任意规模的TSP构建热力图。热力图刻画了节点之间每条边属于该TSP最优环游的概率。随后,热力图将作为RL模块的重要输入。RL算法将进一步使用蒙特卡洛搜索寻找最优解,输出TSP的最优环游。该工作具有很好的泛化能力具体体现在如下操作,训练一个小规模网络的预训练模型,对于任意大规模的图输入都可以通过对图进行采样构建子图,然后分别通过学习好的预训练模型,最后将子图合并成原始的大图,解决了训练和测试图的尺寸不一致的情况。但是该方法应用也有限,该方法无法与强化学习方法进行结合。
第二个工作是前文提到的 FINDER 算法框架。在FINDER方法中,作者也尝试使用配置模型来提高模型的泛化能力,即定制匹配目标网络的训练数据,可以根据目标网络的度分布采样构建一个小规模图,然后在这些生成的图上训练模型。实验发现该方法能提升一些性能但是提升不是很大,同时针对特定的网络都要重新训练增加了模型计算量。
总之,这两个工作一定程度上提升了大模型的泛化能力,但是也带来了计算量的增加等问题,需要进一步的完善。
DC3: A learning method for optimization with hard constraints
https://arxiv.org/abs/2104.12225
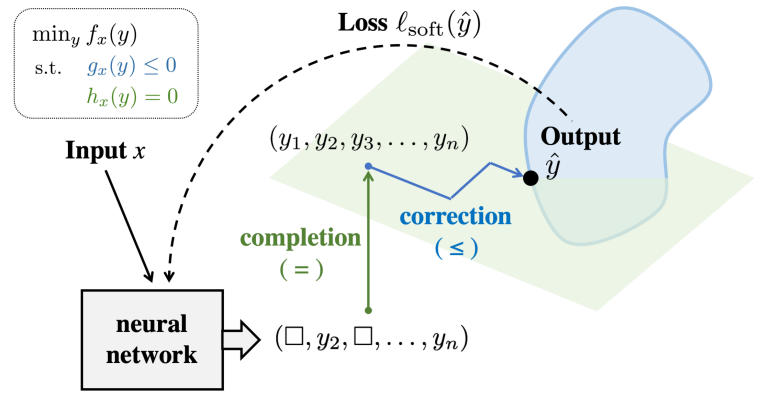
DC3这个工作尝试解决带有复杂约束的优化问题,这里的变量都是连续的,同时存在等式约束以及不等式约束。具体来说,如果决策变量有N个,同时存在M个等式约束,那么一开始我们使用神经网络先求得N-M个符合要求的解,然后使用等式约束求出其余的变量值,同时使用不等式约束来修正得到的解,最后计算损失函数反向更新参数来优化模型,其中损失函数具体包括三部分:目标函数、不等式约束以及等式约束损失。该方法的优点在于计算时间非常快,缺点在于目前的约束还是停留在线性约束上面,如何拓展到非线性约束也是一大挑战。
对于与成熟的求解器结合结合解决组合优化问题也是一大研究热点,下面具体介绍两个工作:
Differentiation of Blackbox Combinatorial Solvers
https://openreview.net/forum?id=BkevoJSYPB
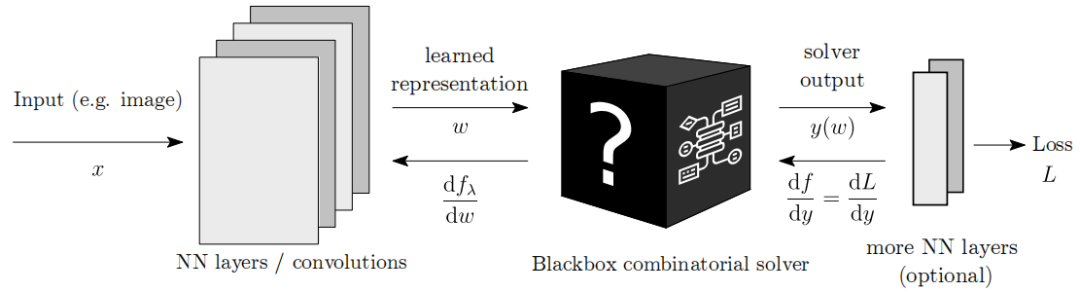
BlackBox 这个工作尝试将组合优化求解器变成深度学习模型中的可微构建块。具体来说,由于一个输入如图像等经过神经网络会得到连续的表征,然而求解器需要离散的输入。因此,该工作的重点是考虑如何将连续的表征转换成求解器的输入,反向梯度更新时又能将求解器的离散输出转换为神经网络的连续输入,训练一个端到端的框架。该工作的优点在于如果需要求出图片中两个点之间的距离,只需要输入一张图片,不需要对图像进行栅格化等额外操作,模型直接输出两个点之间的最短路径。
Network planning with deep reinforcement learning
https://dl.acm.org/doi/10.1145/3452296.3472902
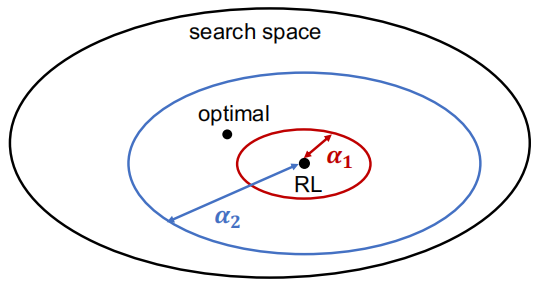
该工作提出一个两阶段的优化方法尝试结合深度强化学习与精确求解器(NeuroPlan)来解决一个资源调度问题。为了克服精确求解器无法求解大规模的优化问题的困难,作者将优化过程分为两个阶段:第一个阶段使用强化学习方法学习一个离最优解较近的结果,缩小搜索空间的范围;第二阶段使用精确求解器求得最优解。在小规模优化任务中,对比只使用强化学习的方法,该方法能有更好的优化效果,同时能媲美精确求解器方法。此外,在大规模优化任务中,该方法同样能取得了最好的优化效果,然而对于精确求解器来说,超出了其求解规模导致无法计算。
在与成熟的求解器结合的工作中,可以处理图像输入,那么随着ChatGPT的出现,其能够理解自然语言的问题需求,使得以后根据问题理解直接自动建模并调用求解器求解成为了可能。
斑图链接:https://pattern.swarma.org/article/240
范长俊:国防科技大学系统工程学院副教授。研究方向包括图深度学习、组合优化、强化学习及其在智能决策、复杂系统和指挥控制中的应用。以第一作者或通讯作者在Nature Machine Intelligence、Nature Communications、AAAI等顶级期刊和会议发表论文多篇。
现实世界中大量问题的解决依赖于算法的设计与求解。传统算法由人类专家设计,而随着人工智能技术不断发展,算法自动学习算法的案例日益增多,如以神经网络为代表的的人工智能算法,这是算法神经化求解的缘由。在算法神经化求解方向上,图神经网络是一个强有力的工具,能够充分利用图结构的特性,实现对高复杂度算法的高效近似求解。基于图神经网络的复杂系统优化与控制将会是大模型热潮之后新的未来方向。
为了探讨图神经网络在算法神经化求解的发展与现实应用,集智俱乐部联合国防科技大学系统工程学院副教授范长俊、中国人民大学高瓴人工智能学院助理教授黄文炳,共同发起「图神经网络与组合优化」读书会。读书会将聚焦于图神经网络与算法神经化求解的相关领域,包括神经算法推理、组合优化问题求解、几何图神经网络,以及算法神经化求解在 AI for Science 中的应用等方面,希望为参与者提供一个学术交流平台,激发参与者的学术兴趣,进一步推动相关领域的研究和应用发展。读书会从2023年6月14日开始,每周三晚 19:00-21:00 举行,持续时间预计8周。欢迎感兴趣的朋友报名参与!



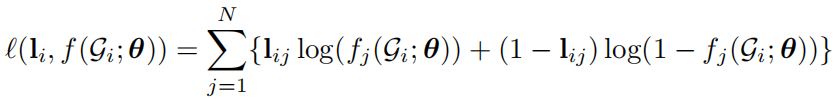
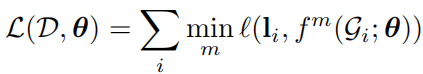
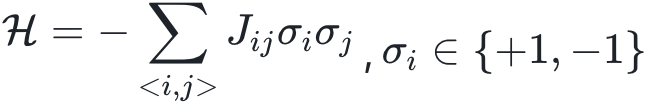 表示节点i的状态,每条边的权重
表示节点i的状态,每条边的权重 ,直线表示正权边,折线表示负权边,边的宽度与
,直线表示正权边,折线表示负权边,边的宽度与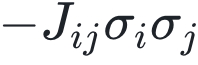 。
。