2020年以来，人类社会的发展仿佛呈现出一条全新的轨迹：极端天气、俄乌冲突、股市熔断、粮食危机，这些百年罕见的天灾人祸、重大事件集中发生。与此同时，以人工智能、区块链、元宇宙等颠覆性技术为代表的高科技产业仍在不遗余力地加速推进着。人们乐观地以为新的问题只有通过新的技术变革才能解决，但其实每一项新的发明都有可能引发新的问题和挑战。人们不禁要问：这意味着什么？这个疯狂的世界将要奔向何方？

要回答这一系列问题，应对人类百年未有之大变局，就必须站在一个全新的视角上进行系统性的思考。首先，这一全新视角需要抛开所谓“学科”的狭隘局限，将古今中外各个学科的知识统合起来；其次，它要求我们既要站在全球的宏观视角把握大的发展趋势，又要深入细节，给出精细微妙的处理方案；最后，它还要求我们必须认识到所有这些问题都并非彼此孤立，其背后存在关联性与统一性。总之，我们需要一个新兴的学科作为思维的脚手架，帮助我们理解这个复杂的世界。

复杂科学（complexity science）无疑将承担起历史的重任。这门自20世纪80年代发展起来的新兴学科试图采用跨学科的方法，研究各类复杂系统背后的统一规律。尽管它还很年轻，还没有一个普遍公认的概念体系和学科框架，但是它的跨学科范式、多尺度的研究视角、超越还原论的研究方法以及普遍联系的世界观，足以让它担此重任。

《规模法则》讲的正是复杂科学研究和关注的问题。首先我想讨论的一个问题是，这本书中的内容，按照我们一般的知识经验和学科框架，应该归于哪一个部分？我想这对于读者而言是十分重要的。显然，大家都会从书名和内容简介中意识到这本书将是极其有趣的，却又有些陌生：应该把它装进我大脑中的哪个学科板块呢？

我们对“量变引起质变”都非常熟悉，它揭示了当事物量的变化超过一定界限就会引发质的变化的规律，事物的本质差异由质所决定，不同的质往往对应不同的量的范围。可以看到，规模、大小、多少等都是量的基本内涵。这就要求我们在实践中把握适度原则，“施必适其量”。

然而，对不同的事物或者系统而言，与它们本身相适应的量，比如大小、规模、寿命等，应该是多少呢？这些量是否遵循相同的规律？这个规律具体又是什么？或者说，量变引起质变，进而导致事物由此变彼，可这背后还有不变的东西吗？这些问题正是本书试图回答的。万有引力不变，质量、能量守恒，这些都是物理学的普适原理。除此之外，对于复杂系统研究也许还有“新万物理论”——规模法则。

由此，回到开头的问题，规模法则似乎该归类为物理学。然而它的研究对象横跨整个自然界与社会，从细胞到企业甚至国家，显然并不局限于物理学范畴。实际上，学科的门类曾是为了方便人的认知而划分的，今天，我们是时候打破它们之间的壁垒了。我们不妨开拓一块新的领地来存放它，这里将弱化甚至摒弃学科间的差异，为我们认识事物提供一个新视角，一个新工具。

规模法则是什么？简单来说，规模法则力图对具有不同规模的事物一视同仁，无论它是生命系统还是非生命系统，无论它来自人类社会还是自然界，都力求找出它们背后共同遵循的规律。规模法则研究各种看似毫不相干的对象的各种宏观表征随系统规模变化的规律，且这些规律通常能够用一个简洁的幂律公式概括。

如何理解幂律？比如马太效应，也叫二八定律，每个人都耳熟能详，它广泛存在于社会财富、市场份额、网络流量、学术引用等的分布及资源、声誉和权力等的分配中，即绝大部分的收益被少数人占有，大部分人只能分享剩余的很少收益。在统计上，它们都服从幂律分布。再比如，鲨鱼、钞票、人和股票价格的移动/变化共同遵循“莱维飞行”模式，即它们大多数时间移动/变化的幅度比较小，而少数时间则非常大。这些移动/变化的幅度也遵从幂律分布。科学家在很多真实系统中发现了幂律分布，与这些讨论系统中某一个量的分布不同的是，规模法则的幂律公式描述的是复杂系统的各类宏观变量如何随着系统规模的大小而变化。

从一般的时间角度来看，老鼠、人、大象之间的寿命差异很大，这是由它们巨大的体重差异所导致的不同新陈代谢率造成的，且它们的寿命与各自的体重都遵循同一个幂律公式。不同于一般时间的概念，如果将相邻两次心跳之间的时间间隔看作一个单位时间（也叫生理时间），这些物种的“寿命”却很相近，因为它们一生的心跳总次数几乎相同。也因为不同物种生理时间之间的差异，老鼠总显得毛毛躁躁，而大象则慢慢悠悠。那为什么它们一生的心跳总次数几乎相同？在生命体的生长过程中，为什么虾、鸡和牛都遵循相同的生长曲线？心跳总次数和生长曲线又是怎样被它们与规模之间的幂律关系所决定的？这些问题的答案都在本书中，有待大家自行探索。

似乎这些问题与我们的生活关系不大？但下面的事情却与我们息息相关。

在药品说明书上经常可以看到“儿童减半”的说明，严格来说这并不准确。规模法则告诉我们，当一个儿童的体重是成人的一半时，他应该服用的准确剂量是成人的60%。或许减半服用并不是多么严重的事，最多效果欠佳或见效慢。然而反过来，当成人按照儿童剂量的双倍服用时，则可能因药物过量导致严重的后果。而造成这种差异的原因，也是源于规模法则中幂律形式的非线性关系。

相比如何科学服药，我们可能更关注一些有关人类社会的大问题。比如，为什么科技进步放缓之后，内卷现象就会加剧？为什么城市生活节奏越来越快？对市场而言，如何从公司财报的销售总额估计它的运转效率、总资产和投资收益率？如何刻画互联网社区的用户黏性——无论这个社区是流量巨头还是新上线的小网站？对城市设计和管理者而言，随着人口增长，基础设施建设该如何规划？城市的犯罪率是否过高？是否应该制定以及如何制定合理的创新激励政策？超大城市的未来图景是什么？是否应该限制城市规模甚至适当逆城市化？在规模多大的城市中人们将不能忍受它所要求的快节奏生活？规模法则揭示了以上所有与规模相关的问题产生的内在必然性，也对它们一一作答。

在规模法则的数学描述中

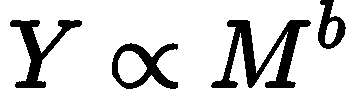
右侧的M可以看作对构成系统的物质规模的定量刻画，而左侧的Y可以理解为对系统的各种“能量”属性的度量，因此可以说规模法则描述了系统能量流与物质总量之间的定量关系。这个公式让我们自然想到爱因斯坦的质能方程及其所阐明的能量与质量之间的关系，不妨将其简记为

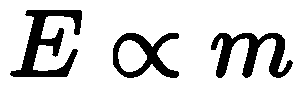
这两者无论是形式还是内涵，都是如此相似。更重要的是，从质能方程到规模法则，复杂系统从中悄然诞生。

除了规模法则的内容，它的探索过程本身也给予我们诸多启示。从鲁布纳的2/3次幂到克莱伯的3/4次幂，再到韦斯特等人的WBE模型，“第谷→开普勒→牛顿”的研究范式在这一过程中清晰呈现：首先将现象“采样”成数据，然后归纳建模现象层面的规律，最后探究现象规律背后的决定机制。这一研究范式并不限于科学实践，它是一种可靠的方法论，一种更高效的认知思维，无论你在什么行业和职位，都可以用它来更好地指导社会实践的方方面面。然而，在我们的实践中往往面临两个问题：一、只有数据而不清楚其背景；二、我们面对的大多数问题经常是细碎的，或者深度分工化的。因此，我们往往只见其部分而不见背后问题的全貌。这些问题经常导致我们难以准确把握现象层面的规律，更难以在决定机制的探索中有所建树。因此，我们应该花费一些精力从整个系统的角度去认识更全局性的情况，去适当地“逆分工化”，从而获得更深刻的认知和更长远的收益。正如二十大报告中所提到的“六个坚持”中的第五个坚持，就强调了将系统观念作为基础性的思想和工作方法。

而这种强调系统、整体的观念不仅可以追溯到老子这样的先贤的哲学思想，也秉承了近代科学巨人钱学森先生以整体与部分的关系为研究对象的系统论理论的研究脉络。复杂科学可以看作系统科学发展到当今世界的一个新阶段。不同于牛顿给人们描绘的一个机械性、确定性的世界：只要设定了初始状态，世界万物都将按照确定的规律运行，如同精心设计的机械钟表一样准确无误，复杂科学面对的往往是具有不确定性的世界，就如同大家熟知的蝴蝶效应，它形象地展现了非线性系统对初始值的极端敏感性，也体现了复杂系统一个有意思的现象——混沌。事实上，大多数真实系统既不是混沌的，也不是秩序的，而是处于两者之间，我们称之为混沌与秩序的边缘状态。复杂科学正是诞生于混沌与秩序边缘的新科学，它培养的是一种复杂性思维，而这种思维范式助力着我们对复杂系统中规模法则所展现出的普适规律的探索。

另外，我们需要看到，规模法则的形成，既是作者、韦斯特及更多研究者合作的结晶，更是跨越多个学科交叉研究的成果。今天，学科间的壁垒经常让研究和知识变得彼此陌生和难以沟通，这本身阻碍了人们对复杂的、宏大的、跨学科的问题的认识与研究，也阻碍了普适的“万物理论”的发现。甚至可能某些领域已经获知了一个新的“万物理论”，却因囿于狭窄的学科经验和不够开阔的视野而难以将其“举一反三”拓展到其他领域。正如克莱伯定律也需要跳出生物学范畴，在其他自然系统、社会系统、技术系统中验证之后，才能意识到它的“万物理论”的性质。

回到前文的“施必适其量”，它的后半句是“用必思其器”。让我们将本书的精华作为新的实践之“器”，超越现有的认知与经验，更深入地推进研究、认识万物、指导实践。