导语


了解神经系统中的通信和信息处理是神经科学（neuroscience）的核心目标。过去二十年来，连接组学和网络神经科学的发展为研究复杂大脑网络中多突触通信开辟了新途径，最近研究对连接组信号传递完全通过最短路径进行的主流假设提出质疑，从而产生大量可供选择的网络通信模型。

最新发表于Nature Reviews Neuroscience 的综述文章概述了大脑网络通信模型（brain network communication）的最新发展。作者首先从概念上将图论数学与神经信号的生物学方面（如传输延迟和代谢成本）联系起来，将主要的网络通信模型和测量方法归纳为一种分类法，旨在帮助研究人员浏览文献中日益增多的概念和方法，该分类法强调了连接组信号不同概念的利弊和解释。其次，作者通过回顾基础、认知和临床神经科学领域的突出应用，展示网络通信模型作为研究大脑功能的一种灵活、可解释和可操作框架的实用性。最后，作者提出指导网络通信模型未来发展、应用和验证的建议。

研究领域：复杂脑网络，脑网络通信，连接组学，网络神经科学
Caio Seguin, Olaf Sporns & Andrew Zalesky | 作者

董佳欣 | 翻译

刘培源 | 审校

论文标题：Brain network communication: concepts, models and applications
论文来源：Nature Reviews Neuroscience
原文链接：https://www.nature.com/articles/s41583-023-00718-5


目录

1. 引言

2. 从图论到脑网络通信

3. 脑网络通信模型和测量的分类法

4. 当前新兴应用

5. 未来展望和建议






1. 引言




神经系统是一种通信网络[1,2]，神经元之间的信号以及信息传递，渗透着大脑功能的方方面面及其空间尺度——从神经元到神经元的突触传递[3]，到神经元群之间的相互作用[4]，再到区域共振的全脑模式[5]。了解神经信号的灵活调控机制是现代神经科学经久不衰的挑战之一。为解决这一问题，需要横跨多个研究方向的努力，其中包括神经编码研究[6]、神经振荡的同步性和一致性研究[7,8]、神经元间通信子空间研究[9,10]以及神经动力学计算模型研究[11,12]。因此，关于通信网络的话题广泛延展，在神经科学中占据核心位置。

在过去二十年中，连接组学和网络神经科学已成为研究神经系统结构和功能时的重要领域[13-15]。网络神经科学为研究脑网络的复杂连通性如何促进、制约神经信息传递提供了一个框架[1]。这种研究方法得到大脑连通性综合图谱和图论数学的支持，与其他神经通信研究形成鲜明对比，后者通常侧重于少量物理连接的神经元或区域之间的信号传递[10,16]。相反，网络神经科学旨在通过解剖学上连接构造的复杂网络来了解多突触信号传递，以及神经通信是如何最终产生那些在神经系统中观察到的丰富功能动力学[17,18]。

结构性大脑网络——连接组[19]，是根据一系列复杂拓扑特性组织起来的，包括密集互联的枢纽核心[20]、模块化和分层结构[21]以及小世界架构[22]。这些大脑组织原则普遍存在于不同物种和不同空间尺度间[23]，据推测是由于高效神经通信的进化压力所致[24,25]。神经元间信号传递被认为能使远处的区域协调其活动，以应对不断变化的认知与行为上的需求[26,27]，而神经交流障碍可能与多种神经精神疾病的病因和症状有关[28-30]。因此，阐明支配连接组交流的机制，对基础、认知和临床脑科学的发展至关重要。


网络神经科学是最早、最有影响力的发现之一，其证明连接组是小世界网络[22,31]。与许多其他复杂网络类似[32]，大脑具有高度集群性——神经元倾向于形成紧密联系的群体；而且具有较短的特征路径长度——遥远的神经元对之间，平均只有少量的中间连接。这一发现为将大脑理解为兼顾功能分离和整合的网络提供了图论基础[24,33,34]。

除了描述连接组的组织特征外，早期网络神经科学中流行的小世界现象也使连接组通信假设具体化[15,35]。特征路径长度只考虑网络节点间步数最小的路径，从而量化网络整合，这同样适用于其他广泛用来研究大脑连接性的图测量方法，如全局效率和介数中心性[36]。通常在连接组通信和信号传输背景下进行解释时[25,33,37,38]，分析会基于这些测量假设——神经信号完全通过最短路径传递。

近年来，越来越多研究对最短路径假设提出质疑[39-41]。正如下文所述，这一方向的核心论点是，计算最短路径的前提是对网络拓扑全面了解[42,43]。这意味着要确定连接一对节点的最短路径，就必须了解网络中所有其他节点之间的连通性。虽然这一要求对于工程系统来说可能是合理的，因为在工程系统中，中央控制器通常可以鸟瞰整个网络，但脑网络是一种分散的系统，单个元素不可能拥有关于其所嵌入网络的完整信息[1,15,35,44]。

鉴于此，人们提出大量可供选择的脑网络通信模型[1]。从社会科学[45]到互联网工程[46]，这些模型受其他以分散网络通信为基础的科学领域启发，试图了解信息如何通过神经连通性以高效而又符合生物学原理的方式进行传输。大量新出现的证据表明，这些模型所产生连接组的通信测量结果与一系列生理[47,48]、行为[49,50]和临床变量[51-53]相关。

本综述总结了脑网络通信模型的最新发展，重点是利用图论和网络科学的概念来描述和量化结构连接组中信息传递的模型，主要目标是帮助研究人员浏览、应用和解释文献中出现的越来越多的方法。其余内容分为四个部分：首先，介绍本文使用的基本概念和术语，并将图论的数学概念与神经信号的生物学方面相联系；其次，将著名的网络通信模型和测量方法根据信号概念分类法进行归纳，从而提供文献概览，同时对网络通信模型的生物学合理性进行定性评估；第三，调查这些模型在基础、认知和临床脑科学等关键领域在当前的新兴应用，展示了网络通信作为研究大脑功能的多功能框架，并讨论支持不同信号概念的现有经验证据；最后，对未来进行展望，提出指导网络通信模型的开发、应用和验证的建议。




2. 从图论到脑网络通信




众所周知，神经元到脑区，结构连接有助于物理连接的神经元之间进行直接交流[3,54]。然而，对物理上未连接的神经元之间信号传递的观察了解较少。例如，秀丽隐杆线虫和黑腹果蝇幼虫的完整连接组以感觉神经元和运动神经元间的多突触信息流特征[55,56]；在人脑成像的宏观尺度上，有大量关于结构上互不关联的灰质区域之间的强功能共振模式（strong functional co-activation）的报道[57,58]；在局灶性脑刺激（focal brain stimulation）过程中获得的电生理记录显示，在未受刺激部位白质投射交叉（white matter projections）的下游区域存在一致的诱发反应[59,60]。这些例子说明神经动力学不仅由直接连接的元素间相互作用支持，还由遥远的、解剖学上未连接的神经元或区域的多突触通信支持，还展示了脑网络中信息传递的多种操作和研究方式——从微观的突触传递，到以多种时空分辨率下表现出的内在功能同步，再到局部外源扰动（local exogenous perturbations）的全局传播。

图论和网络科学为理解复杂脑网络中多突触通信提供了数学基础[13-15]。通过将生物神经信号抽象为网络通信动力学，这一理论框架提供了一种灵活方法来模拟相互连接的神经元间相互作用。

以图1a中宏观人类连接组为例，节点i和j代表一对没有通过轴突纤维束直接连接的脑区。考虑i和j之间如何建立通信？由于它们在解剖学上不相连，信号必须通过一系列中间区域和连接来传递，而连接组的复杂拓扑结构为i和j之间提供数量惊人的可能路径。脑网络通信模型描述了通过连接组传递信号的策略。

此文概述了脑网络通信模型的三个主要系列[44]。路由协议（Routing protocols）认为，信号是通过高效、选择性访问的少量路径传递的；扩散过程认为信号会在连接组中扩散，有可能同时沿着多个网络前端或按随机游走动力学传播；参数模型结合了路由和扩散的要素，根据模型参数的调整，提出倾向于通过有效路径或随机游走进行通信的混合策略。这三类中每一类都包含一系列具体模型。

图1 脑网络通信模型的核心概念。人类连接组是由灰质区域（网络节点）与白质束（网络连边）相互连接而成的宏观连接网络。通过复杂的大脑连通性进行多突触信号传播的指导原则是什么？通路和路径是图论中的概念，描述穿越网络的方式。通路被定义为一个连接序列，其中连续的一对连边共享同一节点。通路对节点和连边的遍历次数没有限制，是最无约束的网络遍历方式。在路径中，单个节点、连边只能经过一次，不允许信号重访网络元素。a. 区域i和j间有许多可能的通信通道，这些通道长度各不相同，表示它们支持快速且可靠信号传递的能力，最短路径是两区域间最高效的通道。b. 网络通信模型。结构连接矩阵表示n个神经元之间的物理连接，它只编码直接连接的节点间的信息，因此通常是稀疏矩阵。通信模型描述通过结构连接引导信号传播的策略，该模型确定了从节点i到j的路径（蓝色箭头）。通信测量方法量化该模型确定的路径的特征（例如效率、成本和弹性），从而得出从i到j的信号过程被推测会存在的特征。网络通信模型和度量可以在无向（双边连接）或有向（非对称连接）以及无权重（仅表示存在或不存在连接）或有权重（表示连接强度）的结构网络中计算。对于某些模型，连接权重需要转化为连接长度，以反映穿越连接的成本[15]。本综述中描述的大多数模型和测量方法的实现均可在“脑连接工具箱”（Brain Connectivity Toolbox）中找到[36]。b部分经授权改编自参考文献126，Elsevier。


网络通信模型将对神经信号的理解，如通过路由或扩散，形式化为一种明确定义的算法来引导信号穿过连接组。例如，该模型可以描述一种用于识别节点对之间的有效路径的程序。反之，网络通信度量可以量化给定模型下的信号传输特性，例如沿着模型划定路径发送信号的成本。通信度量可以反映信号传输的成本、效率、弹性或其他方面。在连接组上计算网络通信度量可得到一个通信矩阵，该矩阵可量化网络通信模型下每对节点（解剖学上连接或未连接）之间信号传递的推定属性（图1b）。

图1a中路径和通路作为区域间通信通道的适用性不相同。直观地说，由少量连接组成的“短”路径比穿过许多中间区域的“长”路径更有利，此处“短”和“长”表示沿该路径传播信号的成本，即路径长度。在i和j之间所有可能的路径中，最短路径最有效率。通过最大限度减少在两个节点间传递的步数，最短路径可以最大限度减少信号传输延迟以及穿过突触和沿轴突传播信号时的代谢消耗[15,61]。然而，路由信号要通过最短路径需要了解整个网络的拓扑结构[62]；因此，要确定i和j间最短路径的连接集合，就必须对单个网络元素可用拓扑信息量做出强有力的假设。

上一段介绍了网络通信成本的三个维度：延迟、信息和能量。延迟成本指信号传输的拓扑效率（或速度）；信息成本指引导信号传播所需的网络知识量；能量成本指信号传递所必须的代谢资源量。推测这些成本维度是进化驱动因素，它们塑造连接组的组织和信号机制以促进大脑快速、节约地整合信息[61,63,64]、还为评估候选脑网络通信模型的生物学合理性提供概念性指导[62]。理想模型将实现快速通信和经济的信号传输，并依赖于适合分散系统的知识假设，即低延迟、低能量和低信息成本。然而在实践中，以最短路径路由为例，这些因素很难调和，通信模型通常会在这三个维度之间做出权衡。正如下文中所述，某些信号的概念可以实现各因素间的良好平衡，有可能构成生物学上更合理的神经通信策略。




3. 脑网络通信模型和测量的分类法




本节将网络通信的系列、模型和测量方法编入树状分类法（图2），重点是描述不同模型的主要概念特征，并根据通信成本维度对其优缺点进行定性评估。方框1-3介绍了路由协议、传播过程和参数模型系列的主要网络通信测量指标。

图2 对脑网络通信模型和测量方法的分类。当前的脑网络通信模型可分为三大类——扩散过程、参数模型和路由协议，从分散（上）到集中（下）的策略。每个系列又分为多种通信模型，每种模型都提出特定的策略或算法来引导网络节点间的信号。可以根据通信成本的三个维度：延迟、信息和能量，从概念上评估一种模式的优缺点。这些维度的性能高低用颜色标签表示，分别为低、中或高成本。给定模型的性能可通过一系列通信指标来量化，衡量标准根据其量化的神经通信特征（如信号成本或弹性）进行分组并用颜色编码。AT，激活时间；Cinfo，信息成本；CMY，可交流性；Ctrans，传输成本（相当于 MFPT）；DE，扩散效率；EDP，边缘不连接路径；ER，效率比；k-SPL，k-最短路径长度；MFPT，平均首次通过时间；NE，导航效率；NPL，导航路径长度；PT，路径传递性；RE，资源效率；SI，搜索信息；SPE，最短路径效率；SPL，最短路径长度；SR，成功率。图经授权改编自参考文献116。


（一）路由协议


路由协议是一种网络通信模型，它认为信号在连接组中是沿单一、有选择的路径传输的。与工程网络中的传输过程类似，路由协议旨在找到由强大而可靠的少量连边组成的路径，从而高效、准确地传输信号。在连接组背景下，这种对速度和保真度的关注意味着路由模型具有低延迟、低能耗的特点[24]。但高效路径的识别通常依赖于对单个网络元素可利用知识的有力假设[44]，因此路由协议通常具有中等至较高的信息成本。

最短路径路由（shortest path routing）。最短路径路由是描述脑网络信息整合最广泛使用的通信模型[14,36]。该模型认为两区域间的信号传递沿着连接它们最有效路径进行。因此，根据定义，最短路径路由可实现最佳信号延迟。这种模式的选择性特征为，通信只通过最短路径进行，也意味着信号传递在新陈代谢消耗方面是最节俭模式。然而，该模型的主要缺点在于，用来确定最佳通信路由的算法程序要求每个网络元素都掌握整个网络的知识[42,43,45]。因此，最短路径路由需要极高的信息成本，表明这种策略很难在分散的神经系统中实施[1,15,35,44]。尽管可以设想用神经活动动力学地编码网络拓扑信息，但目前这种全局连通性的证明仍处于缺乏状态。最短路径路由模型下的信号传递可通过几种网络通信测量方法进行量化（方框1）。

导航（navigation）。导航是一种去中心化的路由协议，并不要求单个节点掌握网络拓扑的全局知识[42,45]，它提出了一种基于节点距离度量的局域知识来确定通信路径的策略[65]。从源节点到目标节点的路由遵循一个简单策略：从源节点开始，每个节点将信号转发给距离目标最近的邻节点。导航通常也被称为“贪婪路由”，因为通信过程中的每一步都是为了最小化与目标的距离，但这种探索式的方法并不能保证找到节点间的有效路径。事实上，与大多数网络通信模型不同，导航下的信号传递可能会失败，贪婪路由可能会陷入中间节点间的循环，永远无法到达预定目标，然而，复杂网络具有很高的导航性[43,66]。这意味着导航可以成功地在节点间传播信号，并通过识别路径达到与最短路径相当的效率（方框1）。

成功的网络导航必须以能反映节点对形成连边概率的距离指标为引导[43,67]。宏观脑网络导航的一个简单方法是考虑节点间的欧氏距离,这一选择动机是大脑在三维空间中的自然嵌入及其结构连接强度与欧氏距离间的密切关系[68,69]。值得注意的是，在人类、小鼠和猕猴的连接组中，欧氏空间贪婪路由能找到具有70-100% 的最佳信号效率（与最短路径相比）的路径[41]。最近的研究表明，人类的连接组导航也可以由大脑皮层分级引导，其中导航路径是根据从单模态到跨模功能轴的区域间距离确定的[70]。网络几何学领域的另一种研究方向[71]提出将大脑网络嵌入双曲空间，这是一种结合了空间和拓扑网络特征的抽象几何学[72,73]。

导航的主要缺点是信息成本高，信号传播的前提是各区域知道其邻近区域与所需目标区域之间的距离。虽然有证据表明在某些生物系统中可以满足这一要求[74]，但目前尚不清楚组成大脑网络的各个神经元如何获得这一知识。重要的是，导航的信息成本仍大大低于最短路径路由，导航以分散迭代的方式展开，路径上的每个节点只需要关于其邻居与相对的目标空间定位的局部知识，而不需要整个网络全局知识。尽管导航具有分散性，但其延迟时间与最短路径相当[41]。此外，由于信号被模拟为完全沿着导航路径展开，所以这一策略的能量成本也很低。因此，导航在中等信息成本与低延迟、低能量成本之间取得平衡，有可能成为比最短路径更符合生物学实际的路由策略。

方框 1
路由测量：通信效率基准

最短路径长度量化了两个节点间尽可能小的传输成本或延迟（见图）。它可以用路径上的步数或连接长度总和来定义。值得注意的是，由于通常假设神经通信是沿着最短路径进行的，因此这一指标通常被简称为“路径长度”。网络的特征路径长度是小世界架构的基石之一，它被定义为所有节点对最短路径长度的平均值[32]。另一种方法是用效率来量化通信，最短路径效率被定义为最短路径上连接长度的倒数之和，而一个网络的全局效率则由其所有节点对的平均最短路径效率决定[162]。对于任何网络，最短路径路由都提供了通信效率的上限。因此，最短路径测量通常被用作评估其他模型相对效率的基准。

可导航性是一个广义术语，指导航作为一种网络通信模式的性能。成功率是衡量导航能力的最基本指标，它被定义为可通过导航成功到达的节点对的比例[43]。在路由成功的情况下，导航路径长度和导航效率的定义类似于最短路径，即导航路径的连接长度。而导航失败的特点是路径长度无限。导航与最短路径路由的基准是效率比[41,163]，计算方法是最短路径长度与导航路径长度之比（见图）。

路由往往遵循“细粒度、粗粒度、细粒度”的传播模式。最初，通信发生在源节点附近，一旦到达一个本地的高度节点后，长距离连接就会促进以较小步数穿越较大距离，最后当到达目标节点附近，信号就会返回其最终目的地。这种模式（见图）在最短路径和导航路径中都能观察到，同时依赖于高聚类（支持对局域连通性的细粒度探索）和互联枢纽核心（允许长距离快速通信）[25,43]。

（二）扩散过程


扩散过程提出一种分散的神经通信概念，过程中信号沿着多个网络前端进行广播，或通过随机游走动力学传播。与路由协议不同的是，扩散过程不要求单个神经元掌握其周边以外的连接组知识，然而这种传播方式需要更多信号重传才能建立节点间的通信。因此，这一系列的模型通常受益于较低的信息成本，但却承受着较高信号延迟和能量成本。

随机游走（random walks）。随机游走是最流行的网络扩散过程模型，被广泛用于研究各种科学领域的复杂系统动力学（见参考文献 75 的全面综述）。这里重点讨论无偏随机游走，它是网络扩散的最简单形式，也是备受关注的脑网络通信模型。

在随机游走中，信号从源节点出发，以与连接权重成正比的概率传输到随机选择的邻近节点，每个新节点都遵循这一规则，直到最终到达目标节点。这一过程被称为“无偏”，因为下一个节点的决定完全基于局域连接，没有其他因素影响信号传播。要实施这一策略，节点只需了解自身的连通性，这一假设可以通过单个神经元来实现。随机游走的信息成本低，但延迟和能量成本却很高，直观地说，随机信号传播会导致行走路径明显长于最短路径，信号在许多突触连接点和轴突突起之间的再传递使得区域间的交流变得缓慢且代谢成本很高。

与这一概念评估相一致，实证研究发现，在人类连接组中，随机游走导致信号传递效率低下[44,63]。评估方法是使用平均首次通过时间[76]，该指标量化了随机游走从给定源节点出发后首次访问目标节点所需的平均步数。扩散效率[44] 被定义为平均首次通过时间的倒数。这些测量值可解释为从源节点到目标区域的预期行走长度和行走效率，这一概念类似路由协议的测量值。更有趣的是，除了信号传递效率本身，还有一系列基于扩散的实用测量方法可以量化大脑网络拓扑结构与随机游走动力学间的相互作用（方框2）。

广播（可传播性）（broadcasting (communicability)）。广播是一个扩散过程，信号同时沿着网络的多个前端传播。到目前为止，我们所探索的传播模型都是通过路由协议或随机选择来确定信号下一步应该发送到哪个节点。相反，在广播的每一步，信号都会同时传播到许多节点。我们重点讨论可传播性[77,78]，这是一种在大脑网络中被广泛探讨的特定广播模型。

可传播性认为信号会沿着网络中所有路径传播。为了理解这一点，可以考虑一种简单的广播策略：从信号源开始，各区域总是将信号传播给所有的邻居。最初，源会将信号发送到与其直接相连的区域，第一步是从源点出发，划定所有单位长度的路径，随后所有接收到信号的区域都会将信号传播给所有相邻区域，从而划分出从信号源开始所有长度为2的可能路径。重要的是，这个过程与某个区域是否已经接收到信号无关，所有长度为2的行走集合包括回溯到信号源的行走以及在信号源邻居之间重新传播信号的行走（如果它们之间存在连接）。第n个广播是步长为n的所有路径集合。最终，从源节点到目标节点的信号是由它们之间所有长度为n = 1, …, ∞的行走形成的。

两个节点之间的可通信性可以计算它们行走总次数的加权和（方框2）。每条路径的贡献都根据1/ ! n进行加权，从而确保短路径比长路径更重要。因此，通信主要是沿着短路径进行的，随着路径变长，低效路径的总体贡献会迅速消失。

两个节点之间所有可能的路径集合包括它们的最短路径。由于信号会同时沿所有路径扩散，因此在广播情况下，信号从首次离开信号源到首次到达目标之间的延迟与最短路径路由的延迟相同。然而，直观上看，这种策略需要极高的新陈代谢消耗，虽然这种缺陷会随着长距离行走的减少而减弱（因为长距离行走的贡献会随着时间推移而减少，所以可以假设它们的能量负担也同样会减少），但可传播性仍然需要大量的信号重传。总之，广播的形式实现低延迟和低信息成本，但却带来高能耗成本。

方框 2
差异度量：连通性如何自发形成传播


许多差异度量描述了随机游走与最短路径间的关系，反映了网络拓扑结构自发引导随机游走沿有效路径展开的程度。搜索信息[164,165]量化了使随机游走沿两个节点间最短路径展开所需的努力（以信息比特为单位）。这一指标与网络中有效路径可达性有关。局部连通性（见图中a部分；黑色虚线箭头）有助于偏离最短路径（蓝色箭头），从而提高搜索信息量。同样，路径反向性[39]被定义为沿最短路径的局部迂回密度。局部迂回是指短暂偏离最短路径，但在下游节点又回到最短路径的连接序列（见图中b部分；黑色虚线箭头），从而有助于将信息流集中在高效路径上。

资源效率[44]的定义是，在给定概率下，确保至少有一个信号沿最短路径在源区和目标区之间传播所需的随机游走次数。这种独特的测量方法旨在量化路由和扩散之间的成本-效率权衡，假设随机游走的低效率可以通过增加信号副本的数量来改善。通过投入更多资源（信号副本），随机游走模型可以在保持低信息成本的同时实现低延迟。显然，效率的提高是以更高的新陈代谢需求为代价的。

可交流性[77,78]提出在所有网络行走中同时广播信号，因此实现资源效率测量的最极端方案。可交流性的独特之处在于，它既是一种交流模型，又是一种衡量标准，因为它将广播的概念与量化其属性的特定表述相结合。具体来说，高（低）可通信性表明两个节点之间存在多（少）条有效路径，这一特性可解释为通信弹性和并行信号的整体能力[15]。可沟通性是网络神经科学中一种流行的测量方法，是最短路径测量方法最常用的替代方法之一。a部分经授权改编自参考文献116，Elsevier。

（三）参数模型


这一系列模型的显著特点是它们的行为由可调参数控制，可调参数沿一连续可能值定义。在这个范围两端，参数值通常近似于通过路由或扩散进行通信，而中间值则实现混合策略。对参数进行仔细调整后，就能产生复合策略，在延迟、信息和能量成本之间实现有利权衡，而这是路由和扩散，两种截然相反的策略，所无法实现的。

线性阈值模型（linear threshold model）。线性阈值模型旨在描述单个节点的扰动如何在网络中传播[79,80]。该模型与上文中广播密切相关，其认为局部扰动会触发通信级联，并沿多个网络前端传播。在任何给定时间点，认为节点处于“活跃”或“不活跃”状态，前者状态下的网络元素代表扰动已传播到它。向节点的传播以其邻近节点状态为基础——如果邻近节点中有足够大的比例处于活跃状态，则该节点就会处于活跃状态。这一比例由模型的阈值参数θ∈[0,1]编码，该值可控制级联的速度和规模（方框3）。

设置θ= 0 可以实现一个广播过程，过程中信号总是传播到活动节点的所有邻居。这种情况下，任何节点的扰动都会导致激活迅速扩散到整个网络，称为完全级联。随着θ的增大，节点邻域中需要更大比例的“活跃”节点来进行传播，级联变得更慢、更小。临界值θ=θc是单个节点受到任何干扰都会导致完整级联现象的最大阈值，超过临界值，信号传递就会越来越局限于信号源附近。

迄今为止，将线性阈值模型应用于脑网络时，考虑的是θ=θc（参考文献 81-83）。这些研究报告指出，完整级联的轨迹在很大程度上受有效通信路径的影响[81]。重要的是，级联的扩散是由节点激活的局部知识决定的——节点的激活完全基于近邻的状态。因此，连接组拓扑结构与线性阈值模型之间的交互作用会以较低信息成本产生良好的信号效率。与广播一样，这些优势也是以高能耗成本的多次信号传输为代价的，但重要的是，与可通信性相反，线性阈值模型不考虑向已处于“活跃”状态的节点进行多次重传。因此，就能量成本而言，线性阈值模型的能量成本适中，介于扩散模型和路由模型之间。

有偏随机游走（biased random walks）。在无偏随机游走中，信号仅使用局部拓扑知识进行预处理，即对于当前节点i，游走以与ij连接权重成比例的概率过渡到节点j。相比之下，有偏随机游走使用额外因素来影响（偏置）过渡概率[84,85]。在特定领域的应用中，偏差因素可以代表网络元素的内在属性（例如，某人在社交网络中的地位），从而影响向特定节点或沿网络梯度延伸的行走[86]。另外，随机游走也可能因拓扑属性而形成偏差，如节点中心性[87,88]。

我们将重点放在有偏随机游走的参数化表述上，该表述最近被应用于研究大脑网络中的通信[62]。在这一模型中，参数λ控制单个节点可利用的全局拓扑信息量。当λ= 0时，不引入任何偏差，节点只能获得自己的连接权重，因此通信通过无偏随机游走进行。增加λ会逐步引导游走沿着有效路线进行，具体做法是向节点提供信息，使其知道哪个邻居更有可能位于通往所需目标的最短路径上，并使过渡概率偏向于选择这个邻居。在极限λ→∞时，有偏随机游走收敛到最短路径路由，走到目标最短路径之外任何节点的概率变为零。

有偏随机游走跨越了从无偏随机游走到最短路径路由等通信策略的连续谱。因此，该模型在通信成本维度上的性能完全取决于λ值。更重要的是，该模型提供一种灵活的方法来探索大脑网络中的通信动力学，系统λ的变化允许对延迟和信息成本之间的权衡进行定量分析（方框3）。

最短路径集合（shortest path ensembles）。最短路径集合模型认为，信号在两个节点之间的传输通过连接它们的k条最有效路径组成的集合进行[40]。传统最短路径路由与 k = 1 的特殊情况相对应，这种情况下，信号只利用节点间一条最有效路径。最短路径集合突出表明，尽管高效率是自适应的，但并不存在神经通信只通过最优短路径进行的原理[15]。事实上，经验分析表明，只有一小部分连接是通过连接组中所有节点对间最短路径进行的[40,41]。因此，在严格最优路由机制下，大脑中绝大多数轴突都无法支持全局信号传输。将神经通信中涉及的路径数量参数化，可以系统放宽这一假设（方框3）。

与其他多路径信号模型不同的是，最短路径集合只考虑节点间最有效的前k条路径，因此对哪些路径支持通信仍有选择性。在k值较小的情况下，节点对之间k条最有效路径的确定仍然很大程度上依赖于全局拓扑知识。然而，当k>>1 时，路径集合变得庞大且具有包容性，其构建所需的信息成本也更低。同样，沿多条路径传输信号所需的能量成本也与k的选取成正比。考虑到所有可能的k，最短路径集合模型的特点是传输延迟低，同时平均信息成本和能量成本适中。

方框 3
参数测量：探索交流成本的权衡


激活时间是线性阈值模型的主要通信指标。它量化了网络受到扰动后两个节点激活间的延迟。结合阈值模型的可调参数，这种简单的测量方法可用于模拟复杂传播动态[166,167]，在神经级联计算[81,82]和证明[83]的研究中都很有用。

有偏随机游走会产生连续的传播策略谱，从而对延迟和信息成本之间的权衡进行定量分析。直观而言，经验性的连接组分析表明，增加λ（节点可用的全局信息量）会导致平均信息成本单调增加与节点对间平均传输延迟减少[62]（见图）。但重要的是，两种成本的变化率并不相同，λ值范围较窄时，信息成本和延迟成本变化率都较低，这表明，连接组拓扑结构可能是这样组织的：引入微妙的偏差因素可能会在通信效率方面带来不成比例的巨大收益。

为研究最短路径集合的特性，人们提出两种网络通信测量方法。k-最短路径长度是一种混合度量，它结合信号效率和信息成本的概念。k-边缘连接（k-edge disjoint）路径量化了集合中不与任何其他路径共享连边的路径数量。这是衡量通信对网络元素失效（如灰质区域退化）的恢复能力的一个指标[168]。对这些指标的分析表明，在连接组信号传递过程中存在一种权衡，即成对的区域倾向于以较高效率和较低弹性进行通信，反之亦然[40]。这表明容错性是连接组通信的另一个维度，与传输延迟、代谢需求和信息成本等概念相互交织[169]。Cinfo，信息成本；Ctrans，传输成本。图经授权改编自参考文献62。




4. 当前新兴应用




在本节将回顾脑网络通信模型如何用于研究一系列基础、认知和临床神经科学问题的突出实例（图3），通过这些例子展示模型如何为研究健康和疾病中的大脑功能提供一个多功能、可相互解释和可计算的框架。重要的是，实际应用也为模型验证提供了重要机会。上一节考虑了对生物学合理性的定性评估，而这节将根据模型对各种经验现象的解释能力来对模型进行比较。

图3 通信矩阵的当前新兴应用

网络通信模型和测量方法用于计算通信矩阵，矩阵将结构连通性的网络转化为神经元对间信号传递的定量估计（图1b）。a，功能连接矩阵捕捉神经活动时间序列中成对的关联。大量研究表明，通讯矩阵可以解释功能连通性的多个方面，包括全局[39,90]、系统级[126,154,155]和区域级[124,156]，以及大脑功能网络的静态和时间分辨[134,135]特性。这方面的大多数研究都考虑了静息态功能磁共振成像[18]的数据，但最近的研究正在将这些工作扩展到神经活动的电生理记录[48,116,157]。b，学科级（Subject-level）通讯矩阵可用于研究神经信号如何与认知、行为和临床变量相关联[28,95]。在全脑层面上，对通信矩阵的所有元素求平均值，可得连接组通信的单值摘要（single-value summary），可与所关注的表型相关联[38]。也许更有趣的是，通信矩阵的子集可用于检验特定区域或系统的假设，例如同位区之间的通信[53]或感兴趣的功能系统内部的通讯[50]。c，结构性损伤可通过动物模型中的受控操作进行研究，也可通过从连接组中删除节点和连边进行模拟[47,158]。对人类而言，交流测量已被用于模拟多发性硬化症[159]中风[53,160,161]和创伤性脑损伤[98-101]。d，患者的实际协调中断。通讯矩阵的行（列）量化传出（传入）的区域通信，第i行模拟刺激从第i区域向网络其他区域传递[116]，反之，第j列量化从所有区域到第j区域的传输。根据特定受试者的连接组进行计算，这些指标有助于完善临床脑刺激的个性化方案[118,120]并为选择刺激部位提供信息，以便通过非侵入性技术（如经颅磁刺激[117]）间接调节深层结构。

（一）连接大脑结构和功能


功能连通性描述神经活动在一段时间内的同步性。结构连通性以解剖学为基础，通常在短时间内是静态的，而功能连通性在多个空间和时间尺度上变化，从而产生了大脑丰富的动态剧目[17,89]。重要的是，神经活动的协调是通过解剖学上的连接发出信号来支撑的，所以交流过程是连接神经系统结构与功能的桥梁[1,18]。因此，脑网络通信模型最早的一些应用是研究结构连接和功能连接之间的关系（图3a）。

早期的报告确定了人脑中结构连接和功能连接之间的紧密相关性：根据扩散磁共振成像（diffusion MRI）和束流成像技术（tractography）推测出连接两个灰质区域的白质束越强，它们的活动时间轨迹往往越紧密耦合[19,54]。然而，这种关联仅限于解剖学上相连的区域，因此无法解释反向观察到的未通过白质直接连接的区域之间的强功能连通性[18,57,58]。

为了研究这个问题，2014年，Goñi等人[39]计算了人类连接组中多种网络通信测量指标，并用它们来预测从静息态功能磁共振成像（fMRI）推断出的功能连接性。作者发现，通过多突触网络通信量度量化的强大且可访问的通信渠道连接的区域对，显示出更高的功能连通性。有趣的是，与最短路径长度相比，基于扩散的搜索信息和路径传递性测量（方框2）更具预测性，这表明扩散动力学可能促进了区域间的交流。在当代一篇论文中，Abdelnour等人[90]使用另一种网络扩散模型得出类似的结果。这些研究共同提供了网络通信模型作为研究大脑功能的框架的最早的演示，以及连接组通信并非完全由最短路径决定的初步经验证据。

在这些奠基性论文发表后，通过静息态 fMRI 推断的功能连通性关联强度已成为验证和比较网络通信模型最常用的方法之一（有关这方面研究的其他例子，请参见图3a）。尽管这种方法硕果累累，但也存在重要缺陷。例如，静息态数据对与特定行为或认知需求相关的交流过程提供的洞察力可能有限，而使用基于任务的范式可以更好探索这些过程[91]。同样，在对大脑活动进行干预性操作的情况下获得的功能数据可以提供更强大的实验设备来验证和比较交流模型[92]。这方面的例子包括建立脑刺激传播模型，以及研究脑损伤或病理导致的功能连接变化。在接下来的章节中，我们将综述有关这些新兴脑网络通信模型应用的论文。

（二）认知和临床表型的个体间差异


人类的认知和行为依赖于多个脑区协同活动，现代神经科学一个核心研究方向是绘制功能连接特征与认知表型间的关联图[93,94]。网络通信模型可用于研究与不同认知需求相关的信号传导过程，以及连接组通信差异如何导致认知和行为的个体间差异（图3b）。同样，虽然区域间协调对大脑的健康运作至关重要，但连接组交流的异常已被认为与多种脑部疾病的病因和症状有关[28-30]。基于这些观察结果，有学者提出，连接组连接失调，大脑区域间信息不能正确整合，可能是精神和神经疾病共同病理的一个潜在层面[28,51]。网络通信模型提供了可操作化连接组失调和量化功能整合崩溃的工具，从而建立了一个平台，将大脑疾病状态特有的结构和生理改变联系起来。

迄今为止，这些方向的研究大多基于最短路径路由模型[36,38,95]。这种狭隘的关注点可能无法全面说明连接组的通讯和功能整合，从而无法发现感兴趣的大脑行为关系。事实上，最初的比较研究发现，替代模型往往比最短路径测量更能解释认知和临床变量。这方面的例子包括应用导航、可交流性和其他基于扩散的测量方法来研究健康人的信息处理速度[50]和一般智力[96]，以及精神分裂症患者[97]、阿尔茨海默病[52]、中风[53]和脑外伤患者[98-101]的认知和神经交流障碍。最近利用机器学习对不同测量指标进行系统比较的研究已开始揭示哪些模式具有更高的行为和临床预测效用[49]，这也是未来研究的一个重要方向。

（三）病变影响和病理扩散建模


在网络系统中，局部元素的破坏——如灰质和白质位置的损伤、萎缩或功能障碍，会先引发连锁效应，通过网络逐级扩散，从而影响整个系统的功能[102]。网络通信可用于研究和预测大脑功能如何受到结构性病变、断开和病理的影响（图3c）。

在2016年一篇论文中，Grayson 等人[47]利用药物遗传学干预方法来暂时停用恒河猴的杏仁核。作者发现，定向去激活后杏仁核间功能连接的变化并不局限于与杏仁核有直接结构连接的区域。这表明局部活动抑制会导致多突触信号中断，这种中断表现为全局功能连接的重构模式。为进一步探讨这个问题，作者使用可交流性模型来量化恒河猴结构连接组中的交流。通过将杏仁核从连接组中移除，利用电脑模拟药物遗传性失活，从而有效地阻碍了利用该区域作为信号传输媒介的可交流性。这就产生了一种结构性网络通信中断的测量方法，值得注意的是，这种方法与所观察到的功能连通性变化密切相关。这项工作提供了实验证据，证明网络通信模型可以预测灰质结构的经验性和非常规性破坏的功能性后果。在人类中，这一研究领域对理解病变后受损的大脑功能和认知结果具有重要意义。最近研究采用基于扩散的测量方法来研究脑外伤后的信号重路由和神经可塑性，从而深入了解通信如何绕过受损区域以恢复大脑功能并促进患者康复[100,101]。

在相关研究领域，网络通信模型也被用于描述病原体和神经变性在大脑中的逐渐扩散，许多神经系统疾病的逐渐蔓延被认为是由病原体（例如阿尔茨海默病中的错误折叠蛋白）跨突触传播导致的，因此是由结构连通性决定的[29,30,103]。在2012年一项颇具影响力的研究中，Raj等人[104]发现，痴呆症患者灰质萎缩的空间分布可以通过病原体在人类连接组中传播的扩散模型再现。随后的研究使用各种扩散和流行病学传播模型（概念上类似于线性阈值模型）来研究肌萎缩性脊髓侧索硬化症[105]、阿尔茨海默病[106]和帕金森病[107]中神经变性的进展。最近，精神分裂症[108,109]中也出现了皮质萎缩的跨突触推进证据，但网络通信模型在精神疾病进展中的应用仍有待探索。

这两项研究有望加深研究人员对脑损伤和病理与患者临床结果之间关系的理解。除了诊断生物标志物或组间差异外，前面提到的应用还促进了对预后洞察力的关注。在疾病或损伤开始时通过考虑个体自身的连接性和损伤位置，预测临床结果的能力，可能有助于解释病人的异质轨迹和长期结果[29,99]，未来需要将这些预测模型应用到临床环境中，并确定其在患者治疗中的效用。这方面的努力可能会受益于人口规模的纵向数据集，如英国生物库[110,111]，通过在未来几十年内追踪数以万计参与者的健康状况，数据包括患者在疾病或病变发生前的连接组，以及在临床诊断时的定期成像随访。这将有助于对各种脑损伤或病理表现的长期功能重组和信号路由进行纵向研究[100,101]，确定哪些网络通信模型在这些情况下具有更高的临床实用性将为模型验证提供重要途径。

（四）大脑刺激传播建模


从光遗传学技术[16]刺激单个神经元到直接电脉冲[59,112]刺激大型脑结构，刺激神经元的能力使得研究定向扰动的因果效应成为可能。微观和宏观研究的证据表明，局灶刺激的效应并不局限于最初的扰动点，而是通过内部连通性扩散[60,113-115]，因此，模拟脑刺激效应是一个典型的网络通信问题（图3d）。

在最近一篇论文[116]中，作者团队使用大量直接电刺激数据集来研究人脑中的经验信号传输。在对550名癫痫患者进行局灶性单脉冲刺激后，获得颅内脑电图记录。作者利用患者间和患者内电极位置的差异性，根据经验推断并按照神经信号固有的毫秒级时间尺度，绘制了全脑因果关系刺激传播图。作者在人类连接体上计算了一套网络通信测量方法，以量化区域间的传播，尤其关注解剖上未连接、空间上遥远的区域对，在这种情况下多突触通信最为相关。研究发现，通讯测量能够准确而稳定地预测通过白质连通性发出的信号，对不同预测因子的解释力进行比较后发现，搜索信息和可交流性优于其他交流测量指标，这一发现有助于深入了解白质连通性的复杂拓扑结构如何塑造局部脑刺激的全局效应（图4）。

这项研究表明，网络交流模式具有为临床脑刺激提供信息的潜力[117,118]。大量研究报告显示，刺激部位的连接情况与患者的结果有关[119-121]，表明治疗效果与刺激后大脑活动的分布变化相关。然而，目前对连接图的关注并未明确考虑通连接组的多突触传递。网络通信模型为解决这一难题提供了一个途径，在不同刺激方法和临床队列的背景下，确定网络通信模型是否有助于提高治疗性脑刺激的疗效是未来工作一个重要方向。

（五）简单模型的作用：借助可解释性和可操作性


脑网络通信模型可以简化解释神经信号，尽管这些模型在概念上与传输延迟和代谢消耗有联系，但它们并没有明确地以神经元生理学为基础。相反，按照复杂系统极简描述的传统[122,123]，这些简单模型有意抽象了神经元信号传导的微观方面，以捕捉神经动力学的突发性和全系统特性[62,81]。正如所看到的，这种抽象为描述和量化各种经验现象提供了一个共同数学基础。按照这一思路，本节将进一步探讨网络通信模型的两个关键优势：(i)能够产生可解释的洞察力，洞察连接组组织如何塑造网络通信模式；(ii)计算的可操作性。

对网络通信模型的解释取决于这样一种认识，即每种模型和测量方法都与底层结构连通性的不同特征相互作用，并依赖于这些特征。为举例说明这一点，考虑通过最短路径进行路由的模型和可传播性下的广播模型。路由完全依赖于由少量精选连接组成的高效路径，因此这些路径之外的网络元素与路由模型无关，进而也与任何基于路由测量的预测或统计解释无关。相比之下，可通信性则认为网络中的所有游走都有助于信号传递，因此可通信性衡量标准受更广泛的网络拓扑结构影响，例如，两个节点之间存在多条可供选择的路由会促进它们之间的通信。有了源自这两个模型的测量方法，研究人员就能确定路由还是广播更能解释感兴趣的实证观察结果。这就能揭示解剖连通性哪些特征与经验现象的神经生物学过程更相关（图4），比如这个例子中，最短路径的长度或多种通信路径的存在。

本文研究的通讯测量方法计算起来非常高效。在大多数情况下，它们构成结构连通性矩阵的分析转换，对于包含数千个节点的矩阵来说，只需几秒钟就能完成[36]。这一实际优势有助于对经验数据进行系统化和可操作性探索，例如预测数百个刺激点的电信号传播[116]和分析数千名受试者的个性化连接组[111]。此外，这一框架在计算上的可操作性也增强了其可解释性和产生洞察力的能力，因为它可以对来自不同模型相互竞争的假设和统计解释进行省时高效的测试[124-126]。

重要的是，尽管具有可解释性和可操作性的优点，但现有模型的简单性对研究调节灵活神经信号的生物机制构成了一定的障碍，也就是说，即使网络通信模型可以通过复杂的连通性量化信号传导路径，但它们对神经元活动如何通过一种路径与另一种路径进行传导的深入了解是有限的。人们已经提出多种机理假设，以神经元活动的同步性和一致性为基础来解释选择性信息传递[4,7,8,10,12]，但这些假设通常考虑的是物理连接的神经元小图案中的通信。在现有模型（不是侧重于大型复杂脑网络中的多突触信号）与更广泛的机理神经通讯研究之间架起桥梁，是未来工作的一个重要方向。

图4 网络通信模型的可解释性洞察力：脑刺激案例研究。a，通过局灶直接电刺激发出的脉冲在远处解剖学上未连接的部位引起皮质-皮质诱发反应。b，网络通信测量根据白质连接的不同特征量化通过连接组发出的信号。比较不同测量方法对刺激诱发反应强度（R）差异的解释程度，可以深入了解神经通讯动态。从节点A、B和C到目标节点T的最短路径长度（左图）完全基于它们之间最直接路径的连接。根据最短路径模型，刺激A、B和C所引起的反应应该是RAT > RBT > RCT。搜索信息（中心）与无偏随机游走从源节点沿最短路径到达目标节点的概率有关，该概率值由构成路径的节点的局部连接性决定。因此，搜索信息不仅对网络的最短路径结构敏感，而且对局部拓扑特征也很敏感。在脑刺激方面，搜索信息可以解释为刺激和目标点间的刺激分散倾向。尽管A、B和C到T的最短路径长度相同，但搜索信息预测RCT > RBT > RAT。可传播性（右图）考虑了通过所有网络路径进行的广播，它表示节点可以通过多条可选路径进行通信的程度，短路径比长路径贡献更大。尽管A和B到T的最短路径长度相同，但由于A到T的短路径更多，因此可沟通性预测RAT > RBT。c，网络通信测量与直接电刺激后经验观察到的反应幅度之间的相关性。诱发反应是根据解剖学上未连接部位间的颅内脑电图记录进行有创推断的。与最短路径效率相比，搜索信息和可交流性更能解释刺激传播的差异，从而让人们深入了解白质连通性的哪些特征决定了人脑中的多突触交流。图自参考文献116，Elsevier。


（六）术语表


复杂网络（Complex networks）
拓扑结构不复杂的网络，具有模块化结构、枢纽节点或小世界结构等特征。

连接体（Connectomes）
神经元之间的结构连接网络。根据神经元的空间尺度，连接可能从单个突触到大规模白质束不等。

分散系统（Decentralized systems）
单个神经元仅掌握网络组织局部知识的系统，与集中式系统形成鲜明对比。在集中式系统中，神经元或全局控制者可以鸟瞰整个网络。

延迟成本（Delay cost）
信号在网络中传输的效率。

扩散过程（Diffusion processes）
通过广播或随机游走动力学进行网络通信。

网络通信成本的维度（Dimensions of network communication cost）
可能形成连接体结构和神经信号机制的潜在进化压力。

能量成本（Energetic cost）
通过网络传输信号的代谢消耗
信息成本（Informational cost）
传播信号所需的网络拓扑知识量。

网络通信测量（Network communication measure）
在特定模型下量化通信特定属性的度量。

网络通信模型（Network communication models）
指导节点间通信的信号概念或传播算法。

网络拓扑结构（Network topology）
由相互连接元素组成的网络的组织特征。

神经元（Neural elements）
神经元可以是神经元、神经元群或宏观脑区，由神经网络中的节点表示。

参数模型（Parametric models）
通过路由和扩散相结合的混合策略进行网络通信。

多突触通信（Polysynaptic communication）
由一个或多个中间神经元介导的通信过程。

路由协议（Routing protocols）
通过选择性和高效路径进行网络通信。




5. 未来展望和建议




（一）支持相互竞争的大脑网络通信模型的现有证据综述


本文从(i)延迟、能量和信息成本的定性表现以及(ii)其解释力的实证证据这两个互补角度对网络通信模型进行了审视。根据这些标准可以得出结论：目前有哪些观点支持不同的连接组通信概念？

从概念的角度来看，可以按照从集中式（高效但依赖于强大的知识假设）到分散（假设薄弱但效率低下）传播政策的光谱来组织模型。本文推测，处于这一频谱两个极端的策略，即最短路径路由和无偏随机游走，不太可能反映神经信号的潜在机制，相反，以相互竞争的进化驱动力之间的平衡权衡为前提的模型和测量方法，可能会为连接组通信提供更符合生物学现实的描述，目前一系列神经科学领域的经验证据都支持这一观点。比较研究发现，搜索信息、可交流性和导航等指标通常能对经验现象做出最可靠的解释，虽然这些测量方法都属于通过扩散或路由进行交流的范畴，但它们并非纯粹基于最短路径或无偏随机游走。例如，导航旨在利用分散策略识别短路径，但不一定是最短路径。同样，搜索信息和可传播性描述的扩散过程虽然受到最短路径的影响，但也明显受到其他拓扑特征的影响。

这些观点强调，尽管最短路径路由作为通信模型有其局限性，但连接组的最短路径结构很可能在塑造神经信号方面发挥着重要作用。正如文中所探讨的，类似广播的策略，如可传播性和线性阈值模型，可以在不集中网络知识的情况下获取最短路径[81]。与此相关的是，最短路径测量仍然可以对网络属性进行有用的描述，因此可以用来描述连接组的组织特征，而不一定要提出关于神经通信的主张。

需要重申的是，迄今为止，测试和验证网络通信模型的系统性工作还很少，而且范围有限[39,49,116,124]，因此，关于比较相互竞争的模型的最佳方法，仍有许多问题有待解决。值得注意的是，目前还不清楚生物信号传递模式是否会因特定通信过程而有所不同，例如，内在功能同步化的信号机制与外源性脑刺激传播的信号机制是否相同[92]？同样，不同模型的效用是否会因个体临床特征（如认知受损、神经病理或受伤后的补偿和康复状态）而有所不同[29]？这些知识空白表明，本综述应通过今后在广泛神经科学领域的研究加以验证。最后，本文将讨论未来的机遇和实用建议，以指导网络通信模型的原则性开发、应用和验证。

（二）当前的局限性和未来的机遇


本节将讨论脑网络通信模型的局限性以及目前对这些模型进行审查的工作的局限性。首先，本文所提出的脑网络通信分类法只是组织文献中概念的一种可能方式，它只是绘制不同模型和测量方法间关系图的初步尝试，而非最终结论。此外，本文所考虑的通信成本的概念维度（延迟、信息和能量）过于简单化，很可能忽略了神经信号的重要方面。举例来说，它们没有考虑到信号保真度的问题，即在重新传输过程中信号完整性丢失的倾向[127,128]。

网络通信模型的前提条件是信号源和目标明确。尽管这种假设非常适合某些应用（例如，模拟外源扰动从刺激电极到记录电极的传播），但它仍然是对神经内在动力学的简化，值得在未来进行研究。同样，目前的模型假定所有节点对之间的通信都同等重要。除了导航（导航路径可能失效）外，其他模型允许所有节点对之间进行交互，然而，某些脑区在某些情况下可能并不打算进行交流，因此它们之间的信号传递可能会导致不适应的过度整合[129]。

同样，迄今为止的大多数研究都假定大脑网络中的所有节点都使用相同的策略进行交流，然而，当连接组嵌入了拓扑和三维空间，可能导致某些区域的策略有所偏好。例如，结构和功能模块内部与之间的信号交流可能采用不同的策略[130]，单模态与多模态皮层区域之间的交流也可能采用不同的策略[70,131]。最近的研究已开始探索这一问题，方法是建立复合模型，允许大脑区域使用不同的策略进行交流[132]。与此相关，直接模拟单个神经元内部计算的通信策略，如队列和碰撞模型，是未来研究的一个重要方向[128,133]。

目前网络通信模型的实例化并没有促进对时间分辨动力学的明确关注。通信矩阵是对神经信号的静态估计，不提供生成神经活动时间序列的方法，然而，通信测量可用于研究在不同时间尺度上展开的过程，例如电刺激的毫秒分辨率传播[116]、时变功能连接的波动[134,135]以及神经病理学随时间的扩散[104,106]。扩展本文综述的模型，更直接地纳入时间分辨的通信动力学是未来研究的一个很有前景的方向。

本文并未对文献中所有脑网络通信模型和测量方法都详尽调查，作者研究重点是极简模型，这些模型主要基于网络拓扑结构如何塑造信息流，不需要大量参数拟合（如果有的话）。除了所考虑的模型之外，还有许多其他模型已被应用于大脑网络值得进一步研究。例如，一些频谱模型[136-140]、流行病学模型[106,107,141]、信息论模型[127,142]、队列模型[133]和分组交换模型[143]。

更广义地说，网络通信工作是对其他大脑功能模型研究的补充，如网络控制理论[144]和神经动力学的生物物理模型[11]。前文回顾的许多应用研究也采用了这些方法，包括结构-功能耦合[145,146]、脑刺激[147-149]和病变影响[150]。每一类建模方法都为探究这些问题提供了互补的途径，它们在可解释性、计算效率和神经生物学保真度之间取得了不同的平衡。重要的是，已有研究开始探索整合这些模型领域的混合方法[151,152]，例如，最近开发的一个计算模型提出选择性使用结构连接的动态机制[153]，这为在神经系统生物物理模拟的背景下实施目前的通信策略铺平了道路。这一方向的研究有望开发和验证机理性、可解释性和可操作性强的大脑功能模型。

（三）关于应用和验证脑网络通信模型的建议


网络通信模型在神经科学各种研究中都有用武之地，然而迄今为止，人们仍不清楚哪种通信策略能最真实地描述生物神经信号。因此在过去的十年中，人们对量化连接组通信的兴趣与日俱增，促进了一系列网络测量方法的不断扩大。一方面，这种扩大使理论家们能够描述大脑组织和通讯的各种特性，另一方面，这也会让对网络测量作为一种研究工具感兴趣的从业人员望而生畏，并适得其反。本文认为，网络神经科学在理论和计算方面的进步必须与生物验证方面的实证密切配合。要实现这一目标，就必须将网络通信模型的原则性应用和生物学验证视为一枚硬币的两面。

首先，本文提倡研究考虑神经信号的多种概念化，以明确比较不同模式和测量方法产生的通信矩阵的解释力，重要的是，除了参与计算工作，实践者也能从这一建议中受益。正如我们所看到的，不同交流策略是以特定假设为前提的，这些假设涉及结构连通性如何介导神经元素之间的功能互动。因此，确定哪些网络测量方法能最准确、合理地解释经验观察结果，就能揭示相关现象背后的神经生物学过程。

其次，本文认为网络模型的生物学验证最终依赖于来自干预性或纵向实验设计的经验数据，例如，记录脑刺激的因果效应、神经退行性病变进展的纵向成像，以及评估脑损伤或连接中断后的结构和功能重构，这些现象提供了一个机会，将注意力从大脑网络的描述转移到机理和预后模型上来。其中许多课题的建模工作已经取得进展，未来工作应通过比较不同信号概念化的预测效用来推进。随着神经科学多个领域研究的进展，特定交流策略的证据可能会比现在更有说服力，从而缩小有用模型和测量方法的范围。

这些建议设想在网络神经科学的方法论和应用分支之间形成一个正反馈循环，其中建模的进步使从业人员能够更真实地描述大脑功能，而应用研究则指导新方法的验证和完善。最终，这种协同作用的目的是提供脑网络通信模型，以提供机理认识和临床实用性。希望本综述能为实现这一目标做出贡献。


参考文献

  1. Avena-Koenigsberger, A., Misic, B. & Sporns, O. Communication dynamics in complex brain networks. Nat. Rev. Neurosci. 19, 17–33 (2018).

    This Review was one of the first proposals of network communication as a conceptual framework to bridge the gap between brain structure and function.

  2. Laughlin, S. B. & Sejnowski, T. J. Communication in neuronal networks. Science 301, 1870–1874 (2003).

  3. Debanne, D., Bialowas, A. & Rama, S. What are the mechanisms for analogue and digital signalling in the brain? Nat. Rev. Neurosci. 14, 63–69 (2013).

  4. Hahn, G., Ponce-Alvarez, A., Deco, G., Aertsen, A. & Kumar, A. Portraits of communication in neuronal networks. Nat. Rev. Neurosci. 20, 117–127 (2019).

    This paper reviews putative mechanisms of communication in small networks of neuronal populations.

  5. Yeo, B. T. T. et al. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J. Neurophysiol. 106, 1125–1165 (2011).

  6. Kumar, A., Rotter, S. & Aertsen, A. Spiking activity propagation in neuronal networks: reconciling diferent perspectives on neural coding. Nat. Rev. Neurosci. 11, 615–627 (2010).

  7. Buzsáki, G. & Wang, X.-J. Mechanisms of gamma oscillations. Annu. Rev. Neurosci. 35, 203–225 (2012).

  8. Fries, P. Rhythms for cognition: communication through coherence. Neuron 88, 220–235 (2015).

  9. Kaufman, M. T., Churchland, M. M., Ryu, S. I. & Shenoy, K. V. Cortical activity in the null space: permitting preparation without movement. Nat. Neurosci. 17, 440–448 (2014).

  10. Semedo, J. D., Zandvakili, A., Machens, C. K., Yu, B. M. & Kohn, A. Cortical areas interact through a communication subspace. Neuron 102, 249–259.e4 (2019).

  11. Deco, G., Jirsa, V. K., Robinson, P. A., Breakspear, M. & Friston, K. The dynamic brain: from spiking neurons to neural masses and cortical fields. PLoS Comput. Biol. 4, e1000092 (2008).

  12. Palmigiano, A., Geisel, T., Wolf, F. & Battaglia, D. Flexible information routing by transient synchrony. Nat. Neurosci. 20, 1014–1022 (2017).

  13. Bassett, D. S. & Sporns, O. Network neuroscience. Nat. Neurosci. 20, 353–364 (2017).

  14. Bullmore, E. & Sporns, O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 10, 186–198 (2009).

  15. Fornito, A., Zalesky, A. & Bullmore, E. T. Fundamentals of Brain Network Analysis(Academic, 2016).

    This book provides a comprehensive introduction to network neuroscience and connectomics.

  16. Javadzadeh, M. & Hofer, S. B. Dynamic causal communication channels between neocortical areas. Neuron 110, 2470–2483.e7 (2022).

  17. Park, H.-J. & Friston, K. Structural and functional brain networks: from connections to cognition. Science 342, 1238411 (2013).

  18. Suárez, L. E., Markello, R. D., Betzel, R. F. & Misic, B. Linking structure and function in macroscale brain networks. Trends Cogn. Sci. 24, 302–315 (2020).

  19. Hagmann, P. et al. Mapping the structural core of human cerebral cortex. PLoS Biol. 6, e159 (2008).

  20. van den Heuvel, M. P. & Sporns, O. Rich-club organization of the human connectome. J. Neurosci. 31, 15775–15786 (2011).

  21. Meunier, D., Lambiotte, R. & Bullmore, E. T. Modular and hierarchically modular organization of brain networks. Front. Neurosci. 4, 200 (2010).

  22. Bassett, D. S. & Bullmore, E. Small-world brain networks. Neuroscientist 12, 512–523 (2006).

  23. van den Heuvel, M. P., Bullmore, E. T. & Sporns, O. Comparative connectomics. Trends Cogn. Sci. 20, 345–361 (2016).

  24. Bullmore, E. & Sporns, O. The economy of brain network organization. Nat. Rev. Neurosci.13, 336–349 (2012).

  25. van den Heuvel, M. P., Kahn, R. S., Goñi, J. & Sporns, O. High-cost, high-capacity backbone for global brain communication. Proc. Natl Acad. Sci. USA 109, 11372–11377 (2012).

  26. Cole, M. W., Ito, T., Bassett, D. S. & Schultz, D. H. Activity flow over resting-state networks shapes cognitive task activations. Nat. Neurosci. 19, 1718–1726 (2016).

  27. Shine, J. M. et al. Human cognition involves the dynamic integration of neural activity and neuromodulatory systems. Nat. Neurosci. 22, 289–296 (2019).

  28. van den Heuvel, M. P. & Sporns, O. A cross-disorder connectome landscape of brain dysconnectivity. Nat. Rev. Neurosci. 20, 435–446 (2019).

  29. Fornito, A., Zalesky, A. & Breakspear, M. The connectomics of brain disorders. Nat. Rev. Neurosci. 16, 159–172 (2015).

  30. Stam, C. J. Modern network science of neurological disorders. Nat. Rev. Neurosci. 15, 683–695 (2014).

  31. Achard, S., Salvador, R., Whitcher, B., Suckling, J. & Bullmore, E. A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J. Neurosci. 26, 63–72 (2006).

  32. Watts, D. J. & Strogatz, S. H. Collective dynamics of ‘small-world’ networks. Nature 393, 440–442 (1998).

  33. Kaiser, M. & Hilgetag, C. C. Nonoptimal component placement, but short processing paths, due to long-distance projections in neural systems. PLoS Comput. Biol. 2, e95 (2006).

  34. Zamora-López, G., Zhou, C. & Kurths, J. Cortical hubs form a module for multisensory integration on top of the hierarchy of cortical networks. Front. Neuroinform. 4, 1 (2010).

  35. Papo, D., Zanin, M., Martínez, J. H. & Buldú, J. M. Beware of the small-world neuroscientist! Front. Hum. Neurosci. 10, 96 (2016).

  36. Rubinov, M. & Sporns, O. Complex network measures of brain connectivity: uses and interpretations. NeuroImage 52, 1059–1069 (2010).

  37. Varshney, L. R., Chen, B. L., Paniagua, E., Hall, D. H. & Chklovskii, D. B. Structural properties of the Caenorhabditis elegans neuronal network. PLoS Comput. Biol. 7, e1001066 (2011).

  38. Grifa, A., Baumann, P. S., Thiran, J.-P. & Hagmann, P. Structural connectomics in brain diseases. NeuroImage 80, 515–526 (2013).

  39. Goñi, J. et al. Resting-brain functional connectivity predicted by analytic measures of network communication. Proc. Natl Acad. Sci. USA 111, 833–838 (2014).

    This work was one of the first empirical demonstrations that network communication models can be used to infer functional connectivity from brain network structure.

  40. Avena-Koenigsberger, A. et al. Path ensembles and a tradeof between communication eficiency and resilience in the human connectome. Brain Struct. Funct. 222, 603–618 (2016).

  41. Seguin, C., van den Heuvel, M. P. & Zalesky, A. Navigation of brain networks. Proc. Natl Acad. Sci. USA 115, 6297–6302 (2018).

    This study was the first comprehensive exploration of the network navigation model in neuroscience.

  42. Kleinberg, J. M. Navigation in a small world. Nature 406, 845 (2000).

  43. Boguna, M., Krioukov, D. & Clafy, K. C. Navigability of complex networks. Nat. Phys. 5, 74–80 (2009).

  44. Goñi, J. et al. Exploring the morphospace of communication eficiency in complex networks. PLoS One 8, e58070 (2013).

  45. Travers, J. & Milgram, S. An experimental study of the small world problem. Sociometry32, 425–443 (1969).

    A prescient and highly influential account of decentralized communication in complex networks.

  46. Boguñá, M., Papadopoulos, F. & Krioukov, D. Sustaining the Internet with hyperbolic mapping. Nat. Commun. 1, 62 (2010).

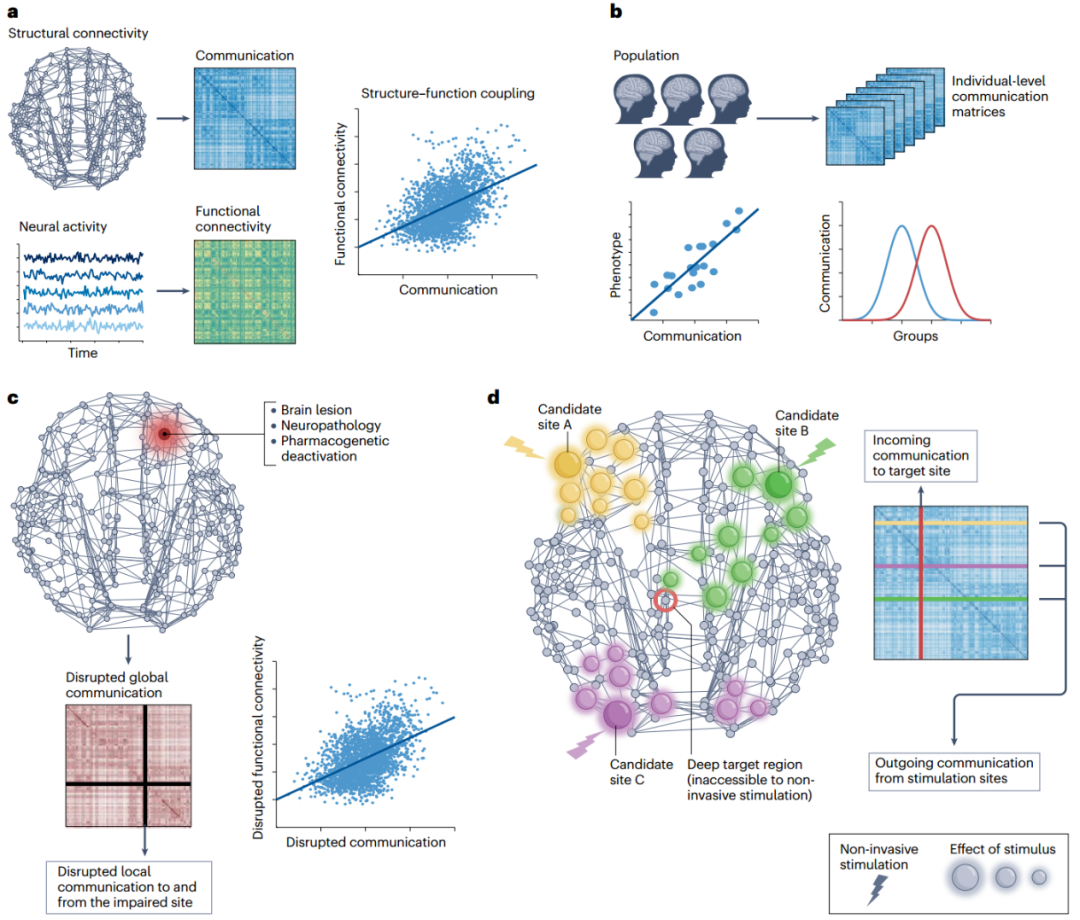
  47. Grayson, D. S. et al. The rhesus monkey connectome predicts disrupted functional networks resulting from pharmacogenetic inactivation of the amygdala. Neuron 91, 453–466 (2016).

    This paper shows that network communication models can predict global changes in functional connectivity resulting from the deactivation of targeted regions.

  48. Betzel, R. F. et al. Structural, geometric and genetic factors predict interregional brain connectivity patterns probed by electrocorticography. Nat. Biomed. Eng. 3, 902–916 (2019).

  49. Seguin, C., Tian, Y. & Zalesky, A. Network communication models improve the behavioral and functional predictive utility of the human structural connectome. Netw. Neurosci. 4, 980–1006 (2020).

  50. Imms, P. et al. Navigating the link between processing speed and network communication in the human brain. Brain Struct. Funct. 226, 1281–1302 (2021).

  51. de Lange, S. C. et al. Shared vulnerability for connectome alterations across psychiatric and neurological brain disorders. Nat. Hum. Behav. 3, 988–998 (2019).

    This paper uses a large sample of patients to identify a cross-disorder basis for disrupted brain network communication in neuropsychiatric conditions.

  52. Lella, E. & Estrada, E. Communicability distance reveals hidden patterns of Alzheimer’s disease. Netw. Neurosci. 4, 1007–1029 (2020).

  53. Wang, X. et al. Synchronization lag in post stroke: relation to motor function and structural connectivity. Netw. Neurosci. 3, 1121–1140 (2019).

  54. Hermundstad, A. M. et al. Structural foundations of resting-state and task-based functional connectivity in the human brain. Proc. Natl Acad. Sci. USA 110, 6169–6174 (2013).

  55. Cook, S. J. et al. Whole-animal connectomes of both Caenorhabditis elegans sexes. Nature 571, 63–71 (2019).

  56. Winding, M. et al. The connectome of an insect brain. Science 379, eadd9330 (2023).

    This recent paper was the first to investigate polysynaptic streams of information flow in a complete insect connectome.

  57. Alves, P. N. et al. An improved neuroanatomical model of the default-mode network reconciles previous neuroimaging and neuropathological findings. Commun. Biol. 2, 370 (2019).

  58. Uddin, L. Q. et al. Residual functional connectivity in the split-brain revealed with resting-state functional MRI. Neuroreport 19, 703–709 (2008).

  59. Trebaul, L. et al. Probabilistic functional tractography of the human cortex revisited. Neuroimage 181, 414–429 (2018).

  60. Momi, D., Wang, Z. & Grifiths, J. D. TMS-evoked responses are driven by recurrent large-scale network dynamics. eLife 12, e83232 (2023).

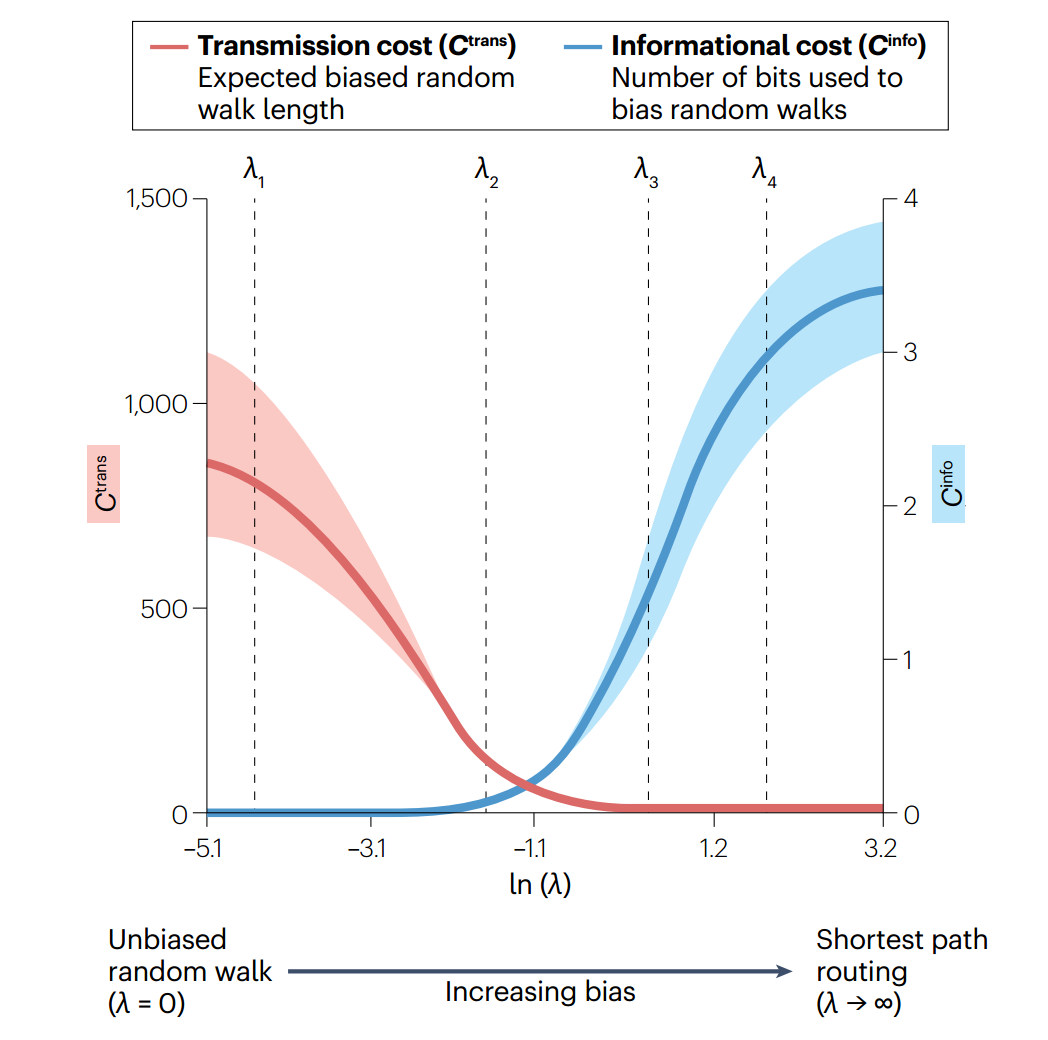
  61. Laughlin, S. B., de Ruyter van Steveninck, R. R. & Anderson, J. C. The metabolic cost of neural information. Nat. Neurosci. 1, 36–41 (1998).

  62. Avena-Koenigsberger, A. et al. A spectrum of routing strategies for brain networks. PLoS Comput. Biol. 15, e1006833 (2019).

    This work presents one of the first applications of the biased random walk model in network neuroscience.

  63. Avena-Koenigsberger, A. et al. Using Pareto optimality to explore the topology and dynamics of the human connectome. Philos. Trans. R. Soc. Lond. B Biol. Sci. 369, 20130530 (2014).

  64. Avena-Koenigsberger, A., Goñi, J., Solé, R. & Sporns, O. Network morphospace. J. R. Soc. Interface 12, 20140881 (2015).

  65. Serrano, M. A., Krioukov, D. & Boguñá, M. Self-similarity of complex networks and hidden metric spaces. Phys. Rev. Lett. 100, 078701 (2008).

  66. Kleinberg, J. Complex networks and decentralized search algorithms. Proc. Int. Congr. Math. 3, 1019–1044 (2006).

  67. Cannistraci, C. V. & Muscoloni, A. Geometrical congruence, greedy navigability and myopic transfer in complex networks and brain connectomes. Nat. Commun. 13, 7308 (2022).

  68. Roberts, J. A. et al. The contribution of geometry to the human connectome. NeuroImage124, 379–393 (2016).

  69. Stiso, J. & Bassett, D. S. Spatial embedding imposes constraints on neuronal network architectures. Trends Cogn. Sci. 22, 1127–1142 (2018).

  70. Vézquez-Rodríguez, B., Liu, Z.-Q., Hagmann, P. & Misic, B. Signal propagation via cortical hierarchies. Netw. Neurosci. 4, 1072–1090 (2020).

  71. Boguñá, M. et al. Network geometry. Nat. Rev. Phys. 3, 114–135 (2021).

  72. Zheng, M., Allard, A., Hagmann, P., Alemán-Gómez, Y. & Serrano, M. Á. Geometric renormalization unravels self-similarity of the multiscale human connectome. Proc.Natl Acad. Sci. USA 117, 20244–20253 (2020).

  73. Allard, A. & Serrano, M. Á. Navigable maps of structural brain networks across species. PLoS Comput. Biol. 16, e1007584 (2020).

  74. Duran-Nebreda, S., Johnston, I. G. & Bassel, G. W. Eficient vasculature investment in tissues can be determined without global information. J. R. Soc. Interface 17, 20200137 (2020).

  75. Masuda, N., Porter, M. A. & Lambiotte, R. Random walks and difusion on networks. Phys. Rep. 716, 1–58 (2017).

    This study is a comprehensive review on random walks dynamics in complex networks.

  76. Noh, J. D. & Rieger, H. Random walks on complex networks. Phys. Rev. Lett. 92, 118701 (2004).

  77. Estrada, E. & Hatano, N. Communicability in complex networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 77, 036111 (2008)

    This seminal work introduced the concept of communicability in complex networks.

  78. Estrada, E., Hatano, N. & Benzi, M. The physics of communicability in complex networks. Phys. Rep. 514, 89–119 (2012).

  79. Granovetter, M. Threshold models of collective behavior. Am. J. Sociol. 83, 1420–1443 (1978).

  80. Nematzadeh, A., Ferrara, E., Flammini, A. & Ahn, Y.-Y. Optimal network modularity for information difusion. Phys. Rev. Lett. 113, 088701 (2014).

  81. Mišić, B. et al. Cooperative and competitive spreading dynamics on the human connectome. Neuron 86, 1518–1529 (2015).

  82. Worrell, J. C., Rumschlag, J., Betzel, R. F., Sporns, O. & Mišić, B. Optimized connectome architecture for sensory-motor integration. Netw. Neurosci. 1, 415–430 (2018).

  83. Shadi, K., Dyer, E. & Dovrolis, C. Multisensory integration in the mouse cortical connectome using a network difusion model. Netw. Neurosci. 4, 1030–1054 (2020).

  84. Gómez-Gardeñes, J. & Latora, V. Entropy rate of difusion processes on complex networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 78, 065102 (2008).

  85. Lambiotte, R. et al. Flow graphs: interweaving dynamics and structure. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 84, 017102 (2011).

  86. Benigni, B., Gallotti, R. & De Domenico, M. Potential-driven random walks on interconnected systems. Phys. Rev. E 104, 024120 (2021).

  87. Yin, C.-Y., Wang, B.-H., Wang, W.-X., Zhou, T. & Yang, H.-J. Eficient routing on scale-free networks based on local information. Phys. Lett. A 351, 220–224 (2006).

  88. Csoma, A. et al. Routes obey hierarchy in complex networks. Sci. Rep. 7, 7243 (2017).

  89. Deco, G., Jirsa, V. K. & McIntosh, A. R. Emerging concepts for the dynamical organization of resting-state activity in the brain. Nat. Rev. Neurosci. 12, 43–56 (2011).

  90. Abdelnour, F., Voss, H. U. & Raj, A. Network difusion accurately models the relationship between structural and functional brain connectivity networks. NeuroImage 90, 335–347 (2014).

  91. Cole, M. W., Bassett, D. S., Power, J. D., Braver, T. S. & Petersen, S. E. Intrinsic and task-evoked network architectures of the human brain. Neuron 83, 238–251 (2014).

  92. Siddiqi, S. H., Kording, K. P., Parvizi, J. & Fox, M. D. Causal mapping of human brain function. Nat. Rev. Neurosci. 23, 361–375 (2022).

    This recent review discusses current eforts and future directions to map causal interactions in the human brain. Concepts outlined in this work may provide avenues for the testing and validation of network communication models.

  93. Medaglia, J. D., Lynall, M.-E. & Bassett, D. S. Cognitive network neuroscience. J. Cogn. Neurosci. 27, 1471–1491 (2015).

  94. Smith, S. M. et al. A positive–negative mode of population covariation links brain connectivity, demographics and behavior. Nat. Neurosci. 18, 1565–1567 (2015).

  95. Fornito, A., Zalesky, A. & Breakspear, M. Graph analysis of the human connectome: promise, progress, and pitfalls. NeuroImage 80, 426–444 (2013).

  96. Popp, J. L. et al. Structural–functional brain network coupling predicts human cognitive ability. Preprint at bioRxiv https://doi.org/10.1101/2023.02.09.527639 (2023).

  97. Zorlu, N. et al. Abnormal structural network communication reflects cognitive deficits in schizophrenia. Brain Topogr. 36, 294–304 (2023).

  98. Imms, P. et al. The structural connectome in traumatic brain injury: a meta-analysis of graph metrics. Neurosci. Biobehav. Rev. 99, 128–137 (2019)

  99. Imms, P. et al. Exploring personalized structural connectomics for moderate to severe traumatic brain injury. Netw. Neurosci. 7, 160–183 (2023).

  100. Kuceyeski, A. et al. The application of a mathematical model linking structural and functional connectomes in severe brain injury. NeuroImage Clin. 11, 635–647 (2016).

  101. Kuceyeski, A. F., Jamison, K. W., Owen, J. P., Raj, A. & Mukherjee, P. Longitudinal increases in structural connectome segregation and functional connectome integration are associated with better recovery after mild TBI. Hum. Brain Mapp. 40, 4441–4456 (2019).

  102. Albert, R., Jeong, H. & Barabasi, A. L. Error and attack tolerance of complex networks. Nature 406, 378–382 (2000).

  103. Palop, J. J. & Mucke, L. Amyloid-beta-induced neuronal dysfunction in Alzheimer’s disease: from synapses toward neural networks. Nat. Neurosci. 13, 812–818 (2010).

  104. Raj, A., Kuceyeski, A. & Weiner, M. A network difusion model of disease progression in dementia. Neuron 73, 1204–1215 (2012).

  105. Meier, J. M. et al. Connectome-based propagation model in amyotrophic lateral sclerosis. Ann. Neurol. 87, 725–738 (2020).

  106. Vogel, J. W. et al. Spread of pathological tau proteins through communicating neurons in human Alzheimer’s disease. Nat. Commun. 11, 2612 (2020).

  107. Zheng, Y.-Q. et al. Local vulnerability and global connectivity jointly shape neurodegenerative disease propagation. PLoS Biol. 17, e3000495 (2019).

  108. Wannan, C. M. J. et al. Evidence for network-based cortical thickness reductions in schizophrenia. Am. J. Psychiatry 176, 552–563 (2019).

  109. Shafiei, G. et al. Spatial patterning of tissue volume loss in schizophrenia reflects brain network architecture. Biol. Psychiatry 87, 727–735 (2020).

  110. Miller, K. L. et al. Multimodal population brain imaging in the UK Biobank prospective epidemiological study. Nat. Neurosci. 19, 1523–1536 (2016).

  111. Sina Mansour, L., Di Biase, M. A., Smith, R. E., Zalesky, A. & Seguin, C. Connectomes for 40,000 UK Biobank participants: a multi-modal, multi-scale brain network resource. Preprint at bioRxiv https://doi.org/10.1101/2023.03.10.532036 (2023).

  112. Keller, C. J. et al. Mapping human brain networks with cortico-cortical evoked potentials. Philos. Trans. R. Soc. Lond. B Biol. Sci. 369, 20130528 (2014).

  113. Sydnor, V. J. et al. Cortical–subcortical structural connections support transcranial magnetic stimulation engagement of the amygdala. Sci. Adv. 8, eabn5803 (2022).

  114. Ozdemir, R. A. et al. Individualized perturbation of the human connectome reveals reproducible biomarkers of network dynamics relevant to cognition. Proc. Natl Acad. Sci. USA 117, 8115–8125 (2020).

  115. Veit, M. J. et al. Temporal order of signal propagation within and across intrinsic brain networks. Proc. Natl Acad. Sci. USA 118, e2105031118 (2021).

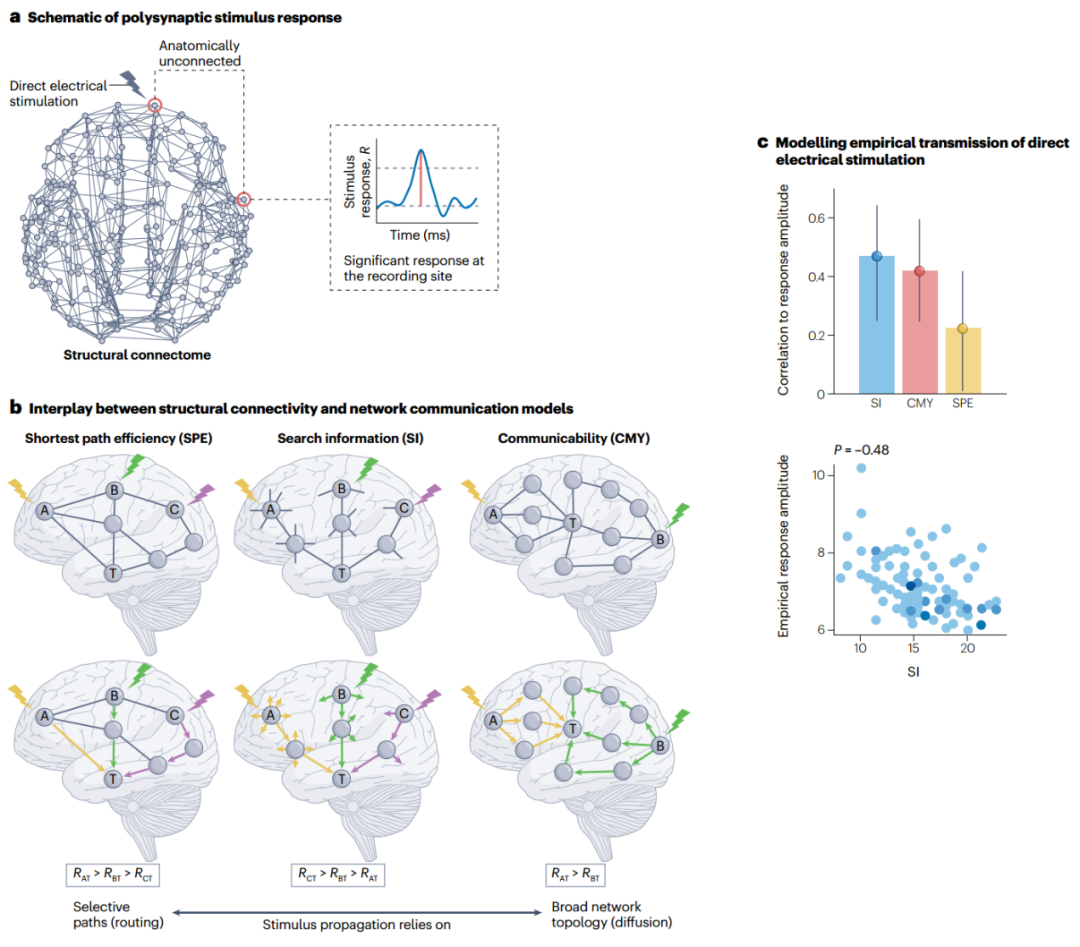
  116. Seguin, C. et al. Communication dynamics in the human connectome shape the cortex-wide propagation of direct electrical stimulation. Neuron 111, 1391–1401.e5 (2023).

    The first paper to show that network communication models can predict the propagation of direct electrical stimulation through the human brain.

  117. Siddiqi, S. H., Taylor, J. J., Horn, A. & Fox, M. D. Bringing human brain connectomics to clinical practice in psychiatry. Biol. Psychiatry 93, 386–387 (2023).

  118. Horn, A. & Fox, M. D. Opportunities of connectomic neuromodulation. NeuroImage 221, 117180 (2020).

  119. Horn, A. et al. Connectivity predicts deep brain stimulation outcome in Parkinson disease. Ann. Neurol. 82, 67–78 (2017).

  120. Cash, R. F. H. et al. Subgenual functional connectivity predicts antidepressant treatment response to transcranial magnetic stimulation: independent validation and evaluation of personalization. Biol. Psychiatry 86, e5–e7 (2019).

  121. Fox, M. D., Buckner, R. L., White, M. P., Greicius, M. D. & Pascual-Leone, A. Eficacy of transcranial magnetic stimulation targets for depression is related to intrinsic functional connectivity with the subgenual cingulate. Biol. Psychiatry 72, 595–603 (2012).

  122. Schelling, T. C. Dynamic models of segregation. J. Math. Sociol. 1, 143–186 (1971).

  123. Helbing, D., Farkas, I. & Vicsek, T. Simulating dynamical features of escape panic. Nature407, 487–490 (2000).

  124. Zamani Esfahlani, F., Faskowitz, J., Slack, J., Mišić, B. & Betzel, R. F. Local structure–function relationships in human brain networks across the lifespan. Nat. Commun. 13, 2053 (2022).

    This paper carries out a comprehensive comparison of the extent to which diferent network communication models can explain patterns of functional connectivity.

  125. Mišic, B. et al. Network-based asymmetry of the human auditory system. Cereb. Cortex28, 2655–2664 (2018).

  126. Seguin, C., Mansour, C. S., Sporns, O., Zalesky, A. & Calamante, F. Network communication models narrow the gap between the modular organization of structural and functional brain networks. NeuroImage 257, 119323 (2022).

  127. Amico, E. et al. Toward an information theoretical description of communication in brain networks. Netw. Neurosci. 5, 646–665 (2021).

  128. Hao, Y. & Graham, D. Creative destruction: sparse activity emerges on the mammal connectome under a simulated communication strategy with collisions and redundancy. Netw. Neurosci. 4, 1055–1071 (2020).

  129. Hillary, F. G. & Grafman, J. H. Injured brains and adaptive networks: the benefits and costs of hyperconnectivity. Trends Cogn. Sci. 21, 385–401 (2017).

  130. Park, B.-Y. et al. Signal difusion along connectome gradients and inter-hub routing diferentially contribute to dynamic human brain function. NeuroImage 224, 117429 (2021).

  131. Bazinet, V., Vos de Wael, R., Hagmann, P., Bernhardt, B. C. & Misic, B. Multiscale communication in cortico-cortical networks. NeuroImage 243, 118546 (2021).

  132. Betzel, R. F., Faskowitz, J., Mišić, B., Sporns, O. & Seguin, C. Multi-policy models of interregional communication in the human connectome. Preprint at bioRxiv https://doi.org/10.1101/2022.05.08.490752 (2022).

  133. Mišić, B., Sporns, O. & McIntosh, A. R. Communication eficiency and congestion of signal trafic in large-scale brain networks. PLoS Comput. Biol. 10, e1003427 (2014).

  134. Grifa, A. et al. Transient networks of spatio-temporal connectivity map communication pathways in brain functional systems. NeuroImage 155, 490–502 (2017).

    This work uses an innovative multilayer framework to track the time-resolved propagation of functional activity and relates it to communication via structural connectivity.

  135. Liu, Z.-Q. et al. Time-resolved structure–function coupling in brain networks. Commun. Biol. 5, 532 (2022).

  136. de Lange, S. C., de Reus, M. A. & van den Heuvel, M. P. The Laplacian spectrum of neural networks. Front. Comput. Neurosci. 7, 189 (2014).

  137. Becker, C. O. et al. Spectral mapping of brain functional connectivity from difusion imaging. Sci. Rep. 8, 1411 (2018).

  138. Abdelnour, F., Dayan, M., Devinsky, O., Thesen, T. & Raj, A. Functional brain connectivity is predictable from anatomic network’s Laplacian eigen-structure. NeuroImage 172, 728–739 (2018).

  139. Deslauriers-Gauthier, S., Zucchelli, M., Frigo, M. & Deriche, R. A unified framework for multimodal structure–function mapping based on eigenmodes. Med. Image Anal. 66, 101799 (2020).

  140. Tewarie, P. et al. Mapping functional brain networks from the structural connectome: relating the series expansion and eigenmode approaches. NeuroImage 216, 116805 (2020).

  141. Meier, J. et al. The epidemic spreading model and the direction of information flow in brain networks. NeuroImage 152, 639–646 (2017).

  142. Benigni, B., Ghavasieh, A., Corso, A., d’Andrea, V. & De Domenico, M. Persistence of information flow: a multiscale characterization of human brain. Netw. Neurosci. 5, 831–850 (2021).

  143. Graham, D. & Rockmore, D. The packet switching brain. J. Cogn. Neurosci. 23, 267–276 (2011).

  144. Betzel, R. F., Gu, S., Medaglia, J. D., Pasqualetti, F. & Bassett, D. S. Optimally controlling the human connectome: the role of network topology. Sci. Rep. 6, 30770 (2016).

  145. Deco, G. et al. Resting-state functional connectivity emerges from structurally and dynamically shaped slow linear fluctuations. J. Neurosci. 33, 11239–11252 (2013).

  146. Honey, C. J. et al. Predicting human resting-state functional connectivity from structural connectivity. Proc. Natl Acad. Sci. USA 106, 2035–2040 (2009).

  147. Muldoon, S. F. et al. Stimulation-based control of dynamic brain networks. PLoS Comput. Biol. 12, e1005076 (2016).

  148. Gollo, L. L., Roberts, J. A. & Cocchi, L. Mapping how local perturbations influence systems-level brain dynamics. NeuroImage 160, 97–112 (2017).

  149. Stiso, J. et al. White matter network architecture guides direct electrical stimulation through optimal state transitions. 2018 Conference on Cognitive Computational Neuroscience. https://doi.org/10.32470/ccn.2018.1028-0 (2018).

  150. Aerts, H., Fias, W., Caeyenberghs, K. & Marinazzo, D. Brain networks under attack: robustness properties and the impact of lesions. Brain 139, 3063–3083 (2016).

  151. Srivastava, P. et al. Models of communication and control for brain networks: distinctions, convergence, and future outlook. Netw. Neurosci. 4, 1122–1159 (2020).

    A recent review highlighting opportunities for synergy between diferent computational avenues to model brain function, including network communication, dynamical systems and control theory.

  152. Finger, H., Gast, R., Gerlof, C., Engel, A. K. & König, P. Probing neural networks for dynamic switches of communication pathways. PLOS Comput. Biol. 15, e1007551 (2019).

  153. Pope, M., Seguin, C., Varley, T. F., Faskowitz, J. & Sporns, O. Co-evolving dynamics and topology in a coupled oscillator model of resting brain function. Preprint at bioRxivhttps://doi.org/10.1101/2023.01.31.526514 (2023).

  154. Osmanlıoğlu, Y. et al. System-level matching of structural and functional connectomes in the human brain. Neuroimage 199, 93–104 (2019).

  155. Seguin, C., Razi, A. & Zalesky, A. Inferring neural signalling directionality from undirected structural connectomes. Nat. Commun. 10, 4289 (2019).

  156. Vázquez-Rodríguez, B. et al. Gradients of structure–function tethering across neocortex. Proc. Natl Acad. Sci. USA 116, 21219–21227 (2019).

  157. Tewarie, P. et al. Predicting time‐resolved electrophysiological brain networks from structural eigenmodes. Hum. Brain Mapp. 43, 4475–4491 (2022).

  158. Nakuci, J., McGuire, M., Schweser, F., Poulsen, D. & Muldoon, S. F. Diferential patterns of change in brain connectivity resulting from severe traumatic brain injury. Brain Connect.12, 799–811 (2022).

  159. Li, Y. et al. Difusion tensor imaging based network analysis detects alterations of neuroconnectivity in patients with clinically early relapsing-remitting multiple sclerosis. Hum. Brain Mapp. 34, 3376–3391 (2013).

  160. Crofts, J. J. et al. Network analysis detects changes in the contralesional hemisphere following stroke. NeuroImage 54, 161–169 (2011).

  161. Andreotti, J. et al. Validation of network communicability metrics for the analysis of brain structural networks. PLoS One 9, e115503 (2014).

  162. Latora, V. & Marchiori, M. Eficient behavior of small-world networks. Phys. Rev. Lett. 87, 198701 (2001).

  163. Muscoloni, A., Thomas, J. M., Ciucci, S., Bianconi, G. & Cannistraci, C. V. Machine learning meets complex networks via coalescent embedding in the hyperbolic space. Nat. Commun. 8, 1615 (2017).

  164. Rosvall, M., Grönlund, A., Minnhagen, P. & Sneppen, K. Searchability of networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 72, 046117 (2005).

    This paper first proposed the concept of search information and applied it to complex networks.

  165. Sneppen, K., Trusina, A. & Rosvall, M. Hide-and-seek on complex networks. Europhys. Lett. 69, 853–859 (2005).

  166. Kaiser, M., Görner, M. & Hilgetag, C. C. Criticality of spreading dynamics in hierarchical cluster networks without inhibition. N. J. Phys. 9, 110 (2007).

  167. Pei, S. & Makse, H. A. Spreading dynamics in complex networks. J. Stat. Mech. Theory Exp. 2013, P12002 (2013).

  168. Wook Yoo, S. et al. A network flow-based analysis of cognitive reserve in normal ageing and Alzheimer’s disease. Sci. Rep. 5, 10057 (2015).

  169. Kaiser, M., Martin, R., Andras, P. & Young, M. P. Simulation of robustness against lesions of cortical networks. Eur. J. Neurosci. 25, 3185–3192 (2007).

（参考文献可上下滑动查看）



神经动力学模型读书会


为了促进神经科学、系统科学以及计算机科学等多领域学术工作者的交流合作，吸引更多朋友共同探索脑科学与类脑研究，周昌松、臧蕴亮、杨冬平、郭大庆、陈育涵、曹淼、刘泉影、王大辉、刘健、王鑫迪等来自国内外多所知名高校的专家学者在集智俱乐部共同发起「神经动力学模型」读书会，历时四个月研讨，近日圆满结束。


本季读书会形成了聚集500+成员的神经动力学社区，积累了40+小时综述、解读、研讨的视频记录，以及多篇社区成员总结的词条、笔记、翻译、科普资料等。现在报名加入读书会，即可加入社区交流讨论（微信），并解锁相关视频、文本资料。我们对脑的探索才刚刚起航，欢迎你一道参与，共同点亮更多脑科学研究的岛屿！




详情请见：

500+神经动力学社区成员，邀你共同点亮更多脑科学研究的岛屿



高阶网络社区


随着对现实世界探索的不断深入，人们发现在许多真实的复杂系统中，组成系统的个体之间不仅存在二元交互关系，也广泛存在多个体同时（或以特定顺序）进行交互，即高阶交互现象。为此，研究人员分别发展出了基于超图、单纯复形、依赖关系等的网络高阶表示模型，为复杂网络分析和研究提供了新的思路。


由电子科技大学吕琳媛老师、任晓龙老师及中国地质大学（北京）管青老师在集智俱乐部联合发起了【高阶网络读书会】。读书会围绕高阶交互网络的基本概念、模型、方法与应用等研究进行研讨，按照「基础理论」+「深入理论」+「案例研讨」的模式展开。读书会第一季已经圆满结束，第二季正在筹备中。现在报名加入可以解锁第一季全部录播视频并加入社群交流。


详情请见：

探索复杂系统高阶交互的奥秘 | 高阶网络读书会启动



推荐阅读

‍1. 经典综述：大尺度脑活动的动力学模型
2. 长文综述：大脑中的熵、自由能、对称性和动力学
3. Nat. Commun.长文综述：具身神经形态智能
4. 张江：第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程
5. 加入集智学园VIP，获得20周年“涌现”学术年会入场券！
6. 加入集智，一起复杂！


点击“阅读原文”，报名读书会