关键词：量子临界性，量子纠缠，临界动力学，矩阵乘积态，标度坍缩



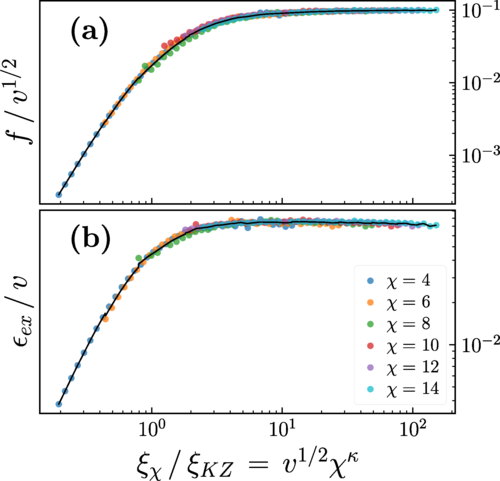
论文题目：
Universality of Critical Dynamics with Finite Entanglement
论文地址：
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.131.106501

当系统穿越量子临界点时，量子 Kibble-Zurek 机制可以对产生的激发能量数量等提供普适预测。现在，这一机制被用于在新兴的量子计算机和仿真器上获得临界指数，这在某些情况下可以与矩阵乘积态（MPS）的数值研究进行比较。然而，当实验或经典计算没有完全捕获用于忠实描述许多量子临界点所需的纠缠熵散度时，这一机制会被修改。

这项工作研究了量子系统在临界点附近的低能动力学如何被有限纠缠（Finite Entanglement）所改变，以由矩阵乘积态近似描述的共形不变临界点为例。研究得出的结论是，有限纠缠对 Kibble-Zurek 过程的影响，可以由两个长度尺度之比的无量纲标度函数捕获，其中一个动态地确定，另一个由纠缠限制确定。

研究首先在数值上确认了在有限键合维度 χ 下的动力学与所选择的算法无关，然后获得了在横向场伊辛模型和三态波茨模型中进行的扫描的标度坍缩（scaling collapse）。这些结果明确了纠缠在时间相关的临界现象中所起的确切作用，并对量子态制备和量子态的经典模拟产生直接影响。

图1. 一次 Kibble-Zurek 扫描之后的激发能量密度

图2. 标度函数坍缩


编译｜梁金

集智量子交流群


量子力学作为现代物理学的两大核心理论之一，成功描述了微观物理体系的演化规律。量子概念的引入深刻地揭示了一系列与宏观体系截然不同的物理机制，在近年来逐渐发展出了包含量子通信、量子计算、量子模拟、量子测量等量子信息科学的全新研究领域和方向。


我们感受到以量子力学为基础的革命是颠覆性的，也将影响到未来的复杂性科学研究。集智社区中已经有一些从事量子相关研究工作的活跃社区成员，我们建立了一个集智的量子相关交流群，欢迎你加入交流。


扫描以下二维码，填写个人信息，加入「集智量子交流群」



推荐阅读

‍1. PRX 速递：量子多体动力学的统一理论——本征算子热化定理
2. PRL 速递：宽量子神经网络动力学的分析理论
3. 具有张量网络的强化学习进行自纠错量子多体控制｜Nat. Mach. Intell. 速递
4. 张江：第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程
5. 成为集智VIP，解锁全站课程／读书会
6. 加入集智，一起复杂！


点击“阅读原文”，加入集智量子交流群