James Crutchfield 1983年博士毕业于加州大学圣克鲁兹分校,1990-2004年在圣塔菲研究所工作,现为加州大学戴维斯分校物理系教授,研究兴趣包括非线性动力学,凝聚态物理,计算物理学,演化动力学,斑图发现等等。
学者主页:https://csc.ucdavis.edu/~chaos/
James Crutchfield 是一名混沌物理学家。混沌是一种演化规则确定,但未来却不可预测的神奇现象。他有一次发现基于香农熵的信息论可以用来对混沌动力学的未来预测做度量,从此踏上了从信息论视角研究复杂系统的道路,并因此发展出计算力学这一框架。他的工作非常关注模型对确定性和随机性的划分。确定的动力学会涌现出随机的不可预测的混沌现象,而有些随机动力学却可以找到宏观的确定规律,如果我们把确定性和随机性的视角结合起来,能否解开涌现的谜团呢?
这是 James Crutchfield 二十多年来致力回答的问题。计算力学研究发展至今已经有很多相关论文了,而《The Calculi of Emergence: Computation, Dynamics, and Induction》这篇论文较为系统地梳理了计算力学的发展脉络。接下来我们主要介绍这篇文章的内容。
Crutchfield, James P. “The calculi of emergence: computation, dynamics and induction.” Physica D: Nonlinear Phenomena 75.1-3 (1994): 11-54. https://www.sciencedirect.com/science/article/abs/pii/0167278994902739
这篇文章介绍了一种理解和量化涌现的方法——层次的ϵ-机器重构算法(Hierarchical ϵ-machine reconstruction)。它能够基于观测数据,对涌现现象进行建模。而要理解这种算法,我们需要从涌现等基本概念说起。
涌现(Emergence)是在复杂科学领域被关注非常多的一个概念,我们之前也介绍过不少关于涌现分类的讨论,例如《涌现的种类与形式》。而这篇文章作者对涌现的理解也有独到之处,值得介绍一下。他把涌现分为三类,和因果科学里的因果阶梯有异曲同工之妙,所以不妨把它称为涌现的三层阶梯。
1.出现新东西(Newness):在这第一层,只要是一个系统的随附特征,都会被囊括进来。比如任何一个多体系统的质心。可以想见,这样定义的涌现是非常广义和平庸的。
2.斑图形成(Pattern formation):进入第二层,我们需要认识到,对于观察者来说随附特征是有区别的。我们会敏感于发现系统展现出来的斑图,这是因为观察者总有偏见,使得我们总对某些编码方式更熟悉。比如相比于一般的云朵,我们会惊讶于某些人脸形状的云,还有在生命游戏里,我们找到并命名“滑翔机”“信号灯”等斑图。当然后者比前者涉及的观察者偏见会更小,更值得被研究,但本质是一样的。涌现的定义到这一层级,就已经是目前很多量化涌现研究的对象了。
3.内在涌现(Intrinsic emergence):最后一层阶梯,系统可以利用自身出现的斑图,影响未来的状态。譬如一个社会系统里的每一个个人,可以学习并使用社会运行的规律,还有蚂蚁会为了整个蚁群牺牲自己。这类似于以前谈论过的向下因果(Downward causation)的概念。
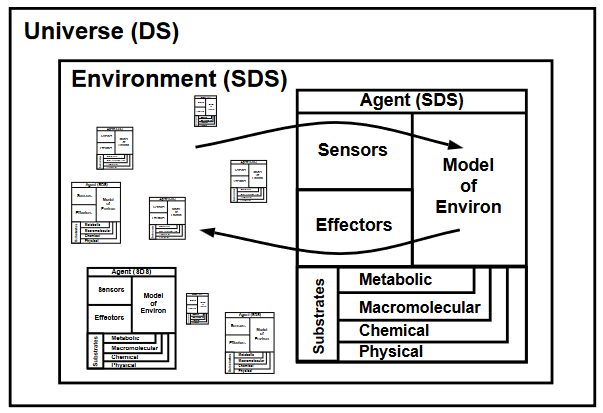
我们熟悉的发生内在涌现的过程有生物进化。它使得我们的世界从无序的原子汤里涌现出各种复杂的生物或组织。生物进化本身是非常复杂的过程,而我们可以用一个世界模型简化地描述它,如下图所示。
整个世界(Universe)可以被看作为确定动力学系统(Deterministic dynamical system,DS)。这里是一个抽象的世界,不涉及拉普拉斯妖和量子力学的讨论。环境定义为其余所有主体构成的系统。在每一个主体的眼中,因为能力有限,环境是一个随机动力学系统(Stochastic dynamical system, SDS)。主体可以通过感受器(Sensors)获取观测数据,同时有效应器(Effectors)做出反应。基于观测数据,每个主体都有对环境建立的模型。感受器、效应器和环境模型都建立在物质构成的基础上,包括物理、化学层面等等。
这个模型可以理解为,给定观测数据(视为一个字符序列),构建一个机器,是对该序列的最佳描述或预测器。所谓最佳,是要在确定性和随机性之间取得一个平衡。理想情况下,应该可以建立一个确定动力系统的模型,从而完美地预测这个世界。但主体资源有限,必须把观测数据的某一部分看作是和规律无关的随机噪音,然后尽可能地把握确定的具有规律的结构,从而有一个对确定和随机部分的合适划分——这实际上也是寻找斑图,识别涌现的过程。
通常我们使用柯式复杂度(Kolmogorov-Chaitin complexity,K(x))来度量一个序列的复杂度。它指的是能够生成序列的通用图灵机(UTM)的最小尺寸。大家认为这是对复杂性一个比较公允的度量,但可惜缺乏通用的算法。其实除了计算问题以外,在某些情况下,柯式复杂度仍然不符合我们的直觉。
假如有一个序列,就是完全随机生成的,那么或许在序列非常短的时候,观察者可以“侥幸”发现规律,用较短的程序去生成它;可当序列变足够长后,是不可能用一个确定的通用图灵机来生成一个完全随机的序列的,除非图灵机就是直接描述序列本身。这时我们发现,柯式复杂度会随着随机性的增加而单调上升。于是乎,一个完全随机的序列会被柯式复杂度度量为非常复杂。可我们知道,随机不等于复杂。比如0和1的随机均匀分布,是很平庸的。所以我们需要一个更合理的复杂度指标。这就有了本篇作者提出来的统计复杂度(Statistical complexity,Cμ(x))。
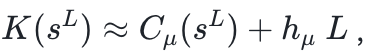
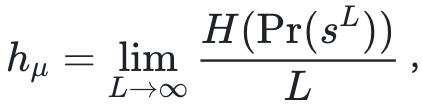
其中Pr(sL)是字符串sL出现的边缘概率分布,H()是求香农熵的操作。或许公式比较抽象,作者给了我们一个简单理解的方式:统计复杂度Cμ(x)是我们允许机器可以hμ以水平犯错的条件下,给出序列最佳预测所需最少的历史信息量。(One interpretation of the statistical complexity is that it is the minimum amount of historical information required to make optimal forecasts of bits in at the error rate hμ.)
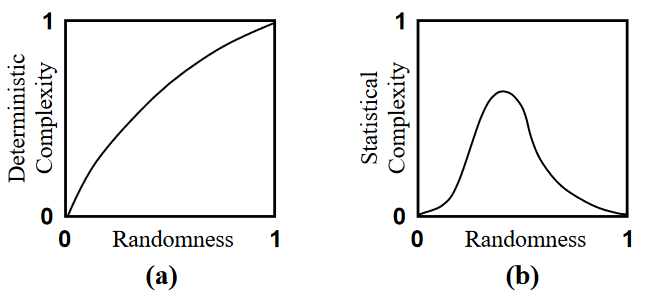
我们可以稍微检验一下这个新指标。当序列是完全确定的时候,香农熵率为0,统计复杂度退化为柯式复杂度,所以对于非常平庸的序列(比如00000…000)复杂度是0。而对于完全随机的序列,柯式复杂度近似于香农熵,也就等于hμL, 所以统计复杂度也是0,符合我们的直觉。两个复杂度指标对比如下图所示。
可以看到,像柯式复杂度这种只考虑确定通用图灵机的确定性复杂度(Deterministic complexity)指标只会随着随机性增加而单调上升,而统计复杂度则在完全确定和完全随机两种情况下度量的值都很低。这符合我们对一般复杂系统的认知,比如计算机上的鸟群模型,会在噪音增加到一定程度时发生相变,过小或过大都不行;还有像伊辛模型,用温度控制无序的程度,在彻底无序和完全有序的中间某一个临界温度上发生相变。神奇的涌现需要系统足够复杂,而这样的复杂性正位于秩序与混沌的边界。
从上面讨论可以看出,统计复杂度仍依赖于预测机器的构造,文章里的一个核心概念 ϵ-机器(ϵ-machine)就是作者给出来的可构造的预测机器。它本身是一个离散的机器,如果面对连续变量的问题,可以以一定分辨率进行粗粒化地观测,得到近似的离散序列。
我们假设主体已经从环境中得到了离散的观测序列,那接下来它要做什么呢?回想我们认识世界的经验,作为主体,接下来就要对观测到的历史数据做归纳,从而对环境做预测。这种归纳,其实就是把观测数据的状态分别对应到我们大脑里的某一个“隐状态”,属于同一个“隐状态”的对未来的预测会有相同的模式。这样的隐状态被作者定义为因果态(casual state)。
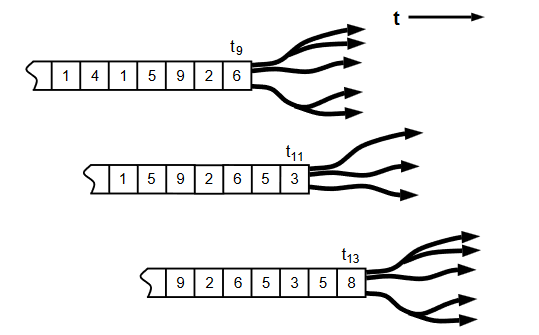
如上图所展示,t9和t13两个时刻对应的序列状态就属于同一个因果态,因为具有相同的未来形态(future morph)。而对应的序列状态就和另外两个处于不同的因果态。为了给出因果态一个形式定义,我们首先给出如下记号:
它们分别表示全序列,未来序列和过去序列。那么属于相同因果态的两个状态t, t’记为:t~t’等价于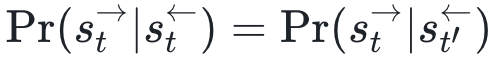 我们进一步给出因果态的集合S,就有了未来形式的定义
我们进一步给出因果态的集合S,就有了未来形式的定义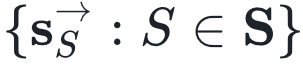 。而导致状态S发生的过去序列的集合就是过去形式(past morph)。
。而导致状态S发生的过去序列的集合就是过去形式(past morph)。
ϵ-机器中的ϵ指的是由观测数据得到因果态的粗粒化映射。有那么多可能的粗粒化映射可以选,为什么我们要关注因果态这一种特殊的宏观态?作者用数学证明告诉我们,因果态是最好的宏观态。首先,对于未来序列的预测,因果态是所有宏观态里最好的,和使用全部观测到的历史信息进行预测效果相当。其次,满足因果态定义的宏观态是唯一的,而且即使能够找到一个和因果态预测效果相当的另一种宏观态,它也不会比因果态有更小的统计复杂度和随机性。可以说,因果态是我们进行编码时的一个理想的信息瓶颈。
知道了因果态是什么,我们便能给出ϵ-机器的形式定义:
其中映射T: S→S指的是转移结构,即St+1=TSt。
基于数据流,估计状态数量以及它们的转移结构和概率的过程被称为机器重构(ϵ-machine reconstruction)。机器重构可以视为一个动态过程,主体在生存时不断调整自己的模型。在这个过程中我们需要关注两个量,熵率和统计复杂度。当主体模型的熵率和环境真实的熵率越接近时,意味着主体预测误差更小,会有更高的生存几率。但这种生存能力是以投入预测的资源为代价的。这个代价就是统计复杂度。
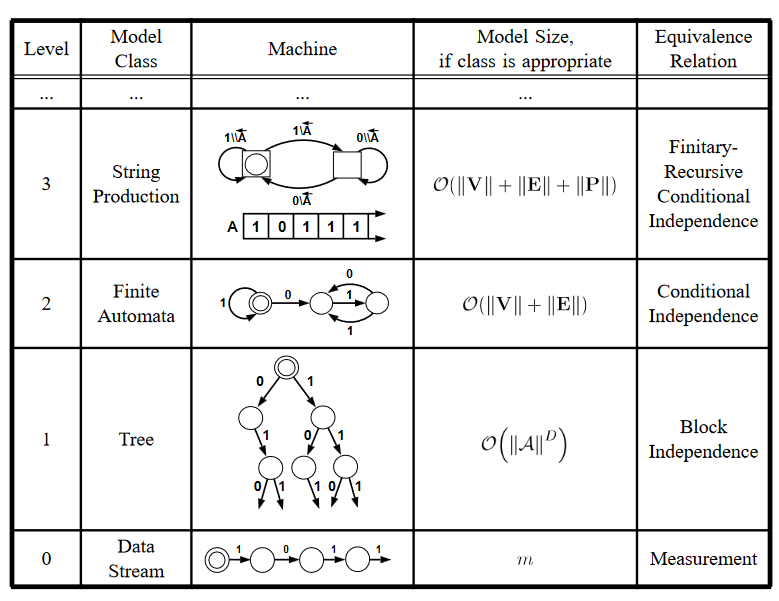
接下来我们进一步讨论机器重构的路径,并从中理解主体是如何实现创新(Innovation)的。这种路径被称作层次的ϵ-机器重构算法。粗略地说,主体首先构建出一个非常简单的模型来预测,然后增加分辨率。当达到当前模型水平的计算能力上限时,便“创新”出一个新的模型类别。这种进化路线没有固定的路径,下表展示了一个可能的过程。
图4. 0级模型:直接描述数据流本身;1级模型:假设序列有周期性,周期长度为D,可以用树结构来进行建模,模型大小是字符集长度的D次方;2级模型:假设序列关联性随时间下降的非常快(近似马尔可夫性),可以用有限自动机(FA)来表示,具有状态V和转移结构E。3级模型:字符生成器(PM), 具有生成规则P。各类模型具体介绍见参考文献。
这里每一次模型升级都有对原本模型节点的打包。下面给出进阶的一般描述。
1.在最低水平上,设定0级模型为描述数据本身,即M0=s
2.从更低模型重构模型Ml=Ml-1/~,其中~表示l级上的因果态等价类。操作的含义是,在l-1级上被区别对待的状态在l级上可以被视为同一个因果态。此时S和T都更新了。
3.收集更多的数据,增大序列长度L, 得到更加精确的一系列模型Ml。
4.如果随着L增大,模型的复杂度发散,即||Ml||→∞,那么回到第二步,得到更高级模型Ml+1。
5.如果模型复杂度收敛,意味着重建好了一个合适的ϵ-机器,程序退出。
我们再尝试用一般的语言去理解这个过程。一个主体为了在一个环境中生存,需要对环境变化做预测,以做出合适的反应。一开始主体只是看到什么就记录什么,几乎没有预测的能力。进化的压力迫使它发现有规律的结构,以便做出预测,哪怕预测是有误差的。随着观测到的数据增多,简单的模型必然需要更大的尺寸才能做好预测。而这个过程如果不收敛,那么总有一个时刻主体没有足够的资源建立如此庞大的机器,就迫使它要跳出之前对机器类别的假设,做出创新,发明更加高明和简洁的机器。如此循环往复,直到某一种机器随着数据量增多不再需要无限制的增加尺寸。
至此介绍完了本篇文章提到的方法框架。James Crutchfield 在信息论方法的道路上深耕了很多年,最近几年似乎在关心信息分解领域的发展。或许在未来,因果涌现、信息分解和计算力学会在某一个交叉点殊途同归。
James Crutchfield 关于计算力学研究的主要文献列表
-
Crutchfield, James P. “The calculi of emergence: computation, dynamics and induction.” Physica D: Nonlinear Phenomena 75.1-3 (1994): 11-54. https://www.sciencedirect.com/science/article/abs/pii/0167278994902739
-
Shalizi, Cosma Rohilla, and James P. Crutchfield. “Computational mechanics: Pattern and prediction, structure and simplicity.” Journal of statistical physics 104 (2001): 817-879. https://link.springer.com/article/10.1023/A:1010388907793
-
Crutchfield, J. P., & Young, K. (1989). Inferring statistical complexity. Physical Review Letters, 63(2), 105–108. https://doi.org/10.1103/PhysRevLett.63.105
-
Hanson, J. E., & Crutchfield, J. P. (1997). Computational mechanics of cellular automata: An example. Physica D: Nonlinear Phenomena, 103(1–4), 169–189. https://doi.org/10.1016/S0167-2789(96)00259-X
希望深入理解计算力学框架的朋友,欢迎参与读书会直播!
涌现无疑是复杂系统诸多现象中最神秘莫测的一个。从鸟群聚集、萤火虫同步、蜜蜂舞蹈,到宇宙起源、生命演化、意识产生,我们生活在一个“涌现”的世界中。所谓的涌现,是指复杂系统在宏观所展现出来的,无法归约到微观的特性或规律。新兴的因果涌现理论有望为量化多尺度复杂系统中的涌现现象提供强大工具。
由北京师范大学教授、集智俱乐部创始人张江等人发起的「因果涌现」系列读书会第三季,将组织对本话题感兴趣的朋友,深入探讨因果涌现的核心理论,详细梳理领域发展脉络,并发掘因果涌现在生物网络和脑网络、涌现探测等方面的应用。读书会自7月11日开始,每周二晚19:00-21:00,预计持续时间10周。欢迎感兴趣的朋友报名参与。

详情请见:
因果涌现读书会第三季启动:深入多尺度复杂系统核心,探索因果涌现理论应用



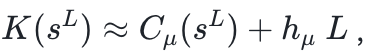
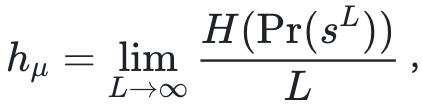
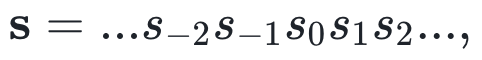
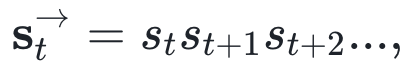
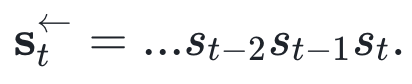
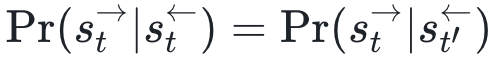 我们进一步给出因果态的集合S,就有了未来形式的定义
我们进一步给出因果态的集合S,就有了未来形式的定义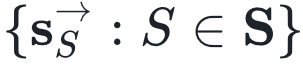 。而导致状态S发生的过去序列的集合就是过去形式(past morph)。
。而导致状态S发生的过去序列的集合就是过去形式(past morph)。