如何让机器识别涌现？基于数据驱动的多尺度因果涌现框架｜周日直播·因果涌现读书会第三季

导语

如何让机器超越具体的像素，识别出照片中的猫和狗？这个过程本质上是一个涌现识别的任务，我们人类时时刻刻都在进行，从山峰和云朵中看出各种奇特的形状，从字词中理解文章的含义。从因果涌现理论的视角而言，涌现的发生取决于观察的尺度，我们要如何让机器学习到合适的尺度，并识别出涌现呢？在本周日因果涌现读书会第三季的分享中，北京师范大学系统科学学院硕士生杨明哲将介绍团队的最新工作，该研究在之前神经信息压缩器（Neural information squeezer，NIS）的基础上提出NIS+框架，解决了最大化有效信息（EI）这一重要问题，并可以拓展到许多经典的复杂系统上，具有更好的泛化预测能力。

1. 涌现的定义和量化

天空中的鸟群，地上的蚂蚁，都演绎出瑰丽的神奇景象——涌现。涌现现象是复杂系统的重要特征，也和我们的生活息息相关，比如人脑意识是大脑众多神经元的涌现，而人工神经网络也能在参数规模较大的时候，具有一些“涌现能力”，例如最近很火的大语言模型，其中可能就发生了重要的涌现现象。

图1. 大模型根据提示生成的关于人脑意识的图片

这种突然冒出来的“多者异也”，固然很神奇，那从研究者的角度来看，为什么它会具有研究的价值？其实涌现的发生取决于观察的尺度，是观察者认识和参与世界的重要途径。比如你在读一本书的时候，最基本的阅读单元也就是汉字，而不会把它们看成一堆笔画的组合。世界中到处都有信息和噪声，而我们需要节约注意力，用尽可能少的成本对世界的未来做出更泛化的预测。很多机器和人工智能，学不会在发生涌现的尺度上观察世界，于是只能在特定的测试集上表现良好，比如去识别草地上的狗，而一旦到了陌生的数据环境，就会失去泛化预测能力，因为它在训练的时候更多见到的就是草地上的狗，于是把构成草地的像素和构成狗的像素混为一谈，而没能把狗当成一个整体来看。

那要怎么解决这一问题呢？这本质上其实就是一个涌现识别的任务，而在识别任务之前，我们需要先做好对涌现现象的定义和量化。本次读书会，我们会先介绍目前已有的量化涌现的框架，包括计算力学、G-emergence、信息分解和 Erik Hoel 的多尺度因果涌现框架，对它们的优劣之处进行比较。

2. 多尺度因果涌现框架

进一步，读书会中将着重展开多尺度因果涌现框架。其核心思想很简单。我们首先建立起对一个系统的多尺度观察视角，可以分为微观尺度和不同的宏观尺度。从微观变量到宏观变量的降维过程，便是粗粒化（coarse-graining）。在不同尺度上，都有其各自尺度上的动力学。我们可以度量每个动力学的因果效应的强度，当有宏观动力学的因果效应强度大于微观动力学时，我们认为发生因果涌现。

图2. 因果涌现框架。左图横轴是时间，纵轴是尺度，通过比较不同尺度上的动力学因果效应强度来判定是否发生因果涌现。右图展示一个离散的马尔科夫动力学上的因果涌现案例。

因果效应强度可以用有效信息（effective information，EI）来度量，关于这个概念的具体介绍可以参考《量化因果涌现表明：宏观可以战胜微观》。为什么谈涌现就要谈因果这个概念？所谓涌现，其实就是在某个尺度上，你发现从动力学的输入（过去的某一时刻），去预测动力学的输出（展望未来），是一个比较确定的过程，同时从未来再回溯过去，也是一个比较确定的过程。这就是一个简洁有力的观察尺度。而这种思想就和近年来因果科学的发展产生密切的关联。Judea Pearl 对因果这个概念的定量化描述，就为涌现的量化工作提供了适当的工具。

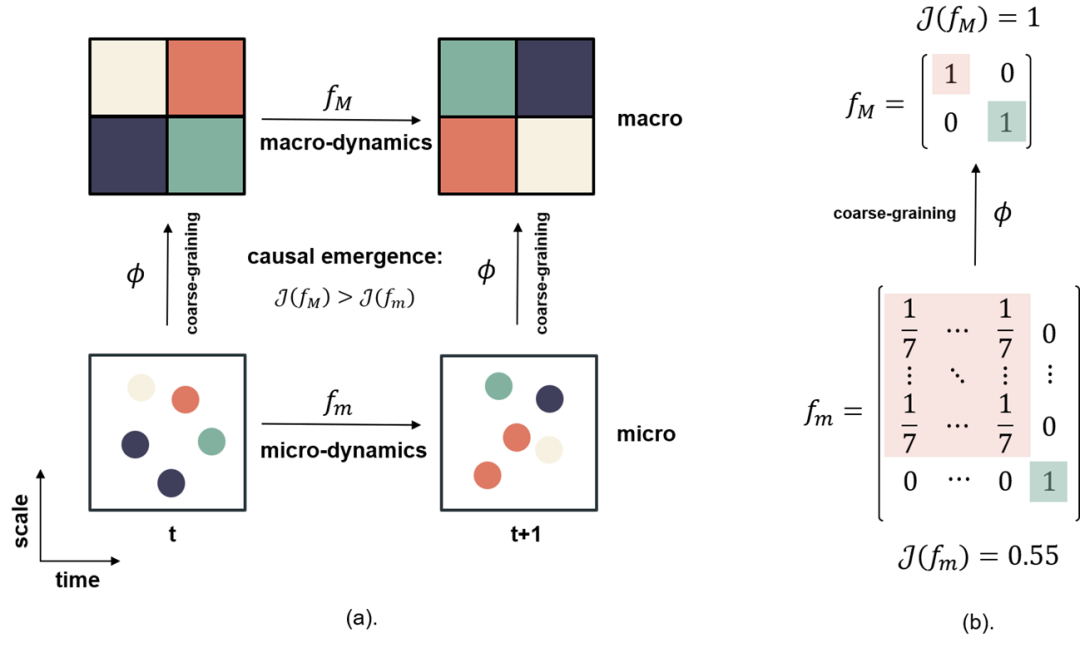
Hoel, E. P., Albantakis, L., & Tononi, G. (2013). Quantifying causal emergence shows that macro can beat micro. Proceedings of the National Academy of Sciences, 110(49), 19790–19795.

如上图所示，多尺度因果涌现框架一开始定义在马尔科夫动力学系统上。给定一个马尔科夫转移矩阵，我们可以计算其有效信息大小，然后比较不同尺度上动力学的有效信息。不难发现，接近于一一对应的可逆映射的马尔科夫转移矩阵，会有更高的EI值，这一点和我们的直觉是相符的。不过我们面临的很多问题可不是简单的离散马尔科夫系统，而很有可能就是连续的动力学。另外，这个粗粒化策略到底是怎样制定的？它真的发掘出最有价值的观察尺度了吗？这实际上需要我们一方面把该框架延拓到更多类型的动力学上，另一方面我们需要解决一个优化问题，即如何找到一个最合适的粗粒化策略和相应的宏观动力学。而且大多数情况下，没人告诉我们一个系统的动力学方程该怎么写，而是一个数据驱动的任务。于是和机器学习领域的结合就是非常必要的了。

3. 识别因果涌现：从NIS到NIS+

目前已经有工作在尝试解决这一问题，典型就是神经信息压缩器（Neural information squeezer，NIS），读者可以参考《什么是涌现？人工智能给你答案》来了解这一方法。不过NIS没有真正解决最大化EI的问题，而且只是在一些轻量级的模型上验证了这一想法。

NIS 工作：Zhang, J., & Liu, K. (2022). Neural Information Squeezer for Causal Emergence. Entropy, 25(1), 26.

本期读书会主要介绍的是另一个新工作，NIS+，从名字上很容易看出它是对NIS的继承和修正。不过它并不是调几个参数这么简单，而是真正解决了最大化EI的重要问题，同时将框架拓展到更多的经典复杂系统上，甚至也应用在了真实的核磁共振脑数据上，得到一些有意思的验证结果。相应地，我们也在数学上证明了该框架能够最大化EI。

NIS+ 工作

论文题目：Finding emergence in data by maximizing effective information

作者：杨明哲，王志鹏，刘凯威，荣英淇，袁冰，张江

论文地址：https://arxiv.org/abs/2308.09952

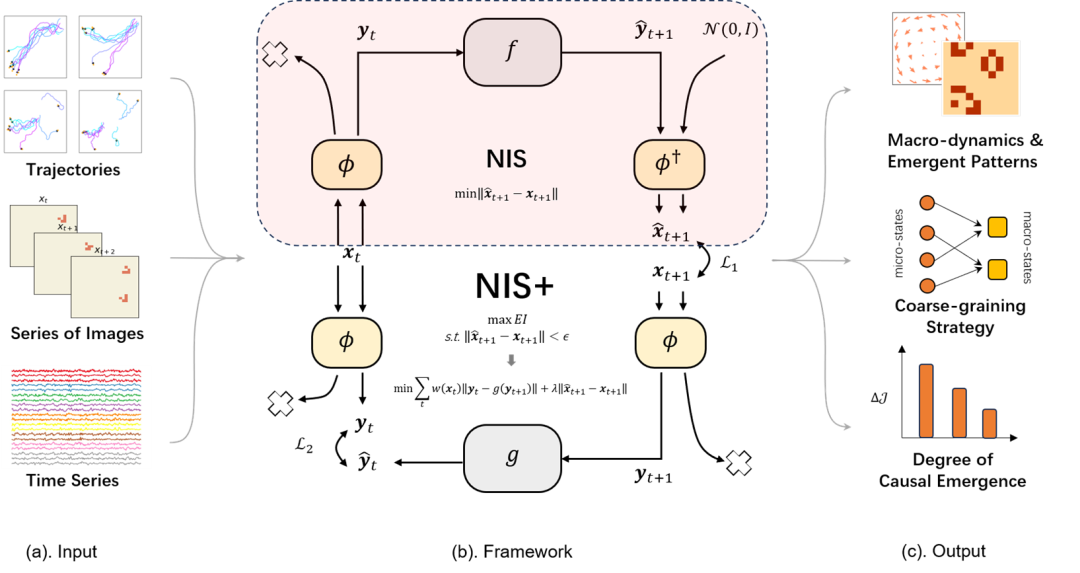
图3. NIS+框架的概览，输入各种多元时间序列，可以输出不同尺度EI的比较结果，最佳粗粒化策略和涌现的宏观动力学等。

数学细节这里不多展开，我们就从直觉上来理解为什么改造后的NIS+可以最大化EI。回到前面所讲述的确定性和简并性，通常机器学习动力学都在从t时刻去预测t+1时刻，这实际上是在注重确定性，而NIS+还要训练一个反向动力学，从t+1时刻回溯去预测t时刻的变量状态。如果这种反向动力学可以预测的很好，说明编码器得到的宏观变量适合低简并性的动力学演化，从而进一步影响动力学的学习。如果得到的宏观动力学确定性高，简并性低，便是一个EI很高的动力学。NIS+还有一个样本重加权的操作，和EI要求输入被干预为均匀分布相关。

最大化EI确实可以帮助我们解决实际问题吗？正如在文章开头我们所提到的，识别涌现理应帮助我们具有更好地泛化预测能力。在这篇文章的实验上，我们在toy model上，以及在鸟群和生命游戏这类经典的计算机模拟的复杂系统上都验证了NIS+具有更好的泛化预测能力。

4. 实验结果

首先介绍一下NIS+在含观测噪音的SIR感染动力学模型上的成果。该实验目的是验证框架的有效性，所以使用了已知的动力学模型SIR病毒感染动力学，选取了S和I两个变量的动力学方程，通过加噪音的方式扩维成4维的微观变量。以微观变量作为观测数据，我们在二维的宏观尺度上观测动力学学习情况，发现NIS+学习到的宏观动力学确实在EI上有显著的提高。这里我们不仅跟之前的NIS框架对比，还和普通的神经网络（NN）以及变分自编码器（VAE）做对比，还包括了结合样本重加权和反向动力学学习技术的各种框架。在多步预测结果上，我们可以主要关注部分样本集（图中红色柱子）上训练的结果。结果表明NIS+有更低的预测误差，而这真正体现出了NIS+具有更强的分布外泛化预测能力。

图4. 含噪音的SIR动力学模型的部分实验结果图

然后看鸟群模拟上的实验。我们设定的鸟群实验是共有两群鸟，每群各8只鸟。而每只鸟分别有表示速度和位置的4维向量，所以微观上是64维向量。经过搜索优化，我们在8维的宏观尺度上找到EI最大的宏观动力学，恰好可以对应两个鸟群的位置和速度。而在泛化测试上，我们选择调整初始数据的鸟群半径。当半径变大时，鸟群在接下来的运动中更容易发散，也就更难预测。我们发现NIS+在这项测试上也能达到更好的泛化效果。

图5. 鸟群模型的部分实验结果图

生命游戏则是跟鸟群不一样的经典复杂系统。它作为一种特殊的元胞自动机，涌现现象就像是绳子的上下震动形成了一个行进的波。生命游戏上的各种图案，包括滑翔机、信号灯等等，就是这样的一个个“准粒子”。我们用了一个略微不同的框架来识别这个模型上的涌现现象。因为规则影响的传播需要时间，于是我们进行时空粗粒化，即微观上两个时间步对应宏观上的一个时间步，而在空间上我们先划分好一个个九宫格区域，在每个九宫格上使用一个编码器。这些编码器并联在一起，就构成整个的粗粒化函数。这其实也是这篇文章里提出来的一种拓展方式，事实上我们可以把编码器进行串联并联等各种组合，来应对不同类型的复杂系统。在各种图案的泛化测试上，NIS+也确实表现出更高的准确率。

图6. 生命游戏模型的部分实验结果图。

那在真实的核磁共振脑数据上，我们又能发现什么有意思的结果呢？我们选取的数据，来自正在看电影的人的核磁共振脑数据。在进行搜索优化后，我们发现在一维的宏观尺度上EI最高，在用积分梯度法进行归因后，我们发现和那一维的宏观变量最相关的微观变量都落在了视觉区脑区上。或许观看这一行为的发生就是视觉区神经元的协同作用。等到以后NIS+的框架可以拓展到拟合能力更强的神经网络框架上时，我们可以期待它能在脑数据上发掘出更有意思的结果。

图7. 核磁共振脑数据的部分实验结果图

5. 总结

总的来说，NIS+输入的，是各种各样多元的时间序列数据，而它可以通过训练告诉我们，这其中是否有因果涌现发生，如果有，那么最合适的宏观尺度是哪一个，最佳粗粒化策略是什么，以及那个涌现出来的宏观动力学究竟长什么样子。我们相信这个框架还有可改进之处，而NIS+的初步成果至少告诉我们，涌现现象是我们了解和预测一个复杂系统时，可以充分利用的一个途径。

主讲人简介

杨明哲，北京师范大学系统科学学院硕士生，在张江老师因果涌现研究小组。研究领域是因果涌现、复杂系统自动建模。

学者主页：https://pattern.swarma.org/user/76769

内容大纲

引言
涌现识别问题背景
NIS+方法框架
NIS+实验结果
总结和展望

核心概念

因果涌现
有效信息
粗粒化
神经信息压缩器（Neural information squeezer，NIS）
样本重加权
分布外泛化

直播信息

时间：12月10日（本周日）上午9:00-11:00

参与方式：

斑图地址：

https://pattern.swarma.org/study_group_issue/569

扫码参与因果涌现读书会，加入群聊，获取系列读书会回看权限，加入因果涌现社区，与社区的一线科研工作者沟通交流，共同推动因果涌现这一前沿领域的发展。

参考文献

Yang, M., Wang, Z., Liu, K., Rong, Y., Yuan, B., & Zhang, J. (2023). Finding emergence in data by maximizing effective information (arXiv:2308.09952).

Crutchfield, J. P. (1994). The calculi of emergence: Computation, dynamics and induction. Physica D: Nonlinear Phenomena, 75(1–3), 11–54.

Barnett, L., & Seth, A. K. (2023). Dynamical independence: Discovering emergent macroscopic processes in complex dynamical systems. Physical Review E, 108(1), 014304.

Rosas, F. E., Mediano, P. A. M., Jensen, H. J., Seth, A. K., Barrett, A. B., Carhart-Harris, R. L., & Bor, D. (2020). Reconciling emergences: An information-theoretic approach to identify causal emergence in multivariate data. PLOS Computational Biology, 16(12), e1008289.

Hoel, E. P., Albantakis, L., & Tononi, G. (2013). Quantifying causal emergence shows that macro can beat micro. Proceedings of the National Academy of Sciences, 110(49), 19790–19795.

Yurchenko, S. B. (2023). Can there be a synergistic core emerging in the brain hierarchy to control neural activity by downward causation? [Preprint]. Preprints.

Zhang, J., & Liu, K. (2022). Neural Information Squeezer for Causal Emergence. Entropy, 25(1), 26.

Dinh, L., Sohl-Dickstein, J., & Bengio, S. (2016). Density estimation using Real NVP. International Conference on Learning Representations,International Conference on Learning Representations.

Kemeth, F. P., Bertalan, T., Thiem, T., Dietrich, F., Moon, S. J., Laing, C. R., & Kevrekidis, I. G. (2022). Learning emergent partial differential equations in a learned emergent space. Nature Communications, 13(1), 3318.

（参考文献可上下滑动查看）

因果涌现社区

跨尺度、跨层次的涌现是复杂系统研究的关键问题，生命起源和意识起源这两座仰之弥高的大山是其代表。因果涌现理论、机器学习重整化技术、信息论或信息分解等近年来新兴的理论与工具，有望破解复杂系统的涌现规律。

集智俱乐部因果涌现读书会目前已经进行了三季。第一季读书会系统地梳理了因果涌现的概念，以及它与Sloopy Model、复杂性阈值、自指等概念之间的联系，也探讨了因果涌现理论在复杂网络、机器学习中的应用。参看：因果涌现读书会启动：连接因果、涌现与自指——跨尺度动力学与因果规律的探索。

第二季读书会探讨了涌现、因果科学和机器学习三大主题的融合，包括信息论拓展、因果涌现理论、因果表示学习、多尺度机器学习动力学建模。请参看：因果、涌现与机器学习：因果涌现读书会第二季启动。

第三季读书会进一步围绕因果涌现的核心问题「因果涌现的定义」以及「因果涌现的辨识」进行深入学习和讨论，对 Erik Hoel 提出的 Causal Emergence，Causal Geometry 等因果涌现的核心理论进行探讨和剖析，并详细梳理其中涉及到的方法论，包括从动力学约简、隐空间动力学学习等其他领域中学习和借鉴相关的研究思路，最后探讨因果涌现的应用，包括基于生物网络、脑网络或者涌现探测等问题展开扩展，发掘更多的实际应用场景。请参看：因果涌现读书会第三季启动：深入多尺度复杂系统核心，探索因果涌现理论应用

此次读书会主题是「新信息论：从分解到整合」，是因果涌现系列读书会的第四季，将重点梳理信息分解与整合信息论的相关研究。请参看：新信息论：从分解到整合｜因果涌现读书会第四季启动

因果涌现社区聚集了600+成员，积累了大量论文解读资料。欢迎感兴趣的朋友报名，加入因果涌现社区，解锁对应录播权限。

因果涌现读书会回放视频

第一季：https://pattern.swarma.org/study_group/7

第二季：https://pattern.swarma.org/study_group/16

第三季：https://pattern.swarma.org/study_group/28

第四季：https://pattern.swarma.org/study_group/35

因果涌现社区共创的文章