2023年伊始,ChatGPT引爆了社会各界对人工智能发展前沿的关注,尤其是ChatGPT背后的核心技术——大语言模型。大语言模型为什么会涌现出强大的学习能力?从复杂科学视角,AI 大模型可以看作与生态网络类似的复杂适应系统,展现出复杂系统常见的现象规律,例如涌现、规模法则等。因此,复杂系统的研究方法可以为理解和改进 AI 大模型提供深刻的洞察,并有助于构造可解释性的AI模型。
为深入探讨人工智能与复杂科学前沿进展,集智俱乐部自2023年初组织了一系列AI相关主题的读书会,从「后ChatGPT」到「AI+Science」系列,从「图神经网络与组合优化」到「通用人工智能(AGI)」,从「大模型安全与对齐」到「大语言模型与多智能体系统」,从不同视角思考AI对人类社会将产生的广泛影响,欢迎感兴趣的朋友参与(详情请见“读书会列表”)。2024,我们一起探索复杂世界的简单规则!
关键词:AI 大模型,复杂适应系统,涌现,规模法则,渗流模型,范畴论
1. 作为复杂系统的AI大模型
-
神经网络与复杂网络
-
作为复杂动力系统的前馈运算与训练
-
自注意力是一种自调控机制
-
大语言模型中的涌现
-
大语言模型的规模法则
2. 作为复杂适应系统的AI大模型
二、用AI大模型辅助复杂系统研究
1.复杂系统自动建模
2.大语言模型中的知识提取
3.通用领域的AI大模型
最近,人工智能再一次被人们推上了风口浪尖。究其原因就在于以ChatGPT为代表的AI大模型展示出了令人惊艳的表现,仿佛通用人工智能在一夜之间就已经来到了我们的身边。本质上讲,ChatGPT无论在架构还是在方法上都与以前的模型没有本质区别,然而仅仅就是把数据量和模型参数量提升上去,这些大模型就一下子拥有了很神奇的能力。比如,ChatGPT能通过和用户对话而自动学习知识,还能够在一定的引导下完成较为复杂的推理能力。关键是,所有这些新能力,都并不是该模型训练学习的目标,它是随着参数量规模的增大,而自发产生的——研究者把这样的现象,称之为“涌现”(Emergence)。
对于复杂系统科学(以下简称复杂科学)研究者们来说,涌现是一个再熟悉不过的概念了。一个复杂的人工智能大模型能够展现出涌现的能力,这本身就暗示着,现在的大模型已经成为了一个不折不扣的复杂系统。不仅如此,大模型超级强大的学习能力,使得这个复杂系统还能够灵活地适应环境,甚至能够展现出在少量提示下就可以学到全新技能的所谓 in-context 的学习能力。从结构上说,大模型之所以能够表现如此惊人,就在于其深度的层级结构,这种结构是一种自发演化形成的复杂网络。从动力学角度上说,大模型的运作分成了两个相互作用的耦合动力学:一个是更加快速的前馈动力学,另一个是较为慢速的学习反馈动力学。而从宏观的定量表现角度说,大语言模型也会具有像生物体、城市、公司这样的复杂系统都具备的“规模法则”(Scaling law),以及临界相变等表现。这一切都说明,似乎复杂科学中的那些分析工具都能应用到AI大模型。
那么,这些大模型会不会成为复杂科学下一个热点研究对象呢?我们可以从复杂系统科学及其发展的角度探讨这个问题。
1972年,著名的凝聚态物理学家,诺贝尔奖得主Philip Anderson就在Science上发表了一篇影响深远的文章:《More is Different》。文章指出,我们不能指望将微观原子世界的规律了解清楚之后,就能自然而然地了解诸如细胞、大脑、城市等等这些宏观复杂系统的规律,这二者是非常不同的。
之所以简单粗暴地将细胞还原成一堆原子的集合,将大脑还原成一堆细胞的集合这种做法是行不通的,关键就在于所有的复杂系统之中都存在着涌现的特征。该文指出,“Emergence is when quantitative changes in a system result in qualitative changes in behavior”,即“系统定量上的变化可以导致系统行为上的定性变化,这就是涌现”。用亚里士多德的话来解释,就是“整体大于部分之和”,即整体上展现出了构成它的个体所不具备的新特性。
涌现之所以发生是和关系而非要素有着密切联系的。一堆电子元件的简单堆砌不能构成一台电脑,这是因为电子元件之间以及元件和环境之间存在着关联和相互作用。通过这些复杂的相互作用,系统往往表现出非线性、涌现、自组织等性质。
在其中,复杂系统的适应性能力又是一个我们应特别关注的现象,它表现为能够灵活地随环境的变化而改变。例如,一场森林大火并不能破坏整个生态系统,相反,有些时候它还会对清理杂草有很大的好处。这种灾后重生的能力就是生态复杂系统的适应性能力。著名的已故复杂科学家、遗传算法的发明人,John Holland 将这种具备适应能力的复杂系统称为复杂适应系统(Complex Adaptive Systems,简称CAS)。
那么,面对这样丰富多彩、精彩纷呈的复杂适应系统,人们又该如何对其进行研究呢?答案是——建模。即通过数学或计算机在符号世界中再造一个复杂系统,这就是复杂科学研究的内容。可以说,复杂科学数十年的发展历史就是复杂系统建模,及其对模型进行研究的历史。正是因为此,复杂科学的发展具有明显的方法、技术驱动的特点。
90年代的时候,随着计算机的普及,人们开始构建各式逼真的计算机模拟模型,于是“多智能体模拟”技术催生出了复杂科学这一门全新学科。从“生命游戏”到“遗传算法”,再到“人工股市”,这些多主体模型无一不活灵活现,将现实世界的复杂性再现到了计算机世界之中(参考《虚实世界》)。
然而,到了2000年,随着大数据的积累,“数据驱动”的复杂性研究成为了复杂科学的主流。人们已经不满足于单纯地构建计算机模型,而是热衷于针对大数据展开分析,从而试图发现真实世界复杂系统的普适性规律。例如,“规模法则”(Scaling Law)就是人们在真实数据中发现的一条黄金法则,无论是生物体还是城市,抑或是网络社区,这些复杂系统的宏观变量都会随着系统的规模而呈现幂律增长。著名的克莱伯定律(Kleiber Law)就是生物界的一个规模法则,它指出生物体规模每增长百分之一,则它的新陈代谢率仅仅增长0.75%。该定律还能推导出诸如“哺乳动物一生的心跳次数是一个常数”这样的惊人结论(参考《规模》,以及我的课程《复杂科学的前世今生》)。

地址:https://campus.swarma.org/course/41?from=wechat
2010年代后,随着人工智能时代的来临,大数据终于催生出了AI大模型这一全新的物种!从建模能力来说,无人能与现在的基于神经网络和深度学习的AI大模型相媲美。那么,复杂系统研究又会不会因AI大模型的出现而有所改变呢?笔者认为,这有两种全新的研究方向:
>> 在集智俱乐部「后ChatGPT读书会」第二期,北京师范大学系统科学学院教授、集智俱乐部创始人张江教授详细探讨了“复杂适应系统视角下的 ChatGPT 与 AI 大模型”,欢迎感兴趣的朋友加入读书会并观看回放视频。

AI大模型首先是一个典型的复杂系统。我们以目前异常火爆的ChatGPT为例来说明。首先,ChatGPT其实就是一个超级庞大的神经网络。这里面,一个个神经元就构成了ChatGPT这个复杂系统的基本组成单元,而这些神经元彼此之间复杂的相互连接就构成了一个复杂网络。
神经网络与复杂网络
与绝大多数复杂网络不同,人工神经网络是一个处于不断变动之中的加权有向网络。随着训练的进行,大量的连边实际上都会被“砍掉”的,最后无论哪个层次,都会形成“胜者通吃”的局面,即各个神经元上的权重分布会呈现异质化趋势。
论文题目:Characterizing Learning Dynamics of Deep Neural Networks via Complex Networks
论文地址:https://arxiv.org/pdf/2110.02628.pdf
不仅如此,随着训练的进行,神经网络会自发演化出不同的局部网络结构(Motif):
论文题目:Emergence of Network Motifs in Deep Neural Networks
论文地址:https://www.mdpi.com/1099-4300/22/2/204
在这篇文章中,作者还展示了网络指标也能够反映出训练集、激活函数等不同要素的特征。然而,目前的研究还局限在较小规模的网络中,更大规模的结构又会如何影响网络的功能和学习能力呢?目前尚不得知。
论文题目:Deep Neural Networks as Complex Networks
论文地址:https://arxiv.org/abs/2209.05488
作为复杂动力系统的前馈运算与训练
从动力学角度上来说,神经网络本身就是一个复杂的动力系统。如果我们将每个神经元的激活状态看作是每个节点的状态,那么整个神经网络在执行前馈运算的过程中,就体现为一个高维空间中的动力学演化过程。例如,前馈神经网络在给定输入后可以通过动力系统的吸引子来赋予网络记忆的能力。
论文题目:A Recurrent Neural Network that Learns to Count, Connection Science
论文地址:https://www.tandfonline.com/doi/abs/10.1080/095400999116340
这篇文章将基于ResNet网络结构的神经网络理解为一个动力系统,从而讨论其动力学的稳定性问题。
论文题目:Stable Architectures for Deep Neural Networks
论文地址:https://arxiv.org/pdf/1705.03341.pdf
除了前向动力学过程以外,神经网络的训练过程则可以体现为一个神经网络权重空间中的动力学。由于很多机器学习任务都可以看作是一个优化问题的求解,而最常用的训练算法就是所谓的随机梯度下降方法,这样,整个网络的训练过程便可以看作是一个势场中的扩散过程,不同的随机梯度下降算法(例如动量梯度下降等)又可以看作是不同类型的扩散过程,如包含漂移项等。于是,神经网络的学习过程就可以被一个朗之万(Langevin)方程来建模,这样非平衡统计物理中的大量分析工具便可以被应用到神经网络训练过程中来 。
论文题目:Rethinking the Structure of Stochastic Gradients: Empirical and Statistical Evidence
论文地址:https://openreview.net/forum?id=9xlU4lhri9&referrer=%5Bthe%20profile%20of%20Zeke%20Xie%5D(%2Fprofile%3Fid%3D~Zeke_Xie1
论文题目:Anomalous diffusion dynamics of learning in deep neural networks
论文地址:https://www.sciencedirect.com/science/article/abs/pii/S0893608022000296
不仅如此,这篇文章还指出,通过控制轨道的Hausdorff维度可以调控神经网络的训练过程,越重尾的分布可以让模型具有越好的泛化能力。
论文题目:Non-convex learning via Stochastic Gradient Langevin Dynamics: a nonasymptotic analysis
论文地址:https://arxiv.org/abs/1702.03849
论文题目:Hausdorff Dimension, Heavy Tails, and Generalization in Neural Networks
论文地址:https://arxiv.org/pdf/2006.09313.pdf
如果将两种动力学结合起来看,则神经网络大模型是一个典型的两个不同时间尺度上的动力学过程,一个是小时间尺度上的前馈过程,另一个则是更大时间尺度上的反馈训练过程。这样两种时间尺度的协调与配合便会使得神经网络展现出极强的适应性能力。后文将对这种两个尺度的动力学进行更深入地讨论。
自注意力是一种自调控机制
另外,值得一提的是,目前所有的大语言模型都采用了Transformer架构,而这一架构的其中一个核心部件就是自注意力机制。有了注意力机制的引入,实际上神经网络在前向动力学中就可以动态地决定一个加权有向网络,该网络可以反作用到神经网络上,从而相当于在前向动力学过程之中就形成了一种高阶的控制结构。
论文题目:Attention Is All You Need
论文地址:https://arxiv.org/abs/1706.03762
如上图所示,所谓的自注意力机制其实就是一个自动根据节点特征向量构建加权有向图的过程。这里面的每一个节点表示输入给自注意力层的一个神经元,每个神经元都有三组节点特征向量,分别定义为Query、Key和Value。那么,对于任何两个神经元i和j,它们之间有没有链接呢?这就要由i的Query向量与j的Key向量的内积来决定了。我们不妨把Query理解为一把钥匙,而Key则理解为一把锁,二者的内积大小就是钥匙和锁的匹配程度,这个程度的值就是i应该关注j的注意力大小,它是一个从i指向j的权重值。
进一步,为什么要构建这个网络呢?答案就是,为了提取信息。有了这个注意力数值,i就可以从j的身上来提取信息了(也就是储存在V向量中的信息)。然而,与一般的网络动力学不同的是,这个注意力网络本质上是由神经网络的前馈过程来决定的,也就是说随着输入给注意力机制的信息不同,最终得到的注意力网络也是不同的。于是,各个神经元之间便可以在前馈运算过程中随着流入信息的不同而形成不同的信息通路。
我们不妨把一个前馈运算过程和网络权重比喻成水流和河道。一般的神经网络河道是慢变的,水流只能被动地在河道中流淌,而只能通过缓慢的训练过程慢慢改变河道。但是,有了自注意力这种机制,河水能够在流淌的过程中就改变河道的分布情况,这就使得单一的前馈运算过程就已经成为快慢两种时间尺度混合的动力学过程了。

图3. 在最近1000年中,不断改变中的 Willamette河流
其实,在一般的多变量的复杂动力系统中,这种现象本质上可以理解为快、慢变量的分离。例如,一个复杂动力系统可以写为:dX/dt=f(X),其中变量X包含了两部分:X1和X2。其中,X1的变化时间尺度非常快,而X2的变化时间尺度非常慢,这就实现了快-慢变量的分离。协同学的提出者哈肯(Haken)曾专门讨论过一般随机动力系统中的变量分离方法(参考《协同学原理》)。有了快、慢变量的分离,我们便可以将 f 理解为两个分离的动力系统,一个是 f1,它对应的是 X1 变量的快动力学,这个时候 X2 便构成了 f1 快动力学的参数,而另外的慢动力学 f2 则制约了参数 X2 的动态演化,对 X2 的改变就有可能彻底改变了 f1 动力学的运行方式,因此我们也可以说 X2 调控了 f1 这一快动力学。
在神经网络中,快动力学是前馈过程,网络权重W是参数,慢动力学是梯度反传算法,对W进行调整。Transformer中的自注意力机制的本质就在于前馈过程可改变注意力,而注意力又可以看作是一种动态权重加到每个神经元的数值上,它的作用是和W类似的。这就导致了一种自我调控的实现(即表现为f1可以改变f2)。即系统的“快”动力学能够在一些情况下决定“慢”动力学。
从图灵机的角度来说,前馈的消息可以看作是数据,网络权重W可以看作是调控程序。学习的过程就体现为程序的改变。因而配备了自注意力机制的神经网络本质上是可以做到自我调控的。这种调控手段很类似于基因网络的自我调控机制。一个基因在整个过程中既可能成为调控者,又可能成为被调控的对象。或者说,调控者可以被看作是程序,被调控对象可以被看作是数据。所以,自注意力机制使得神经网络具备了“自我编程”的能力(参看递归函数论中的s-m-n定理),即调整W就是在改变程序。我们猜测,这是ChatGPT这样的大语言模型能够实现 in-context 学习,以及各种复杂推理功能的核心。
例如,最近微软研究院的一篇文章就指出,大语言模型能够在自注意力机制中模拟梯度下降算法,从而实现in-context学习。这篇文章背后的基本原理就在于注意力本身的调节可以被看作是一种对权重W的梯度下降过程,因此注意力的调节其实就等价于机器在实现程序的自我修改。
论文题目:Why Can GPT Learn In-Context? Language Models Secretly Perform Gradient Descent as Meta-Optimizers
论文地址:https://arxiv.org/abs/2212.10559
大语言模型中的涌现
大语言模型的涌现现象也是近年来研究的热点问题,但是与传统复杂系统中的涌现定义不同,大语言模型的涌现能力,指的是随着模型规模的增长,一些能力会突然变强,突变式地拥有了小语言模型所不具有的新能力。
论文题目:Emergent Abilities of Large Language Models
论文地址:https://arxiv.org/abs/2206.07682
https://pattern.swarma.org/study_group_issue/504
上图展示了不同大语言模型在不同类型的任务上的表现随模型的规模(这里是训练的时间周期)而变化的趋势。这八张图都展示出了突变模式,即当规模增长到一定程度后,某些能力就会突然表现得很好。具体的涌现能力往往使用模型的 prompting(in-context learning)能力来刻画,这是大型语言模型最核心的能力。Prompting 是指不需要任何训练或者梯度更新,只需改变输入,在输入中添加一些提示文本(如对任务的描述、规则的定义等),使模型在此基础上补充回答。需要注意的是涌现出来的 few-shot prompting 能力是不可预测的,因为这些能力并没有包含在预训练任务中,并且我们只会进行few-shot prompting。因此,我们无法知道语言模型执行 few-shot prompting 任务的全部范围。所以如何更好地解释 prompting 有效的机理显得尤为重要,对在更小模型上产生涌现能力有现实的帮助。
需要注意的是虽然解锁涌现能力的方法有很多,包括:1)进一步扩大模型规模;2)提高数据的质量以及改善模型架构和训练方式;3)改善语言模型的通用 few-shot prompting 能力。但是并非大语言模型中所有的任务都会发生涌现。同时随着语言模型增大会产生涌现能力,但是,风险也在增加。因此弄清楚发生涌现的真正机理到底是什么显得尤为重要。这有助于我们确定模型可以拥有哪些涌现能力,以及如何训练一个具有更强的语义模型。对于某个任务只有模型规模超过某个阈值才能发生涌现能力,如果把大语言模型看成是一个具有世界知识的复杂系统,可以进行如下解释,如果一个多步推理需要L步的序列计算,这可能需要模型至少有O(L)层深度的网络,因此,更多的参数和更多的训练模型能够确保更好地记忆那些有助于各类任务的世界知识。再比如说,要在 closed book 问答上取得好的表现,可能需要一个模型具有足够的参数来捕获知识库本身。除了发生真正的机理会导致大模型发生涌现能力,评估涌现能力指标的选择以及交叉熵损失函数的使用,都会影响模型涌现能力的发生。因此,我们更需要借助复杂系统的研究理论来解释发生涌现现象的本质。
从复杂科学的视角来看,大模型的这种涌现能力其实非常类似于复杂系统中的相变现象。例如,在一个网络中,如果我们不断地往网络上随机地加边,网络就会在连边数突破某个阈值的时候,突然相互连接形成一个大的联通集团。如下图:
图中,p为随机网络中的连边密度,g为最大联通集团的规模大小。左图展示了,随着连边密度增加,联通集团的变化情况。在p=0.45左右的时候,会发生突变,即最大联通集团的规模会突然迅猛增长。右图展示了网络整体的连通性(可以理解为就是最大联通集团的规模)随网络连边概率的变化情况。其中pc即是临界相变点。
AI 大模型的涌现能力可能可以用网络渗流(Percolation)模型来加以解释。其中,网络的规模就对应了连边概率,诸如 in-context 这样的能力就对应为最大联通集团。所以,神经网络的规模在突破一定的阈值之前,它的各种表现效果都接近随机,但是一旦规模超过该阈值后效果将会大大提高。这种涌现能力是一种量变引起质变的飞跃。
另外可能可以用渗流现象加以解释的就是大语言模型的思维链(CoT):对于长推理,大语言模型也是把它拆成一步一步来完成的,而每一步都有一定的正确率,但只要有一步做错,最后的结果就是错的,就好比一连串乘法中有一个乘数是0。在小规模阶段,虽然随着规模增长每一步的正确率都在提高,但把所有步都做对的概率还是极低。只有训练规模到了某个阈值,最后结果的正确率才一下子提升了上来。这也能很好解释为什么像思维链这样的技术能很好地提升涌现实验的效果。
大语言模型的规模法则
与许多复杂系统一样,大语言模型也遵循着规模法则(Scaling law),也就是它的各项宏观指标会形成两两的幂律关系。论文《神经语言模型的规模法则》包含了对交叉熵损失下语言模型性能的经验缩放法则的研究,重点是Transformer架构。在这篇论文中,可以看到语言模型性能与模型大小、模型形状和计算预算之间的关系。这些关系可用于计算我们要训练的固定大型语言模型的最佳有效计算预算,或者反之亦然,以导出给定固定计算预算的最佳有效模型(在模型大小和形状方面)。其中的规律与大语言模型有密切联系,大语言模型可以作为论文中的大样本案例拥有更加良好的表现。
论文题目:Scaling Laws for Neural Language Models
论文地址:https://arxiv.org/pdf/2001.08361.pdf
参看「AI+Science读书会」麻省理工学院(MIT)物理系博士生刘子鸣关于大模型神经标度律的分享:Science for LLM and LLM for Science https://pattern.swarma.org/study_group_issue/446
从已有实验中可以看出,测试损失随模型大小、数据集大小和用于训练的计算量呈幂律变化,有些趋势超过了7个数量级。这意味着存在着简单的方程控制着这些变量之间的关系,并且这些方程可以用于训练非常大的语言模型的最佳有效配置。简单的幂律方程也可以控制过拟合对模型与数据集大小的依赖性以及训练速度对模型大小的依赖。这些关系允许我们确定固定计算预算的最佳分配。更大的模型具有更高的样本效率,因此最佳计算效率训练包括在相对少量的数据上训练非常大的模型,并在收敛之前显著停止。进一步,这些规模法则将应用于具有最大似然损失的其他生成建模任务,可能也适用于其他设置。为此,在其他领域(如图像、音频和视频模型)上测试这些关系将是很有研究价值的。
人们在解释各类复杂系统中的规模法则已有丰富的经验,那么这些经验是否也能迁移到大语言模型呢?让我们拭目以待。
>> 探索 AI 和自然科学相互促进的新范式,关注「AI+Science」读书会:
所谓的复杂适应系统(Complex Adaptive System,简称CAS)简单说就是指具备适应学习能力的复杂系统,例如生物群落、自由市场、城市都是典型的复杂适应系统,这些系统中的每一个构成单元都具备很强的自学习能力。为什么大模型本身也是一个复杂适应系统呢?根据 Holland 和 Murray Gell-Mann 等人的理论,一个复杂适应系统会在与外界互动的过程中把握和外界交换信息的规律,总结出相应图式(schema),再基于这个图式给出相应的行为,形成新的边界。
例如生物进化,外界环境的变化可能对一个生态系统造成毁灭性打击,但自然选择总会让生物在新的环境中出现新的稳态,即全新的食物网。大脑也是一个典型的例子。不断的学习重塑着大脑的神经元网络,以让大脑可以适应新的任务。即使有剧烈的干扰,比如失明让负责视觉的脑区不再起作用,它也能很快地延展其它脑区,充分利用原本的视觉脑区。比如失明的人听觉一般都比较灵敏。
从生态位到类比思维
在复杂适应系统中,有一个重要的概念,叫做生态位(Niche)。这个概念最早起源于生态学,指的是每一个物种在整个生态系统中都有着独一无二的地位和作用。反过来,如果一个生态位上的物种消失,经过一段时间的演化,该生态位上就有可能“诞生”出一个全新的物种,但是它的功能和原物种极其相似。也就是说,我们可以把整个生态系统看作是一个由各个抽象的生态位(也就是功能)组成的系统,而并非是由具体的物种构成的系统。
在John Holland关于复杂适应系统的经典著作《隐秩序》中就给出了这样的例子:三叠纪海洋中的鱼龙与现代海洋中的海豚在整个生态系统中就占据了类似的生态位。虽然鱼龙与海豚无血缘关系,但在外型和习性上却惊人地相似。鱼龙以头足动物(枪乌贼、章鱼)为食,而海豚也吃这些。另外一个例子,枪乌贼的眼睛和哺乳动物的眼睛具备类似的特征,但是它们却出自完全不同的组织。
在商业世界中,我们也能经常看到类似的现象。例如,中国互联网与美国互联网基本处于两个相对独立的世界,但是两个生态系统中都有类似的产品,例如Google与百度都提供搜索引擎;微信与Facebook都提供社交服务;微博与Twitter功能类似。可以说,对于互联网生态来说,这些产品占据了类似的生态位。
其实这种生态位的相似性非常类似于语言之中的类比现象。如果我们将一个词所表达的概念看作是一个物种,而人类整个语言所起到的功能性作用看作是一个生态系统,那么每个概念也就会具有一个类似的生态位。这也就是为什么不同语言都会存在着对抽象数字1,2,3进行表达的特殊单词。这一现象,在语言中被称为类比。
现代的基于预训练的语言大模型本质上就是建立在各个词汇彼此之间的类比关系而进行语言理解的。比如,我们可以利用一个非常浅层的模型(CBOW或Skipgram)来根据一句话中的上下文预测下一个单词,这就足以训练出令人叹为观止的词语之间的类比能力。
论文题目:Efficient Estimation of Word Representations in Vector Space
论文地址:https://arxiv.org/abs/1301.3781
也就是说,表示男人和女人的词向量彼此相减得到的差向量,是与表示国王和王后的词向量彼此相减得到的差向量非常接近的。这说明,在整个语言体系中,国王相对于王后相当于男人相对于女人。国王和王后的关系可以类比为男人和女人的关系。王后这个词在王室成员这个具体的生态系统中起到了和女人这个词在更大的人物角色这个生态系统中类似的生态位。
人工智能专家、《GEB》作者侯世达(Douglas Hofstadter)和他的学生梅拉妮·米歇尔(Melanie Mitchell)曾一直关注如何让机器具备类比推理能力的问题。侯世达甚至认为类比是人类伟大创造性的核心机制,在他的《概念与类比》一书中详细介绍了关于类比的研究。
梅拉妮·米歇尔曾在《复杂》这本书里提及这样一个抽象的问题:如果abc变成abd, ijk应该变成什么呢?我们不妨问问ChatGPT:
很遗憾,它并不能直接类比出一个答案来,一些略微的提示也不足以让它把握住规律,生成图式。这对于人类来讲应该是件很简单的事,自然我们会想到它是要把第三个字母换成字母表中下一个字母,所以应该是“ijl”。当然类比不是严格的论证,我们也不能证明答案一定就是“ijl”,但人类天然的类比与想象的能力,外加关于字母表的知识,让我们迅速找到这个合适的答案。给不出答案或者给出其它答案的人类很可能都在历史中被淘汰掉了。那是否ChatGPT只是暂时没有联想到关于英文字母表的知识呢?
果然ChatGPT给出了我们想要的答案。但读者可能会怀疑,这提示也太明显了,ChatGPT也太笨了,几乎是把解题步骤全告诉它了才给出答案。那我们再升级难度,看ChatGPT是不是真的学扎实了。
当给出“xyz”的时候,ChatGPT很自然地使用了字母表循环这一假设,和大多数人的反应一样。但难度更高的“kji”又不会了。此时需要它能够自动发现字母串的顺序反了,然后构建新的图式。但也不需要我们再提供额外的知识,只要再重复一遍之前出现过的条件,就有神奇的效果出现。
在正序的字母串中替换第三个字母为字母表中的下一个字母,在逆序的字母串中就要替换第三个字母为字母表中的上一个字母,这是ChatGPT能够自动把握的规律。此时如果再考察“mrrjjj”该怎么对应,就是对ChatGPT极难的挑战了。
如果多一些提示提及字母表,ChatGPT 不仅能给出这个问题的答案,还能类比出“xyz”→“xya”,“kji”→“kjh”,但对于“mrrjjj”的类比就还需要更多的提示。
这个实验告诉我们,实际上ChatGPT这种大语言模型离真正掌握做类比推理的能力还有一定的距离。这里问题的关键还是每一个符号所在的“生态位”实际上是一个很大的功能集合。例如在上面的例子中,每个字母背后其实都暗藏着一个字母顺序以及逆排序等等这样的关系集合。简单的字母尚且对应着很多隐藏的关系集合,那么更复杂的事物背后的关系空间则可能更大。然而,问题的麻烦之处就在于,所有这些关系都是隐式存在的。而且,很多关系还是隐藏在物体属性的背后。
近期发展的数学理论范畴论认为,一个事物的定义本身就应该由它与其它对象的所有关系来决定,而并非由这个事物的内部构成来定义。因此,未来的类比推理研究以及生态位等概念有可能都由范畴论来定义。
从水桶链算法到梯度反传算法
现在,说到机器学习,我们就会联想到神经网络。但实际上早在上个世纪90年代的时候,最流行的机器学习算法并非神经网络,而是 John Holland 提出来的遗传算法(Genetic Algorithm,可参考《自然与人工系统中的适应》)及其扩展:分类器系统(Classifier Systems)。遗传算法是通过在计算机中再造一个由大量01编码串构成的生物种群模拟大自然的进化,让适应度高的物种自然而然地获得更高的繁殖机会,而让适应度低的物种自然淘汰。
然而,简单的遗传算法只能够解决函数优化、组合优化等问题,却很难解决机器学习问题。于是,Holland 又开创性地提出了基于遗传算法和水桶链算法的分类器系统。
论文题目:Classifier Systems and Genetic Algorithms
论文地址:https://www.cs.us.es/cursos/ia2-2012/trabajos/BucketBrigade.pdf
如图所示,一个分类器系统是由大量分类器构成的,每个分类器对应一条规则,形如if 001### then 110111。这里的”#”表示的是通配符,即它既可以代表0又可以代表1。于是,每个分类器都在实时地监测由 Input 和 Message List 中的 01 字符串信号,如果找到了if部分能够匹配上的字符串,则该分类器就会被激活,于是它的执行(then)部分的01串就会被发布到 Message List 之中,从而等待着激活其它的分类器。每个分类器有一个被分配的信用值(Credit),它是对该分类器的评估,当多个分类器都可以处理一条激活消息的时候,则系统会让信用值最高的分类器产生真正的输出(Output)到环境中去。所有的分类器会被遗传算法优化,从而进行适应性调节,这就让系统具备了自动从环境中学习的能力。
对于简单的分类任务,上述分类器系统可以工作得很好。不过对于很多复杂任务,往往不是一条简单规则能描述清楚的,如果规则过于复杂,那么潜在的搜索空间将庞大得难以想象。所以Holland认为,可以把一个复杂任务进行拆解,每一步用一个简单规则来完成,许多规则串在一起,让消息从输入开始,一直传递到输出,再根据外界反馈来获得奖励。然而,当传递链条过长的时候,如何对一条消息链上的所有分类器分配信用值则成为了一个麻烦问题。Holland于是开创性地提出,可以用自由市场买卖的隐喻,从而构建了水桶链算法(bucket brigade algorithm)。
Holland将整个分类器系统比喻为一个自由买卖的市场,每个分类器产生的新消息就比喻为一种商品,而一个长长的被激活的分类器链就相当于一条长长的产品生产链。于是,信用就变成了这些分类器手中的货币,可以对产品进行购买。也就是说,当一个消息可以激活多个下游分类器的时候,这些被激活的分类器可以通过出价多少而竞争购买那条消息。购买得到消息的分类器可以被进一步激活,于是它可以进一步生产新的产品——消息。最后,如果一个分类器产生的系统被输出到了环境,并成功地获得了正向的奖励,则该分类器会获得一笔可观的信用值(货币)。整个人工智能系统就像个纷纷嚷嚷的交易市场,盈利能力强的分类器就会被保留下来,构成强大的供应链,一旦有薄弱环节就会被其他分类器替换下去。
熟悉神经网络的读者不难看到,其实整个水桶链算法像极了今天工业界大量使用的梯度反传算法(Backpropagation algorithm)。
我们不妨也把神经网络比喻成一个自由市场,每个神经元就是一个小商贩,它所生产的产品就是传递给下一层各个神经元的“激活”。这样,从输入开始,这些“激活”一层层地往下传递,直到输出,便完成了分类的过程。其实整个神经网络的前馈过程与分类器系统消息激活的过程非常接近,只不过神经网络中的这些神经元不能像分类器那样乱激活,只能按照层次严格地排好,并只能激活临近层次的神经元。
当神经网络产生了输出之后,反向传播算法就会运行,将“错误”一层层地反向传递给所有神经元,并纠正它们的表现(严格说,应该是神经元上的权重)。这个误差反向传播的过程也就对应了分类器系统中的信用通过自由买卖来进行分配的过程。当然,二者的区别还是非常显著的,误差反向传播算法是建立在误差的梯度基础上的,并可以通过自动微分技术(Automatic Differentiation)自动进行。而分类器系统中的信用分配则是按照两个分类器的匹配程度以及遗传算法导致的优胜劣汰而定,与自动微分比起来,则显得效率低下了很多。
论文题目:Automatic differentiation in machine learning: a survey
论文地址:https://arxiv.org/abs/1502.05767
尽管迄今为止,人们并没有在真实的大脑中找到误差反向传播的生物学基础。但是,实际上,根据神经微分方程(Neural ordinary differential equations)和最优控制理论,误差反向传播算法其实就等价于动态规划方法,它是最优化与演化路径相关的目标函数最合理的方法。
论文题目:Neural Ordinary Differential Equations
论文地址:https://arxiv.org/abs/1806.07366
我们可以系统性地对比John Holland的分类器系统和当今流行的前馈神经网络,如下表:
表 1 以复杂适应系统视角对比分类器系统与神经网络
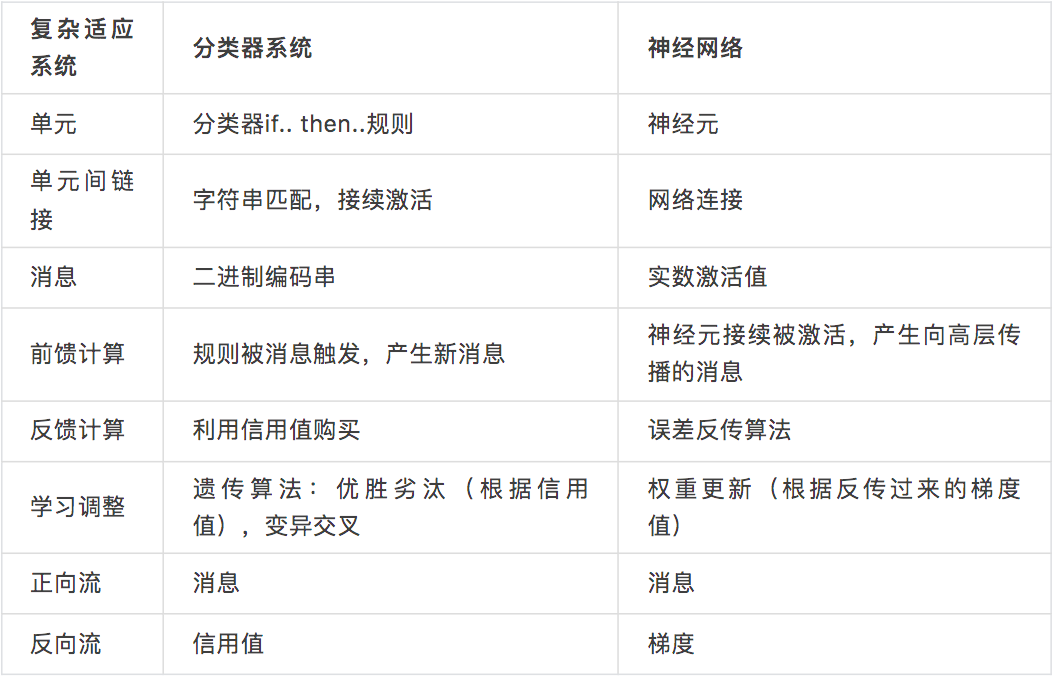
尽管二者存在着差异,但是分类器系统与神经网络的相似性还是非常显著的。这二者本质上都实现了一个两个互为反方向的流动过程。一个是正向的消息接续激活的信息流,这就是神经网络的前馈计算过程以及分类器系统的消息接续激活的过程;另一个则是从输出到输入的流,这就是神经网络中的反向传播的梯度或误差,以及分类器系统中的信用值。这种双向“对冲”的流动才是一个复杂系统产生学习适应能力的本质。
其实,几乎所有的具备学习适应能力的大规模复杂系统都具备这样的双向“对冲流”特征。比如,我们大脑中的学习适应过程就是神经元激活的正向信息流,和由多巴胺等激素控制的反向评价流共同“对冲”而实现的。在人类组织中,前向的流动是组织成员接续的决策而产生的执行/行动流,反向的则是对决策进行评价的评价流,二者构成“对冲”,从而对组织结构和组织成员进行调整,如下图所示。
从抽象的“双向对冲流”的视角理解复杂适应系统的好处,是可以在更加底层的角度把握住各类学习系统的本质;其次,可以在这种抽象层次上建立起各类不同学习适应系统的类比关系,从而可以将一个领域的知识平移到另一个领域上去。例如,我们是否能够根据误差反传思想,或动态规划思想来设计人类组织中的评价机制?或者,我们甚至有可能站在“双向流”的视角,改进并超越现有方法(例如反向传播算法),让学习优化变得更加高效。
我们同样可以从范畴论的视角对双层流模型进行抽象以表示一般的具有适应学习能力的复杂适应系统。下面这篇文章用范畴论的语言将神经网络中误差反向传播算法进行了泛化,这也许可以帮助我们更加系统性、一般性地理解双向流系统。
论文题目:Backprop as Functor: A compositional perspective on supervised learning
论文地址:https://ieeexplore.ieee.org/document/8785665
总结来看,现在已经在各个领域大展身手的AI大模型可以被我们看作一个复杂适应系统,这个特殊的系统展现出了一系列复杂系统常见的现象规律,例如涌现现象、规模法则等等。因而,AI大模型有可能成为复杂科学可以大展身手的一个领域。一方面,我们可以借助现有的分析工具,例如网络分析、动力系统理论、混沌、分形等理论,来理解神经网络动力学及其学习过程;另一方面,对于只有大模型才能展现出来的涌现能力、规模法则现象,则可能可以通过复杂系统的相变理论等进行深入理解。进一步,如果站在复杂适应系统的视角,我们还可以将复杂AI大模型类比为类似生态网络的复杂适应系统,从而站在更高抽象的层次理解生态位、类比推理,以及普适的适应学习原理。其中,范畴论有可能为我们提供高维度的数学工具加以抽象描述。
对于AI研究者来说,采用复杂科学相关的研究手段:非线性动力学、复杂网络、统计物理、复杂适应系统、范畴论等等工具,有助于我们站在普遍系统的视角更好地看待AI大模型。它一方面可以帮助我们在整体性角度理解AI大模型的工作基础,特别是针对涌现、规模法则等现象的深层理解,另一方面也可以帮助我们更好地改进模型提供洞察和帮助。除此之外,这些理论工具也有助于我们构造可解释性的AI模型。
对于复杂系统科学领域的研究者来说,长久以来,人们很难在复杂科学领域取得重大突破,这有相当一部分原因是真实复杂系统很难进行观测及重复实验。于是,人们通过构建计算机模型来替代真实的复杂系统。而这些模型又因为过度简化,或者并不能完成实际任务,从而导致研究工作意义不大。现在,有了可以执行复杂任务的AI大模型,复杂科学家们便可以有了全新的理想研究对象。通过研究分析大模型可以获得关于复杂的网络动力学及其适应演化的第一手材料,从而有助于从中提炼出一般性的普适规律。由于模型高度的可控性,我们可以通过数值计算的方式完成实验,从而大大降低了我们研究复杂系统的成本。其次,由于AI大模型可以解决很多实际问题,对模型的理解和优化也有助于实际问题的解决。
接下来我们讨论第二部分,用大模型辅助复杂系统的研究。
我们不仅可以将AI大模型视为复杂系统来加以研究,还可以以这些AI大模型为中间跳板,从而间接理解真实世界的复杂系统。这样做的好处是,我们首先可以将真实复杂系统的数据压缩成一个AI大模型,有了这个大模型后,我们就仿佛拥有了一个“玩具”,从而通过各种模型调试,来认知大模型背后真实复杂系统的概念。当然,这样做的前提是,AI大模型不仅仅能够拟合真实复杂系统的数据,还能够把握住真实的因果规律。
笔者所在的研究组就在从事这样的工作,我们将这一研究方向称为“复杂系统自动建模”。感兴趣的读者,可以参考文章《从图网络到因果推断,复杂系统自动建模五部曲》。在此不再赘述。
若想以AI大模型辅助我们对真实复杂系统进行研究,一个重要的关键环节就是从大模型中提炼出人类能够理解的知识。那么,知识又是怎样在大模型中存储的呢?
我们还是以大语言模型为例来展开讨论。在大语言模型训练过程中,模型的参数会根据输入文本适应性改变,从而涌现出各种能力。但是,这种能力究竟是如何产生的,又存储于人工神经网络的什么地方呢?
为了回答这个问题,我们可以借鉴人类大脑的认知机制。在人类学习知识的过程中,儿童既从与真实世界的交互中学习世界模型,又通过阅读、听取等媒介获取知识。这些经验和知识最终被存储在大脑的神经网络中,形成了我们对世界的认知和理解。
大脑中的知识
让我们先来看看“猫”这样的概念是如何从我们的头脑中“涌现”出来的。不管是人类大脑还是人工神经网络,都是通过类似的自下而上的过程来获取知识与概念。以人脑视觉处理为例,现有的理论认为大脑视觉皮层V1区的神经元只能检测微小的特征,例如线条、边界等。V1区的神经元将处理后的特征传递到V2区,在V2区将简单特征聚合成更复杂的特征,例如角点或弧形。通过这种方式,我们可以从简单特征到复杂特征再到识别出整个物体,比如“猫”这样的动物。
计算机科学家和神经科学家杰夫·霍金斯(Jeff Hawkins)在《千脑智能》一书中提出的千脑理论认为,大脑中的新皮质在对世界进行建模,学习若干关于世界知识的世界模型,并基于该模型进行预测,这一点和认知神经科学领域的自由能原理主动推理理论不谋而合,Yann Lecun在《A Path Towards Autonomous Machine Intelligence》中也有类似的论述。此外千脑理论认为单根皮质柱可以学习数百个复杂的物体但受到输入的限制,例如一根视觉皮质柱无法学习旋律的模型。该理论认为新皮质并非使用层次结构将特征聚合成所识别的物体,而是使用层次结构将简单物体聚合成更复杂的物体。尽管千脑智能理论的正确性仍然存在争议,但是人类大脑通过对不同类型的感觉输入信号进行分化,从而产生不同功能的脑区,这一点已经得到广泛的科学认可。
>> 探索自由能原理、强化学习世界模型、意识理论等话题,关注最新的「自由能原理与强化学习」读书会
此外对于单个模态的功能而言也存在分化现象。以语言功能为例,不同脑区的神经元可能负责不同的语言功能,人类大脑中的语言区域可以分为布罗卡区和韦尼克区。经典模型认为布洛卡区位于左半球额叶的后下方,主要掌管言语的运动,若布洛卡区受损就导致运动性失语症。威尔尼克区在颞叶上方、靠近枕叶处。主要与理解口头语言有关,威尔尼克区受损将引起听觉性失语症。
语言模型通过学习大量的文本数据,不断调整自身的参数,从而逐渐学习到文本的语言规律和语义信息。这些规律和信息被存储在人工神经网络的连接权重中,形成了语言模型对文本的理解和生成能力。那么,大语言模型所学到的知识是否也存在类似大脑的层次以及分化现象呢?
语言模型中的知识
Mathematica以及Wolfram|Alpha 的发明者Stephen Wolfram做了一个简单实验,对训练好的GPT-2模型进行了分析,他通过对attention block中的全连接网络参数矩阵进行移动平均后,将其可视化,如下图所示:
 图20. 语言模型中网络参数矩阵移动平均后的可视化
图20. 语言模型中网络参数矩阵移动平均后的可视化
语言模型中网络参数矩阵的可视化呈现出一些有趣的类似斑图的形态。虽然这些“斑图”并不能直接告诉我们“知识”具体位于何处,但是它们的存在却表明了神经网络中的知识可能存在某种结构和模式。
最近的研究表明,大语言模型可以学习各种层次的语言学知识,其中包括浅层语言知识,如词汇、词性和句法等,这些知识存储在Transformer模型的低层和中层。同时,抽象的语言知识,如语义知识,则广泛分布在Transformer的中层和高层结构中。
知识神经元
在论文《Knowledge Neurons in Pretrained Transformers》中,作者引入了知识神经元的概念,对Transformer中的事实性知识(可以被判定为真或假的信息)存储进行了初步研究。通过对预训练语言模型BERT进行填空测试来检查知识神经元。给定一个关系事实,使用积分梯度法(Integrated Gradients)进行知识归因 (Knowledge Attribution)来识别表达该事实的神经元,实验发现这些知识神经元的激活与它们对应的事实表达呈正相关。
图21. 知识神经元工作原理
除此之外,近期发展的一些神经网络归因分析方法,如《Neural network attributions: A causal perspective》,还有一些有关可解释的人工智能技术都为我们进一步解读神经网络提供了很好的帮助。不难设想,如果假以时日,ChatGPT这样的大模型将可能具备自我归因,自我解释的能力,从而不仅能够很好地辅助人类解决各类复杂系统的问题,也可以为人类提供各种不同的领域知识。
>> 神经科学和人工智能如何相互启发?关注「NeuroAI」读书会:
NeuroAI 读书会启动:探索神经科学与人工智能的前沿交叉领域
复杂科学的一个奋斗目标就是找到各种不同复杂系统背后的通用性规律和方法。例如,规模法则就是跨越不同复杂系统的一种通用法则,或唯象规律;再如,涌现则是不同复杂系统所共用的一种抽象概念;网络分析则是可以横跨不同学科的普遍的分析方法。对于这些跨领域的、通用的知识提取正是复杂科学追求的目标。然而,目前的复杂科学尚没有发现跨越不同复杂系统的普适原理的存在。那么,AI大模型能否帮助我们实现这一点呢?不难发现,其实对这一目标的追求的前提就是AI大模型要能够跨领域的解决问题,这也恰恰是通用人工智能(AGI)真正的终极目标。
要实现这一目标,首先第一步就是要获取各种不同复杂系统的传感数据,而这些数据有的是以时间序列的方式存储,有的是以图片的方式存储,有的则是用文本描述的方式存储的。因此,AI系统首先应该先具备一个能够处理多模态数据的数据预处理层。其次,当AI系统融合了多个模态的数据之后,还应能完成更高层次的推理。这不仅需要通过深度的网络才能实现,而且还需要有一个通用的与底层输入数据无关的通用接口,从而将抽象的推理层和浅度的感知层加以分离。最后,如果能够融合可解释性的人工智能,则系统还应能在更深的层次给出跨领域的抽象知识。也许,这些知识正是我们梦寐以求的复杂系统的通用原理。
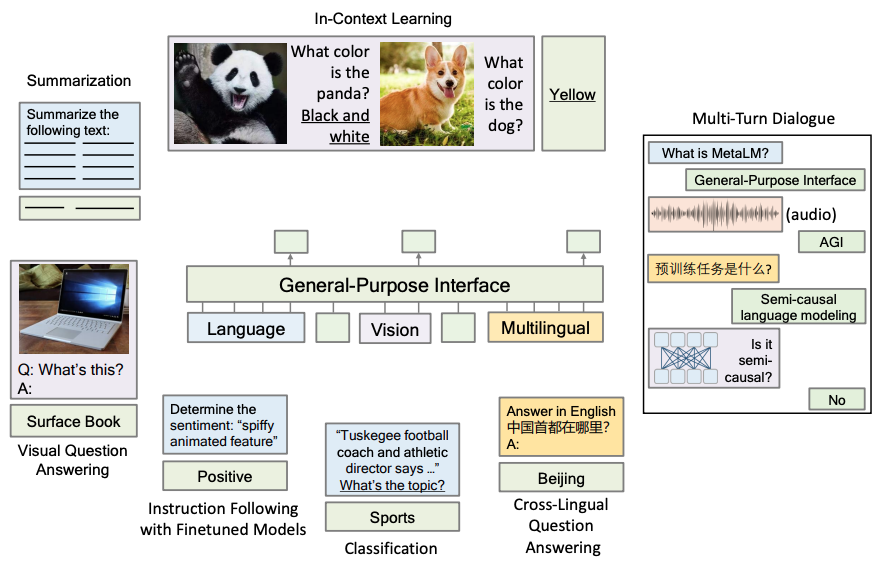
图22. 综合语言和视觉两种模态的大模型AI系统
尽管很多AI研究者并不关心复杂科学的发展,但可喜的是,AI研究者们正在坚定不移地向通用领域进军。例如,微软最近的一篇论文《Language Models are General-Purpose Interfaces》正在尝试能够综合语言和视觉的通用目的接口,如上图所示。该系统不仅能够处理多模态的数据,而且还能够尝试解决不同形式的各种领域的问题,从而提供一个通用目的接口。尽管,这种通用领域中的大模型才刚刚起步,但是未来的发展将不可限量。
总结来看,有了AI大模型,我们便可以对复杂系统展开更加深入的研究。首先,我们可以将AI大模型看作是真实世界中各类复杂系统的通用压缩器,从而将这些复杂系统生成的数据压缩进AI大模型中;其次,我们便可以通过研究这些AI大模型从而尝试提取它所建模的真实复杂系统中的知识,当然这需要归因分析、可解释人工智能技术的发展;最后,未来的通用AI大模型将有可能打通不同领域之间的壁垒,从而自动化地提炼跨领域的通用知识存储到大模型的深层网络中。而进一步,调用可解释人工智能等技术,我们便有可能从AI大模型中提炼出人类能够理解的复杂系统背后的深层次、通用的规律了。
这篇结合多篇经典论文的学习路径在“集智斑图”网站首发,欢迎扫码登录集智斑图,获取完整学习路径。
https://pattern.swarma.org/article/224




集智学园最新AI课程
张江教授亲授:第三代人工智能技术基础
本课程面向具有一定理工科背景和编程技术基础的学生,全面介绍基于大数据技术驱动为主的人工智能技术的最新进展,包括但不限于:神经网络、深度学习、强化学习、因果推断、生成模型、语言模型、面向科学发现的AI等前沿领域。希望学员能够在本课程的学习过程中了解数据驱动的人工智能最新方法、技术和前沿发展情况,同时通过一定的课程项目实践,能够具备利用人工智能解决复杂问题的实操、编程能力。课程目前已全部上线,扫码可报名课程。
集智俱乐部长期深耕复杂系统与跨学科研究,在网络科学、系统理论、混沌科学等经典领域持续策划精品课程,同时也追踪因果科学、深度学习、复杂经济学、生命复杂性、社会计算、AI+Science、大模型、神经科学、城市科学等交叉前沿。汇集了大量的探索者,包括教授、硕博、工程师、创业者等等。
为了帮助有学习需求的朋友夯实学科基础,帮有科研需求的朋友深入前沿交流,我们开放了1年制和2年制的集智学园VIP计划。VIP用户可以深度参与集智俱乐部社区,并在会员期内解锁集智学园全站课程权限。






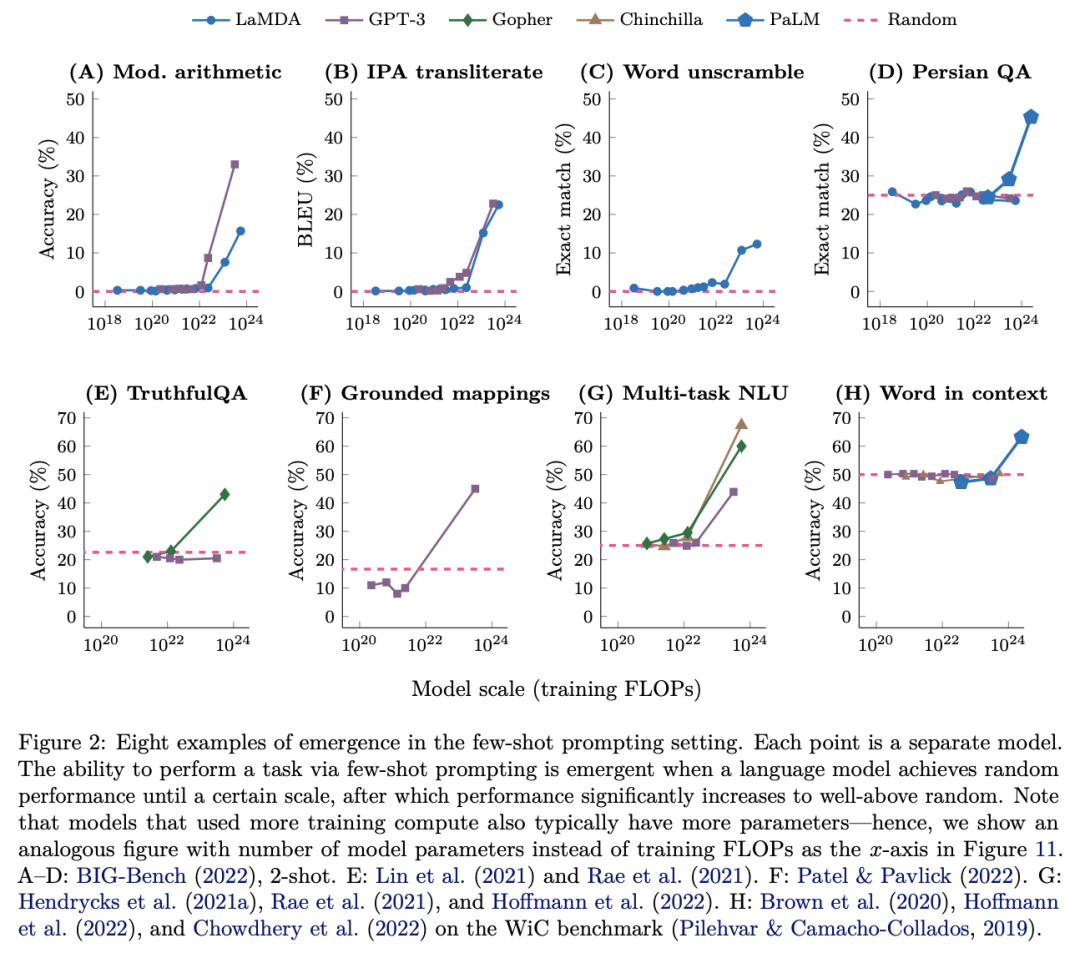
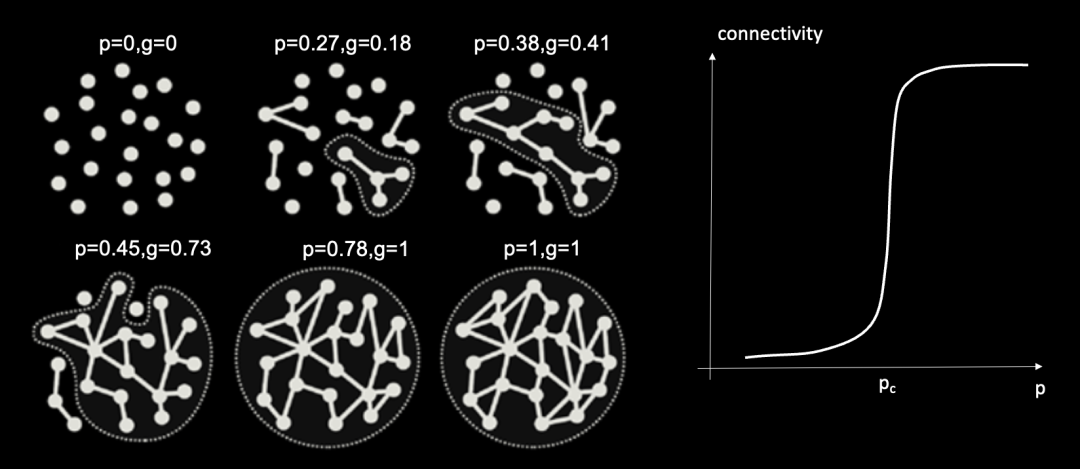
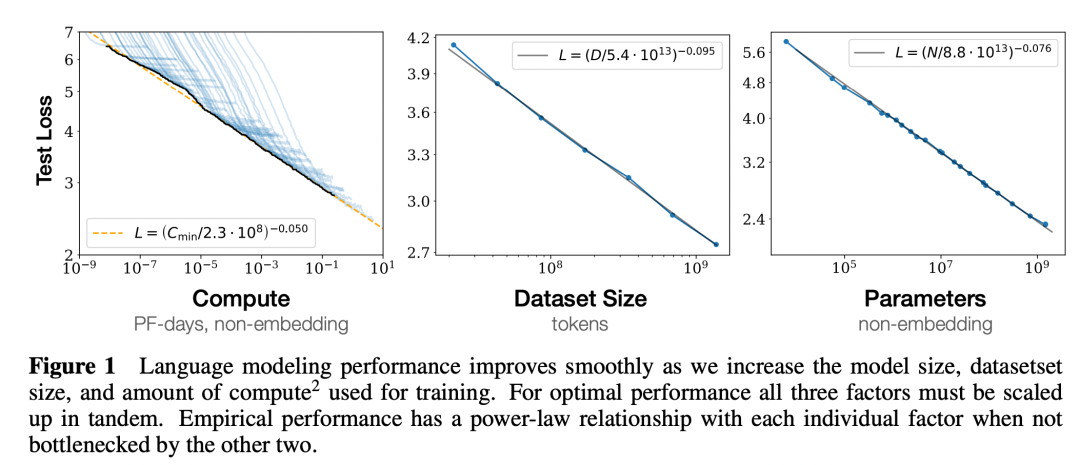



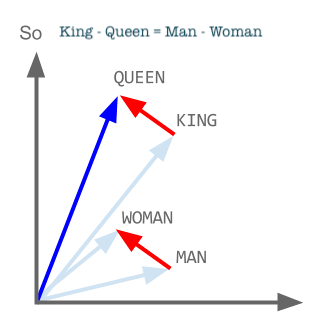



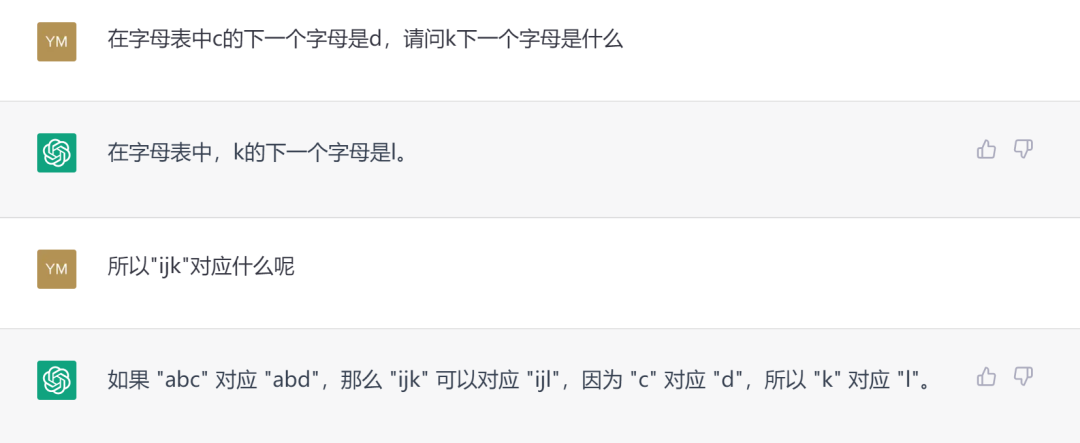


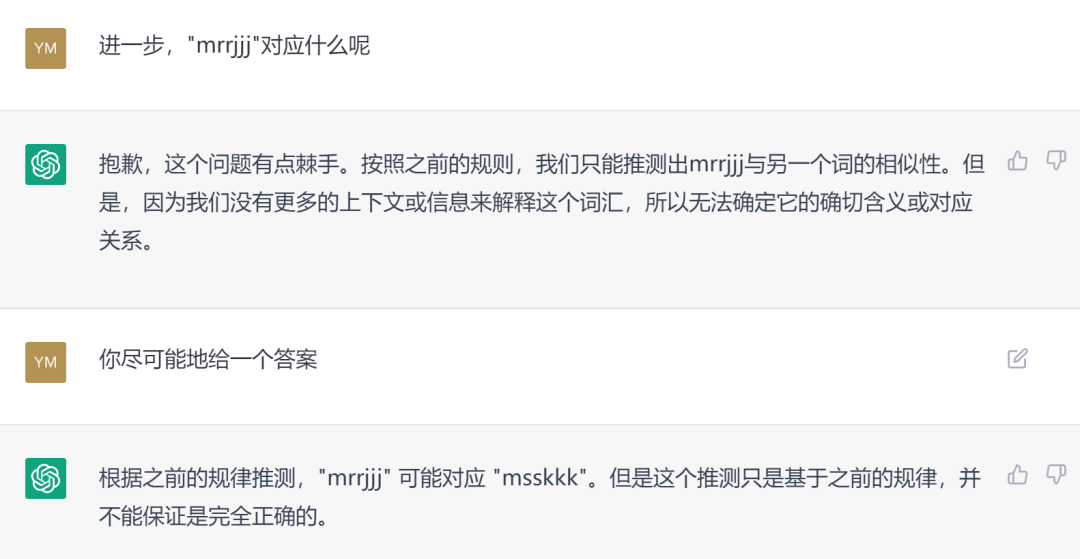
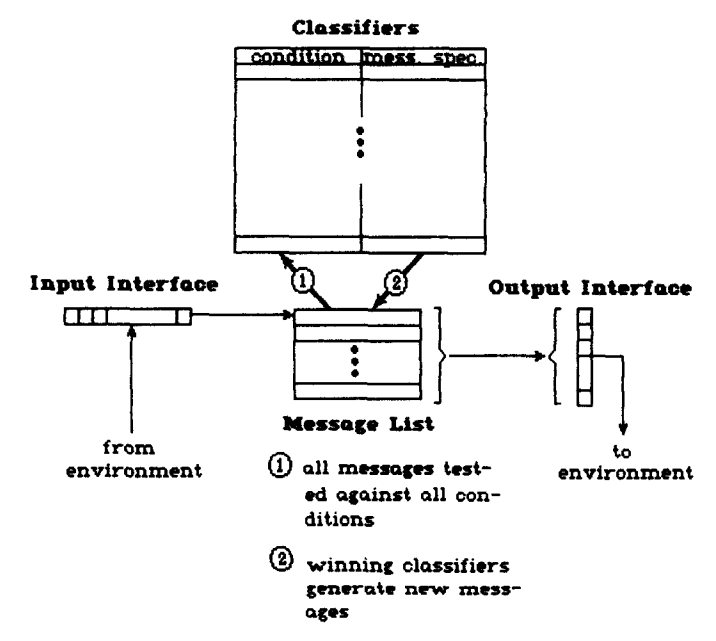


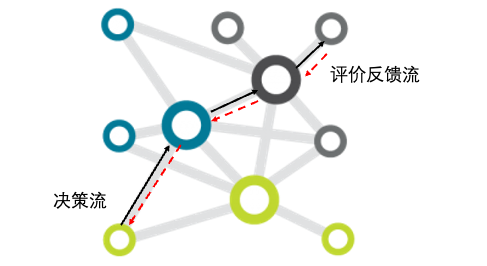


 图20. 语言模型中网络参数矩阵移动平均后的可视化
图20. 语言模型中网络参数矩阵移动平均后的可视化