第三次科学范式转移？｜新春特辑

导语

科学的第一次重要转变被称为“牛顿范式”，牛顿发明了微积分和经典物理，教会了我们如何思考；第二次重要转变是20世纪初发现的量子力学和海森堡不确定性原理，是从经典到量子物理学的转变。著名理论生物学家和复杂系统研究者考夫曼（Stuart A. Kauffman）等人认为，我们正面临科学的第三次范式转移——演化的生物圈是牛顿范式之外的世界。生物圈是已知宇宙中最复杂的系统，我们不能用数学来推导预测生物圈的演化过程，一个不断演化的生物圈是一个自我构建的涌现过程，是涌现而非工程。

跨尺度、跨层次的涌现是复杂系统研究的关键问题，生命起源和意识起源这两座仰之弥高的大山是其代表。为探索复杂系统的涌现规律，集智俱乐部组织了「因果涌现」共四季、「生命复杂性」、「自生成结构」等系列主题读书会，欢迎对这一领域感兴趣的朋友持续关注。新的一年，让混沌涌现新生，我们继续一起复杂！

研究领域：复杂系统，自然演化，涌现，自上而下因果，科学范式转移

Stuart A. Kauffman，Andrea Roli | 作者

Dialogue with nature | 译者

小木球 | 审校

梁金 | 编辑

论文题目：

A third transition in science?

论文链接：

https://royalsocietypublishing.org/doi/10.1098/rsfs.2022.0063

摘要

1. 简介

2. 生物圈不可推导式的历时演变（diachronic evolution）

3. 集合论不可逾越的极限

4. 第三次转型：我们已经超越了牛顿范式

5. 综合功能的演变：涌现不是工程

6. 结论

摘要

自牛顿以来，经典物理学和量子物理学都依赖于“牛顿范式”（Newtonian paradigm）。“牛顿范式”系统的相关变量是确定的。例如，当我们要确定经典粒子的位置和动量，需要先构建连接这些变量的微分形式的运动定律。例如牛顿的三个运动定律，通过定义边界条件以创建所有可能变量的相空间。然后，当给定了任意初始条件，对运动的微分方程做积分，就可以在预设的相空间中产生一个确定的轨迹。牛顿范式的基本原则是，构成相空间的一系列可能性总是可以提前定义和确定的。

但是，对于任何一个生物圈（biosphere）中持续更新其适应性的历时演化（diachronic evolution）时，牛顿范式就会失效。活细胞通过可遗传变异和自然选择进行演化，适应性地构建宇宙中全新的可能性。对此，我们既不能定义也无法推导出演化的相空间（phase space）来。我们无法用基于集合论的数学来处理这件事。我们也不能为生物圈中不断出现的更新适应性的历时演化写出微分方程或求解出来。演化中的生物圈是牛顿范式之外的世界。目前来说，还没有找到包含所有事物的万物理论。我们面临的科学的第三次重大转变，超越了牛顿物理学所呼应的“万物皆数”的毕达哥拉斯式梦想。我们开始理解，一个不断演化的生物圈展现出的创造力的来源：是涌现的（emergence），而不是工程的。

1. 简介

我们认为，在牛顿身后三个世纪的今天，我们正处于科学上的第三次重大转型。本文作者希望阐明这一转型的证据及这一转型的必要性。我们还希望阐明，演化的生物圈将为这一转型带来意想不到的视野。我们的阐述基于诺贝尔物理学奖得主安德森（P.W.Anderson）在1972年的重要论文《多者异也》（More is different）[1]。这篇论文近期被 Nature Physics 庆祝发表五十周年[2]。（参看：《多者异也》五十年：追随安德森的脚步）

科学上的第一次重大转型可以归因于牛顿，他发明了微积分和经典物理。毫不夸张地说，牛顿教会了我们如何思考。因此我们将第一次重大转型称为“牛顿范式”（Newtonian paradigm）[3]。

（1）“牛顿范式”的第一步是，找到相关变量。在物理学中，相关变量通常是位置和动量。

（2）写下这些相关变量的运动规则（laws of motion），通常是采用常微分方程或偏微分方程的形式。这些方程可以是确定性的（deterministic），也可以是随机性的形式（stochastic）。

（3）定义边界条件，从而定义系统粒子的位置和动量等相关变量的所有可能值的相空间（phase space）。对于相关变量的任何初始条件，对前面写下的关于运动规则的微分方程进行积分，就可以得到相空间中系统的轨迹。牛顿范式的基本特征是，我们始终可以而且必须提前定义固定的相空间。

包括广义相对论在内的经典物理学给了我们 “钟表”（clockwork）宇宙，它将以决定性的方式展开。由此，自然神论中的上帝不再能够创造奇迹。钟表宇宙使得“偶然性”仅仅是认识论（epistemic）上的。

第二次重大转型莫过于1900年代发现的量子力学[4]和海森堡不确定性原理[5,6]。这些发现加上后来的量子场论，导致了超越经典物理学的转型[7,8]。然而，量子理论仍然安稳地保持在牛顿范式中，因为量子理论也要有预设的相空间，比如Fock空间。因此，当给定初始条件和边界条件，通过薛定谔方程能够给出概率分布的演化，这个系统的演化就是确定性的。在对量子力学的大多数解释中，“偶然性”是本体论（ontological）所定义的[9]。

牛顿范式的巨大威力不仅局限于物理学。生态学（Ecology）经常采用非线性动力学方程来描述物种群落的演化过程。该方程包含了每个物种成员的繁殖率和物种之间的食物网。方程在相关变量预定义相空间中的积分，可能表现出非线性动力系统的极限环、多重吸引子等方面的性质[10]。

我们现在希望把生态学放在一个更广阔的背景下来讨论。生态学处理的是群落中预先定义的一组物种。这些物种提供了相关的变量，因此有了预设的相空间。随着演化时间的推移，物种往来生息。这组物种及其之间相互作用的模式本身也在演化。在生物圈的历时演化中，新的适应性（adaptations）出现，现有的适应性随物种灭绝而消失。生态学可能在一定时间尺度上是有效的，例如当物种不会演化出相关的新特征或失去相关的旧特征时。我们想提出的问题，也是本文的中心问题是：我们是否可以预测或推导系统将出现的新的相关自适应变量和消失的旧的自适应变量。我们能否有充分的预期？我们希望证明那个答案是“不”。

如果我们不能推导出这种不断变化的相空间，那可能是因为我们无法写下或求解运动方程，并推导出这些不断变化的相空间。我们将置身于“牛顿范式”之外。

地球上的生命已经存在了将近40亿年，几乎占宇宙寿命的30%。牛顿范式在生命演化方面的失效，意味着宇宙学演化的主要方面并不在牛顿范式的讨论范围之内。

>> 生命是什么？生命如何起源和演化？关注「生命复杂性」读书会：

读书会详情：生命复杂性系列读书会：从信息和物理视角探索生命的内在逻辑

2. 生物圈不可推导式的历时演变

地球上的生命大约开始于37亿年前。生物圈是已知宇宙中最复杂的系统。新问题的核心在于，我们不能通过推导来预测我们生物圈，或任何一个生物圈的演变过程。演化中的生物圈是一种不断繁衍的结构，而不是一个被推导出来的结论[11-14]。

原因乍看起来似乎很奇怪 [13-15]:

1.宇宙在大约500道尔顿以上是不遍历的[16]（Da全称是Dalton，中文道尔顿，是分子量常用单位，将分子中所有原子按个数求原子量的代数和）。宇宙制造出复杂分子需要的时间非常长，比如200个氨基酸长的蛋白质，需要的时间比宇宙的寿命更长。所以宇宙不会制造出所有可能的复杂分子[13,17]。不同复杂分子的化学和物理性质是不同的，在生物学中，细胞中数以万计的不同分子其功能特性也是不同的。宇宙不是遍历的，因为它不会产生所有可能的复杂分子，大多数复杂的东西确实永远不会“获得存在”的机会。

2. 人类心脏的重量约为300克，结构复杂，其功能是泵血。这么复杂的人类心脏怎么可能存在于宇宙中呢？心脏之所以会存在于宇宙中的根本原因是，基于物理学的生命在演化中随着时间的推移而产生、演化和适应。生命体是一个遵循非平衡过程的特殊组织。生命体是康德式整体（Kantian whole），其部分为了整体而存在，并通过整体而存在。人类当然也是康德式整体，我们的部分为了我们的整体而存在，我们的部分也是通过我们生命的整体而存在。例如心脏泵血，肾脏净化血液，然后在肾的亨勒环（loop of Henle）中制造和排泄尿液。由于我们，作为康德式整体来繁殖后代，而我们的部分，例如心脏和肾脏也在繁殖和演化，以更好地为整体发挥作用。心脏的“功能”是泵血，而不是在心包囊中抖动水。部分的功能是维持整体，部分是整体因果属性的子集[13]。

如果不借助达尔文的自然选择和可遗传变异来研究器官的功能，及其适应性历时演化，我们就无法解释器官在宇宙中存在的原因，例如宇宙中为什么可以存在心脏用来泵血，或肾脏中存在可以净化尿液的亨勒环。

• 选择是一种向下的因果关系（downward causation）。选择作用于整个生命体，而不是其演化中的局部。在不断演化的生物圈中，得以存在的是被选择出来的东西。

• 解释箭头指向上方。整体的选择会改变部分的构成。

更详细地说，康德式整体具有的特性是，部分是为整体而存在，并通过整体而存在。一个简单的例子是一个由九个肽（peptide）组成的自催化集 [13,18]。在这里，肽1催化一个反应，将半片肽2组配成第二份肽2。这些半片肽2是从外源提供的“食物”。同样地，肽2催化形成第二份肽3。依此类推，在一个循环中，肽9催化第二份肽1的形成。整个九肽的集合是共同自催化的。这个集合是一个康德式的整体。这个自催化的物质集合具有以下特性：

• 它是集体自催化的[18]，其中没有一个分子催化自己的形成。因此，这是一个康德式的整体，各部分确实为整体而存在，并通过整体而存在。

• 部分的功能是其维持整体因果属性的那个子集，肽1的功能是催化肽2的第二个拷贝的形成。如果在这样做的时候，肽1会扰动培养皿中的液体，那么这个因果关系的结果就不是肽1的功能 [13,14,17,19]。

• 该系统实现了催化的封闭：所有需要催化的反应在同一系统内都有催化剂。

• 该系统具有最近被认知的强大特性——约束闭合（constraint closure）[12]：热力学功是能量释放到少数自由度上的约束形成的[20]。这些约束构成边界条件。九肽自催化集体系中的肽分子就是物理约束条件，它们约束化学能量的释放：每个肽分子结合下一个肽分子的两个底物，从而降低了活化能，使得化学能量释放到少数自由度上，从而进行热力学作功来结合两个肽段并构建出下一个肽分子。关键在于，肽分子集体构建自身，从而构建了约束能量释放的约束条件，这构成了它们进行自我构建工作的约束闭合[12-14]。

细胞可以说是在自我构建。不断演化的生物圈也在自我构建。而汽车则不具备这种能力，我们必须亲手将其制造出来。生命细胞构成了一种新型的物质和过程组织方式，将热力学作功、催化闭合和约束闭合有机结合在一起。从某种意义上说，这就是人们一直在寻找的“生命力”（vital force），但它并不神秘。因为生命细胞是开放式的热力学系统，能够自我构建，它们会构建出不断更新的边界条件，从而创造出新的相空间可能性。由于边界条件会不断变化，因此会出现新的“相关变量”，从而构成新的相空间。例如，就心脏而言，收缩压、舒张压、心脏血液射出量和血氧含量是现在具有功能意义的变量之一。如果没有新功能的适应性演化，我们又该如何解释这种现象呢？

生物体在演化中的适应性是可供性（affordances），通常通过遗传变异和自然选择来利用。可供性的一个例子[21]是，一个水平的表面为你提供了一个坐的地方。可供性通常指“我能够使用X来达成Y的可能性”。达成可以无需“思维”，而是通过“盲目的”遗传变异和自然选择，例如在心脏和肾升支亨勒环的演化中所实现的[15]。可供性并不是这个世界中的某种独立特征[22]。可供性是与演化中的生物体相关的，对于这些生物体来说，可供性可以通过遗传变异和自然选择被利用或弃用。生物学的自由度是可供性，或是对于演化生物体提供的相关机会。

在演化过程中，通常通过“合并选择”（co-opting）同一器官来适应新的功能。这被称为达尔文先适应或旧用新得（Darwinian preadaptations or exaptations） [23]。

这样的可供性（affordances）或者新的达尔文先适应性的典型例子，被遗传变异和自然选择所占用，包括如下：飞羽，早期为了保暖或作为刷子的功能而演化出来，但是被用于飞行的新功能[24,25]；而晶状体晶状蛋白起源于酶[26]。

在鱼类的一系列演化事件中，鱼鳔的演化是一个很好的例子 [27]。鱼鳔通过调节其内部的空气和水的比例，可以来适配其在水体中的中性浮力。古生物学家认为，鱼鳔起源于肺鱼的肺部。水进入肺的局部区域，使得其成为一个充满空气和水的囊袋，可能由此逐渐演化成了鱼鳔。这就为相同的起源的“事物”——也就是肺——发展了新的用途，从而在不断演化的生物圈中出现了一种新的功能，即鳔在水中的中性浮力。

在演化过程中，通常会出现这种“可利用性”或新达尔文主义先适应性，被遗传变异和自然选择所捕捉。其中典型的例子如飞羽，它们早期演化出保暖或刷毛等功能，但后来被选择而发展出了新的飞行功能。[24] [25] [26]

新的底层问题在于：是否可能，通过从37亿年前开始推导到未来某个时间点（例如从今天起4亿年之后），从而在生物圈的演化中预先陈述所有可能的达尔文预适应性？我们当前的阐述希望表明的是：这是不可能的。

3. 集合论不可逾越的极限

在生物圈的演化中，随着新的边界条件和新的相关变量出现，会出现新的相空间，这些相空间之前没有被预设过。那么现在这些新出先的相关变量是能够被预先设定的吗？我们希望能够展示一个令人惊讶的答案，即“不能”。我们必定会失败，因为我们不能事先计算、预测或推导出由遗传变异和自然选择捕获的新的可供性和相关变量的出现。

我们必定会失败，因为我们不能使用集合论或任何基于集合论的数学来可靠和妥善地模拟适应性作为“可捕获的可供性”的演化出现。这些考虑有些出人意料，重点在于生物圈演化特征对集合论基础的影响。我们强调，我们下面提供的不是数学证明，而是一种概念上的演示。

下面以一个工具使用作为例子，可能会更容易理解。假如在2025年的3月22日，伦敦街头摆放着一个螺丝刀，把它单独或与其他东西一起使用，可以有多少个“用途”呢？（i）拧紧螺钉，（ii）打开一罐油漆，（iii）将门用楔子固定，（iv）刮掉窗户上的灰，（v）作为“艺术品”，（vi）将其绑在木棍上，当作鱼叉来刺鱼，（vii）把这个鱼叉租借给当地渔民并抽取5％的收成，（viii）将螺丝刀靠在墙上，放置用螺丝刀支撑的胶合板，用这个构建的遮雨棚来保护油画……等等。

一把螺丝刀单独使用或与其他东西一起使用的用途数量是一个特定的数字吗，比如说11？用途数量是否是无限的？我们怎么知道呢？现在和未来1000年，螺丝刀的用途数量是“不确定的”或者可能是“未知的”。1690年没有人可以使用螺丝刀来让电路链接短路。必须强调的是，我们无法列举出螺丝刀的所有可能用途，因为我们不仅无法预测螺丝刀的未来可能利用的空间，而且螺丝刀的用途还取决于用户的目标和行动范围。同样的考虑也适用于任何物体，例如发动机的用途。它可以用来制造引擎，作为拖拉机底盘，用来打开椰子等等。

也许我们可以通过列举或演绎来列出螺丝刀的所有用途？这也是不可能的。有四种数学排序尺度：标称、偏序、区间、比率。物体的用途只是一个标称度量，而这些用途之间并没有顺序关系。此外，通常一个物体的特定用途并不能为推导出另一种用途提供依据。因此，物体的不同用途之间不存在“演绎关系”，例如，不可能从引擎可以作为纸张称重砝码的用途中推导出引擎也可以用来敲开椰子。

这些论点也支持在生物圈的历时演变过程中，适应性作为可供性的出现。不断涌现的新的可供性被演化所利用，并以一种不可预测的方式形成了不断更新的生态位和生物适应功能。我们现在要展示的是，我们不能使用集合论来推导生物圈历时演化中不断涌现的适应性[15]。

集合论的第一个公理是外延公理：“当且仅当两个集合具有相同的成员时，它们才是相同的”[28]。但是我们无法证明。螺丝刀的不可列出的用途与发动机块的不可列出的用途相同，因为我们无法一劳永逸地获得物体X的用途。因此，没有外延公理。如果没有外延公理，就无法定义集合。因此，无法建立可靠的集合论。

更糟糕的是，这些影响还涉及基于集合论的数学领域。当无法定义选择函数时，便需要使用选择公理[29]，然而选择公理也无法应用。选择公理等同于“良序原理”[30]，但在未经排序过的X的使用方案中，无法排出序列。

这个论点的一个结果是，当生命演化过程中出现新功能的时候，不可能使用数字。定义数字的一种方式是使用集合论[31]。数字“0”定义为每个元素都是0个的所有集合的集合。在我们的案例中，这相当于“所有只有0个使用的对象的集合”。然而，这不可能以对象、个体和目标为基础[22]。

另一种选择，则是通过皮亚诺（Peano）公理[32]。这需要一个空集和一个后继关系。但我们没有空集。此外，X的不同用法是无序的，因而也没有后继关系。

因此，在所有通过获取可供性而出现的历时适应中，无法出现数字。因此，没有整数，没有有理数，没有像 2+3 = 5 这样的方程。没有方程，因此没有无理数。没有实数线。没有带变量的方程。没有虚数，没有四元数，没有八元数。没有笛卡尔空间。没有向量空间。没有希尔伯特空间。没有X和Y的使用的并集和交集。没有一阶逻辑。没有组合数学。没有拓扑学。没有流形。没有流形上的微分方程。此外，如果没有选择公理，我们不能对我们无法编写的微分方程进行积分和取极限。

以上主张非常重要。因为这证明了，对于出现的新可供性，通过可遗传的变异和自然选择或行为中的有机体在其世界中行动，我们无法使用集合论的数学。这将产生广泛的影响。我们的中心主张是，无法使用基于集合论的数学，“世界不是一个定理”，这个论断已在其他地方发表[15]。基于此，我们得出结论，世界中的生物体不可能是通用图灵机，因此排除了通用人工智能的可能性[35]。这进而使我们考虑到心智是量子的，感性与波函数坍缩相关[36]，正如von Neumann[37]，Wigner和Margenau[38]，Shimony[39]和其他人[40]所认为的那样。

我们能否找到一个正式的数学/逻辑证明来确证我们的论断？我们认为不行。我们的主张与哥德尔的著名定理并不相似。哥德尔的工作完全在数学的形式框架内进行。他从一组公理中证明了会有形式上不可判定的陈述。在目前的情况下，我们不在一个正式的框架内。要想找到我们主张的正式证明，似乎需要使用集合论的数学来正式证明我们不能使用集合论的数学。事实上，我们的主张就是存在着一个庞大的世界，超出了我们可以使用集合论捕捉到的范围。

上世纪70年代以来，对复杂系统的研究分化为两条不同的进路：一条方向，以统计物理为思维范式，分布式涌现为典型现象，非线性动力学为数学基础，伊辛模型和多主体模拟为计算机模型，试图发现复杂系统宏观性质之下统一的简单原则；另一条线路，以哥德尔定理和自指结构为核心，以结构分析为思维范式，在图灵机模型和冯·诺依曼理论为基础构建出模拟人脑的电子计算机之后，掀起前所未有的信息革命。

「自生成结构」读书会以第二条线路为牵引，以“自生成结构”为核心概念建立跨学科共识，通过辨析主体涌现与分布式涌现在复杂活系统形成中的角色，探索对自指与自生成结构的定性认识和定量刻画方法，探索对生命及类生命的活系统复杂性的全新认识。

读书会详情：自生成结构读书会启动：剖解生命、意识与智能的核心结构

4. 第三次转型：我们已经超越了牛顿范式

这些事实意味着，无论我们感到惊讶与否，我们都处在科学的第三次重大转型当中了。如果我们既不能编写出也不能解出生物圈中历时演化的微分方程，那么我们就已经超出了牛顿范式所涵盖的范畴。新兴的生物宇宙学领域的最新研究也得出了同样的结论：演化的生物圈已超越了牛顿范式[17,19]。

不断演化的生物圈会进入它创造的相邻的可能性，然而我们却无法推导出相邻可能性中的“存在”是什么。我们无法获得这个过程的样本空间，因此既不能定义概率测度，也不能定义“随机”。我们无法进行充分的预测。这与常见的 Kolmogorov 概率公理形成了鲜明对比[41]，Kolmogorov 概率公理的样本空间必须是已知的。

以上这些结论的意义非常重大。如果我们不能为我们的生物圈，或任何生物圈的历时演化编写和求解方程，并且我们不断演变的宇宙中至少有一个不断演变的生物圈，那么就不可能有一个涵盖演化宇宙中存在的所有事物的“万物理论”（theory of everything）。

这个结果一开始可能有点意外，但也许并不完全令人惊讶。哥德尔的第一不完备性定理保证，任何像算术这样，充分拥有有一致公理的系统都具有这样的性质：在给定公理和推理规则的情况下，至少存在一个命题，这个命题无法在系统内被证明或证伪。这个不可证明的命题本身是以算法方式生成的。如果将这个以算法方式生成的命题本身添加到初始公理中，则新的公理集合会再次以算法方式生成真值无法被证明或证伪的命题。

生物圈的演化不仅给出了哥德尔定理的实例，而且还远远超过了它。新的适应性，如分子的新用途，就像引擎块的新用途一样，不能从旧用途中推导出来。重要的是，可供性是参考自由度（referential degrees of freedom），而不是世界独立的物理特征。因此，在新的适应之前，可参照的新用途不能作为一个定理从现有分子的性质和功能，以及生物体的其他物理性质的知识中推导出来[15]。因此，它们不仅仅是类似于仅由算法生成的并无决定性的语句的类比。它们可以被解读为：如果我在生物圈中以一种新的方式存在一段时间。我的新存在，甚至我存在的可能性，都不能从截至目前为止的生物圈中推导出来。

最近的研究结果进一步证实了我们的说法。这些结果表明，宇宙中没有任何建模者能够构建一个完整的宇宙模型[45]。再强调一次，不可能存在“万物理论”。

不管是否情愿，我们观察到了我们或任何生物圈的演化都处在牛顿范式之外。那么这都有哪些影响呢？

1. 真的没有一个“万物理论”可以涵盖在不断演化的宇宙中出现的所有事物。这种万物理论的梦想是壮丽的，是很多杰出的科学家数个世纪的驱动力。希望我们的观点是错误的，如果是这样的话，请击败它们吧。

2.我们或宇宙中任何生物圈的演化不仅不被任何法则所涵盖，甚至似乎无法通过已知技术进行数学计算。但也许我们还可以发明新的数学来描述它。

3.如果没有任何法则可以规定生物圈的演化，而这种演化甚至无法进行数学化描述，那么生物演化就是彻底“自由的”，并且具有极大的创造性。下面的第5节希望找到能产生这种持续创造的一些意想不到的原因。

4.最重要的是，我们确实处于科学的第三次转型中。如果海森堡的不确定关系要求超越经典物理学的转型，我们无法使用集合论推导生物圈的演化似乎预示着另一个重大转型。这种转型的规模和意义目前还不太清楚。我们的宇宙以我们未知的方式展现其创造力。而我们对世界的理解将会因此改变。

我们的概念演示在图1中进行了说明。

图1 展示了我们论证的主要元素和关系的概念性示意图。W_t表示t时刻的‘世界’；经过时间间隔τ后，世界会发生变化。生物演化带来新的达尔文预适应和新的相关变量。生物体是康德式整体，其部分为了整体，并经由整体而存在于寰宇间。自然选择是一种‘向下的因果关系’。解释性箭头指向上方。存在的东西不能从下面的基础推导出来。还原论（reductionist）失败。选择作用于康德式整体，并在其部分演化出新的适应性，以更好地维持康德式整体并繁衍其部分。我们无法使用基于集合论的数学来推导出这些新的适应特征。因此，不存在基于集合论或更广泛地从t时刻的生物世界到t+τ时刻的生物世界的数学映射。因此，从时刻t+τ的世界模型来预测实际世界的映射μ的可能性不存在。我们既不能推导出生物圈的演化，也不能估计我们预测的误差。

5. 综合功能的演变：涌现不是工程

如果生命的演化无法被推导出来，而我们必须放弃我们钟爱的牛顿范式。那么一个广阔的，未知的世界就会展现在我们眼前。

我们对演化生物圈中，几乎奇迹般的自我建构和自发的协调功能组织获得了新的认识：在任何物理事物的不同用途之间不存在推导关系，比如在细胞中可以演化出用于催化反应的蛋白质不能推导出其后续会演化出承载张力负载或者托举分子马达的蛋白质。此外，细胞在物理上构建自己，并通过可遗传的变异和自然选择进化，不断获得不可推导的新可供性。

因此，生物圈中的细胞和有机体中的每个分子和结构都可以被单独使用，或与其他事物一起协同使用。为了无限的适应性新用途而被合并选择（co-opted）和选择，从而不断出现无数的新适应和新的物理事物，如新的蛋白质。这些新的用途不能从旧的用途推导出来。

然而，神奇的是，尽管一直在持续转变，这个整体的整合功能却总是被保持得很好，因为各部分的功能演化必须始终被整合到维持功能性的整体中，这是选择所作用的康德式整体的性质。

选择作用于整体，决定了在非遍历的生物圈中，一段时间内“存在”的是什么。这是“向下的因果关系”。解释性箭头不仅指向下方[46]。

生物圈的演化确实是一个繁殖适应性构建（propagating adapting construction）过程，而不是演绎过程。这是在不断发展的康德式整体中进行的“持续功能整合的涌现”（sustained functional integrated emergence）。并带来了越来越高的适应度。

这就是涌现（emergence）。涌现不是工程。这种共同演化的生物圈的出现本身就是超越了牛顿范式。我们正处于科学的第三次转型，超越牛顿的伟大范式，这并不是一种损失，相反，这是一种邀请，让我们参与这种我们以前从未见过的神奇涌现。

我们开始很难理解这一点。一个不断演化的生物圈是一个自我构建、功能整合的开花涌现绽放过程。这种新的理解与佛教的“因缘起”的古老概念有着共通之处[47]。

一个不断演化的生物圈是一种不断繁殖的构造，而不是必然的演绎的过程。

不断发展的生物圈是不断涌现和创新的。土壤中共同演化的真菌和细菌创造了不断变化的“可能性气泡”，改变了生物圈的相空间。科学的第三次转变需要新的工具、实验和观测，以了解不断演变的生物圈和全球经济如何持续创造无法推导的新可能性。

科学的第三次转型的核心含义是，我们无法“指挥和控制”共同演化的生物圈。隐藏在我们写的方程式后面，我们看不到生命演化的奥秘所隐藏的现实。我们是演化的一部分，而非凌驾于其上的造物。

6. 结论

如预期，21世纪正在成为生物学的世纪。这当然包括生物技术的爆炸、21世纪医学的出现以及对现有细胞和生物体在分子、细胞、有机体和生态系统水平上作为物理系统“运作”（work）的更深入分析。在这里，对物理学、化学、生物物理学、生物化学和分子生物学的依赖是必不可少的。这些问题既复杂又重要。我们正处于系统生物学时代。

然而，继牛顿力学和量子力学两次转型之后，我们面临着科学的第三次重大转型。我们被迫走出美妙的牛顿范式。我们要接受，真的没有“万物理论”：我们或任何生物圈的历时演化都超越了推演法则，超越了基于集合论的数学。

宇宙中可能有10¹⁹个生物圈。演化中的生物圈具有极大的创造性，乃至超出了我们所知，也超出了我们的表述能力。面对神秘，我们选择向前。这意味着我们人类是自然界的一部分，而不是凌驾于自然之上。与其说是损失，不如说是一个巨大的邀请。我们可以尝试用新的方式理解生物圈，理解全球经济，甚至理解我们的文化是如何在数十亿、数百万和几十万年的时间里，通过不可推导、不必然、不断创新、不遍历的涌现，历时性地构建自己。我们不可避免地被邀请去重新看待现实。我们不可避免地被邀请负起责任、尊重并惊叹地分享共同创造生物圈不断演化的现实。

参考文献

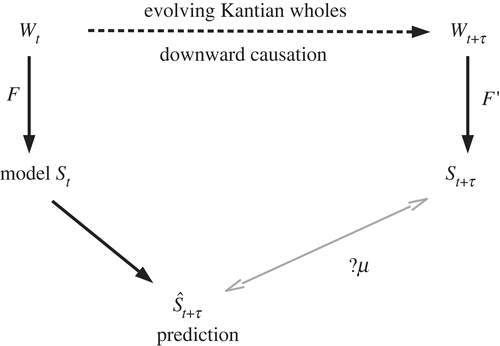
Anderson PW. 1972More is different: broken symmetry and the nature of the hierarchical structure of science. Science 177, 393-396. (doi:10.1126/science.177.4047.393) Crossref, PubMed, ISI, Google Scholar
Nature Physics. 2022Complexity matters (editorial). Nat. Phys. 18, 843. (doi:10.1038/s41567-022-01734-5) Crossref, Google Scholar
Smolin L. 2013Time reborn: from the crisis in physics to the future of the universe. London, UK: Penguin Books. Google Scholar
Planck M. 1901On the law of distribution of energy in the normal spectrum. Ann. Phys. 4, 1. Google Scholar
Heisenberg W. 1927Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik/The physical content of quantum kinematics and mechanics. Z. Phys. 43, 172-198. Translation published in [6]. (doi:10.1007/BF01397280) Crossref, Google Scholar
Wheeler JA, Zurek WH. 2014Quantum theory and measurement. Princeton, NJ: Princeton University Press. Google Scholar
Heisenberg W. 1958Physics and philosophy: the revolution in modern science. New York, NY: Harper. Google Scholar
Feynman RP. 1998Quantum electrodynamics. Boulder, CO: Westview Press. Google Scholar
Birkhoff G, Von Neumann J. 1936The logic of quantum mechanics. Ann. Math. 37, 823-843. (doi:10.2307/1968621) Crossref, Google Scholar
Svirezhev YM. 2008Nonlinearities in mathematical ecology: phenomena and models: would we live in Volterra’s world?Ecol. Modell. 216, 89-101. (doi:10.1016/j.ecolmodel.2008.03.028) Crossref, Google Scholar
Longo G, Montévil M, Kauffman SA. 2012No entailing laws, but enablement in the evolution of the biosphere. In Proc. of GECCO 2012—the 14th Genetic and Evolutionary Computation Conf., July 7–11, 2012, in Philadelphia, USA, pp. 1379–1392. New York, NY, USA: ACM. Google Scholar
Montévil M, Mossio M. 2015Biological organisation as closure of constraints. J. Theor. Biol. 372, 179-191. (doi:10.1016/j.jtbi.2015.02.029) Crossref, PubMed, ISI, Google Scholar
Kauffman SA. 2019A world beyond physics: the emergence and evolution of life. New York, NY: Oxford University Press. Google Scholar
Kauffman SA. 2020Answering Schrödinger’s ‘what is life?’. Entropy 22, 815. (doi:10.3390/e22080815) Crossref, PubMed, ISI, Google Scholar
Kauffman SA, Roli A. 2021The world is not a theorem. Entropy 23, 1467. (doi:10.3390/e23111467) Crossref, PubMed, Google Scholar
Kauffman SA, Jelenfi DP, Vattay G. 2020Theory of chemical evolution of molecule compositions in the universe, in the Miller–Urey experiment and the mass distribution of interstellar and intergalactic molecules. J. Theor. Biol. 486, 110097. (doi:10.1016/j.jtbi.2019.110097) Crossref, PubMed, Google Scholar
Cortês M, Kauffman SA, Liddle AR, Smolin L. 2022Biocosmology: biology from a cosmological perspective. arXiv 2204.09379. (https://arxiv.org/abs/2204.09379) Google Scholar
Ashkenasy G, Jagasia R, Yadav M, Ghadiri MR. 2004Design of a directed molecular network. Proc. Natl Acad. Sci. USA 101, 10 872-10 877. (doi:10.1073/pnas.0402674101) Crossref, ISI, Google Scholar
Cortês M, Kauffman SA, Liddle AR, Smolin L. 2022Biocosmology: towards the birth of a new science. arXiv 2204.09378. (https://arxiv.org/abs/2204.09378) Google Scholar
Atkins PW. 1984The second law. New York, NY: Scientific American Library. Google Scholar
Gibson JJ. 1966The senses considered as perceptual systems. Boston, MA: Houghton Mifflin. Google Scholar
Walsh DM. 2015Organisms, agency, and evolution. Cambridge, UK: Cambridge University Press. Crossref, Google Scholar
Gould SJ, Vrba ES. 1982Exaptation—a missing term in the science of form. Paleobiology 8, 4-15. (doi:10.1017/S0094837300004310) Crossref, ISI, Google Scholar
Prum RO, Brush AH. 2002The evolutionary origin and diversification of feathers. Q. Rev. Biol. 77, 261-295. (doi:10.1086/341993) Crossref, PubMed, ISI, Google Scholar
Persons IV WS, Currie PJ. 2015Bristles before down: a new perspective on the functional origin of feathers. Evolution 69, 857-862. (doi:10.1111/evo.12634) Crossref, PubMed, Google Scholar
Barve A, Wagner A. 2013A latent capacity for evolutionary innovation through exaptation in metabolic systems. Nature 500, 203-206. (doi:10.1038/nature12301) Crossref, PubMed, ISI, Google Scholar
Kauffman SA. 2016Humanity in a creative universe. New York, NY: Oxford University Press. Google Scholar
Jech T. 2006Set theory. New York, NY: Springer. Google Scholar
Moore GH. 2012Zermelo’s axiom of choice: its origins, development, and influence. North Chelmsford, MA: Courier Corporation. Google Scholar
Potter M. 2004Set theory and its philosophy: a critical introduction. Oxford, UK: Clarendon Press. Crossref, Google Scholar
Russell B, Whitehead A. 1973Principia mathematica. Cambridge, UK: Cambridge University Press. Google Scholar
Peano G. 1889Arithmetices principia: nova methodo exposita. Milan, Italy: Fratres Bocca. Google Scholar
Grabiner JV. 1983Who gave you the epsilon? Cauchy and the origins of rigorous calculus. Am. Math. Mon. 90, 185-194. (doi:10.1080/00029890.1983.11971185) Crossref, ISI, Google Scholar
Robinson A. 2016Non-standard analysis. Princeton, NJ: Princeton University Press. Google Scholar
Roli A, Jaeger J, Kauffman SA. 2022How organisms come to know the world: fundamental limits on artificial general intelligence. Front. Ecol. Evol. 9, 1035. (doi:10.3389/fevo.2021.806283) Crossref, Google Scholar
Kauffman SA, Roli A. 2022What is consciousness? Artificial intelligence, real intelligence, quantum mind and qualia. Biol. J. Linn. Soc.Blac092. (doi:10.1093/biolinnean/blac092) Crossref, Google Scholar
von Neumann J. 1955Mathematical foundations of quantum mechanics. Princeton, NJ: Princeton University Press. Google Scholar
Wigner EP. 1995Remarks on the mind-body question. In Philosophical reflections and syntheses: the collected works of Eugene Paul Wigner (Part B, Historical, philosophical, and socio-political papers) (ed. J Mehra), pp. 171-184. Berlin, Germany: Springer. Google Scholar
Shimony A. 1997On mentality, quantum mechanics and the actualization of potentialities. In The large, the small and the human mind (ed. Penrose R), pp. 144-160. Cambridge, UK: Cambridge University Press. Google Scholar
Svetlichny G. 2011Qualia are quantum leaps. arXiv 1104.2634. (https://arxiv.org/abs/1104.2634) Google Scholar
Kolmogorov A. 2018Foundations of the theory of probability. Mineola, NY: Courier Dover Publications. Google Scholar
Kaku M. 2021The god equation: the quest for a theory of everything. New York, NY: Doubleday. Google Scholar
Franzén T. 2005Gödel’s theorem: an incomplete guide to its use and abuse. Boca Raton, FL: CRC Press. Google Scholar
Longo G. 2019Interfaces of incompleteness. In Systemics of incompleteness and quasi-systems (eds G Minati, M Abram, E Pessa), pp. 3–55. New York, NY: Springer. Google Scholar
Devereaux A, Koppl R, Kauffman SA, Roli A. 2021Constraints on modeling systems from within systems: the principle of frame relativity. SSRN. (doi:10.2139/ssrn.3968077) Google Scholar
Weinberg S. 1994Dreams of a final theory. New York, NY: Vintage. Crossref, Google Scholar
Laumakis SJ. 2008Interdependent arising. In Cambridge introductions to philosophy, pp. 105-124. Cambridge, UK: Cambridge University Press. Google Scholar

（参考文献可上下滑动查看）

因果涌现系列读书会

跨尺度、跨层次的涌现是复杂系统研究的关键问题，生命起源和意识起源这两座仰之弥高的大山是其代表。因果涌现理论、机器学习重整化技术、信息论或信息分解等近年来新兴的理论与工具，有望破解复杂系统的涌现规律。

集智俱乐部因果涌现读书会目前已经进行了四季。第一季读书会系统地梳理了因果涌现的概念，以及它与Sloopy Model、复杂性阈值、自指等概念之间的联系，也探讨了因果涌现理论在复杂网络、机器学习中的应用。参看：因果涌现读书会启动：连接因果、涌现与自指——跨尺度动力学与因果规律的探索。

第二季读书会探讨了涌现、因果科学和机器学习三大主题的融合，包括信息论拓展、因果涌现理论、因果表示学习、多尺度机器学习动力学建模。参看：因果、涌现与机器学习：因果涌现读书会第二季启动。

第三季读书会进一步围绕因果涌现的核心问题「因果涌现的定义」以及「因果涌现的辨识」进行深入学习和讨论，对 Erik Hoel 提出的 Causal Emergence，Causal Geometry 等因果涌现的核心理论进行探讨和剖析，并详细梳理其中涉及到的方法论，包括从动力学约简、隐空间动力学学习等其他领域中学习和借鉴相关的研究思路，最后探讨因果涌现的应用，包括基于生物网络、脑网络或者涌现探测等问题展开扩展，发掘更多的实际应用场景。参看：因果涌现读书会第三季启动：深入多尺度复杂系统核心，探索因果涌现理论应用

正在进行的第四季读书会主题是「新信息论：从分解到整合」，重点梳理信息分解与整合信息论的相关研究。参看：新信息论：从分解到整合｜因果涌现读书会第四季启动

因果涌现社区聚集了600+成员，积累了大量论文解读资料。欢迎感兴趣的朋友报名，加入因果涌现社区，解锁对应录播权限。