伊辛模型和自旋玻璃等经典多体系统在统计物理的发展中起到了重要作用,特别是对相变和临界现象的理解。这类系统面临的一个核心问题是计算配分函数。简而言之,平衡态统计力学告诉我们,当系统处于热平衡时,某个构型s出现的概率遵循玻尔兹曼分布 p(s)=e–βE(s)/Z,其中E(s)是能量函数, β是逆温度。这个概率表达式里出现了一个难以计算的分母Z,也称配分函数:假设每个自旋有d种可能的取值,系统总共有N个自旋,那么配分函数Z=∑se–βE(s)的计算需要对所有dN种可能构型的e–βE(s)进行求和。这在计算复杂性理论中属于#-P难问题。配分函数之所以重要,不仅因为它是沟通微观构型与宏观物理量的桥梁,而且如果想精确计算某一个构型出现的概率p(s),或是从p(s)中采样,都需要处理分母中出现的配分函数。这一困难也广泛地存在于概率图模型等机器学习问题中,例如,在变分推断(variational inference)里,后验概率的表达式里同样出现了难以计算的分母。
2019年,中国科学院理论物理研究所的张潘研究员与合作者提出了一种名为变分自回归网络(Variational Autoregressive Networks,简称VAN)的方法,将机器学习中的生成模型方法引入平衡态统计物理的研究领域。如今,生成模型已经变得十分常见且广为人知:生成式人工智能如AI绘画和大语言模型(large language model)等背后的核心就是一类被称为生成模型的机器学习技术。我们用q(s; θ)表示生成模型所参数化的分布。在机器学习任务中,我们的目标是让q(s; θ)能够拟合数据集(例如图像或者文本)所表示的经验分布;而在平衡态统计力学问题的背景下,我们的目标是让q(s; θ)和玻尔兹曼分布p(s)尽可能接近。这一套算法的具体细节可以参看文献[1]。
[1] D. Wu, L. Wang, and P. Zhang, Solving Statistical Mechanics Using Variational Autoregressive Networks, Phys. Rev. Lett. 122, 080602 (2019).
与传统的消息传递和MCMC等方法相比,VAN这一套方法带来了两个重要优势。首先是采样的优势:类似于大型语言模型,借助GPU等硬件,自回归模型可以帮助我们以无偏且并行的方式生成大量样本:
二是变分原理保证了VAN方法计算得到的自由能是真实自由能的上界:
这意味着VAN方法得到的自由能估计值不会低于真实自由能的值。
VAN方法在平衡态统计物理中展示了巨大的应用潜力,并引起了广泛关注。随后,大量相关的后续工作涌现出来。到了2023年,张潘课题组与汤迎课题组合作,首次将VAN方法的应用扩展到非平衡态领域[2]。
[2] Y. Tang, J. Weng, and P. Zhang, Neural-Network Solutions to Stochastic Reaction Networks, Nature Machine Intelligence 5, 376 (2023).
在这里,平衡态指系统的状态与时间无关,而非平衡态意味着系统的状态会随时间发生变化。对于非平衡态系统,其状态可以用一组随时间变化的函数描述,其演化过程受系统背后的物理定律支配,通常可以表示为微分方程的形式。在这项研究中,汤迎等关注的是一类称为随机反应网络的问题,它被广泛用于模拟物理、化学和生物学中的随机过程。随机反应网络可以使用化学主方程来建模,描述了物种分子数的联合概率p(n, t)随时间的演化:
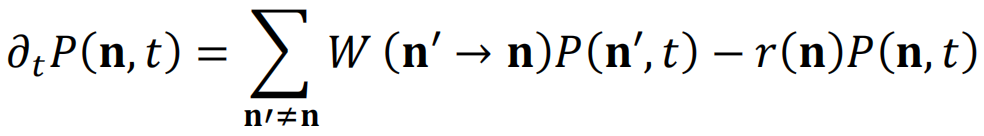
与Gillespie算法等随机模拟算法不同,汤迎等所发展的方法直接使用VAN来描述联合概率分布随时间的演化。由于主方程的形式由动力学给定且已知,因此可以计算出在当前状态下演化一个极小时间步后的新分布,并重新训练一个新的生成模型。这样就实现了一个极小时间步的演化。
在最近发表的论文《Learning nonequilibrium statistical mechanics and dynamical phase transitions》中,我们专注于一类称为运动约束模型(kinetically constrained model)的非平衡态系统[3]。这种模型与伊辛模型一样,设计简单且广泛应用于玻璃态系统的动力学建模。我们以最简单的一维FA模型为例,每个格点上包含一个二值变量xi={0, 1},xi=1表示该格点被粒子占据,xi=0表示该格点未被粒子占据。模型中的转移速率由下面表达式给出:
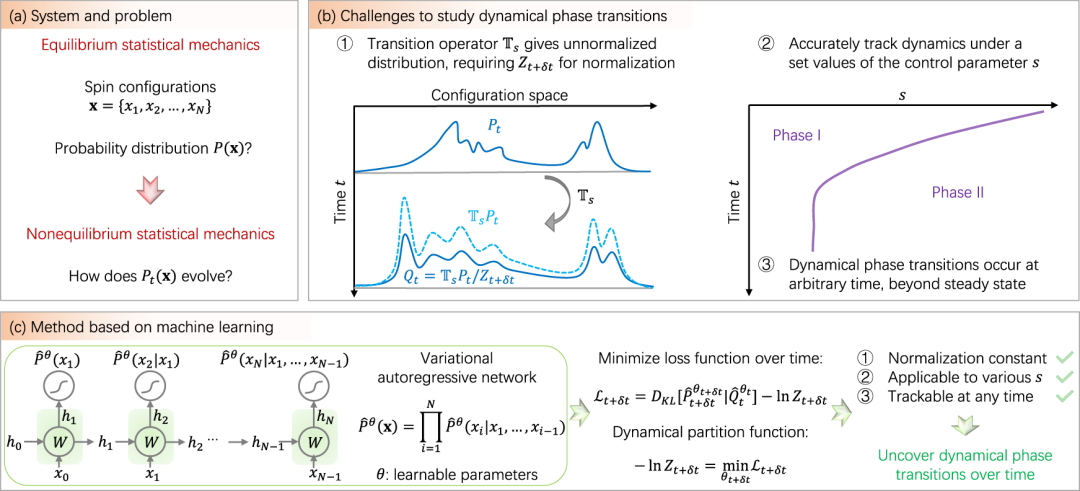
其中c是系统平衡时的粒子平均占据数,(xi-1+xi+1)表示运动约束(kinetic constraint)。当不存在运动约束时,该模型变为一个简单的单自旋翻转的Glauber动力学;当存在运动约束时,动力学仍然满足细致平衡条件,理论上经过足够长的时间,系统将演化到平衡态,即每个粒子平均占据数为c。然而,运动约束对动力学过程产生了非平凡的影响。当c→0.5时,运动约束的效果并不显著,此时系统中接近一半的格点都被占据,因此动力学可以持续进行。然而在c<<1的情况下,运动约束的效果开始显现。一方面,系统演化到平衡态意味着极小的粒子占据数;另一方面,动力学本身却需要足够多的被占据粒子数来驱动。这种平衡态和动力学之间的相互竞争使得系统需要经过非常长的时间才能达到最终的平衡态。因此,运动约束模型能够建模玻璃的结构弛豫(structure relaxation)等现象。下图我们给出了平衡态Ising模型和非平衡态运动约束模型相关概念的一个对比。
图1:通过演化变分自回归网络,借助强化学习算法追踪系统演化到任意时刻状态的联合概率分布。
通过类比平衡态统计物理的系综和配分函数等概念,运动约束模型这类非平衡系统的核心任务是计算动力配分函数(dynamical partition function):
和前面介绍的平衡态情况下的配分函数相比,动力配分函数的计算不仅需要对所有可能的状态求和,还需要考虑额外的时间维度,因此其计算难度远大于平衡态中的配分函数。如果我们只关注系统在长时间演化后的情况,那么大偏差(large deviation)理论可以帮助我们将这个含时的动力配分函数计算问题转化为不含时的最大特征值计算问题。然而,计算系统在任意有限时间下的动力配分函数仍然是一个棘手的问题,因为这要求我们追踪系统在每个时刻的状态概率分布P(x, t)。
借助演化VAN的思想,我们提出的算法能够精确计算二维及三维模型的动力配分函数。简单来说,对于这类服从马尔可夫动力学的非平衡态系统,系统在t时刻处于某个状态x的概率P(x, t)服从主方程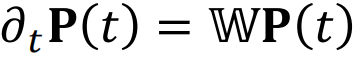 ,其中P(t)表示所有可能的状态向量(P(x1, t),…,P(xM, t)),
,其中P(t)表示所有可能的状态向量(P(x1, t),…,P(xM, t)), 取决于系统的转移速率。我们提出使用VAN参数化系统在某个时刻t下状态的概率分布Pθ(x, t)。之后,通过最小化损失函数
取决于系统的转移速率。我们提出使用VAN参数化系统在某个时刻t下状态的概率分布Pθ(x, t)。之后,通过最小化损失函数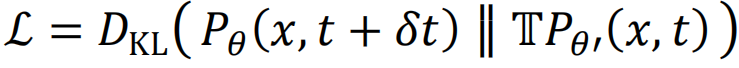 ,其中
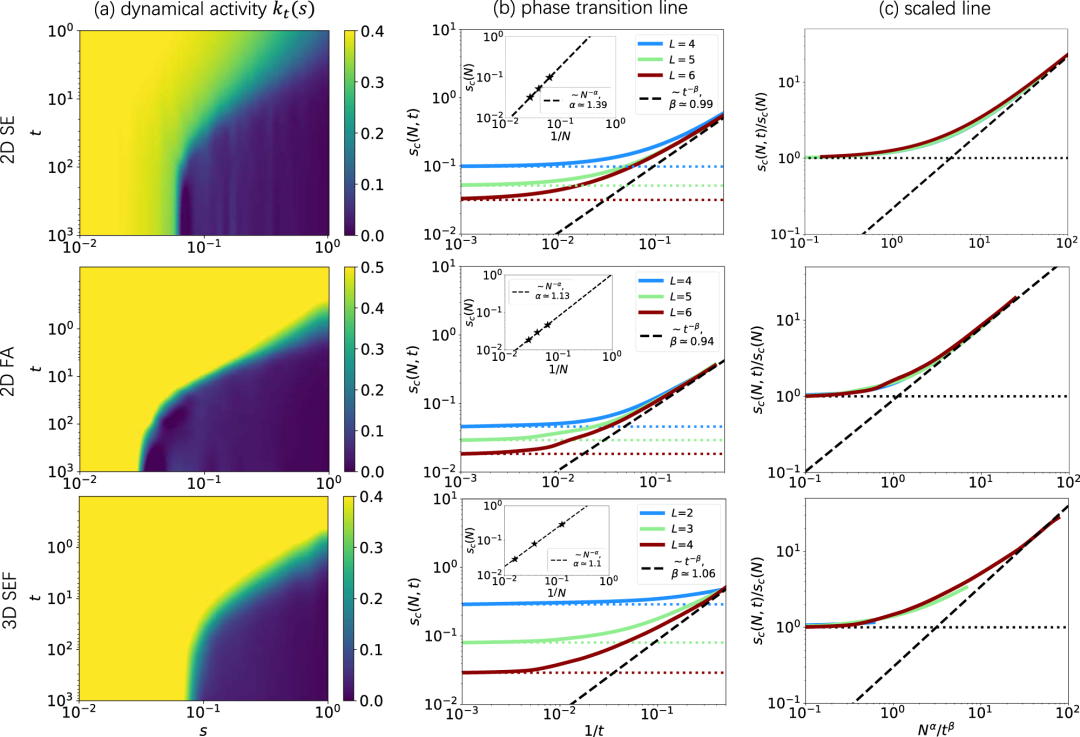
,其中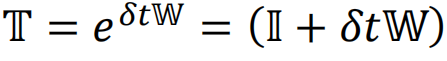 表示演化δt时间的演化算符,便能够学习系统在t+δt时刻的概率分布。这一算法不仅成功揭示了运动约束模型这类非平衡态系统独有的动力学相变现象,而且通过有限尺度标度分析,首次为二维和三维系统的临界指数提供了准确的估计。
表示演化δt时间的演化算符,便能够学习系统在t+δt时刻的概率分布。这一算法不仅成功揭示了运动约束模型这类非平衡态系统独有的动力学相变现象,而且通过有限尺度标度分析,首次为二维和三维系统的临界指数提供了准确的估计。
图2:借助基于变分自回归网络的有限时间演化算法,成功揭示了二维及三维运动约束模型的动力学相变现象,并计算得到了相关临界指数。
鉴于生成模型的通用性,演化VAN方法不仅适用于随机反应网络和运动约束模型,还可以应用于其他类型和任意拓扑结构的马尔科夫动力学系统。例如,我们可以使用基于图神经网络架构的演化VAN来研究图上的投票者模型和网络上的流行病传播模型。此外,这套方法还可以推广到量子物理中具有不同维度动力学约束的模型,并结合Doob算子、主动学习和强化学习来采样稀有轨迹。另外一个值得探索的问题是,大型语言模型是否能够帮助我们更有效地处理更一般的非平衡态系统的演化问题。
参考文献
[1] D. Wu, L. Wang, and P. Zhang, Solving Statistical Mechanics Using Variational Autoregressive Networks, Phys. Rev. Lett. 122, 080602 (2019).
[2] Y. Tang, J. Weng, and P. Zhang, Neural-Network Solutions to Stochastic Reaction Networks, Nature Machine Intelligence 5, 376 (2023).
[3] Y. Tang, J. Liu, J. Zhang, and P. Zhang, Learning Nonequilibrium Statistical Mechanics and Dynamical Phase Transitions, Nature Communications 15, 1117 (2024).
刘晶,中国科学院理论物理研究所博士后,博士毕业于北京师范大学系统科学学院,研究方向为生成模型和统计物理的交叉领域。
https://pattern.swarma.org/user/14/master
AI+Science 是近年兴起的将人工智能和科学相结合的一种趋势。一方面是 AI for Science,机器学习和其他 AI 技术可以用来解决科学研究中的问题,从预测天气和蛋白质结构,到模拟星系碰撞、设计优化核聚变反应堆,甚至像科学家一样进行科学发现,被称为科学发现的“第五范式”。另一方面是 Science for AI,科学尤其是物理学中的规律和思想启发机器学习理论,为人工智能的发展提供全新的视角和方法。
集智俱乐部联合斯坦福大学计算机科学系博士后研究员吴泰霖(Jure Leskovec 教授指导)、哈佛量子计划研究员扈鸿业、麻省理工学院物理系博士生刘子鸣(Max Tegmark 教授指导),共同发起以“AI+Science”为主题的读书会,探讨该领域的重要问题,共学共研相关文献。读书会已完结,现在报名可加入社群并解锁回放视频权限。

详情请见:



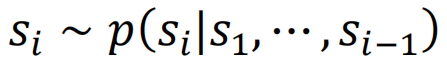
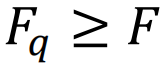
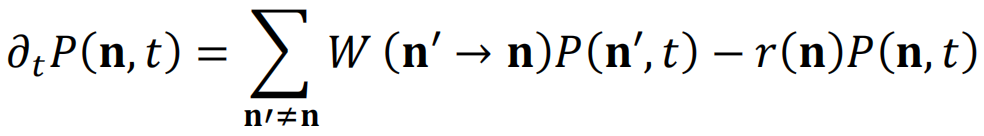
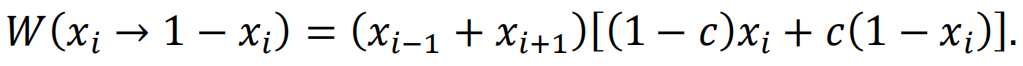

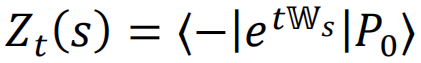
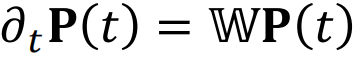 ,其中P(t)表示所有可能的状态向量(P(x1, t),…,P(xM, t)),
,其中P(t)表示所有可能的状态向量(P(x1, t),…,P(xM, t)), 取决于系统的转移速率。我们提出使用VAN参数化系统在某个时刻t下状态的概率分布Pθ(x, t)。之后,通过最小化损失函数
取决于系统的转移速率。我们提出使用VAN参数化系统在某个时刻t下状态的概率分布Pθ(x, t)。之后,通过最小化损失函数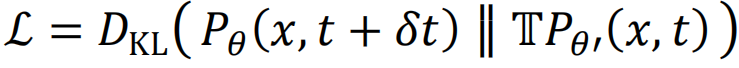 ,其中
,其中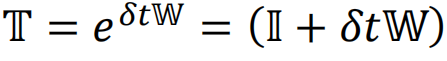 表示演化δt时间的演化算符,便能够学习系统在t+δt时刻的概率分布。这一算法不仅成功揭示了运动约束模型这类非平衡态系统独有的动力学相变现象,而且通过有限尺度标度分析,首次为二维和三维系统的临界指数提供了准确的估计。
表示演化δt时间的演化算符,便能够学习系统在t+δt时刻的概率分布。这一算法不仅成功揭示了运动约束模型这类非平衡态系统独有的动力学相变现象,而且通过有限尺度标度分析,首次为二维和三维系统的临界指数提供了准确的估计。