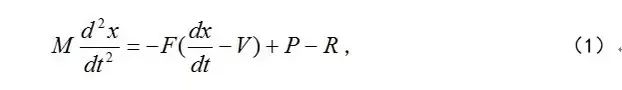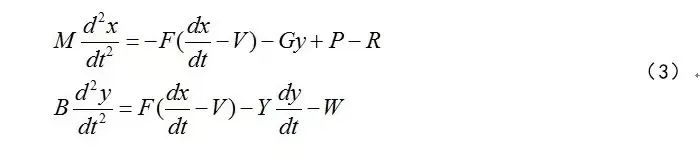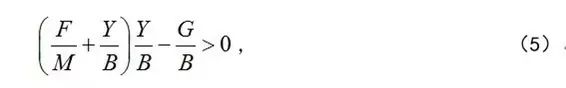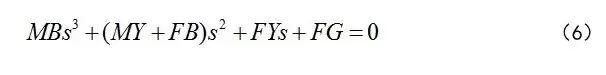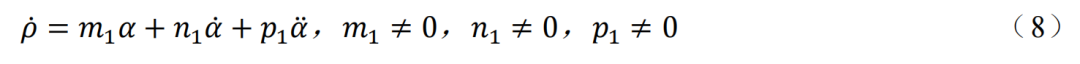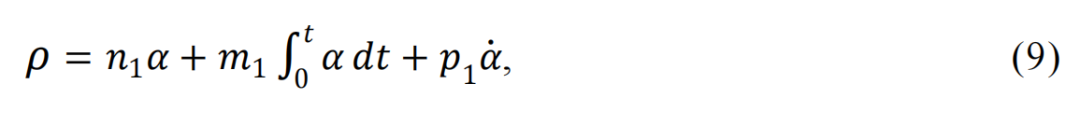图2. 走马观花线路图(2019国科大《控制论》课程)
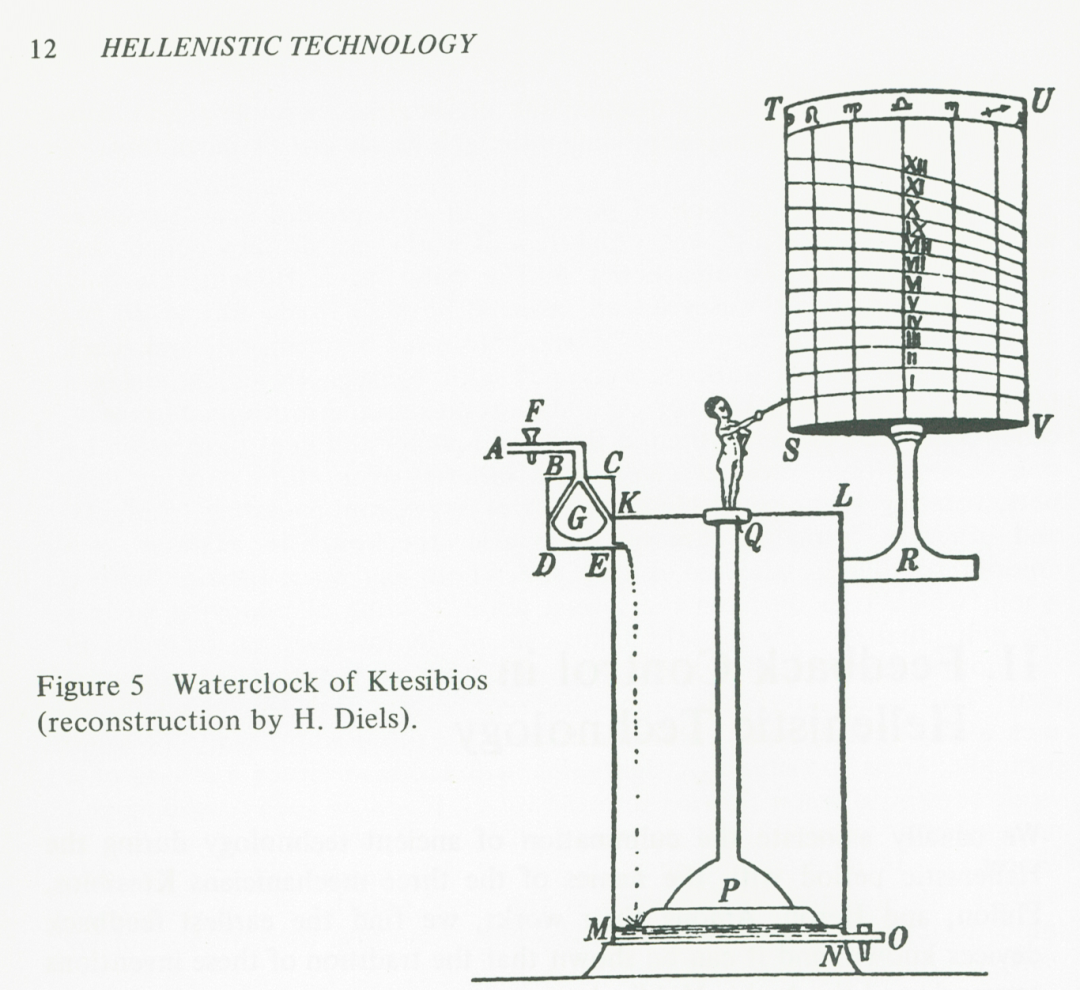
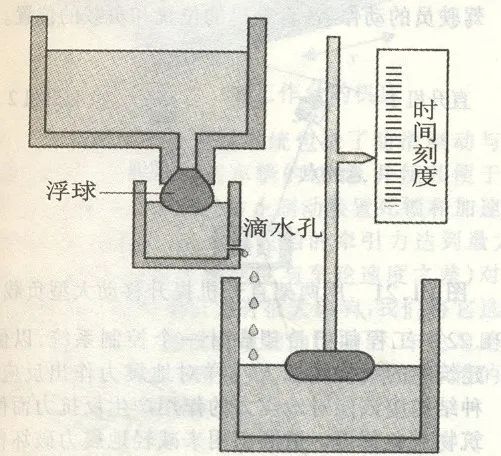
一般认为,最早的控制系统是公元前300年至公元1年古希腊人和阿拉伯人发明的浮球调节装置,如水钟[3,4](见图3、图4)。
图4为水钟中的浮球调节装置示意图[3],水从漏壶中以恒定的流量注入受水壶,浮在受水壶水面上的指针随水面上升指示时间。为了获得恒定的流量,必须使漏壶的水位保持恒定。当漏壶水位下降时,浮球随之下降,水自动注入漏壶,漏壶水位上升到设定高度时,浮球自动堵住入水口,漏壶水位保持在设定高度。
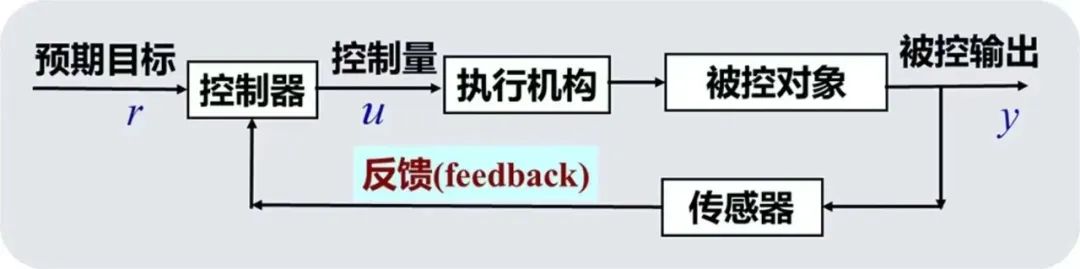
现在我们通常把闭环(反馈)控制系统分为传感器、控制器、执行机构、被控对象等几个基本组成部分(见图5),在浮球调节装置这个设计巧妙的控制系统中,传感器、控制器、执行机构是一体的。
浮球调节装置现在还在我们的日常生活中广泛使用,就是抽水马桶。在我自己学习控制的第一堂课上,老师给我们举的控制系统例子就是抽水马桶,当时还觉得怎么学了个不太“高雅”的专业。
我在课程中一直希望能让学生们将课堂学习与实际联系起来,都会给学生们留一个大作业,每人选取一个自己感兴趣的控制系统结合课程内容进行分析介绍,学生们在这个环节的表现往往一改平时上课的沉闷,一个个熠熠生辉,每每让我心花怒放,惊叹不已。还记得白文艳一开始交上来的选题是“抽水马桶系统”,我给她改了个“好听”一点的题目“浮球液位控制系统”,结果她上台后的开场白是:“老师改的题目有点小了,我今天要讲的是抽水马桶系统中的控制问题”,立刻让我对这个看上去文文静静的小姑娘所表现出的执着的科学精神肃然起敬。
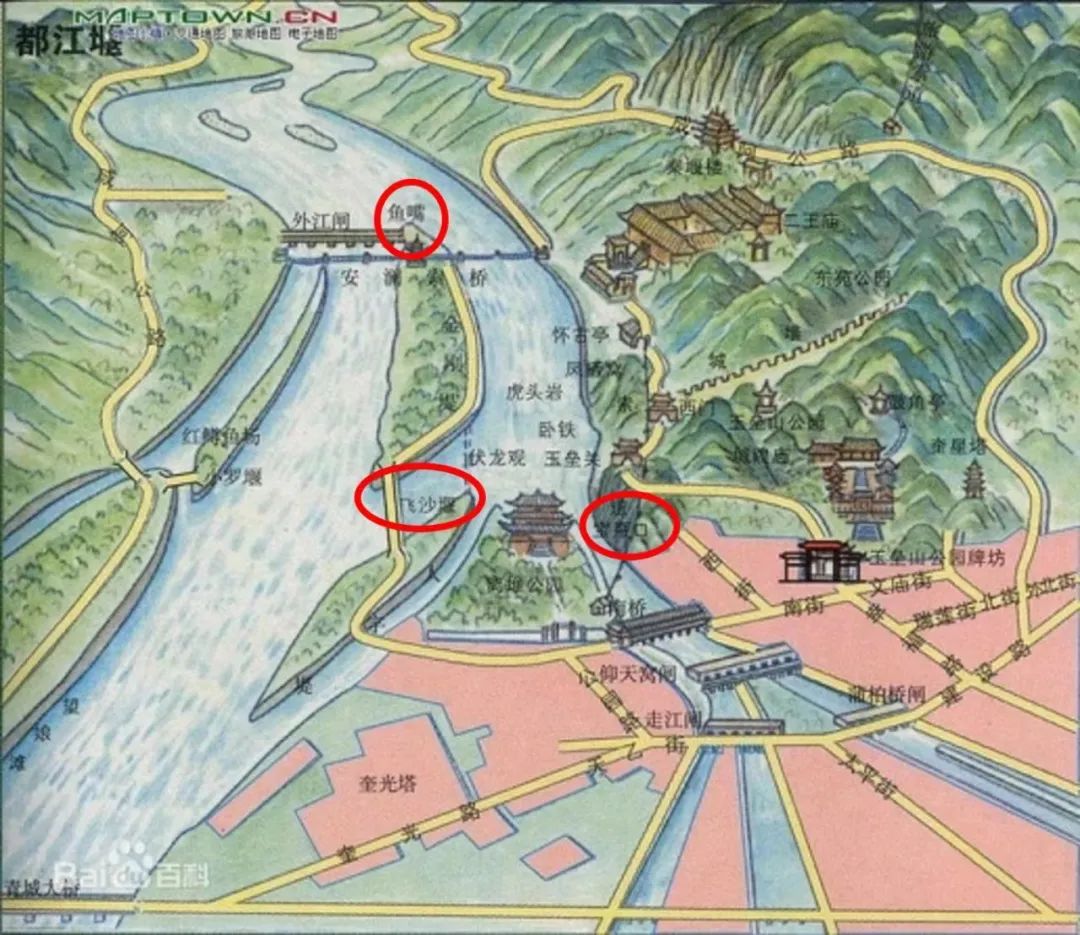
中国古代计时器则有刻漏、水运浑天仪、水运仪象台等(见图6),中国古代著名的控制系统还有指南车、都江堰水利工程等(见图7,图8)。Mayr的书中提到了中国古代的水运仪象台和指南车[4],但对其控制机理还有疑问。都江堰水利工程(约公元前256-前251)则被许多人认为是一个杰出的控制系统,两千多年了,至今依然在造福成都平原。2015年第6届中瑞控制会议在成都召开(见图9),有先到达的瑞典参会人员迫不及待地去了都江堰,回来后就在自己报告的第一页打出都江堰的照片,赞叹这一控制系统。都江堰主体工程包括鱼嘴分水堤、飞沙堰溢洪道和宝瓶口进水口(见图8中三个红圈处),被控量为进入成都的水量,枯水期不能少,丰水期不能多,是个多环节控制系统,而且充满各种扰动、不确定性和时变性。2019年秋季开学前,自抗扰控制群里各位又将开始讲授控制课程的老师们还热烈讨论了一番其控制原理,准备在课上好好讲讲都江堰这个控制系统。
图6. 北宋苏颂、韩公廉等人所制水运仪象台(图片来自网络)
图8. 都江堰水利工程,右上图的三个红圈分别为鱼嘴分水堤、飞沙堰溢洪道和宝瓶口进水口
图9. 2015年3月23-24日第6届中瑞控制会议在成都召开
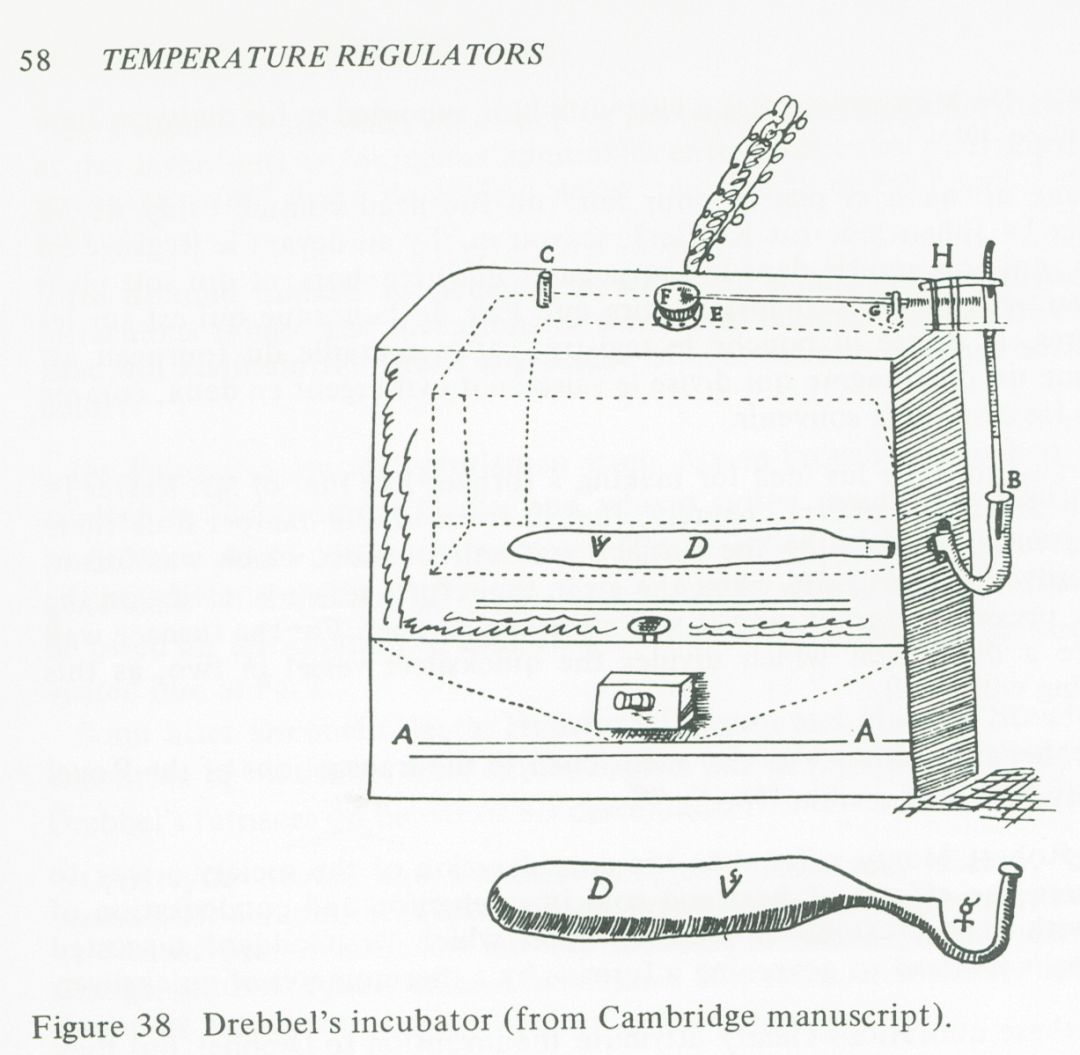
近代欧洲最早发明的反馈控制系统是荷兰人Cornelis Drebbel(1572-1633)发明的培育箱温度调节器(见图10、图11)[3,4,5]。
图10. 荷兰人Drebbel发明的恒温培育箱[4]
Drebbel是荷兰发明家,他发明了一个孵化小鸡的培育箱,通过控制炉温来给培育箱加热。图11为培育箱温度控制装置示意图[5],培育箱是双层的、中间有水,把热量均匀地传递给内层,温度传感器是一个内部装有酒精和水银的容器。当温度过高时,温度传感器的水银柱上升,阀门关闭,减少进气,降低温度;反之则水银柱下降,阀门打开,增加进气,提高温度。
3. 最早应用于工业过程的反馈系统:
瓦特飞球式调速器
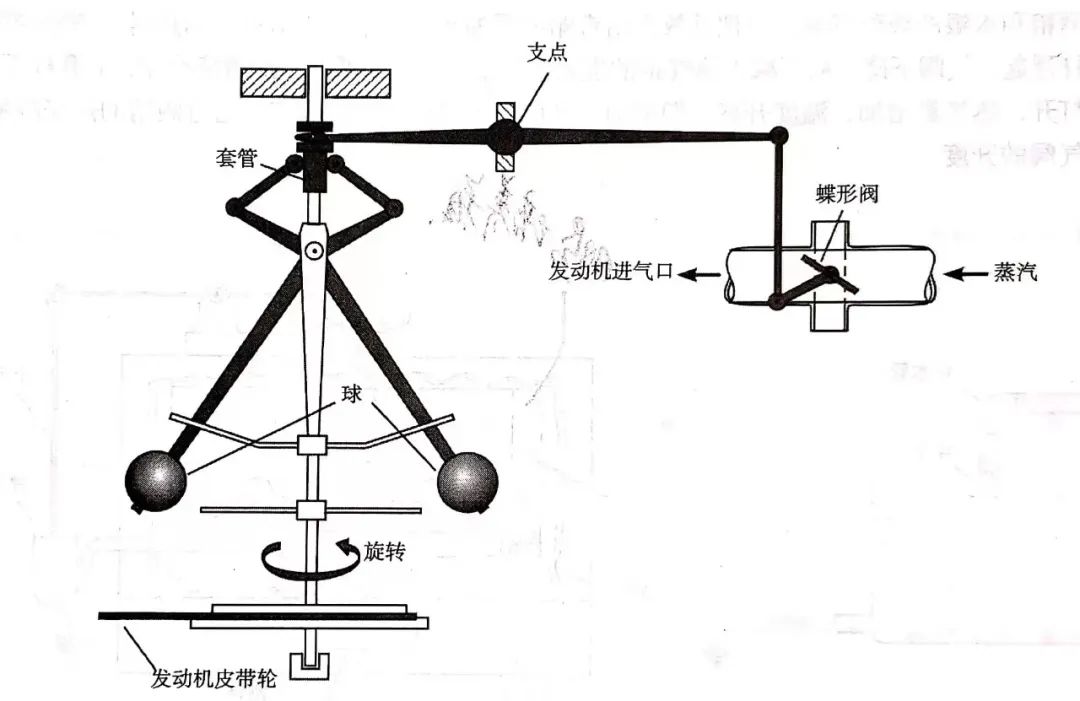
人们普遍认为最早应用于工业过程的控制器是瓦特(James Watt,1736-1819)1788年应用于蒸汽机的飞球式调速器(Fly-ball Governor,见图12)[3]。
图12. 放置在西班牙马德里理工大学的一台1859年制造的瓦特蒸汽机,黄圈中为飞球式调速器[39]
飞球式调速器,也称为离心式调速器(Centrifugal Governor)。图13展示了其工作原理[5]:假定蒸汽机运行在平衡状态,两个重球在与中心轴成某一给定角度的锥面上围绕轴旋转。当蒸汽机负载增大时,它的速度降低,两个重球下跌到更小的锥面上旋转,引起杠杆运动打开蒸汽室主阀(执行机构),从而增加进入的蒸汽量,以恢复降低的速度。因此,球与中心轴的角度是用来传感输出速度的。
飞球式调速器被认为是控制发展史上的一个里程碑,Mayr书的封面就是一个飞球式调速器的图片(见图14),我曾在伦敦街头见到一尊雕塑,以飞球式调速器代表科学(见图15)。
图14. Otto Mayr著:The Origins of Feedback Control
关于飞球式调速器,有个误传流传较广,说是瓦特发明的。飞球式调速器并不是瓦特发明的。关于应用离心力控制速度的研究,科学家惠更斯(Christiaan Huygens,1629-1695)和胡克(Robert Hooke,1635-1703)都曾钻研过这个问题,并设计了利用离心力控制速度的装置[6,7](见图16)。到18世纪,在蒸汽机之前,离心力调速器已经在风车上被大量应用。风车技术人员开发了许多新装置,不过他们大多是工程师而不是科学家,因此除了简略的专利,留下的文献纪录很少[6]。图17中是Thomas Mead在1787年申请的控制风车速度的调速器专利中的一张图[4],可以看到其采用了一个双球的离心力调速器。
图16. 惠更斯和胡克都曾钻研过利用离心力控制速度的问题,并设计了有关装置[6]
图17. 1787年, Thomas Mead申请了一个控制风车速度的调节器专利[4]
然后是瓦特蒸汽机登场,瓦特对蒸汽机的改进始于1763年,当时他在格拉斯哥大学(University of Glasgow)几位教授的帮助下,在大学里开设了一间小修理店。这年,他修理了学校的一台纽科门蒸汽机(Newcomen Steam Engine),但当时蒸汽机的效率很低。此后,瓦特对蒸汽机进行了一系列重大改进:如将冷凝器与汽缸分离、采用连续旋转运动的曲柄传动系统、发明了双向气缸、平行运动连杆机构等[8]。1788年瓦特从其合伙人博尔顿(Matthew Boulton)处了解到已经在风车中采用的飞球调速器,意识到可以改进后用于蒸汽机的转速控制,以保证蒸汽机的平稳运行[1,8],于是发明了采用飞球调速器的蒸汽机。
蒸汽机的出现开辟了人类利用能源的新时代,使人类实现了机器大生产,瓦特的改进贡献巨大。后人为了纪念瓦特这位伟大的发明家,把功率的单位定为“瓦特”。
到1868年,约有75000台瓦特调节器在英国使用[6]。最初的瓦特调节器存在的主要问题是:只能在一个运行条件上实现精确控制,即只能在小(负载变化)范围运行[1]。用现在的话说,就是当负载(外扰)变化较大时,控制存在稳态偏差。
瓦特调速器只采用了比例控制,我们采用如下的一个简化模型描述其工作过程:
其中:P为驱动力矩,R为负载力矩,V为设定转速,实际转速为,M为转动惯量,F为反馈增益系数,t为时间,稳态时的速度为:
可见,当驱动力矩P与负载力矩R不匹配时,系统存在与负载R(未知外扰)有关的稳态偏差。
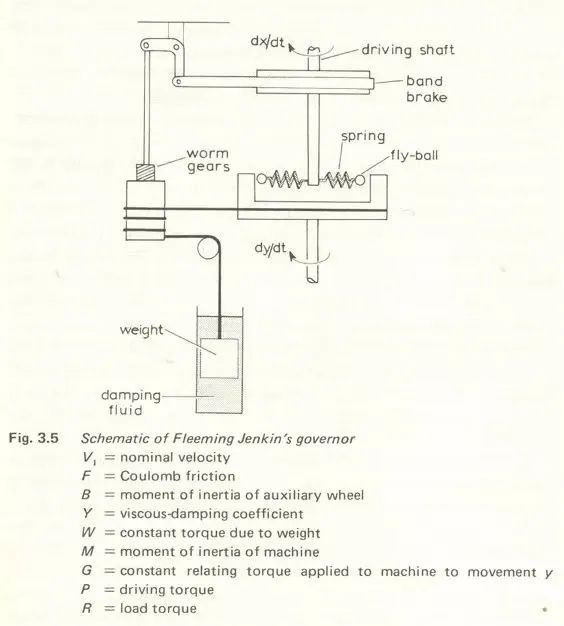
19世纪的前70年,大量的工作围绕改进调速器展开,很多科学家需要采用性能更好的调速器来开展各自领域的研究工作,世界各地出现了大量调速器方面的专利。比如图18所示Fleeming Jenkin设计的调速器[7],在这个设计中,系统平衡点不再受负载外扰R的影响,但却遇到了稳定性问题。19世纪早期出现了关于调速器“hunting(来回摆动,即不稳定)”行为的报告,人们开始努力分析调速器动态特性,寻找稳定(non-hunting)的条件[1]。
图18. Fleeming Jenkin设计的调速器[7]
瓦特是企业家,并没有从事调速器的理论分析。[6][9]介绍了从1673年惠更斯,胡克直到1868年麦克斯韦(James Clerk Maxwell,1831-1879)一段时期控制理论的早期发展,其中对G.B.Airy (1801-1892,剑桥大学数学及天文学教授)在调速器稳定性分析方面所做的贡献给予了特别的评价。Airy关注调速器的速度控制问题,是因为他需要采用调速器控制望远镜以与地球旋转相反方向做补偿地速的运动,以便长时间观察某一星座[7]。他使用调速器时发现其可能有的不稳定运动:“The machine(If I may so express myself)became perfectly wild” (Fuller引用Airy的1840年论文所述[6]),并采用微分方程的工具对此进行分析。Fuller认为Airy的研究对控制理论的贡献在于引起对控制系统中不稳定现象的关注、提示不稳定问题可以通过系统的微分方程模型来说明,是动态控制系统研究的开端。但由于他的论文写得非常简略,不能判断他当时是否得到了稳定性条件[6]。
人们对宇宙的探索对控制理论的发展起过很大的推动作用,甚至早于牛顿运动定律的发表,天文学家是第一批着手解决动态系统稳定性问题的人员,因为他们需要精确控制大型望远镜的运动,而且他们熟悉太阳系中天体运动的稳定性问题[6]。1893年,俄罗斯数学家A.M. Lyapunov发表了他著名的关于动态系统稳定性的博士论文,建立了非线性时变系统常微分方程理论,这个研究的出发点也是为了研究天体运动的稳定性问题[38]。现代航天工程的发展更是极大地推动了控制理论的发展[1]。
图19、图20可以说明为什么如果想长时间观察某一星座,需要控制望远镜做与地球旋转方向相反的补偿地速的运动。图19为将相机对准天空固定不动长时间不断拍摄获得的照片叠加出的星轨图片,可以看出地球运动对观星的影响,图20则是用赤道仪精确控制相机以与地球转动相反方向以地速转动并长时间不断拍摄,然后将照片进行叠加,则可呈现出肉眼很难看到的美丽的仙女座大星系。
图19. 相机对准天空固定不动长时间不断拍摄的照片叠加出的星轨图片
图20. 赤道仪精确控制相机以与地球转动方向相反以地速转动并长时间不断拍摄,然后将照片进行叠加,则可呈现出肉眼很难看到的仙女座大星系
4. 反馈系统稳定性的理论研究:
麦克斯韦《论调速器》、Routh-Hurwitz 判据
1868年,麦克斯韦的论文《论调速器》(On Governor)系统地分析了几类调速器同时给出了稳定性条件[10],被认为是第一个系统地分析反馈控制系统的理论研究[9]。
上面通过方程(1)~(2)分析瓦特调速器存在稳态偏差的讨论就来自麦克斯韦的论文[10],并进而对Fleeming Jenkin调速器的动态进行了如下建模:
其中P,R,V,F,的定义同(1),G,Y亦为增益系数,W为重物产生的力矩,y为重物的运动。稳态时,调速器的速度为:
说明系统的稳态值与负载R(未知外扰)无关。但系统的稳定是有条件的,只有当
的根都具有负实部时,系统才能到达稳态。
Fuller认为麦克斯韦这篇论文的主要贡献是[9]:
1. 系统地研究动态控制系统的第一篇论文;
2. 采用了线性化技术研究运动系统的稳定性,从而通过特征方程判断系统的稳定性,得到了三阶系统特征方程稳定的判据;
3. 文中例子说明可以设计控制器既消除偏差又不致引起不稳定;
4. 提出了寻找高阶系统稳定性判据的问题。
1948年维纳(Norbert Wiener,1894-1964)为他的学说取名控制论(Cybernetics)就是为了向麦克斯韦的On Governor论文致敬,因为Cybernetics和Governor的希腊文同源[11](见图21)。
图21. 1948年维纳为他的学说取名Cybernetics就是为了向麦克斯韦的 On Governor 论文致敬[11]
当年我第一次了解到第一篇系统分析反馈控制系统的论文作者是麦克斯韦时有点被惊到了,这个麦克斯韦是那个提出著名的电磁麦克斯韦方程的大物理学家麦克斯韦吗?进而好奇他怎么会跑来研究控制问题的?好像是来跨界打酱油的,还竟然一下就做出个开创性的工作,弄了个第一。根据Mayr介绍,在蒸汽机时代,调速器的精度和稳定性问题是一个时髦的问题,困扰了当时的很多科学家和发明家[11],好像麦克斯韦做这个研究只是追逐了一下热点。但我觉得另外几个原因更顺理成章:1863年,作为英国科学促进协会电气标准委员会(British Association for the Advancement of Science Committee on Electrical Standards)的成员,麦克斯韦和H.C. Fleeming Jenkin一起进行了确定电学标准的实验工作,实验中需要控制其中的一个圆形线圈以匀速转动,就用到了FleemingJenkin设计的调速器,麦克斯韦对此印象深刻[7]。另一方面,更早的时候,1857年,麦克斯韦曾以“On the Stability of the Motion of Saturn’s Rings”获得过Adams Prize,他通过把土星环的微分方程线性化,得到一个4阶特征方程,从而可以分析其稳定性。所以他对稳定性问题既有知识储备和积累,又对调速器有直接的了解[9]。
麦克斯韦没有进一步得到更高阶特征方程的根都具有负实部的充要条件,他更大的兴趣还是在电磁学方面,Fuller甚至认为麦克斯韦写On Governor这篇论文就是为了可以让自己从控制问题中脱身,从而专心于电磁学的工作[9]。但他把确定高阶特征方程的根都具有负实部的充要条件这一问题明确地提了出来,希望得到数学家的关注。在科学的发展中,准确地提出问题和解决问题同样重要。
麦克斯韦提出的问题被他剑桥大学三一学院的校友劳斯(E.J. Routh,1831-1907,英国数学家)解决了 (1854年,劳斯与麦克斯韦以第一和第二的成绩毕业于剑桥三一学院[7])。
1877年,劳斯得到特征方程所有根都有负实部的多项式系数条件,Adolf Hurwitz (1859-1919,德国和瑞士数学家) 1895年也独立地推出了这个判据,因而它被称为 Routh-Hurwitz 判据。
1877年 Adams Prize(麦克斯韦为评奖委员会委员)的主题是动态稳定性的判据(the criterion of dynamical stability),劳斯获得了此奖,他解决了麦克斯韦提出的判断所有根都有负实部的多项式系数条件[12]。
当时解决这个问题的代数工具已经被Augustin-Louis Cauchy,Charles Sturm和C.Hermite等人建立起来,Routh综合运用这些结果得到了动态系统稳定性理论[12,13]。
虽然麦克斯韦和劳斯对调速器稳定性分析的结果可能并没有对具体改进离心力调速器的设计起到直接作用[11,14],但对控制科学有很大贡献,线性化技术与特征方程分析至今仍是控制系统稳定性分析的一个重要手段。
5. 反馈控制器的大量应用:
船的自动驾驶仪、PID控制器、
频域方法、防空控制、经典控制理论等
19世纪后半叶至20世纪初,反馈控制器被大量应用,包括电压、电流与频率的调节、蒸汽发电中的锅炉控制、电机的速度控制、船与飞行器的驾驶与镇定、过程工业中的温度、压力与流量控制等等[1]。随着控制系统用于许多不同的工程领域,特别是一些复杂的机械装置,如船的自动转向装置和锅炉控制(涉及液面、汽压等多变量控制问题),控制设计问题变得突出起来,这时存在的主要问题有:缺乏通用语言来从理论上理解动态系统的控制问题,缺乏简单的、容易运用的分析与设计方法。唯一可用的分析工具似乎只是微分方程和当时还不太广为人知的Routh-Hurwitz稳定性判据,但应用这个判据需要获取系统参数值,而且难以具体指导如何设计出使系统稳定的控制器[1]。
一些聪明的工程师如Elmer Sperry (1860-1930,美国发明家、企业家)敏锐地注意到人进行控制调整时不是简单地采用开关控制(On-off Approach),而是综合运用了预测、当被控量接近目标值时撤出控制、以及当存在持续的偏差时进行小幅度的慢慢调节等方法,于1911年设计出的采用较为复杂控制律——PID控制结合自动增益调整——的船舶自动驾驶仪[1],被认为是最早发明的PID控制器。
1922年,Nicholas Minorsky(1885-1970,俄国和美国工程师,应用科学家)从理论上清晰地分析了船在常值扰动下的自动驾驶问题,推导出了PID控制器形式[1,15]。
Minorsky将船自动驾驶中的方向稳定性问题用如下动态模型描述[15,45]:

其中α为船舶与指定航线间的偏差角,A和B分别为转动惯量和阻力力矩系数,D为常值扰动力矩,ρ为舵转角,是可以设计的控制量,k为舵增益系数。因为航向即使存在很小的稳态误差,也会造成“失之毫厘谬之千里”的后果,因此,Minorsky考虑的控制问题是:当存在常值扰动D时,如何改变舵转角ρ把航向偏差α控制到零[45]。他分析了5种不同的控制策略,然后得出当把舵的转向速度按如下方式:
改变时,可以在常值扰动下,将航向偏差α稳定地控制到零。而(8)按现在的表述就是:
即为偏差的Proportional(比例)—Integral(积分)—Derivative(微分)(PID)三项控制律(如图22)。

图22. Minorsky从理论上分析了船舶自动驾驶问题,推导出了PID控制形式
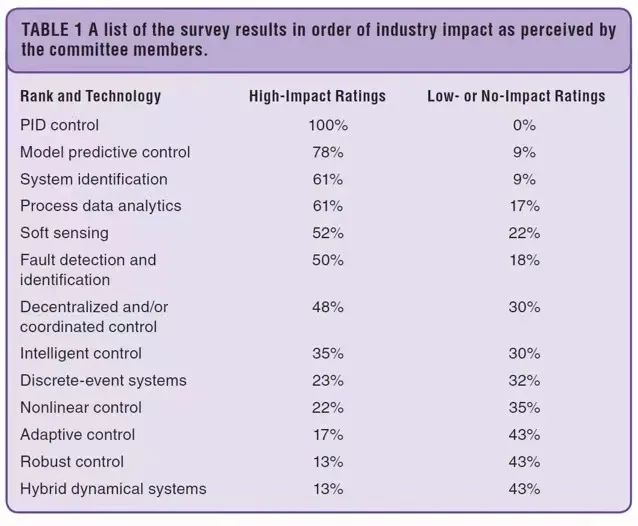
PID是迄今为止应用最广泛的一种控制方法,目前95%以上的过程控制回路和90%以上的航空航天控制回路还都是基于PID控制。2017年国际自动控制联合会(International Federation of Automatic Control,IFAC)的工业委员会对工业技术现状进行了调查,在十几种控制方法中,PID以百分之百好评(零差评)的绝对优势居于榜首(见图23)[16]。
图23. 2017年IFAC工业委员会对工业技术现状进行了调查,PID以绝对优势居于榜首[16]
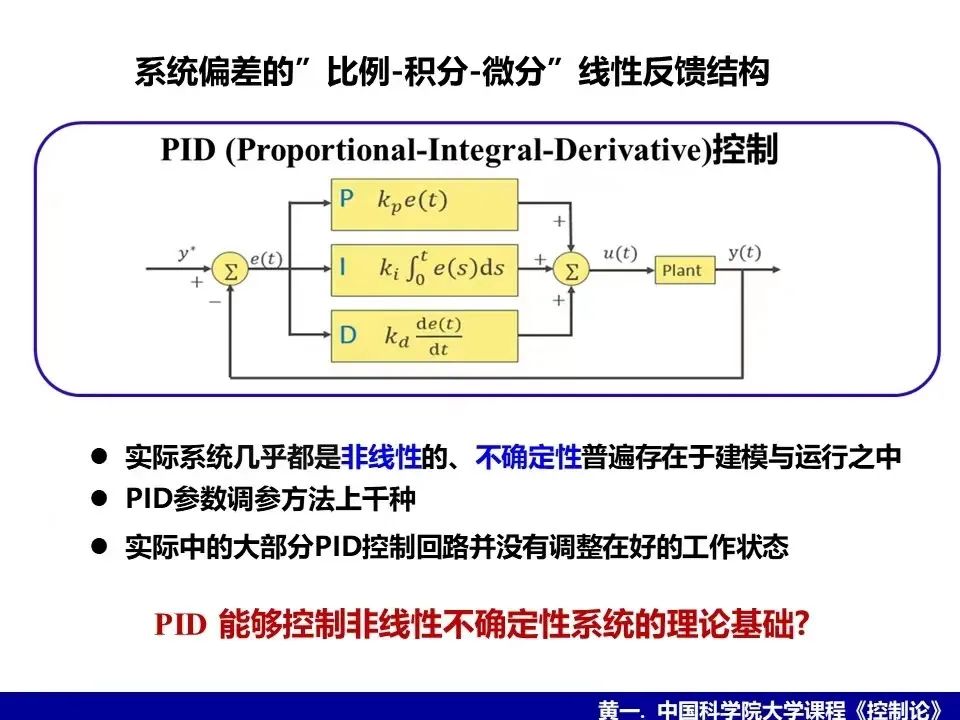
其实PID控制器的结构非常简单,就是系统偏差的“比例-积分-微分”三项线性反馈结构之和 (如图24),而实际系统几乎都是非线性的,而且不确定性普遍存在于实际系统的建模与运行之中,那么简单的线性结构的PID控制为什么能在实际中广泛应用于非线性不确定系统,它的理论基础是什么?另虽然PID只有三个参数,但至今PID调参方法已有上千种,都是经验公式,而工程界依然认为实际中的大部分PID控制回路并没有调整在好的工作状态[17,18],那么如何调整才能达到令人满意的效果?这些可以说是控制理论中最基本的问题,一百多年来一直没能从理论上给以很好回答。这一问题近年获得一些突破性进展,[19][20]对PID控制的广泛性给出了理论回答,而通过研究某种自抗扰控制(Active Disturbance Rejection Control,ADRC)1的具体形式与PID控制的内在联系,一种可使PID具有自抗扰能力的新的定量调参方法被进一步提出来[21],新的PID调参方法是由ADRC启发而来,并不是直观容易想到的,但其物理功能却比原PID的三个参数更明确而易于整定(如图25)。
图24. PID控制器:系统偏差的“比例-积分-微分”线性反馈结构
*1. 自抗扰控制由中国科学院系统科学研究所韩京清研究员于20世纪年代提出,正式发表于1998年,作为在PID控制基础上的创新,其强大的鲁棒性和突出的瞬态响应性能,吸引着越来越多的关注,已发展为一种可解决具有大范围及复杂结构的不确定系统控制问题的有效方法[22-24]。
20世纪20~40年代,控制系统分析与设计的研究在不同国家的不同小组独立进行,在美国,最有影响的几项工作主要来自于以下几个群体[1]。
第一个群体是贝尔实验室(AT&T BellLabs)的工程师以及科学家,发展出控制系统分析与设计的频域方法。
故事要从布莱克(Harold Stephen Black, 1898-1983, 美国电气工程师)在1927年发明负反馈放大器说起(“反馈(feedback)”一词被正式使用[7])。
第一次世界大战后,随着电子放大器的出现,远距离通话成为可能。距离增加,电能损耗也增加。为了增加传输距离,需要用直径较大的传输线或增加放大器的个数,但放大器个数越多,因非线性以及噪声造成的失真越大。1920年前后,放大问题已经成为开发长距离电话技术的一个严重阻碍[1]。
布莱克当时是AT&T的工程师,他深入研究了这个问题,他发明的负反馈放大器通过把输出的放大信号再反馈回输入端,就可以减小由于噪声和器件参数漂移造成的失真[25](见图26)。
图26. Black 发明的负反馈放大器抗扰原理[25]
虽然反馈的原理在公元前300年古希腊人和阿拉伯人发明的浮球调节装置、17世纪的温度调节器、18世纪工业革命的标志——瓦特蒸汽机中采用的飞球式调速器中就存在,但“反馈(feedback)”一词被正式使用则是在布莱克发明负反馈放大器时。
关于布莱克的这个发明,有个被大家津津乐道的故事:1927年8月2日,布莱克上班途中,在Hudson河的渡船Lack awanna Ferry上灵光一现,想出了在控制发展历史上具有重要意义的负反馈放大器。由于手头没有合适的纸张,他将这个灵感记在了一份纽约时报上,这份报纸已成为一件珍贵的文物珍藏在AT&T的档案馆中[26,27,28]。(注:在8月6日周六的上班途中,布莱克在渡船上再次在当天的一份纽约时报上写了更详细的过程(见图27))。
图 27. Black 负反馈放大器的灵感来自于上班途中的灵光一现,只能将其记录在手头的纽约时报上[27]
但其实为了这个灵光一现,布莱克持续不断地努力了6年。1921年,Black毕业于伍斯特理工学院(Worcester Polytechnic Institute),随后到贝尔实验室工作。作为新人,他希望尽可能多地了解公司的业务,于是查阅了大量公司文档,发现公司当前遇到的主要问题是如何使放大器可以串联起来把信号稳定无失真地传到千里之外。于是,他要求承担这项工作,他上司说“可以,但在不影响分配给你的其他工作的前提下”[26]。于是,最初的两年,他利用周末和晚上的时间阅读了所有能找到的关于非线性电路方面的材料以及公司的有关文档,后4年则几乎无时无刻不在琢磨怎么实现一个具有线性功能的放大器,在对放大器问题进行了几年艰苦的研究之后,这才有了1927年8月2日上班路上的灵光一现[26]。
而从负反馈放大器的发明到其实际应用则又经历了一段充满荆棘的漫长路途[27]。
为了减小失真(误差)而引入的反馈装置,有可能会使得系统发出尖叫(Singing/Oscillating)而变得不稳定[27](反馈的代价:系统复杂了,可能造成系统不稳定)。这又涉及到了麦克斯韦和劳斯研究过的稳定性问题,但这时,系统的动态特性已经很复杂(通常是几十阶的高阶微分方程),Routh-Hurwitz 判据很难再有帮助[5]。贝尔电话实验室的通信工程师和科学家们开始考虑用频率响应(Frequency Response)和复变函数理论进行分析,发展出了控制系统分析与设计的频域方法[1,5]。
负反馈放大器的发明及其发展被认为是发明家、工程师与受过良好数学物理训练的理论研究团队成功合作的杰出案例[27],其中有两个代表性人物:哈里·奈奎斯特(Harry Nyquist,1889-1976)和亨德里克·博德(Hendrik Bode,1905-1982)。
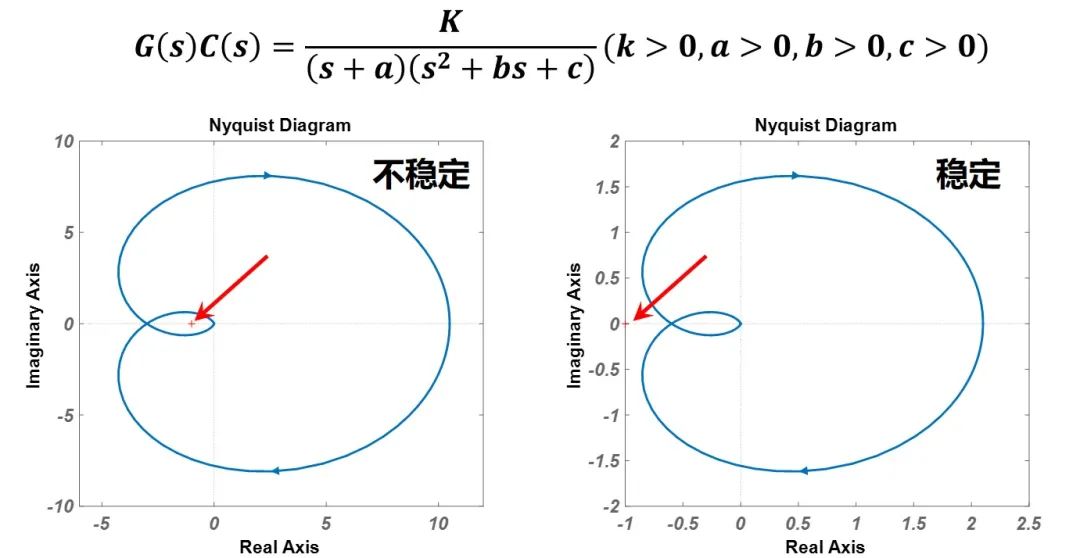
Nyquist1917年获得耶鲁大学物理学博士学位,1917-1934年就职于AT&T。1928年,Nyquist与AT&T的其他一些工程师一起与布莱克商讨如何将负反馈放大器用于一种新的电缆通信系统。他做了负反馈系统的分析,并最终在频域上建立了一个与已有工作完全不同的稳定性判据——Nyquist判据[27],Nyquist判据可以直接指导如何调整控制器确保系统稳定[29](见图28)。
图 28. Nyquist 在频域上建立了一个与已有工作完全不同的稳定性判据-Nyquist 稳定判据
H.Bode 1926年获得俄亥俄州立大学(Ohio State University)数学硕士学位,然后就职于贝尔实验室,期间又于1935年取得哥伦比亚大学(Columbia University)物理博士学位。1928年,在开发一种新的同轴电缆通信系统时,Bode带领一组数学家研究能充分利用Black放大器优点的系统设计方法。1940年,Bode在其经典论文“Relations Between Attenuation and Phase in Feed back Amplifier Design”中进一步提出了利用频域的Bode图、幅值裕度/相位裕度等相对稳定性概念来设计负反馈放大器的方法,并指出了系统增益与带宽的极限关系[30](见图29)。
图29. Bode 图:通过频域的幅值裕度/相位裕度分析系统稳定性
二战中,Bode参加了高射炮控制系统的研制,他参与研制的高射炮在1944年的安齐奥战役(Battleof Anzio)和诺曼底登陆时都发挥了很大的威力。他的研究工作一直持续到美国太空计划时代,是一位在学术界广受尊重的科学家[31]。Bode去世后,1989年IEEE控制系统协会(IEEE Control System Society,IEEE CSS)设立Bode Lecture Prize以表彰对控制系统科学和工程做出突出贡献的人。2019年中国科学院系统控制重点实验室郭雷院士“因在自适应控制、系统辨识、自适应信号处理、随机系统及应用数学领域的根本性和实际性贡献”被授予Bode Lecture Prize,是该奖设立30年以来,中国和世界华人中第一位获此荣誉者[43](见图30)。
图30. 2019 年中国科学院系统控制重点实验室郭雷院士被授予 Bode Lecture Prize,是该奖设立 30 年以来,中国和世界华人中第一位获此荣誉者(图中郭雷院士,左一和右一分别为2018、2019 IEEECSS 主席 Francesco Bullo 教授和 Robert R. Bitmead 教授)
贝尔实验室的工程师以及科学家团队的这些工作最终发展为控制系统分析与设计的频域方法。
控制系统分析与设计的频域方法至今还是控制工程师们最喜欢和信赖的一种方法,仍然在广泛应用。频域方法可以摆脱处理微分方程的困难,直接通过系统频域响应的实验数据进行控制系统的分析与设计[1]。还有一个重要原因是,虽然稳定性是控制系统设计中首要的问题,但系统仅有稳定性是不够的,一个好的控制系统除了需要具有稳定性外,还应兼顾快速、准确性、抗扰性等可能彼此冲突的性能指标,频域设计可以比较清楚地通过系统的频率响应Bode图同时在不同频段兼顾各项指标进行设计,简明而直接(见图31)。
图31. 控制系统多项指标可以通过频域方法简明且直接地进行分析与设计
20世纪30-40年代,美国过程工业中的工程师和科学家开始系统地建立和开发控制系统设计方法,一个代表性工作是J.G.Ziegler和N.B.Nichols在1942年提出的PI及PID控制的参数整定方法,后来被称为Ziegler-Nichols调整法[1]。
第三个群体在麻省理工学院(MIT)的电子工程系,设计了微分方程模拟计算机,进行控制系统仿真。
1930s,Vannevar Bush在MIT带领Harold Hazen,Gordon Brown和Claude Shannon设计了微分方程模拟计算机(the Differential Analyzer)(如图32),从而可以进行动态系统仿真[1]。其后,Harold Hazen和Gordon Brown领导的小组利用模拟计算机进行了控制系统的时域仿真[1]。
图32. 1930s, Vannevar Bush 在 MIT 领导设计了微分方程模拟计算机(the differential analyzer)[32]
关于控制系统的计算机仿真这项工作要不要在控制发展史里介绍我自己也反复过几次,中间有几次上课没有讲。后来,发现控制室的学生大多本科是学数学的,不太喜欢计算机仿真,反而觉得有必要给学生们强调一下计算机仿真的重要性。随着计算机技术的快速发展,计算机仿真在控制研究中已经发挥着越来越重要的作用,不仅仅是指学术论文中那种简单的仿真,虽然现在仿真已经是大部分论文中的一个重要环节,计算机仿真更重要的价值还在于:
• 可以直接启发新的研究思路和灵感,当然由仿真启发的新方法还需要经过艰难的严格理论论证和严苛的物理实验的考验。
• 论证控制方法的重要手段。如今控制问题变得越来越复杂,需要考虑的因素越来越多,传统的理论分析手段难以彻底解决问题时,详尽充分的计算机仿真已成为论证控制方法的重要手段。比如,在航天工程中研究新的飞行方案时,稳定裕度分析往往还需要结合大量拉偏参数以及考虑各种物理器件约束的计算机动态仿真验证。因此,我们也许应该思考理论分析的内涵是不是也应该与时俱进。
二战的爆发使控制系统的工作集中在几个特定的问题上,最重要的一个是防空高射炮瞄准系统(Aiming of Anti-aircraft Guns)。这是一个复杂的问题,需要完成快速发现飞行目标、准确预报飞行目标的位置、精确瞄准等一系列动作。为了完成这个任务,需要将雷达跟踪系统(Automatic Tracking Radar System)直接与射击指挥仪(Gun Director)并最终与炮火位置控制器(Gun Position Controller)相连。为此,美国集中了当时机械、电力电子、通信等各方面的工程师和科学家通力协作来完成这一系统,如SCR-584雷达系统(SCR-584 Radar System)由MIT雷达实验室研制,M9射击指挥仪(M9 Director)则由贝尔实验室集合C.A.Lovell, D.B.Parkinson, Bode, R.C.Blackman, Claude Shannon等人研制(见图33)。这是一次成功的合作,这个系统在1944年6月-8月英国东南部抗击德国V-1火箭空袭的战斗中获得了很高的成功率,击落了上千枚V-1火箭[1,33]。
图33. MIT 雷达实验室研制的 SCR-584 雷达系统(上)[34],Bell 实验室研制的 M9 指挥仪(下)[40]
V-1火箭被认为是第一个可操作的自动化机器炸弹2(the First Operational Robot Bomb),飞行速度快且高度低,对炮火有很强的抵抗力[33]。1944年的伦敦空战被认为是自动机战争的开端(the Beginning of the First Battle of the Robots):由SCR-584雷达、M9射击指挥仪、炮台组合成自动控制系统发射带有近身引信(the Proximity Fuze)的VT(Variable Time)robot与V-1robot的抗争[33,35]。
* 2. 2018 年 7 月,苏剑波邀请高志强和我在上海交大讲授了一次“自抗扰控制技术”的暑期课程,其中有个单元是苏剑波讲机器人,他的开场白让我印象深刻,说他读硕士学位时曾经不喜欢机器人这个方向,因为觉得“那时的 robot 根本就没人样!”。这里把 robot 翻译成机器人似乎也不合适,翻了下字典,robot 原文为能自动运动的机器(a mechanism that can move automatically)。
战后,经典控制技术基本建立起来了[1],是一种针对单输入线性定常系统的设计方法。主要有以微分方程描述的系统特征根、以及上升时间、超调、稳态误差和阻尼等指标表述系统性能的时域方法,和以带宽、谐振、幅值/相位裕度以及频域响应图展示系统行为的频域方法,有人喜欢时域方法,因为可以直观了解系统的实时行为,而二战中的工作充分显示了频域响应方法在反馈系统设计上的威力[1]。
战争中解决防空控制问题的经历也使人们进一步认识到[1]:
1.将几种由不同小组设计的部件集成在一起工作时,整个系统的性能就不那么依赖各个独立单元的性能,而在于它们是否能很好地协同工作。
2.无论是通信工程师擅长使用的频域方法还是机械工程师喜欢的时域方法都不足以完成设计,所需要的是能综合两者优点的方法。
3.基于线性和确定性假设进行的控制系统设计存在局限,因为,实际系统都是非线性的,测量包含误差和噪声,过程和环境存在不确定性,带宽的约束、噪声的影响以及非线性特性都会给系统设计带来困难。
6. 防空控制问题与维纳的“Cybernetics”
和钱学森的“Engineering Cybernetics”
1940-1945年5年内,美国国防研究委员会火控部(Fire Control Division,National Defense Research Committee)一共资助了80个研究项目,经费数目最大也是最成功的一个($1.5million)是贝尔实验室的M-9射击指挥仪,经费最少的一个项目($2325)是给维纳的“预测目标飞行模式(How to Predict Flight Patterns)”[35],维纳从随机系统的角度进行研究[1]。虽然维纳的项目研究并未真正用于实际,但这个工作促使他进一步思考有关反馈、信息、控制、输入、输出、自我平衡、预测和滤波(Feedback, Information, Control, Input, Output, Stability, Homeostasis, Prediction, and Filtering)等问题[41],并最终创立Cybernetics(1948年出版了Cybernetics这本著作[42](见图34))。维纳的 Cybernetics 学说既有理性的抽象概念如控制、反馈,也有丰富的想象力,如在人机关系方面,人与机器的融合,将机器拟人化以及将人机械化。Cybernetics发表后,马上被认为是一种新思想甚至新兴学科,而吸引了工程、数学、生物、心理甚至社会、哲学、政治等众多领域的极大关注[35]。
许多人认为维纳的Cybernetics不应该翻译成“控制论”,从书名(见图34)就可看出Cybernetics具有控制、通信以及人机交互等多重含义,翻译成“控制论”只取了其中控制的部分。现在人工智能又热了起来,也有人认为维纳的Cybernetics其实描述的就是人工智能。
1954年,钱学森(1911-2009)以火箭的控制与制导(Controland Guidance)等相关实际问题为应用背景,在美国发表了具有更多数学描述的工程控制论(Engineering Cybernetics)[51,49](见图35)。该书是钱学森在美国因政治迫害而被强迫滞留美国并部分失去自由的情况下完成的。
图35. 钱学森所著 Engineering Cybernetics
1945年5月,钱学森加入美国空军科学咨询团,赴欧洲考察德国航空、火箭技术的发展情况,德国之行让钱学森深刻意识到控制与制导的重要性。1950年之后,当他因政治迫害而无法再继续参与军事科技研究后,即将学术重点转移到这一新兴的理论领域,进行工程控制论的研究[50]。
钱学森在序言中阐明工程控制论的目的是想建立有别于具体“工程实践(Engineering Practice)”的“工程科学(Engineering Science)”,以使我们可能以更广阔的眼界和更系统的方式观察问题,从而可能给出解决老问题的富有成效的新方法,并揭示新的、意想不到的前景。钱学森既强调数学对于工程科学研究的重要性,又强调重在运用恰当的数学工具研究解决实际工程问题而非囿于严格精巧的数学论证[46,47,48]。
1955年,经过中国政府努力,钱学森终于回到祖国。回国后,他提议并带领了中国航天事业的发展,还努力推动控制科学在中国的发展。1956年,钱学森亲自给中科院的一些研究所以及北京大学和清华大学等高校教师和学生讲授“工程控制论”[48,49]。1962年,在钱学森的倡议下,经中国科学院与国防部第五研究院商定,在中科院数学研究所成立控制理论研究室(即中国科学院系统控制重点实验室前身),数学家关肇直和控制学家宋健任首任正副主任,宋健带领国防部五院的研究人员到研究室共同工作。这是我国最早从事现代控制理论研究的单位,致力于为我国的国防尖端技术服务并在中国推广普及现代控制理论[52]。
战后控制科学的发展更主要地受到两大因素的推动:一是美苏太空竞赛,二是数字计算机的出现,可以完成复杂的计算和动态系统仿真[1]。航天任务需要研究解决导弹与太空飞行器的发射(Launching)、机动(Maneuvering)、制导(Guidance)及跟踪(Tracking)等问题,这个问题的特点是物理模型可以用一组一阶微分方程(线性或非线性)描述,再就是航天器上装有具备良好精度的测量装置(传感器)用于状态测量、轨迹规划,于是发展出状态空间方法[1]。
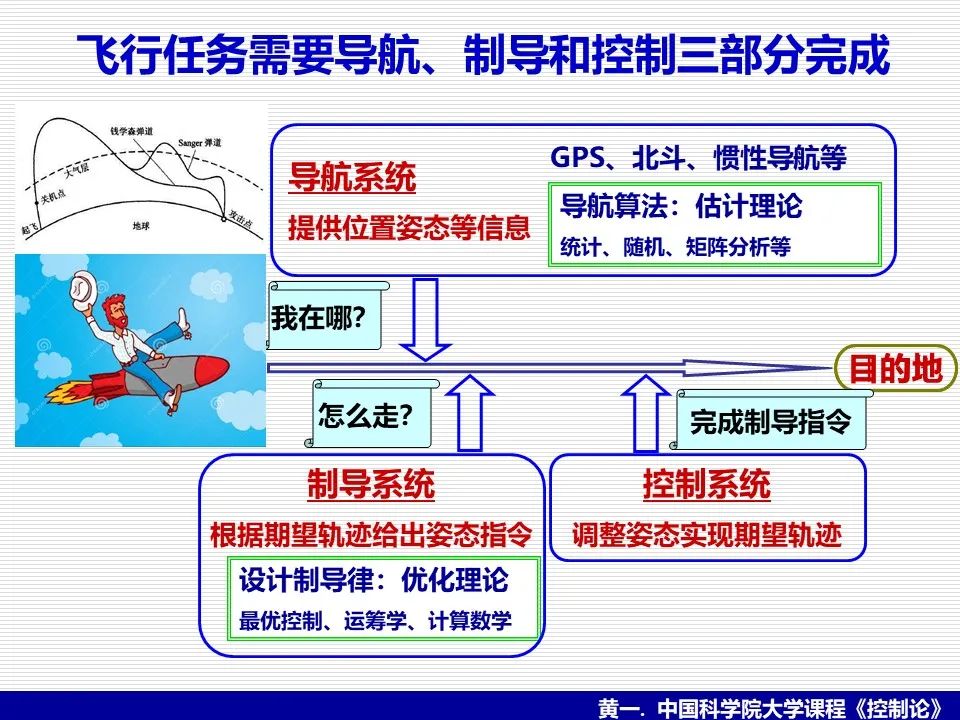
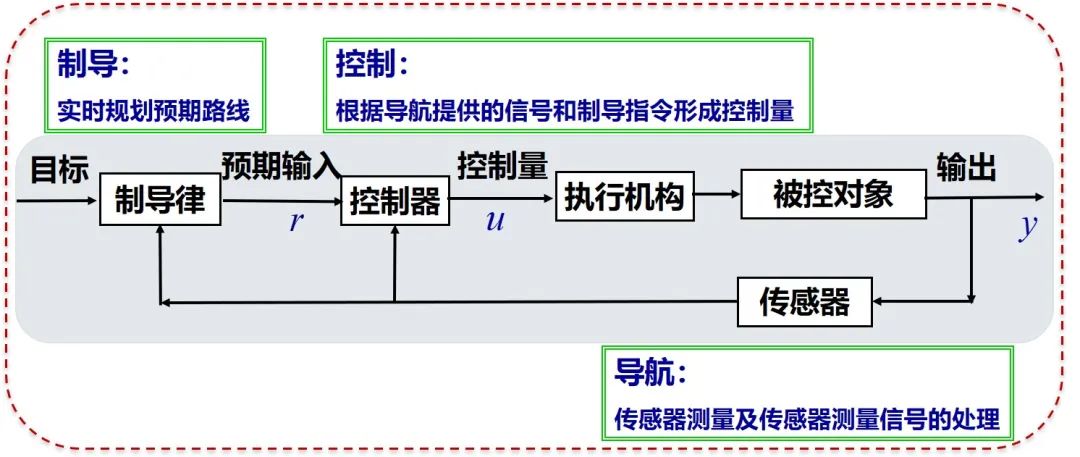
航天控制系统比以往的控制系统复杂多了。图5展示过控制系统的几个基本组成,在最初的简单控制系统里,如水钟、飞球式调速器,测量、控制器、执行机构是一体的,控制目标也比较简单。而航天的控制系统跟以往控制系统相比要复杂得多,飞行任务往往需要导航、制导和控制三部分协同完成(见图36)。对应于图5的控制系统基本组成框架,导航系统相当于测量部分,完成传感器测量及传感器信号的处理,以实时准确地提供飞行器在飞行当中的各种状态(位置、速度、姿态、角速度等);制导系统对应于给出预期运动指令的部分,根据飞行最终任务实时规划出当前飞行状态需要如何调整的指令值(通常为姿态指令),此时,期望输入是实时生成的而不是事先确定的;最后的关键就是控制系统根据导航系统提供的当前飞行状态和制导系统提出的运动指令形成控制量调整飞行状态(如图37)。
图36. 航天飞行任务往往需要导航、制导和控制三部分完成
图37. 导航、制导和控制与控制系统各基本环节的对应关系
航天任务的需求强力推动了现代控制理论的发展,贝尔曼的动态规划、庞特里亚金的极大值原理和卡尔曼滤波被认为是现代控制理论的三个代表性工作。1948年-1952年,贝尔曼 (Richard Bellman, 1920-1984)在兰德公司(Rand Corporation)数学部工作,他在研究解决导弹部署以达到最大破坏力问题的过程中,提出了“最优性原理(Principle of Optimality)”和“动态规划(Dynamic Programming)”[1]。庞特里亚金(Lev Semenovich Pontryagin, 1908-1988)是苏联数学家。航天飞行任务除了落点精度的要求外,系统性能还涉及一些其他限制:如时间最短或燃料消耗最少等,Pontryagin 1956年提出的极大值原理是关于这类最优控制问题的理论基础[1]。Kalman 滤波则是从带有噪声以及不完全测量的信号中提取所需信号的一种数学算法,Kalman 滤波刚提出时曾受到很大质疑,直到1960年,卡尔曼(Rudolf Emil Kalman, 1930-2016)访问 NASA Ames 研究中心,其后Kalman滤波成功地在阿波罗登月计划中得以应用[36]。
文献[1]把现代控制理论的起点放在1956年,那年在德国海德堡召开了一次自动控制的国际会议,很多国家的学术与工业界代表参加了会议。会上,一些代表提议成立一个国际组织来推动自动控制的发展,就是1957年9月在巴黎正式成立的国际自动控制联合会(IFAC),前苏联申请了1960年在莫斯科召开第一次IFAC世界大会。因此,也有人把1960年第一届IFAC世界大会的召开作为现代控制理论起点的一个重要标志。IFAC是一个以国家组织为其成员的国际性学术组织,中国为其创始成员国,钱学森代表中国被推选为第一届IFAC理事会成员。
1960年6.27-7.2,第1届IFAC世界大会在莫斯科召开,约1500名控制工程师和科学家齐聚莫斯科,会上有285篇论文进行了交流,不乏经典之作,如[37]:
•Boltyanski, Gamkrelidze, Mishchenko, and Pontryagin:“The Maximum Principle in the Theory of Optimal Processes of Control”
•R.Bellman and R.Kalaba:”Dynamic Program and Feed back Control”
•R.E.Kalman,“On the General Theory of Control Systems”
此后,IFAC世界大会每3年举办一次,1999年第14届IFAC世界大会在北京召开。
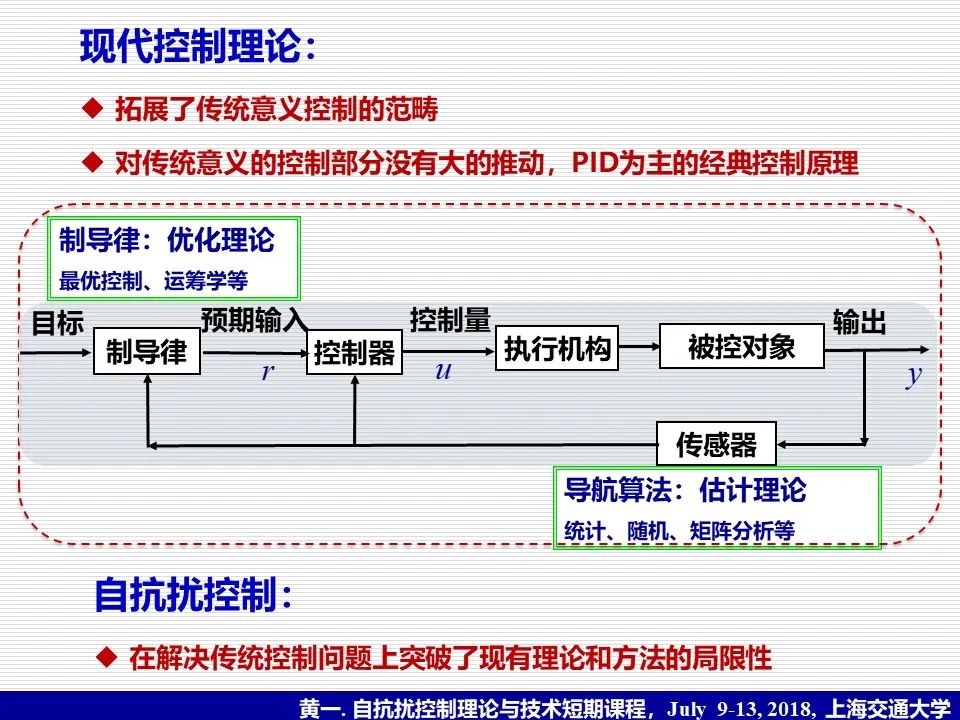
读到这段历史时,我总感觉以一次会议或组织的成立作为一个学科新阶段的起点似乎理由不够充分,还是更应该看有什么新进展。为什么上述三项工作被称为现代控制理论的代表性工作,是我在研究生刚入学时就有的问题,几十年了,而现代控制理论在这几十年里也饱受不接地气的批评。2017年接到给北京五中学生以“数学与航天”为题讲一次课的任务,苦恼了很久,不知从哪破题,苦思冥想中,忽然对自己这个几十年前的问题有了不同的认识。追根朔源,Kalman 滤波比较好地解决了航天导航系统里的信息处理问题,而最优控制其实是期望解决航天制导系统的实时轨线规划问题。因此,根据图35中导航、制导与控制的关系,这三个代表性工作并不是解决传统意义上的控制问题,而是传统控制中没有涉及的部分,即状态信息的提取和控制输入指令的规划。所以,可以说现代控制理论拓展了传统意义下控制研究的范畴,但对解决传统意义上的控制问题没有大的推动,依然是以PID为主的经典控制技术占主导,而现代控制理论里那些试图解决传统意义上控制问题的尝试似乎都不太成功,这是需要我们深思的(见图38)。前面提到的自抗扰控制则汲取并拓展了现代控制理论信息处理中状态的概念和观测器的方法,在解决传统控制问题上突破了现有理论和方法的局限性。作为在PID控制基础上的创新,自抗扰控制已经实际应用于我国航空航天多个新型飞行器的飞行控制,以及我国一些电厂的控制回路中[24,44],而其未来的发展,也许应该思考如何拓展到更广的领域。
图38. 现代控制理论拓展了传统意义下控制研究的范畴
走马观花地回顾了控制发展历程之后,历史给我们哪些启发呢?我自己的几点感受是:
Maxwell 系统地分析反馈控制稳定性的工作是具体针对当时调速器的稳定性问题,引申发展出来的;Black, Nyquist 和 Bode 等人的频域分析与设计方法是为具体解决通讯快速发展中出现的稳定性问题而发展起来的,甚至现代控制理论也是由于太空计划中的一系列难题推动的。因此,控制的研究要针对实际问题,对所研究的问题要有透彻的了解,在创造性地解决问题中做出原创性的工作。
2. 历史人物天才式贡献的背后是对钻研的热情和持续不断的努力
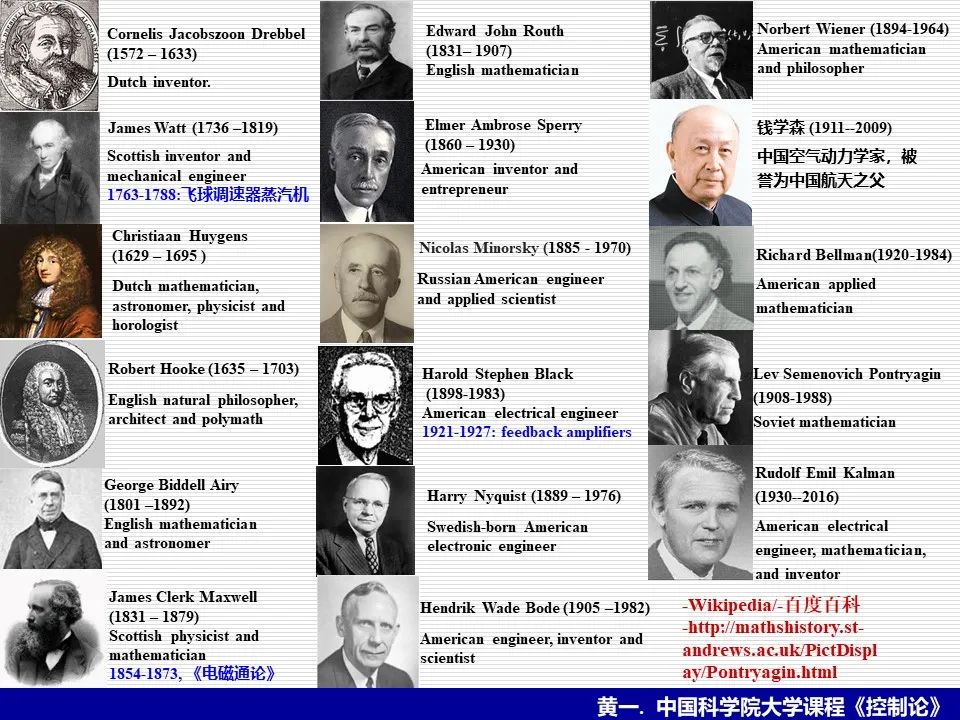
走马观花中愉快地在历史人物间穿行,流连忘返(图39),被他们带着去探索各种问题,这是特别吸引我的部分,常常会有”他是怎么想出来的”的好奇,在这个过程中既感叹于他们的博学和才华,也被他们钻研的热情和执着所打动,任何一点进展都不是一蹴而就的。
图39. 穿行在历史人物间,被他们带着去探索 (人物图片来自网络)
3. 控制系统的研究通常在时域/复数域/频域多个域中展开
时域的状态空间和微分方程分析,复数域的传递函数和零极点分析,以及频率域的带宽和幅值/相位裕度分析,每一种方法都有其适用的范围、优点和局限,最好能综合掌握、灵活运用。
回头看,精彩纷呈,向前望,道路宽广却山长水远,继续上路吧。
致谢:本文初稿 2020 年 4 月在公众号“自抗扰控制”发表,接受了一次“云审稿”,得到许多鼓励和中肯的意见,特别是郭雷院士和北京大学王龙教授还就一些内容的完善进行了多次讨论,给出许多具体建议,在此表示衷心感谢!
走马观花看控制发展简史课程回放链接:https://campus.swarma.org/course/5313
黄一,中国科学院系统控制重点实验室研究员,中国自动化学会控制理论专业委员会委员。主要研究领域为不确定系统的估计与控制。
[1]Stuart Bennett. A brief history of automatic control. IEEE Control Systems, 1996, 16(3): 17-25.
[2]Michael K. Masten. President’s Message. IEEE Control System, 1996, 16(3): 4.
[3]Richard C Dorf and Robert H Bishop. 现代控制系统
[4]Mayr O. The Origin of Feedback Control. Cambrige, MA: MIT Press, 1970.
[5]Gene F Franklin, J David Powell and Abbas Emami- Naeini. 动态系统的反馈控制(第7版),机械工业出版社, 2016
[6]Fuller A T. The early development of control theory. J Dyn Sys Meas Control, 1976, 98: 109-118.
[7]Bennett S. A history of control engineering 1800- 1930, Stevenage: Peter Peregrinus, 1979.
[8]张伟伟. 图说蒸汽机发展演变的三个阶段. 系统与控制纵横,2017, 4(2):45-58.
[9]Fuller, A.T. The early development of control theory (II). J Dyn Sys Meas Control, 1976, 98: 224-235.
[10]Maxwell, J C. On governors. Proceedings of the Royal Society, No 100, 1868.
[11]Mayr O. Maxwell and the origins of Cybernetics, Isis,
[12]Fuller A T. Editorial of Routh Centenary Issue. Int J Control, 1977, 26: 167-168.
[13]黄琳. 稳定性与鲁棒性的代数基础. 科学出版社, 2003.
[14]Trinks W. Governors and the governing of prime movers. London: Constable and Co., Ltd., 1920
[15]Stuart Bennett. Nicolas Minorsky and the automatic steering of ship. IEEE Control Systems, 1984, 4(4): 10- 15.
[16]Samad T. A survey on industry impact and challenges thereof. IEEE Control Systems Magazine, 2017, 37(1): 17-18.
[17]O’Dwyer A. PI and PID controller tuning rules: an overview and personal perspective. Proceedings of the IET Irish Signals and Systems Conference, pages 161- 166, 2006.
[18]Åström K J, Hägglund T. PID Controllers: Theory,
Design and Tuning, 2nd ed. Research Triangle Park: Instrument Society of America, 1995.
[19]Zhao C, Guo L. PID controller design for second order nonlinear uncertain systems, Science China, Information Science, 2017, 60(2): 022201:1-022201:13.
[20]Zhang J K, Guo L. Theory and Design of PID Controller for Nonlinear Uncertain Systems. IEEE Control Systems Letters, 2019, 3(3): 643-648.
[21]Zhong S, Huang Y, Guo L. A Parameter Formula Connecting PID and ADRC. Science China, Information Science, 2020, 63(9): 192-203. https://doi. org/10.1007/s11432-019-2712-7 .
[22]韩京清. 自抗扰控制器及其应用. 控制与决策,1998, 13(1): 19-23.
[23]Han J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron., 2009, 56(3): 900- 906.
[24]Huang Y, Xue W. Acitve disturbance rejection control: methodology and theoretical analysis. ISA transactions, 2014, 53(4): 963-976.
[25]Black H.S. Stabilized feedback amplifiers, Electrical Engineering, 1934, 53: 114-120.
[26]Black H.S. Inventing the negative feedback amplifier. IEEE Spectrum, 1977, 14: 54-60.
[27]Kline R. Harold Black and the negative-feedback amplifier. IEEE Control Systems Magazine, 1993, 13(4): 82-85.
[28]王庆林. 自动控制理论的早期发展历史. 自动化博览,1996, 14(5): 22-25.
[29]Nyquist H. Regeneration theory. Bell System Technical Journal, 1932, 11: 126-147.
[30]Bode H W. Relations between attenuation and phase in feedback amplifier design. Bell System Technical Journal, 1940, 19: 421-454.
[31]https://en.wanweibaike.com/wiki-Hendrik%20Bode
[32]Bush, V. The differential analyzer. A new machine for solving differential equations. Journal of the Franklin Institute. 1931, 212 (4): 447-488.
[33]Mindell David A. Automation’s Finest Hour: Bell Labs and Automatic Control in World War II. IEEE Control Systems Magazine, 1995, 15(6): 72-80.
[34]https://en.wanweibaike.com/wiki-SCR-584%20radar
[35]Thomas Rid. Rise of the machine, a cybernetic history. W.W.Norton & Company, Inc. 2016.
[36]https://en.wanweibaike.com/wiki-Rudolf_E._Kalman
[37]Stephen Kahne. A history of the IFAC congress, IEEE Control Systems, 1996
[38]Park P C. A.M.Lyapunov’s stability theory-100 years on, IMA Journal of Mathematical Control & Information, 1992, 9(4): 275-303.
[39]https://en.wanweibaike.com/wiki-Watt_steam_engine
[40]https://www.computerhistory.org/revolution/real-time- computing/6/124/519
[41]Hans Freudenthal, Norbert Wiener. Biography in Dictionary of Scientific Biography(Encyclopedia.com), http://mathshistory.st-andrews.ac.uk/DSB/Wiener_Norbert.pdf
[42]Norbert Wiener. Cybernetics, or Control and Communication in the Animal and the Machine, John Wiley & Sons, Inc., 1948.
[43]http://ieeecss.org/awards/ieee-css-hendrik-w-bode- lecture-prize
[44]黄一. 音容犹在——与韩老师的闲聊. 系统与控制纵横,2019, 6 (2): 24-30.
[45]N. Minorsky. Directional stability of automatically steered bodies. J Amer Soc.of Naval Engineers, 1922, 34: 280-309
[46]Tsien H S. Engineering Cybernetics. New York: McGraw-Hill, 1954.
[47]钱学森著,戴汝为、何善堉译. 工程控制论,科学
[48]黄琳. 《工程控制论》的意义. 控制理论与应用, 2014, 31(12).
[49]戴汝为. 从工程控制论到信息空间综合集成研讨体系. 上海理工大学学报,2011, 33(6).
[50]姜玉平. 钱学森与“工程控制论”的创立及其启示. 科学学研究,2006, 24(4).
[51]Murray R M, Astrom K J, Boyd S P, Brockett R W, Stein G. Future directions in control in an information-rich world, IEEE Control Systems Magazine, 2003, 23(2): 20-33.
[52]Guo L, Huang L, Jin Y H. Some recent advances of automatic control in China. Proceedings of 14th IFAC World Congress, 1999.