导语


1997年，计算机科学家 Wolfgang Maass 就提出，由脉冲神经元构成的网络——脉冲神经网络（SNN）会成为继人工神经网络后的“第三代神经网络模型”。作为神经科学和人工智能最前沿的交叉点之一，脉冲神经网络的研究从神经元节点的生物合理化出发，并有可能进一步整合类脑启发，突破现今人工神经网络在能量消耗、鲁棒稳定、连续学习等层面的瓶颈。在集智俱乐部「计算神经科学读书会」中，中科院自动化所博士生程翔从几个不同方面介绍了生物启发的脉冲神经网络设计的实例和思想。

研究领域：计算神经科学，类脑人工智能，脉冲神经网络，神经元模型，复杂网络
程翔 | 作者

目录

1. 神经元模型

2. 编码方式

3. 学习算法

4. 网络结构

5. 总结和展望



1997年，Wolfgang Maass于《Networks of spiking neurons: The third generation of neural network models》一文中提出，由脉冲神经元构成的网络——脉冲神经网络（SNN），能够展现出更强大的计算特性，会成为继人工神经网络后的“第三代神经网络模型”[6]。在SNN发展的早期，其训练过程更偏向于使用突触可塑性规则以追求生物合理性。但由于赫布学习和脉冲时序依赖可塑性等规则的局部权重优化特性，SNN 在计算特性上的优势没有被很好地发掘[12,13]。随着深度学习的复兴，SNN研究也更多地转向对性能的追求，ANN2SNN 的转换方法和基于代理梯度的反向传播方法日趋成熟。目前，在AI应用中，具有充足模拟时间的SNN已经能够获得与ANN相媲美的性能，这为SNN的进一步发展和神经形态硬件的研发提供了信心。

在这篇文章中，我想从四个方向对生物启发SNN设计的一些实例和思想进行介绍，包括神经元模型、编码方式、学习算法、网络结构，最后总结并展望类脑启发对于面向AI应用的SNN研究的意义。




1. 神经元模型




为了模拟生物神经元的活动模式，计算神经科学提出了一系列脉冲神经元模型。与使用激活函数的人工神经元相比，脉冲神经元普遍具有时序信息整合，阈上脉冲活动的特点。依照树突和轴突建模的空间复杂性，脉冲神经元可以分为单房室模型、缩减房室模型和详细房室模型。单房室模型中也存在着对可兴奋膜不同的建模方式，例如建模不同离子通透性的 Hodgkin-Huxley 模型和 Morris-Lecar 模型，基于非线性动力学分岔的 FitzHugh-Nagumo 模型和 Hindmarsh-Rose 模型，和基于固定阈值和复位机制的整合发放（integrate-and-fire）模型和振荡发放（resonate-and-fire）模型。

图1. 脉冲神经元的模型

由于计算复杂性的原因，大多数的脉冲神经元模型都不适用于类似人工神经网络的大规模模拟。Wolfgang Maass 在提出SNN时使用的是相对简单的整合发放模型，而带泄漏整合发放（leaky integrate-and-fire，LIF）模型[1]则是目前在面向AI的SNN研究中最为常用的脉冲神经元。一些面向SNN学习算法的工作将LIF神经元与循环神经元进行类比，这使得SNN能够更好地融入深度学习的框架之中。

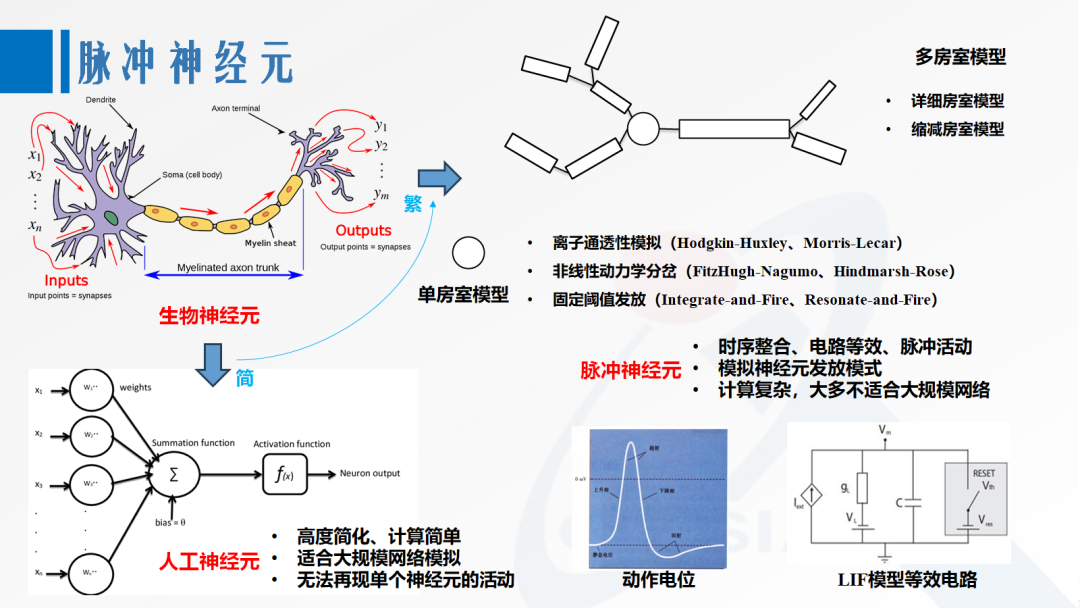
[1] Dayan P, Abbott L F. Theoretical neuroscience: computational and mathematical modeling of neural systems [M]. MIT press, 2005.

虽然LIF模型具有脉冲神经元的基本性质，但其一维线性动力学的膜电位整合过程也被认为“过于简单而不能产生皮层神经元一般丰富的发放模式”。一个常见的增强神经元动力学特性的方法，是引入自适应变量与膜电位形成一个二维系统，这种做法可以被解释为自适应的阈值变化或是内部的恢复变量。Izhikevich 神经元[2]在此基础上进一步将线性动力学替换为非线性动力学，并通过一组参数产生发放模式的异质性。该模型启发的相关工作表明，异质化的发放模式能够影响网络处理不同类型信息的能力，且混合网络能够在多类任务上同时获得性能优势。另一些实验表明，基于训练和初始化得到的时间常数异质性赋予SNN鲁棒性，使其能在广泛的环境中学习[3]。

[2] Izhikevich E M. Simple model of spiking neurons [J]. IEEE transactions on neural networks, 2003, 14(6): 1569-1572.
[3] Perez-Nieves N, Leung V C H, Dragotti P L, et al. Neural heterogeneity promotes robust learning[J]. Nature communications, 2021, 12(1): 5791.

图2. 神经元异质性




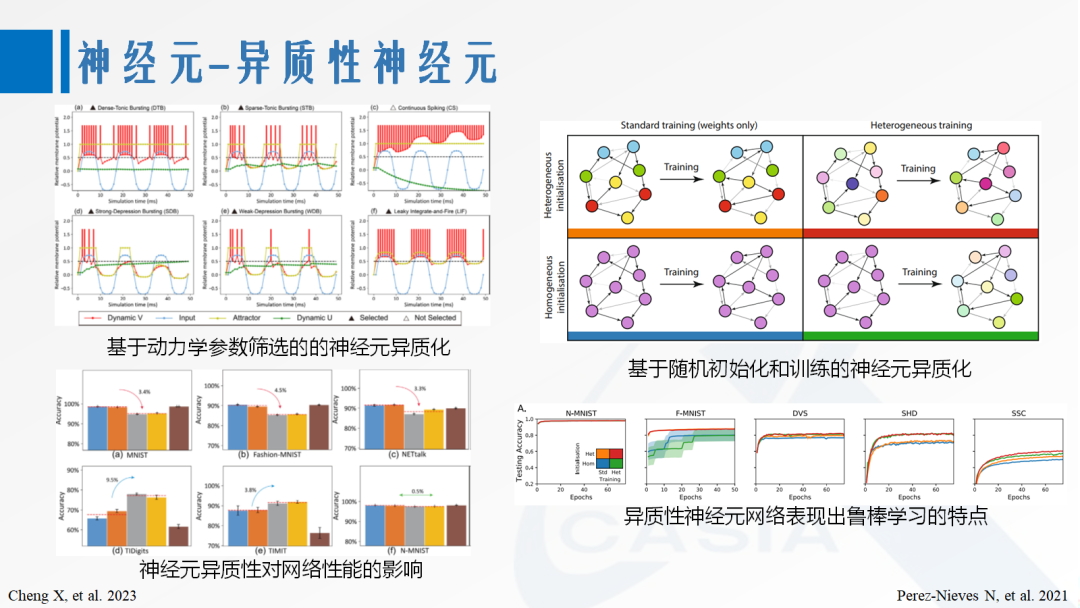
2. 编码方式




脉冲神经元的内在时序结构催生脉冲神经网络对非序列输入信息序列化的需求。根据生物神经系统对外界刺激的编码方式，许多能有效将信息存储到脉冲序列的编码方式被提出，包括频率编码（rate coding）、时序编码（temporal coding）、群体编码（population coding）、稀疏编码（sparse coding）和多种编码方式混合编码等。其中，利用离散时间内脉冲发放频率的频率编码最为常用，但是会忽略神经元放电时间与所编码信息间的联系[4]。时序编码能够利用脉冲发放时间，因而相较于频率编码更为精确，但也更为复杂，并且容易产生较高的推理延迟[5]。

[4] Adrian E D, Zotterman Y. The impulses produced by sensory nerve-endings: Part ii. the response of a single end-organ [J]. The Journal of physiology, 1926, 61(2): 151.
[5] VanRullen R, Guyonneau R, Thorpe S J. Spike times make sense [J]. Trends in neurosciences, 2005, 28(1): 1-4.

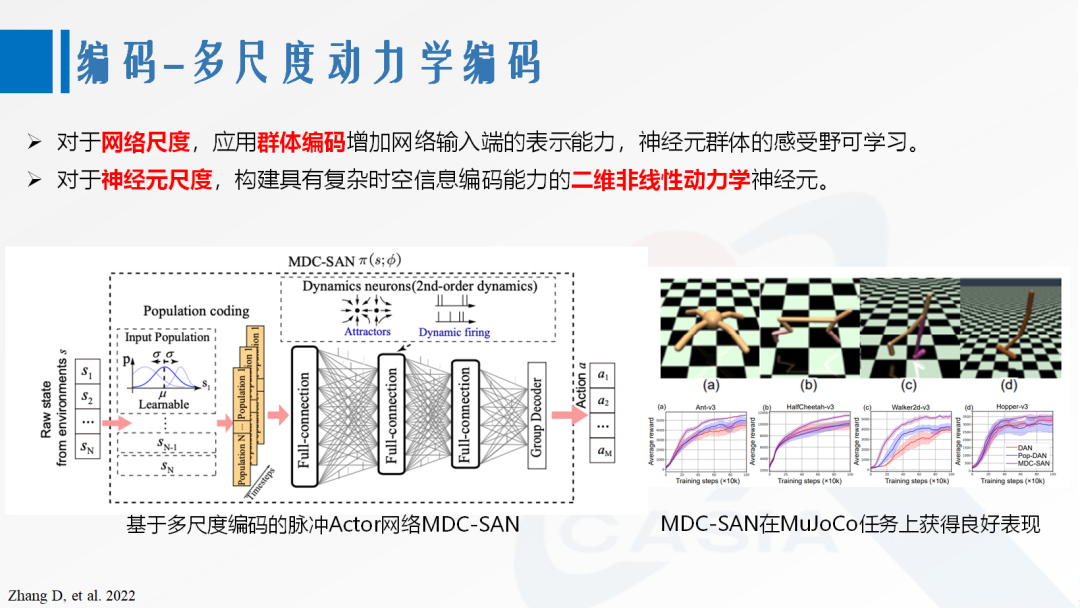
群体编码和稀疏编码考虑以多个神经元的共同活动来表征信息的场景。在群体编码中，每个神经元只对应一类信息的一部分特征，且可以同时对多类信息作出响应[6]。这种编码方式可以降低由异常活动带来的不稳定性，扩大信息表征空间，快速反应信息的变化。同时群体编码的复杂性较低，因而具有极大的应用潜力。在稀疏编码中，神经元群体中每个神经元只对一种特定信息作出响应且每种信息只激活少量神经元[7]。这种常在记忆相关的神经元群体中被发现的编码方式能减少信息间的干扰进而确保记忆的准确性。

图3. 多尺度动力学编码

[6] Pouget A, Dayan P, Zemel R. Information processing with population codes [J]. Nature reviews neuroscience, 2000, 1(2): 125-132.

[7] Olshausen B A, Field D J. Sparse coding of sensory inputs [J]. Current opinion in neurobiology, 2004, 14(4): 481-487.
[8] Zhang D, Zhang T, Jia S, et al. Multi-sacle dynamic coding improved spiking actor network for reinforcement learning[C]//Proceedings of the AAAI Conference on Artificial Intelligence. 2022, 36(1): 59-67.

在诸多编码方式的基础上，神经元以不同的编码方式传递不同类型的信息或在编码的不同阶段采用不同编码方式也是一类在神经科学实验中得到验证的现象[9]。这一现象体现了生物在处理信息时的灵活性，其在脉冲神经网络中的应用很可能是均衡提升网络性能、时延、能耗的关键。

[9] Panzeri S, Brunel N, Logothetis N K, et al. Sensory neural codes using multiplexed temporal scales [J]. Trends in neurosciences, 2010, 33(3): 111-120.





3. 学习算法




在脉冲神经网络领域发展的早期，学习算法的研究更侧重于对生物合理性的追求。许多神经科学提出的突触可塑性规则被用来指导学习算法设计，包括赫布理论[10]、长时程增强、长时程抑制以及脉冲时序依赖可塑性[11]等。这些规则是局部活动信息的整合，例如突触前后脉冲的相对时间或发放频率。虽然可塑性规则算法在生物合理性和计算复杂性上具有优势，但是由于难以利用全局指导信息，其性能始终落后于反向传播等先进人工神经网络学习算法。

[10] Do H. The organization of behavior [J]. New York, 1949.
[11] Markram H, Lübke J, Frotscher M, et al. Regulation of synaptic efficacy by coincidence of postsynaptic aps and epsps [J]. Science, 1997, 275(5297): 213-215.

随着近年来深度学习的兴起，脉冲神经网络研究对性能的需求愈发强烈。在该过程中，高性能人工神经网络向脉冲神经网络转化的技术日趋成熟[12]，放电过程不可微分这一使用反向传播算法训练脉冲神经网络的关键瓶颈也通过代理梯度的方式被解决[13]。这两种方法成为脉冲神经网络学习算法的主流。

[12] Cao Y, Chen Y, Khosla D. Spiking deep convolutional neural networks for energy-efficient object recognition [J]. International journal of computer vision, 2015, 113: 54-66.

[13] Wu Y, Deng L, Li G, et al. Spatio-temporal backpropagation for training high-performance spiking neural networks [J]. Frontiers in neuroscience, 2018, 12: 323875.


仍有一些工作尝试借鉴生物规则实现SNN的监督学习。其中，神经调制是一类常被关注的全局信息传播方式。三因子学习在突触前后神经元活动之外引入了神经调制的影响[14]。其中，局部可塑性通常以资格迹（eligibility trace）的形式累积，并在“奖励”延迟发放后作用于突触权重。另一种神经调制的建模方式是元可塑性，即将可塑性幅度和极性的变化建模为神经调质（neuromodulator）水平的函数进而实现高能效的全局信度分配[15]。

[14] Frémaux N, Gerstner W. Neuromodulated spike-timing-dependent plasticity, and theory of three-factor learning rules [J]. Frontiers in neural circuits, 2016, 9: 85.

[15] Zhang T, Cheng X, Jia S, et al. A brain-inspired algorithm that mitigates catastrophic forgetting of artificial and spiking neural networks with low computational cost[J]. Science Advances, 2023, 9(34): eadi2947.

一些从生物视角解释反向传播（BP）的过程中衍生出来的学习算法也被应用于SNN 和 ANN 的优化。BP通过计算权重变化和误差间的关系找到最优的梯度下降方向，其中涉及的独立反馈通路、精确误差计算、相干双向矩阵等都不一定能够在生物中找到物质基础。通过降低计算过程的精确性，可以建立BP与一些生物机制的对应关系：反馈对齐等一类学习算法解耦了双向矩阵间相干性[16]；NGRAD框架将学习分解为神经元活动误差和局部梯度的结合[17]；自组织反向传播算法建模了可塑性逆向传播的介观过程[18]；BP-STDP则证明了STDP和BP在特定情况下的等价性[19]。这些算法很难在准确性上实现对BP的大幅超越，但是却能够在保证准确性接近的情况下有效降低训练成本，而这二者间的折衷对于生物在真实世界中的生存具有相当的意义。

图4. 近似反向传播（BP）算法的发展

[16] Lillicrap T P, Cownden D, Tweed D B, et al. Random synaptic feedback weights support error backpropagation for deep learning [J]. Nature communications, 2016, 7(1): 13276.
[17] Lillicrap T P, Santoro A, Marris L, et al. Backpropagation and the brain [J]. Nature reviews neuroscience, 2020, 21(6): 335-346.
[18] Zhang T, Cheng X, Jia S, et al. Self-backpropagation of synaptic modifications elevates the efficiency of spiking and artificial neural networks[J]. Science advances, 2021, 7(43): eabh0146.
[19] Tavanaei A, Maida A. BP-STDP: Approximating backpropagation using spike timing dependent plasticity[J]. Neurocomputing, 2019, 330: 39-47.

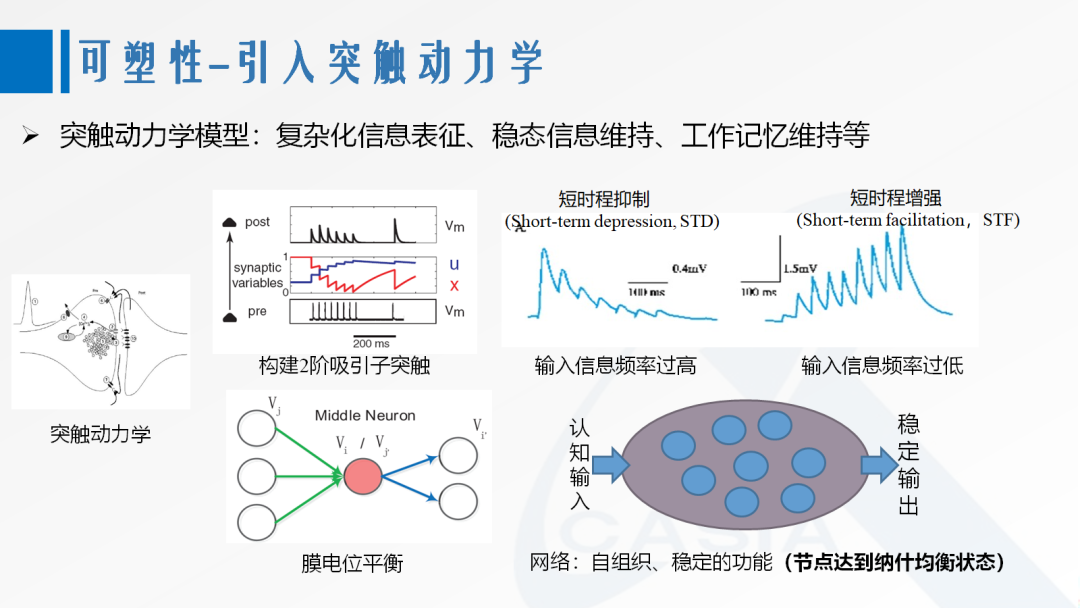
此外，还有一些短时程的突触可塑性机制在SNN中得到应用。与学习算法能够形成可固化到权重中的“知识”不同，短时程可塑性[20]对应动力学尺度，往往承担复杂化信息表征、稳态信息维持、工作记忆维持等微观功能。

图5. 突触动力学模型

[20] Stevens C F, Wang Y. Facilitation and depression at single central synapses [J]. Neuron, 1995, 14(4): 795-802.





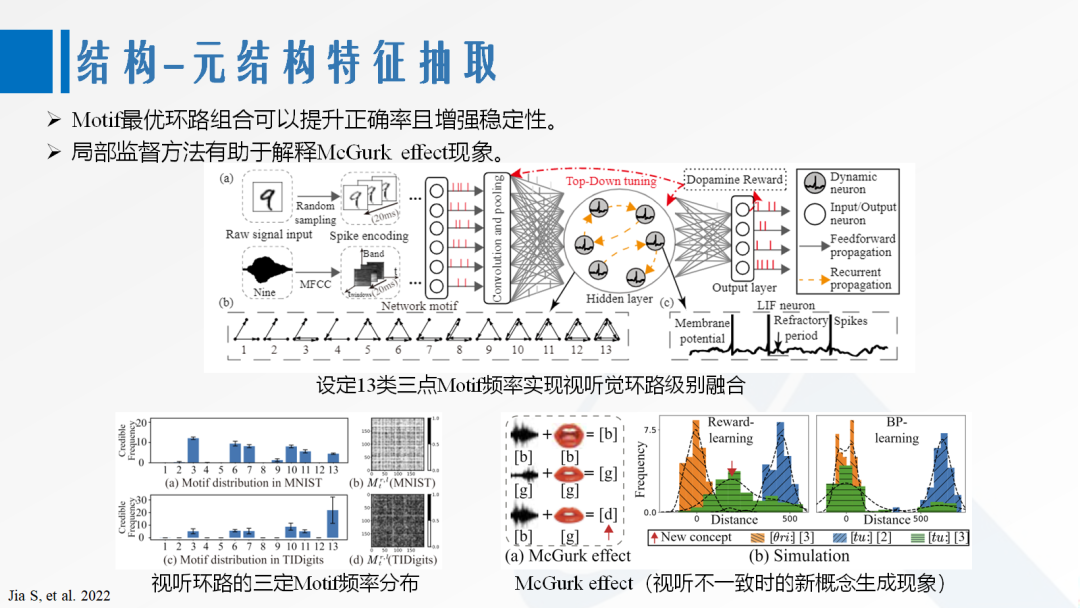
4. 网络结构




尽管经过长期的进化后的形成神经元连接方式对人工网络具有重要的参考价值。但目前，脉冲神经网络在结构设计上还是更多地依赖于人工神经网络中经典结构的复用，包括卷积结构、循环结构、残差结构等，生物的结构启发更多地聚焦于非全局尺度。由对马赫带现象的解释引发，在多种感知觉系统中得到验证的同层神经元间侧向交互作用是一种常被讨论的底层结构机制。在SNN研究中，这一机制常被用来形成winner-take-all网络或是增强特征并抑制噪声[21]。线虫神经系统中Tap-withdrawal反射受到特定环路控制。根据环路约束的稀疏网络可以实现高效的机器人控制[22]。

[21] Cheng X, Hao Y, Xu J, et al. LISNN: Improving spiking neural networks with lateral interactions for robust object recognition[C]//IJCAI. 2020: 1519-1525.

[22] Hasani R, Lechner M, Amini A, et al. A natural lottery ticket winner: Reinforcement learning with ordinary neural circuits[C]//International Conference on Machine Learning. PMLR, 2020: 4082-4093.

彩票假说中，一个大规模网络可以找到在与其功能上等价的小规模稀疏网络，这表明大规模网络中的功能性结构抽提是有理论可能性的。在此基础上，关键的结构特征和重要的拓扑环路经过调试后可以形成基础的结构算子。以Motif分布为例，Motif是指包含若干个神经元的环路单元，而不同类型Motif的占比即为Motif分布。基于不同分布可以形成前馈、反馈、循环等连接方式。多个生物系统都被发现符合特定Motif分布。基于三点Motif特征的相关工作可以实现环路级别的信息融合，在提升正确率的同时再现认知效应[23]。

[23] Zhang D, Zhang T, Jia S, et al. Multi-sacle dynamic coding improved spiking actor network for reinforcement learning[C]//Proceedings of the AAAI Conference on Artificial Intelligence. 2022, 36(1): 59-67.

图6. 元结构特征抽取

随着各国脑计划的立项和开展，全脑图谱的相关工作有望启发更具整体性的新型网络结构的设计。基于更多生物数据的支持，功能性结构抽提方法更有希望找到关键的连接模式。另一方面，由于脑是一个由多种功能各异的脑区组合成的“通用智能体”。因此，在利用图谱先验知识启发网络结构的过程中，一个可能的思路是先做减法，以脑区为单位形成特定功能的复现，再做加法获得近似脑的通用智能。

图7. 全脑图谱




5. 总结和展望




作为神经科学和人工智能最前沿的交叉点之一，SNN的研究从神经元节点的生物合理化出发，并有可能进一步的整合类脑启发，突破现今人工网络在能量消耗、鲁棒稳定、连续学习等层面的瓶颈。但在神经科学发展并不完善，脑高级功能和底层机理间存在黑盒的当下，单纯地从生物机制出发构建SNN很难得到和脑相同水平的复杂外显功能或是在深度网络的基础上取得巨大的性能突破，而从以功能复现为目标，数学化方法为手段的模式可能更适用于目前的类脑研究。但值得注意的是，类脑的神经网络研究同样也可以成为启发神经科学实验设计、解释相关实验结果、预估功能和机理间关系的一种手段。人工智能和神经科学的协同发展可能是二者去黑盒化并进一步发展的重要方式。


作者简介

程翔博士现就读于中科院自动化所，专业为模式识别与智能系统。研究方向主要包括脉冲神经网络、基于生物可塑性的学习算法、脑机接口算法，研究成果以第一作者发表在Science Advances、IJCAI、Neurocomputing、IEEE TNNLS等人工智能的顶级期刊和会议。


计算神经科学读书会


人类大脑是一个由数以百亿计的神经元相互连接所构成的复杂系统，被认为是「已知宇宙中最复杂的物体」。本着促进来自神经科学、系统科学、信息科学、物理学、数学以及计算机科学等不同领域，对脑科学、类脑智能与计算、人工智能感兴趣的学术工作者的交流与合作，集智俱乐部联合国内外多所知名高校的专家学者发起神经、认知、智能系列读书会第三季——「计算神经科学」读书会，涵盖复杂神经动力学、神经元建模与计算、跨尺度神经动力学、计算神经科学与AI的融合四大模块，并希望探讨计算神经科学对类脑智能和人工智能的启发。读书会从2024年2月22日开始，每周四19:00-21:00进行，持续时间预计10-15周，欢迎感兴趣的朋友报名参与，深入梳理相关文献、激发跨学科的学术火花！



详情请见：计算神经科学读书会启动：从复杂神经动力学到类脑人工智能



推荐阅读
1. 从复杂神经动力学到智能涌现：基于神经复杂性的类脑人工智能
2. 前沿综述：神经回路中的兴奋-抑制平衡、临界性与神经活动
3. 复杂性中何以涌现简单性？Sloppy模型捕捉复杂系统的关键自由度
4. 张江：第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程
5. 龙年大运起，学习正当时！解锁集智全站内容，开启新年学习计划
6. 加入集智，一起复杂！



点击“阅读原文”，报名读书会