1. 网络和相变
2. 生物系统中的信息转移
3. 总结
在前两篇文章中,我们介绍了为什么信息论方法在复杂系统研究中是重要的,并且我们已经有了一个研究框架,可以囊括所有的信息动力学,包括信息存储、信息转移和信息修正。尤其是在初等元胞自动机这样一个经典案例上,可以看到各种信息论指标如何揭示信息动力学。元胞自动机上的斑图是体现信息动力学的重要载体。静态的粒子(闪烁体)进行着信息存储,动态的粒子(滑行体)进行着信息转移,而粒子的碰撞则是在进行信息修正。如果读者对背后更多的数学细节感兴趣,可以参考第二篇文章《三种信息动力学:如何识别元胞自动机中的涌现?》。
在这一篇文章里,我们把目光从元胞自动机上移开,去看一看在更多样更复杂的系统里,信息动力学的相关指标是如何发挥作用的。
把模型建模成一个网络,主体看做节点,关系看作连边,这是我们研究复杂系统的重要手段。著名复杂科学学者米歇尔曾指出,一个重要的挑战是理解网络上信息传播的机制,以及这些网络是如何处理和加工信息的[1]。基于米歇尔的评论,也是区别于以往的研究,本文着重以信息存储、转移和修正的视角,对网络上的信息动力学建立一个定量化的理解框架。
接下来我们研究两个重要的网络模型,随机布尔网络(random boolean network,RBN)和电力网上的级联失效(cascading failures)。这两个网络都会经历一个相变的过程。所谓相变,指的是整个系统的状态随着关键参数的变化在无序和有序之间切换。随机布尔网络中这个关键参数是平均连接强度,而在级联失效中是网络的容错率。相变和信息动力学的联系来自于“混沌边缘”假设:一个处在临界相变状态附近的系统会展现出它最大的计算能力[2]。要注意,不只是混沌边缘处发生计算,在系统所有的相上都有不同程度的计算发生,这一点会在后续的实验结果中体现出来。
(1)随机布尔网络
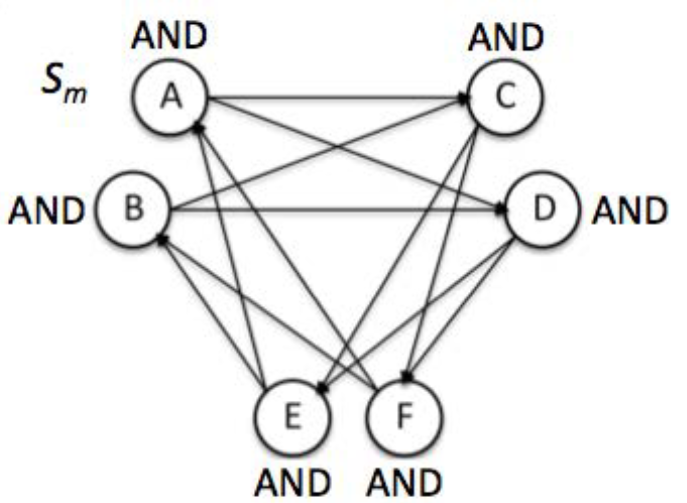
一个随机布尔网络由N个节点组成,每个节点取一个布尔值(0或者1),节点与节点之间的连接结构(邻接矩阵)是被随机确定的。我们可以让每个节点的入度恒定,或者给定一个已知平均入度的泊松分布。在节点更新上,每个节点根据邻居的状态,通过一个布尔函数计算出下一时刻的值。在经典的随机布尔网络中,所有节点是同时更新的。听起来是不是和元胞自动机很像?其实初等元胞自动机就是随机布尔网络的一个子类。
节点的活跃度可以用出现“1”的概率分布来衡量。如果概率接近0或1,说明整个网络非常稳定,活跃度较低。如果概率接近0.5,则活跃度较高。这个性质和相变有关。正如其他会发生临界相变的系统,我们也可以把整个随机布尔网络的状态分为有序相、无序相和临界区域。当网络平均度或者节点活跃度比较低时,系统处于有序相,会在宏观状态空间中非常强地收敛于某一个宏观态上。而如果平均度和活跃度比较高,则系统处于混沌的无序相。两个相之间有一个临界区域,在这个区域里系统处于“混沌的边缘”[2],有着非常高的关联长度。接下来我们来看看,为什么说在“混沌边缘”处系统展现出最大计算能力。
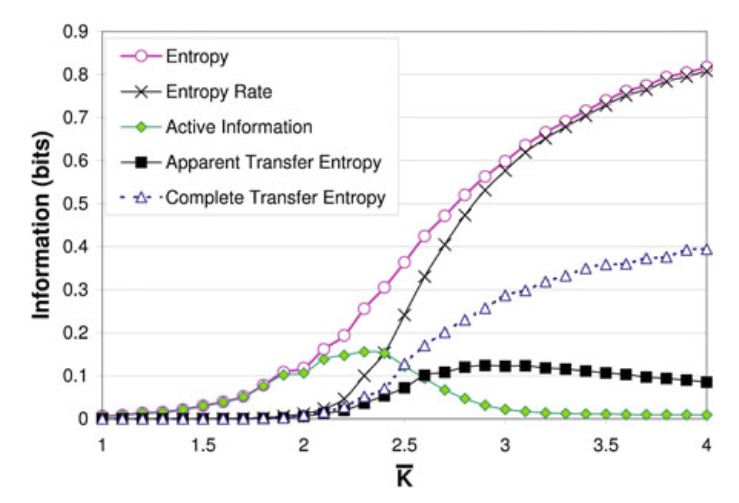
传统度量相变是否发生的方法是看它对初始条件的敏感度,或者某些影响在网络上传播的程度。这篇文章中,我们用信息动力学的指标来计算系统如何随着平均度变化而变化。在上一篇文章里,我们已经介绍了活跃信息存储(active information storage)、熵率(entropy rate)、转移熵(分为表面转移熵 apparent transfer entropy 和完全转移熵 complete transfer entropy)。在下图的实验中,计算的是对每个节点的平均值(总共250个节点),考虑到的历史长度为 k=14。
图中的结果告诉我们,有序相中占主导地位的是信息存储,即一个节点自身的历史主要决定了它自己的未来。而在混沌的无序相中,占据主导地位的是信息转移,也就是由邻居转递过来并不在节点历史里的信息。在相变区域,两者则达到了某种平衡。要注意的是,熵率也是一种特殊的转移熵,在确定的系统中等于整体的信息转移。另外,表面转移熵在进入无序相后开始下降,而完全转移熵一直在上升,说明在混沌的系统中,我们必须把所有的信息源都考虑进来,才能正确识别某一个信息源对目标产生的影响。
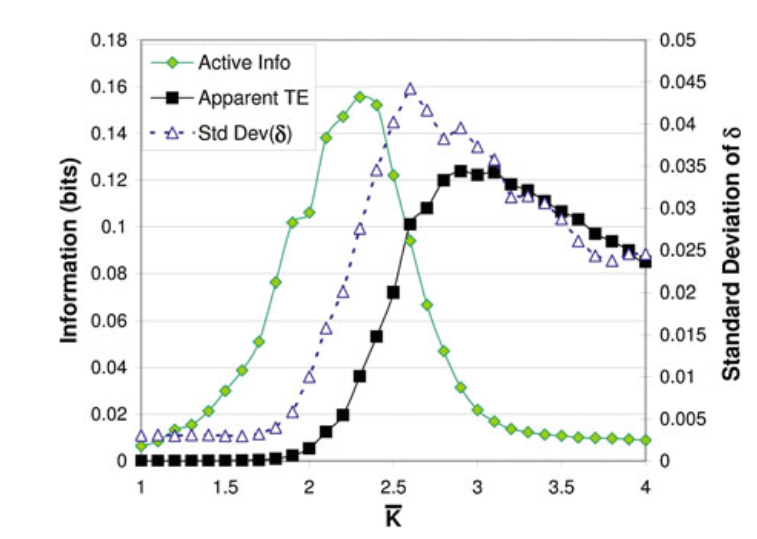
我们进一步把活跃信息存储和表面转移熵的峰值放在同一张图里比较。其中活跃信息存储峰值的出现更稍微倾向于有序相,而信息转移更倾向于无序相。下图中,δ是一个度量系统从相似的初始态出发,最终收敛或发散的程度,δ越高系统越倾向于发散。当系统发生相变时,一点微扰就会让系统发生巨大的改变,所以δ峰值的出现标志着临界相变的发生。它恰好出现在信息存储与信息转移相等的时候,进一步佐证了前文中所说的结论。
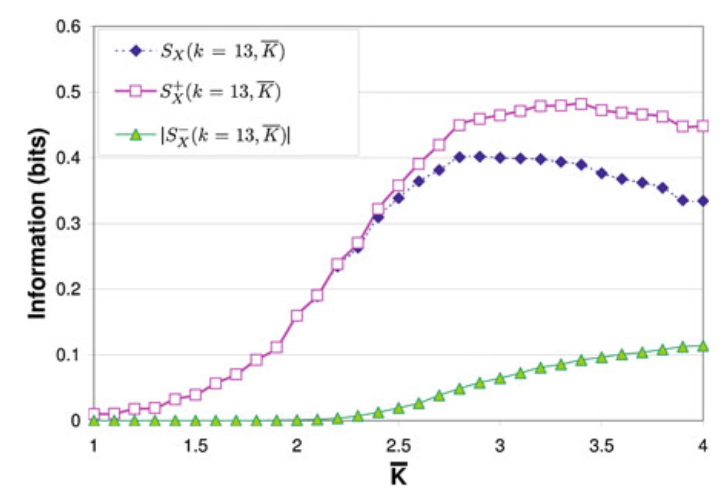
接下来看系统中信息修正的过程。对这一过程的一个主要度量指标是可分离信息S(separable information)。该指标大于0的部分表示的是平凡的信息修正,而小于0的部分则是非平凡的,对应元胞自动机里动态斑图的移动和碰撞。S在相变区域达到峰值,便是因为开始有越来越多的非平凡的信息修正。
最后需要指出的是,所有信息动力学指标的标准差在相变区域达到最大,说明随机布尔网络在相变时信息动力学的多样性达到了最大[3]。可惜参考文献中的图片不够清晰,这里没有展示,读者可自行查阅参考文献[3]。
(2)电力网上的级联失效
现代能源、通信、交通和金融网络都面临着级联故障事件的风险。级联故障是指局部故障触发雪崩机制,从而对整个网络产生巨大影响。我们的研究重点是能源网络,尤其是电力网络。在这些网络中,使用的增长速度超过了基础设施的投资(其中大部分已经接近其使用寿命的尽头),导致电网负载变得极为关键。因此,小的故障可能导致级联的灾难性停电,而且这类故障发生的频率越来越高,影响也越来越严重。这些故障可以中断重要服务,并造成数百万美元的损失。如果能理解其背后的机理,我们可以采取措施避免它们的发生。
我们依然可以使用网络来建模级联失效,其中每条边需要设定一个效率值(efficiency)eij(n),是该条边权重的倒数,在初始时刻初始化为1(如果边不存在则设为0)。随着时间,每条边的效率都可以更新。由此我们可以进一步定义最高效率路径的效率值εij(n)是从i节点到j节点的最短路径加权长度的倒数。另外设定每个节点有负载(load)Li(n)是经过该节点的最高效率路径的数量(和介数中心性(betweenness centrality)的概念是等价的)。每个节点还有另一个属性容量(capacity)Ci=α Li(0) ,表示的是节点在不崩坏的情况可以接纳的最大负载。一般如上式所示,我们用初始时刻每个节点的负载来决定它们的容量,其中α≥1是个给定的参数。
级联失效是如何发生的呢?当外来的攻击使得某个节点的负载超出其容量时,与它相连的连边效率会随之更新(相关数学细节可参看原文),于是其他节点之间的最高效路径会发生变化,进一步导致其他节点负载发生变化,于是会有更多的节点过载。可以想见,α越大,网络越不容易发生级联失效,而当α越小,甚至接近于1时,一点点微扰就会引发级联失效。它类似于前文随机布尔网络中的平均连接强度,较大时整个系统处于有序相,较小时则让系统处于无序相,中间会有相变的阶段。
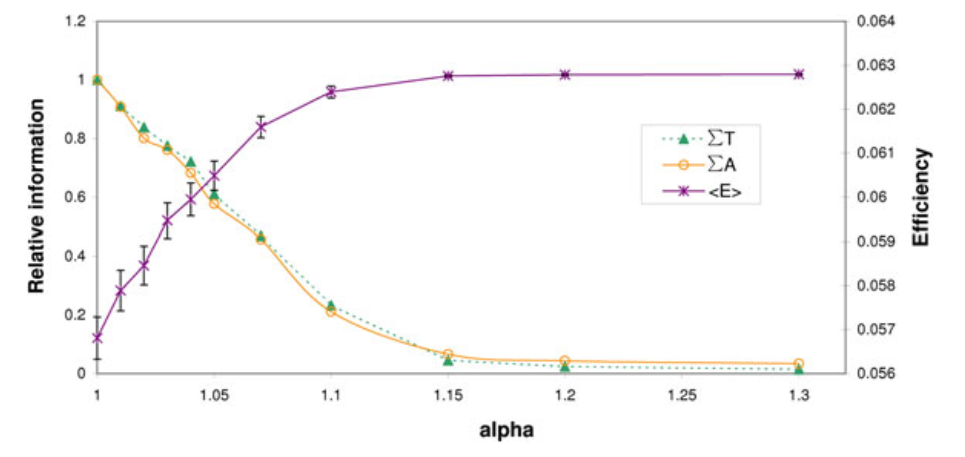
下图展示了实验结果,网络设定取自真实的数据,共有4941个节点,每次扰动是随机去除149个节点。在网络达到稳定后,测量其平均效率值(<E>)、平均表面转移熵(T)和平均活跃信息存储(A)。图中可以看到,在有序相的时候,信息存储是占据主导地位的,这和之前的结论一致。随着α降低,中间有一个相变区域,此时两类指标达到顶峰。进一步到无序相时,他们又开始微微下降。作者认为这也体现出混沌边缘处计算能力最大化的假说。
有意思的是,随着α降低,信息动力学指标先有一个急剧地上升(包括T和A),然后平均效率值再开始显著下降。不过这不意味着我们可以把它当作级联失效发生的早期指标(这不是时间上的先后顺序),而是意味着我们可以借此来检测网络是否处于临界负载状态(不能再削弱每个节点的容量了!)。
除此以外,作者也绘制了累积的(除了节点,也包括对时间的累积)局部信息转移和信息存储(两张图的纵轴都用了α=1时的数值进行了标准化处理)。和前面不同,总信息量会在有序相到无序相的过程中一直增加,这仅仅是因为级联失效过程中级联的长度更长。
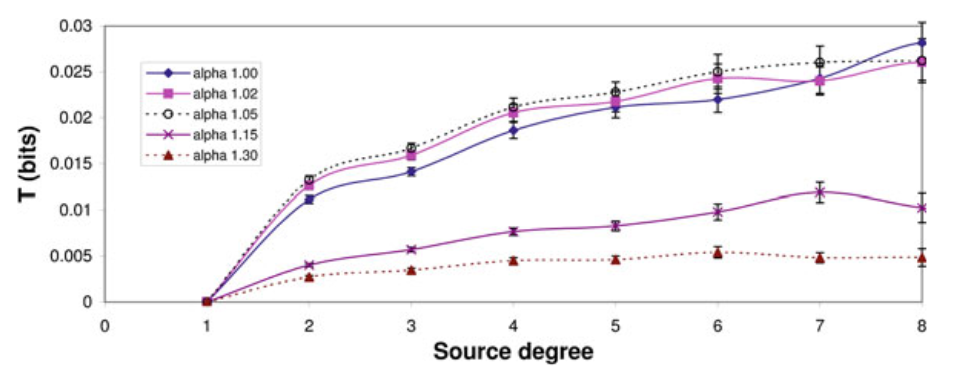
另外,既然这是在网络上进行的建模,那信息动力学指标和网络拓扑结构会不会有什么关联呢?下图展示了平均信息转移和节点度的强相关性。其中度为1时信息转移一定为0,因为它们没有介数中心性(除了它们自己作为起点或终点),所以它们的负载不会变的,也就没有信息转移或存储的能力。当一个节点有越来越多的邻居,它就有了更多信息源以及变化的多样性。同时,对于经过该节点的路径来说,更有可能传递让接受信息的节点更“惊奇”的信息。这都解释了为什么大度节点的出现可以增强一个网络的信息交换。事实上,大度节点连接的边平均比小度节点的连边能传递更多信息。这也印证了无标度网络会比随机网络“更好”地传播信息[4]。
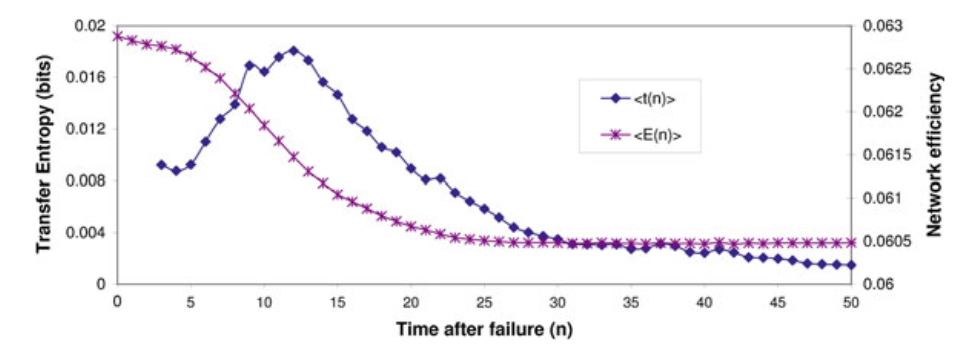
前面我们讨论的都是级联失效发生后,处于稳定状态的网络。接下来我们来看级联失效在时间上展开后,具体会发生什么现象。图中绘制了α=1.05的条件下,转移熵和效率值随时间的变化,α取其他值时变化趋势也是类似的。转移熵的峰值出现在初始故障发生后的大约12个时间步,虽然出现的较晚,但它可以在空间上指明级联失效发生的方向。转移熵的急剧上升和节点的负载情况并没有明显的关系,说明这是一种自组织涌现现象。它是在宏观层次上向我们揭示级联失效发生的规律。
总的来看,信息存储和信息转移分别在有序相和无序相中占据主导地位,而在相变发生时则达到平衡。它们可以用来识别网络上的相变,甚至可以作为某种指标让我们能够预测相变发生的情况(级联失效的方向)。它们和网络的拓扑结构也有很强的关系(随机布尔网络中的平均连接强度,级联失效中的节点度)。这些发现不止应用在网络上,也可以迁移到其它会发生相变的系统上[2,5]。在实际应用上,它们可以应用在生物网络[6]上,电力网上[7]以及金融市场中的级联失效效应[8]。
在前文中(包括之前的两篇推文),我们已经呈现出整个信息动力学的框架,并在一些例子上进行了应用(元胞自动机、RBN、级联失效等)。接下来我们要给大家看的是,这些理论如何帮助我们更好地理解一些有趣的生物系统。
(1)睡眠呼吸暂停中心率和呼吸速率的交互
睡眠呼吸暂停(sleep apnea)是睡眠过程中无规律地呼吸突然暂停或爆发。有学者用转移熵的方法来研究该现象,发现心率和呼吸速率之间似乎存在着双向的信息传递[10],表明这里有复杂的交互作用。
本文中采取局部转移熵来研究该交互作用。相比于计算平均值,局部指标能告诉我们更多两个变量在时间上交互的信息。实验采取了圣塔菲研究所1991年时间序列竞赛的B数据集第2350-3550个样本点[11]。在具体计算上,作者采取核估计法来估计概率分布。
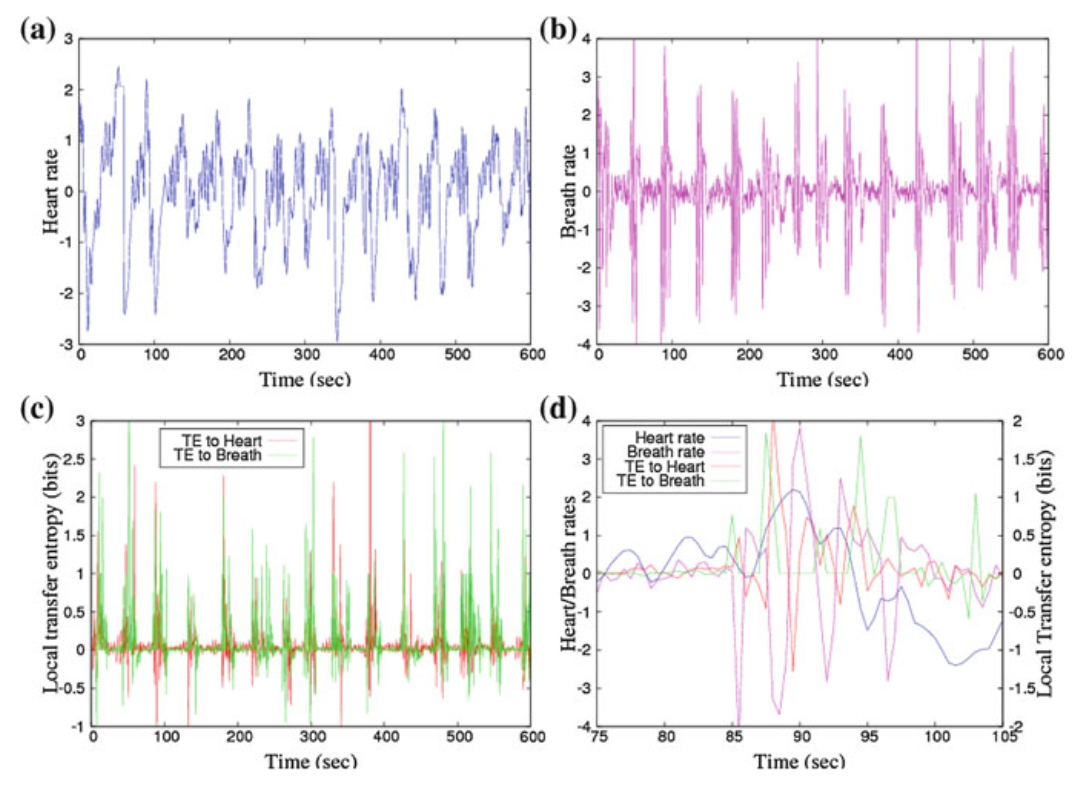
如下图所示,(a)中是心率变化曲线,(b)中是呼吸速率变化曲线。展示的数据都经过了标准化处理。(c)中展示了两个方向上的局部转移熵,当呼吸暂停事件发生时,两个局部转移熵都有剧烈的变化,而在事件发生之间则有较少的信息转移。(d)展示了一次呼吸暂停事件发生时,几条曲线的变化。我们发现,从心率到呼吸速率的信息转移最先显著上升(绿线的第一个尖峰),紧接着就开始了复杂的双向信息交换。心脏对呼吸的因果作用或许就是这种现象的源头。这种时间上的先后顺序应当比平均值的大小更能揭示谁在信息交换过程中占据主导地位。
(2)大脑上的信息结构
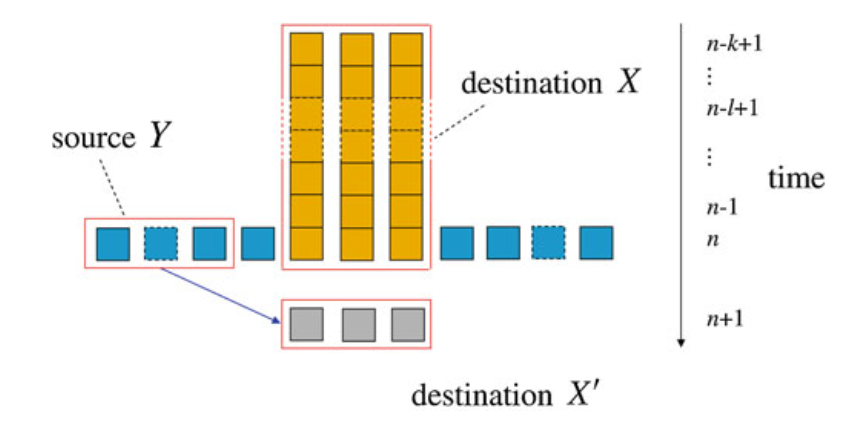
人脑上有着复杂而精细的信息处理和交互过程,尤其是各个脑区之间。首先,为了能更好地研究大脑上的信息动力学,我们需要先将之前的单变量转移熵拓展成多元变量的转移熵,如下图所示。这是因为我们想要度量脑区之间的转移熵,而每个脑区都有很多神经元节点,每一个节点都可以被视作一个变量,所以这是多元变量之间的信息转移问题。读者不妨用该图与《三种信息动力学:如何识别元胞自动机中的涌现?》中的转移熵图示进行比对,以此来更好地理解定量指标的变化。
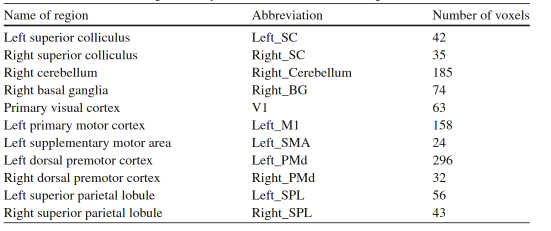
我们要用这个指标来度量大脑核磁共振(functional Magnetic Resonance Imaging, fMRI)数据里的信息动力学,数据背景是一次视觉追踪的任务。任务涉及8名志愿者,被要求用右食指追踪计算机屏幕上一个沿着圆形轨迹运动的视觉目标。这项任务需要整合来自视觉输入、运动规划和视觉及运动控制区域的信息,而且任务难度是可调的。此次实验研究的脑区对象共有11个,如下面的图表所示。
上图是用转移熵建立起来的脑区间的信息结构,可以大致分为三层。最顶层是负责规划和预期的区域,中间层是视觉感知处理的区域,最底层是行动决策的区域。连边的宽度体现的是影响的显著性。这个层次结构和实验结果有很好的对应。如果我们已知上层结构的状态,可以用来预测下层结构的变化。但是,从视觉感知区域到行动决策区域的反馈链接并未明显出现。这可能是因为这些反馈链接的操作时间尺度比这里的fMRI测量要短(间隔超过2秒)。也就是说,关于物体位置的原始视觉信息可能在很短的时间内(即在两秒内)对行动决策区域的活性产生影响。
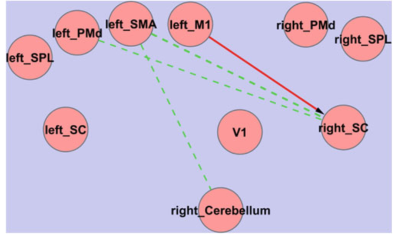
上图是在任务难度变化时,互信息和转移熵与任务难度之间的相关性。三条绿色虚线表示这三对区域之间的互信息与任务难度呈正相关,红色实线表示它们之间的转移熵与任务难度呈负相关关系。这个结果清晰地展现出,任务难度的增加有助于加强运动规划区域(leftPMd、leftSMA)和决策区域的联系。其中right_SC负责眼球的移动,rightCerebellum负责手部的运动。
在未来,随着测量手段的进步, 我们可以计算更加细微时间尺度上的信息转移,或许可以有更多惊奇的发现。
(3)连贯信息结构的进化
连贯信息结构(coherent information structure)指的是复杂系统计算中会被持续观察到的一个特征。这个概念的提出是想指代各个系统中类似于元胞自动机中滑翔体(glider)那样的结构,比如鸟群的集群行为,基因网络上的信号传播还有神经元集群中的“波”等等。关于这个术语进一步详细的讨论,读者可以参见文献[9]。要注意的是,这里的连贯性是在信息的意义上讲的,像某些粒子,直观上可能并不连贯,看起来有些跳跃,但它们在时空坐标相近时,局部信息转移会有相似且连贯的取值。
根据朗顿的分析[2],混沌边缘处系统会有最大的计算能力,这一点如何从连贯信息结构的角度分析?作者认为,相比于处于混沌边缘的系统:过于有序的系统虽然有连贯信息结构,但结构太小;而过于混沌的系统,任何结构的连贯性都被破坏了。
在这个小节里,作者使用转移熵作为适应度函数来设计一个进化任务,想要检验信息转移是否就是生物体协同运动的基础,以及当一个系统最大化信息转移的时候,会产生何种涌现行为。在实验中,作者确实发现了连贯信息结构,类似于滑翔体,对于系统的计算来说,是非常有用的结构。
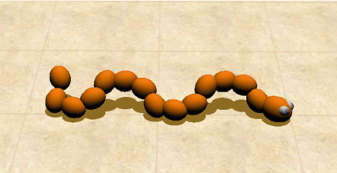
实验对象是一个蛇形机器人,如下图所示。它由一系列的球状物关节组成,每个关节可以在水平方向和垂直方向上各有一个旋转角度。适应度计算的是,平均每个关节的表面转移熵,方向是从尾部到头部。计算转移熵使用的数据是实际转角的时间序列数据。进化时,作者使用遗传算法(genetic programming, GP)迭代200个蛇形机器人,每次筛选出适应度函最高的子代[12]。
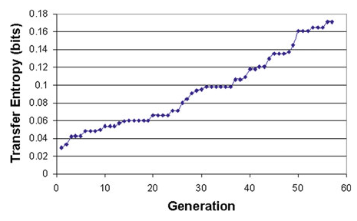
随着迭代次数增加,下图展示出每一代中适应度最高的个体的转移熵变化曲线。我们可以对比最终转移熵较高的个体(第57代,0.175bits)和转移熵较低个体(0.007bits)在行为上有什么区别。实验发现,低转移熵个体可以表现出快速且协调的持续行为。这是因为相比于关节间信息转移,和关节自身记忆的联系对协调行为更加重要。这就像是找到了一个吸引子,每个关节只需重复自身的历史就可以达成一个协调的状态。
而转移熵最高的个体展现出的是一种复杂的蠕动行为,如下面的动图所示。
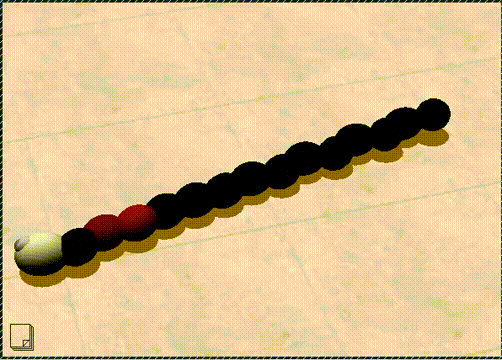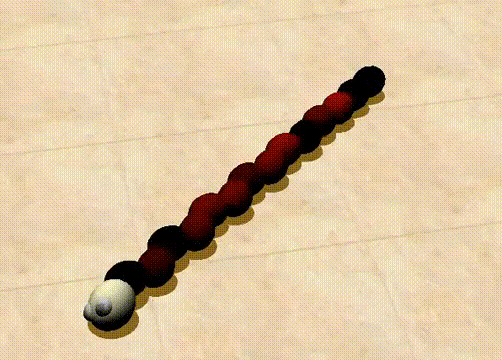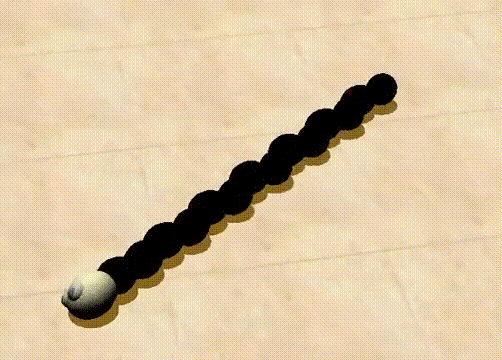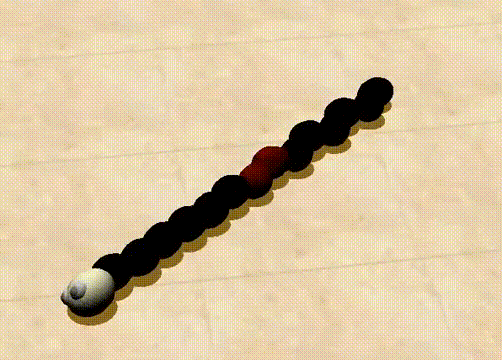
https://youtu.be/n31GsuS_oSM
这种动力学可以通过转向角的度量反映出来。下图(a)表示了13个关节的水平转向角变化,灰黑色是正值,黄色到红色是负值,纵轴是时间演变。图(b)展示了对应转移熵的大小,因为负值非常少,这里就只展示了正值。局部转移熵的变化告诉我们,这里有一个连贯信息结构从尾部移动到头部。体现在图(b)中,每次出现连贯信息结构,正的局部转移熵先出现在尾部关节,然后“移动”到头部关节。
为了更清晰地展现出如上所述的过程,我们再看下面的动图。图中黑色代表零局部转移熵,红色代表正局部转移熵。

https://youtu.be/HmRI5hfaBQ8
连贯信息结构的转移正是从尾部到头部,如下图(a)→(b)→(c)。
观察局部转移熵的大小变化情况,不难发现这里有不同种类的连贯信息结构。有的移动快,有的移动慢,有的包含信息量多,有的包含信息量少,正如元胞自动机中也有五花八门的滑翔体。这些结构正是复杂系统实现最大计算能力的要素。整个实验同时还告诉我们,以每条连边转移熵最大化为目标,在某种程度上正契合复杂适应系统的进化机制。虽然拥有最大转移熵的蛇形机器人不会快速而协调的运动,但它们有足够的计算能力,使得它们在充满挑战的环境中找到正确的方位。
总结一下,我们把局部转移熵应用在了生物学系统上(蛇形机器人也算是一种仿生系统),发现局部转移熵相比于以往计算平均值来说可以揭示更多有意思的洞见。目前已有的实验对象包括睡眠呼吸暂停、大脑中的层次结构以及蛇形机器人的进化,足可见复杂系统中的信息动力学的应用普适性。未来我们可以延展这个领域,洞察更多复杂系统的本质。
至此,这个小系列总共三篇文章完结了。在第一篇文章中,我们介绍了用信息论研究复杂系统的缘起,尤其是朗顿的混沌边缘假说,让学者们关注到了复杂系统本身的组织形式及其内在的计算能力,而不是只停留在某个复杂系统的物质机理上;第二篇文章呈现了一个理论量化框架,包括信息存储、信息转移和信息修正这三类信息动力学的度量,并在初等元胞自动机上详细分析比较了各种量化指标的性质和作用,有较多的数学细节;在这第三篇文章,我们将目光重新聚焦在一个个更为实际的复杂系统和研究问题上,应用信息动力学量化指标解决网络相变以及生物学相关的各类问题。
回到解读Lizier这篇博士论文的初心,它并非一块孤立的研究领域,而是与我们之前在因果涌现读书会中解读过的整合信息分解理论有着血脉相连的关系。所以我们可以把这篇博士论文当作一个前传,放置在一个更大的研究框架下去理解。
以下是给读者推荐的一个集智公众号文章的学习路径,帮助大家用信息论的工具洞悉复杂系统本质:
以后我们还将关注更多与该脉络相关的新研究,丰富这一条学习和研究路径。
参考文献
[1] M. Mitchell, Complex systems: network thinking. Artif. Intell. 170(18), 1194–1212 (2006)
[2] C.G. Langton, Computation at the edge of chaos: phase transitions and emergent computation. Phys. D 42(1–3), 12–37 (1990)
[3] C. Gershenson, Phase transitions in random Boolean networks with different updating schemes. arXiv:nlin/0311008v1 (2004), http://arxiv.org/abs/nlin/0311008
[4] E. Estrada, Information mobility in complex networks. Phys. Rev. E 80(2), 026104 (2009)
[5] O. Miramontes, Order-disorder transitions in the behavior of ant societies. Complexity 1(3), 56–60 (1995)
[6] M. Aldana, Boolean dynamics of networks with scale-free topology. Physica D 185(1), 45–66 (2003)
[7] S. Abu-Sharkh, R.J. Arnold, J. Kohler, R. Li, T. Markvart, J.N. Ross, K. Steemers, P. Wilson, R. Yao, Can microgrids make a major contribution to UK energy supply? Renew. Sustain. Energy Rev. 10(2), 78–127 (2006)
[8] F. Schweitzer, G. Fagiolo, D. Sornette, F. Vega-Redondo, A. Vespignani, D.R. White, Economic networks: The new challenges. Science 325(5939), 422–425 (2009)
[9] C.R. Shalizi, R. Haslinger, J.-B. Rouquier, K.L. Klinkner, C. Moore, Automatic filters for the detection of coherent structure in spatiotemporal systems. Phys. Rev. E 73(3), 036104 (2006)
[10] T. Schreiber, Measuring information transfer. Phys. Rev. Lett. 85(2), 461–464 (2000)
[11] D.R. Rigney, A.L. Goldberger, W. Ocasio, Y. Ichimaru, G.B. Moody, R. Mark, in Multi-channel physiological data: description and analysis, ed. by A.S. Weigend, N.A. Gershenfeld. Time Series Prediction: forecasting the future and understanding the past (Addison-Wesley, Reading, 1993), pp. 105–129
[12] I. Tanev, T. Ray, A. Buller, Automated evolutionary design, robustness, and adaptation of sidewinding locomotion of a simulated snake-like robot. IEEE Trans. Robot. 21(4), 632–645 (2005)
跨尺度、跨层次的涌现是复杂系统研究的关键问题,生命起源和意识起源这两座仰之弥高的大山是其代表。从2021年夏天至今,集智俱乐部已经陆续举办了四季「因果涌现」读书会,系统梳理了因果涌现理论的发展脉络,深入探讨了信息整合与信息分解的本质,并探索了在生物网络、脑网络、机器学习等跨学科领域的应用。此次因果涌现读书会第五季将追踪因果涌现领域的前沿进展,展示集智社区成员的原创性工作,希望探讨因果涌现理论、复杂系统的低秩表示理论、本征微观态理论之间的相通之处,对复杂系统的涌现现象有更深刻的理解。读书会从2024年4月19日开始,每周五晚20:00-22:00进行,持续时间预计8-10周。欢迎感兴趣的朋友报名参与!