写给物理学家的生成模型

导语
1. 引言
1. 引言
费曼在他的黑板上留下一句话:“what I can not create,I do not understand”[1]。三十年后,这句话被如今大红大紫的OpenAI当作信条挂在网站上[2]。确实,无论是在物理学还是人工智能的研究中,有能力创造往往才意味着最高层次的理解。
什么是创造?生成式人工智能 (Generative AI) 对此的回答是:学习数据样本背后的概率分布,并通过随机采样生成新的样本。这两年,人们用人工智能产品创造了无数令人惊艳的画作、引人入胜的故事、动人心弦的音乐。当然,还有广告文案、新闻报道、审稿报告、商业计划书、推荐信等等 (例如这句话本身)。人工智能创造的源泉是数据本身,而人工智能创造的引擎则是“生成模型”:一种用于表达、学习和采样数据背后的概率分布的人工神经网络。生成模型和统计物理的关系非常紧密。一旦了解生成模型的物理学基因,就比较容易理解和改造它们,甚至发明新的生成模型。本文从物理学的角度介绍几类常见的生成模型,并举例说明它们在科学研究中的应用。
相对于性质预测之类的“判别式”任务,“生成式”人工智能更难、更基础、也更有用。用数学语言描述,性质预测的目的是拟合函数y=f(x)。这里x是神经网络的输入,通常是代表微观结构的高维变量。y是输出,通常是代表宏观性质的低维变量。在性质预测之外,人们往往还更关心从宏观性质到微观结构的反向设计问题。由于从结构到性质的函数不可逆,简单地寻找它的反函数往往不能成功。概率建模提供了一个有用的视角。这时,性质预测就是要学习条件概率分布p(y|x)。而反向设计意味着给定宏观性质y,从条件概率p(x|y)中采样生成新的微观构型x。贝叶斯公式告诉我们p(x|y)∝p(x)p(y|x)。可见,把握微观构型的概率分布p(x)是“生成式”任务区别于“判别式”任务的关键。
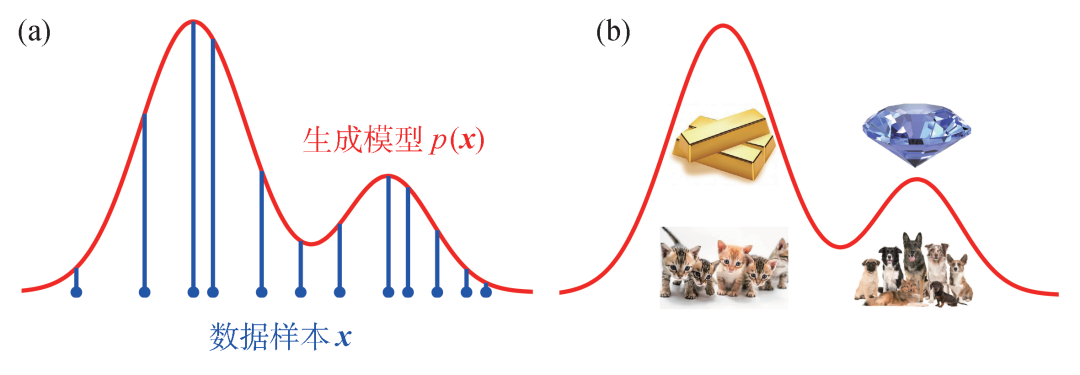
图1形象地展示了生成模型在做什么。图1(a)中的蓝色点代表数据样本,生成模型需要学会数据背后的概率分布,并据此生成新的样本。生成模型能够处理的数据类型无所不包。如图1(b)所示,图像生成模型表达了像素取值的概率分布,而材料生成模型表达了原子类型和坐标的联合概率分布。可以想象,无论是所有像素取值所构成的图像空间,还是所有原子种类和排布所构成的材料空间,都巨大无比。而人们真正关注的自然图片和稳定材料,仅仅占据这些空间中一个小角落。生成模型需要尽量提取数据样本中的统计规律,才能生成浑然天成的新图片和新材料。
2. 自然界中的概率分布
2. 自然界中的概率分布
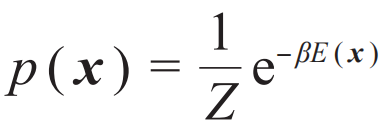 ,其中E(x)是伊辛构型x的能量,配分函数Z是概率分布的归一化因子。不同的温度1/β会导致不同的玻尔兹曼分布,甚至给出截然不同的磁化强度、比热等宏观物理量。
,其中E(x)是伊辛构型x的能量,配分函数Z是概率分布的归一化因子。不同的温度1/β会导致不同的玻尔兹曼分布,甚至给出截然不同的磁化强度、比热等宏观物理量。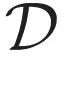 。这里所谓“模型”是指给定参数θ预测数据的条件概率p(
。这里所谓“模型”是指给定参数θ预测数据的条件概率p(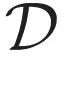 |θ),而所谓“推断”就是要确定如何根据观测数据选取模型参数。贝叶斯推断考虑对于给定的数据和参数的先验概率分布p(θ),从“后验概率”
|θ),而所谓“推断”就是要确定如何根据观测数据选取模型参数。贝叶斯推断考虑对于给定的数据和参数的先验概率分布p(θ),从“后验概率”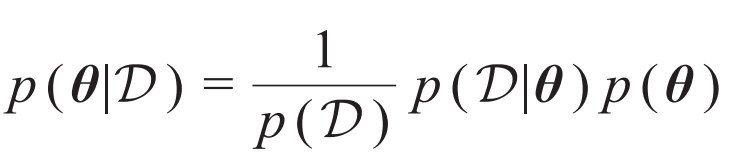 中选择参数。稍微改写一下后验概率的表达式,可以看到贝叶斯推断和统计物理之间的对应关系,见表1。其中,后验概率的归一化因子p(
中选择参数。稍微改写一下后验概率的表达式,可以看到贝叶斯推断和统计物理之间的对应关系,见表1。其中,后验概率的归一化因子p(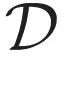 )对应于配分函数Z,在贝叶斯推断中被称为边际似然,它描述了模型对数据的总体刻画能力。
)对应于配分函数Z,在贝叶斯推断中被称为边际似然,它描述了模型对数据的总体刻画能力。
BOX 1
相对熵是信息论的一个基本量,也被称为Kullback—Leibler散度。它度量了概率分布之间的相似度。对于两个归一化的概率分布q和p,相对熵总是非负的[3]:
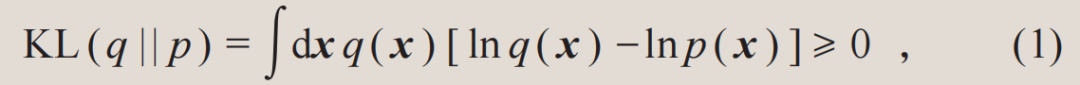
其中等号仅在两个概率分布相等时取到。因此,相对熵常常被用作训练生成模型的目标函数。通过最小化生成模型所表达的概率分布和目标概率分布之间的相对熵,可以让生成模型学会目标概率分布。
为什么要选择相对熵这个看起来奇怪的度量,而不直接使用类似于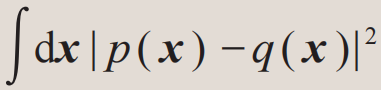 这样的均方差度量?主要有两个原因:第一,概率分布p(x)和q(x)在数量级上可能差别巨大,均方差距离不能充分体现这点差别,而相对熵中比较概率函数的对数可以更好地处理这种数量级差异;第二,其实不值得在两个概率分布都取值极其小的区域比较它们的差异,因此,相对熵的定义中按照概率q(x)加权计算,即集中检查对于概率q(x)而言有意义的空间中两个概率分布对数的差别。
这样的均方差度量?主要有两个原因:第一,概率分布p(x)和q(x)在数量级上可能差别巨大,均方差距离不能充分体现这点差别,而相对熵中比较概率函数的对数可以更好地处理这种数量级差异;第二,其实不值得在两个概率分布都取值极其小的区域比较它们的差异,因此,相对熵的定义中按照概率q(x)加权计算,即集中检查对于概率q(x)而言有意义的空间中两个概率分布对数的差别。
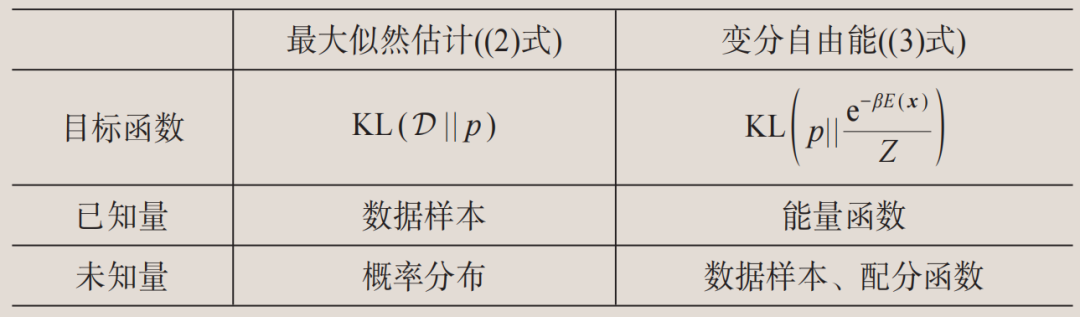
从定义(1)可见,相对熵对于概率分布q和p的互换并不是对称的。相对熵的AB面刚好对应了生成模型在数据建模和理论计算中的两种应用,见下表。首先,最小化数据集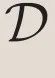 所代表的经验概率分布和模型分布之间的相对熵,等价于最小化以下的目标函数:
所代表的经验概率分布和模型分布之间的相对熵,等价于最小化以下的目标函数:
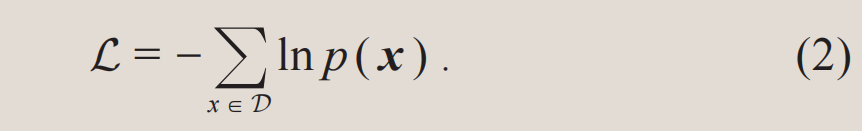
因为ln p(x)在统计学中被称为对数似然函数,最小化(2)式也被称为最大似然估计(maximum likelihood estimation)。注意,训练数据仅仅是目标概率分布中有代表性的样本,而不是目标分布本身。因此,过分地优化(2)式会导致过拟合现象。以图1(a)为例,如果模型学到的概率分布仅仅在蓝色数据点上非零,它就只会死记硬背训练数据,而不能再生成新的样本。
其次,在统计物理研究中人们往往知道体系的能量函数E(x),而需要得到的是服从玻尔兹曼分布的样本x以及配分函数Z。这种场景和数据驱动的最大似然估计恰恰相反。此时,可以将模型分布p(x)当作变分概率分布,并最小化它和物理系统的玻尔兹曼分布之间的相对熵。这等价于变分自由能:
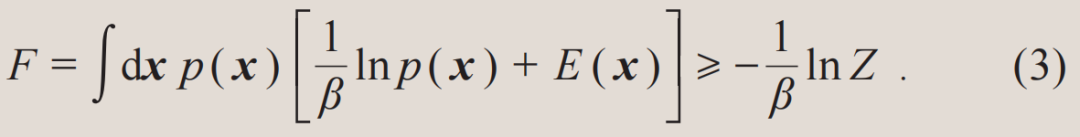
其中不等号来自于相对熵的非负性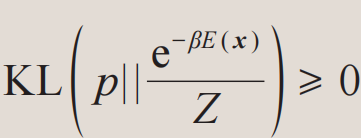 。(3)式中两项的物理含义分别是变分概率分布的熵和能量期望值。当不等式取等号时,变分概率分布等于真实的玻尔兹曼分布,变分自由能计算也就严格地解决了问题。注意到变分计算并不依赖于事先准备好的训练样本,因为样本可以从生成模型概率分布p(x)中采样得来。此外,变分计算也不需要担心过拟合,变分自由能这个目标函数值越低越好。
。(3)式中两项的物理含义分别是变分概率分布的熵和能量期望值。当不等式取等号时,变分概率分布等于真实的玻尔兹曼分布,变分自由能计算也就严格地解决了问题。注意到变分计算并不依赖于事先准备好的训练样本,因为样本可以从生成模型概率分布p(x)中采样得来。此外,变分计算也不需要担心过拟合,变分自由能这个目标函数值越低越好。
生成模型的最大似然估计和变分自由能计算是同一枚硬币的两面
3. 生成模型速览
3. 生成模型速览
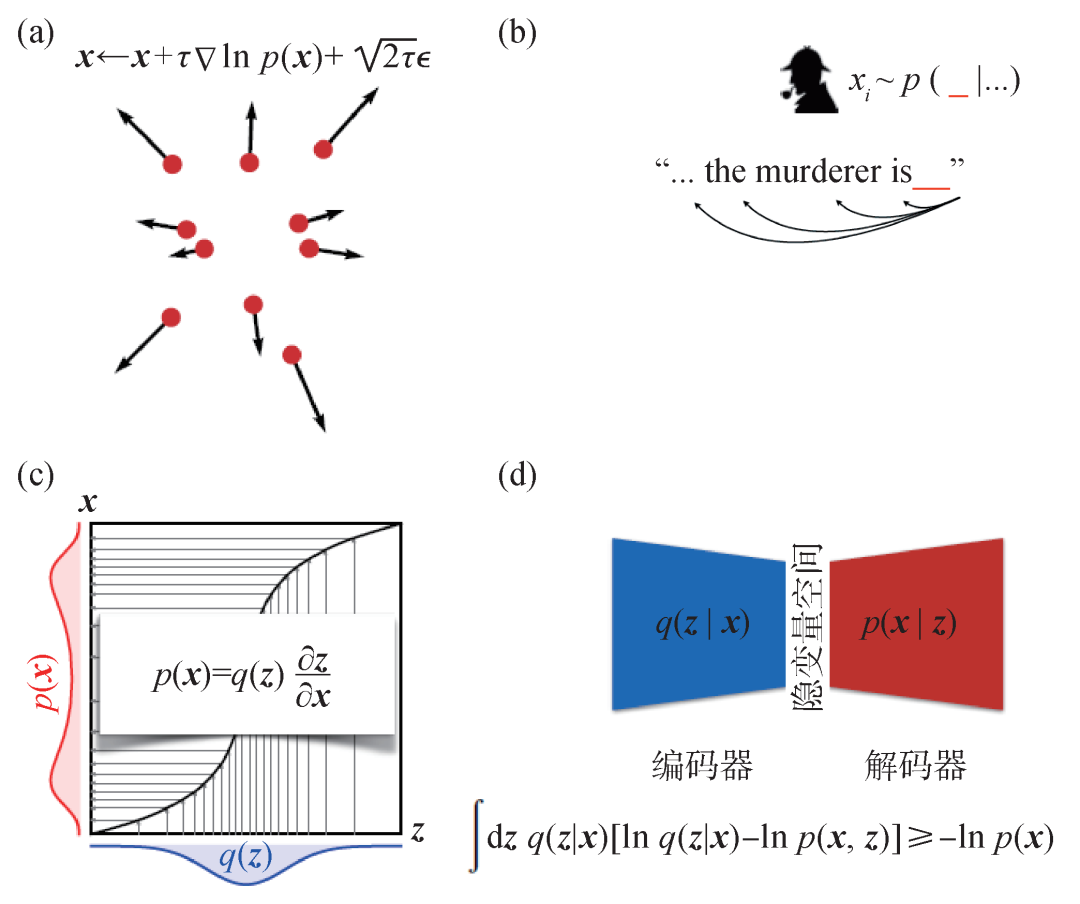 图2 四类生成模型和它们背后关键的数学公式 (a)扩散模型:朗之万方程;(b)自回归模型:条件概率分解;(c)流模型:变量替换;(d)变分自编码器:变分贝叶斯推断
图2 四类生成模型和它们背后关键的数学公式 (a)扩散模型:朗之万方程;(b)自回归模型:条件概率分解;(c)流模型:变量替换;(d)变分自编码器:变分贝叶斯推断
3.1 玻尔兹曼机和扩散模型
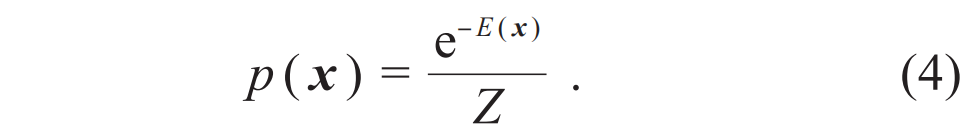
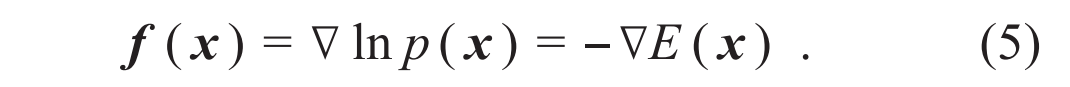
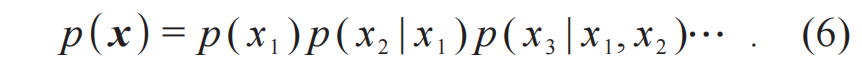

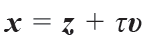 ,再考虑τ→0的连续时间极限,可以得到一个关于含时概率密度的连续性方程[26,27]:
,再考虑τ→0的连续时间极限,可以得到一个关于含时概率密度的连续性方程[26,27]:
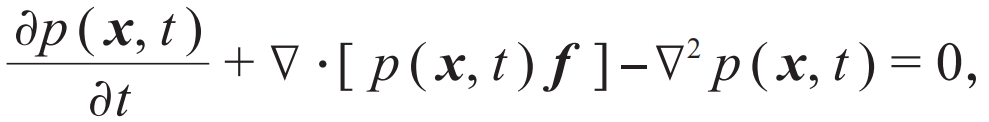 其中f 是(5)式中介绍的得分函数。只要令(8)式中的
其中f 是(5)式中介绍的得分函数。只要令(8)式中的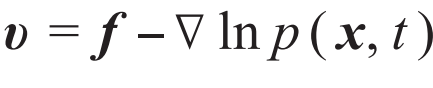 [28,29],就能发现两类模型具有统一的数学形式。这说明其实任何扩散模型背后都隐藏了一个流模型。因此,哪怕是在扩散模型如日中天的时候,也有一小波流模型的信徒坚信,只要找到正确的训练方式,流模型可以做得一样好,甚至更好。终于,2022年的秋天,几篇工作[30—32]几乎同时发现了一种新的训练连续时间流模型的方法:流匹配 (flow matching) 。流匹配方法受到了得分匹配方法的启发,但是它所训练得到的流模型可以比扩散模型更加简洁、灵活、高效,对于追求定量精确的科学问题尤为有用。例如,计算体系在不同构象下的自由能差在很多物理、化学和生物的应用中都非常关键。但是传统计算方法往往依赖于人为设计某种路径,使得在计算模拟过程中构象能够连接起来。而使用流匹配方法估计构象之间的自由能差[33],仅仅需要不同构象下各自的数据样本,具有很强的通用性。
[28,29],就能发现两类模型具有统一的数学形式。这说明其实任何扩散模型背后都隐藏了一个流模型。因此,哪怕是在扩散模型如日中天的时候,也有一小波流模型的信徒坚信,只要找到正确的训练方式,流模型可以做得一样好,甚至更好。终于,2022年的秋天,几篇工作[30—32]几乎同时发现了一种新的训练连续时间流模型的方法:流匹配 (flow matching) 。流匹配方法受到了得分匹配方法的启发,但是它所训练得到的流模型可以比扩散模型更加简洁、灵活、高效,对于追求定量精确的科学问题尤为有用。例如,计算体系在不同构象下的自由能差在很多物理、化学和生物的应用中都非常关键。但是传统计算方法往往依赖于人为设计某种路径,使得在计算模拟过程中构象能够连接起来。而使用流匹配方法估计构象之间的自由能差[33],仅仅需要不同构象下各自的数据样本,具有很强的通用性。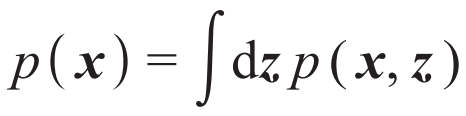 。可是,对于隐变量积分并不好算,这和计算表1中的配分函数和边际似然的难度类似。幸运的是,注意到与(3)式类似的变分自由能原理,我们有:
。可是,对于隐变量积分并不好算,这和计算表1中的配分函数和边际似然的难度类似。幸运的是,注意到与(3)式类似的变分自由能原理,我们有: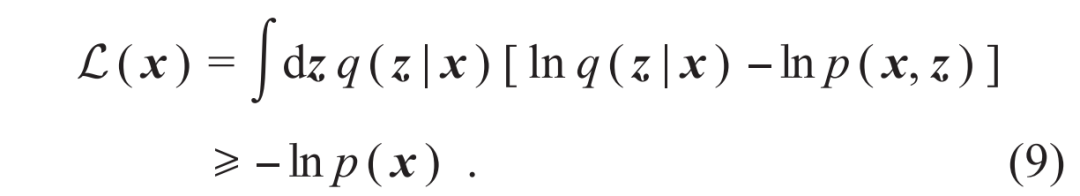
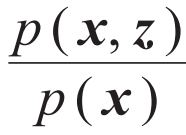 。另一方面,联合概率分布也可以写成
。另一方面,联合概率分布也可以写成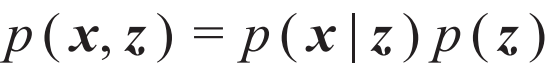 。这里p(z)是隐变量的先验分布,一般被选取为简单的概率分布,而p(x|z)是解码器,相当于一个从低维隐变量空间出发生成高维数据的生成模型。(9)式这样的不等式是变分自编码器名字中“变分”一词的来源。表2总结了变分自编码器和变分自由能(3)式的对应关系。
。这里p(z)是隐变量的先验分布,一般被选取为简单的概率分布,而p(x|z)是解码器,相当于一个从低维隐变量空间出发生成高维数据的生成模型。(9)式这样的不等式是变分自编码器名字中“变分”一词的来源。表2总结了变分自编码器和变分自由能(3)式的对应关系。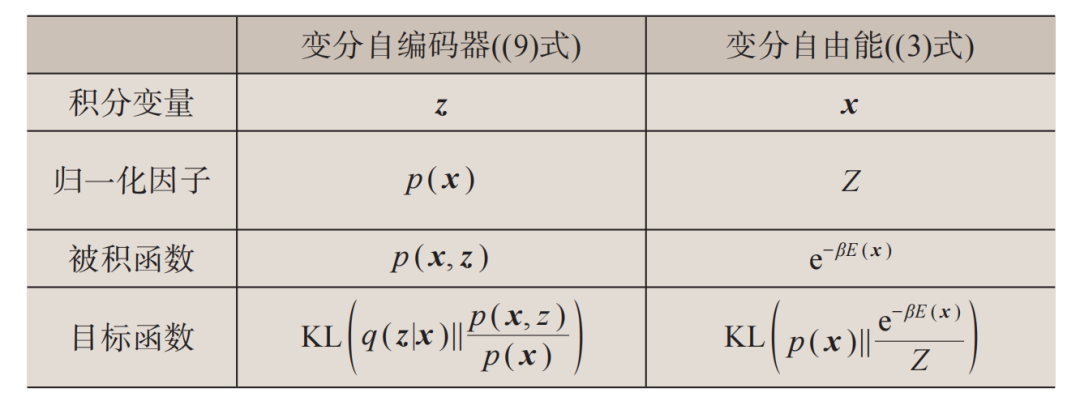
4. 应用于物质科学的生成模型
4. 应用于物质科学的生成模型
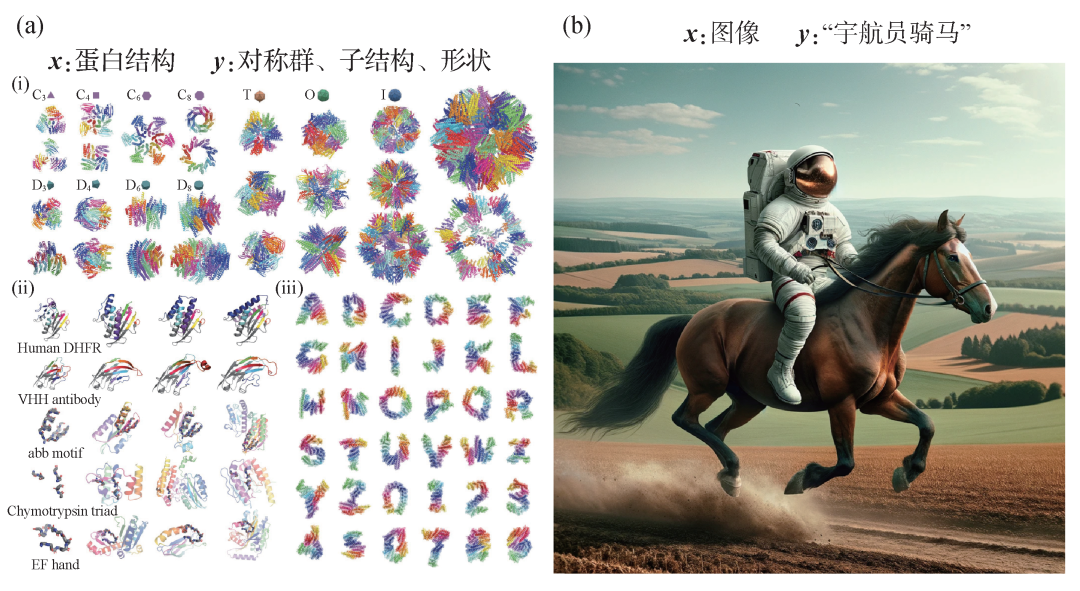
图3 (a)Chroma基于对称性(i)、子结构(ii)和形状(iii)生成的蛋白结构[37];(b)DaLLE-3基于文字提示生成图片[38]
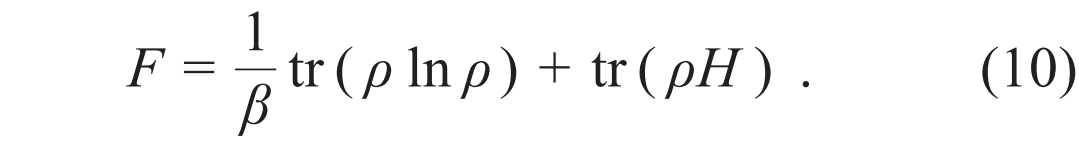
 ,其中k是标记多电子能级的量子数,p(k)是能级占据的经典概率分布。可以使用自回归模型表达这个离散变量的联合概率分布,它的物理含义就是费米液体的朗道能量泛函。另一方面,
,其中k是标记多电子能级的量子数,p(k)是能级占据的经典概率分布。可以使用自回归模型表达这个离散变量的联合概率分布,它的物理含义就是费米液体的朗道能量泛函。另一方面,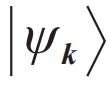 是正交归一的多电子波函数,类比于前文(7)式,可以用“开根号”的流模型参数化这簇多体波函数:
是正交归一的多电子波函数,类比于前文(7)式,可以用“开根号”的流模型参数化这簇多体波函数: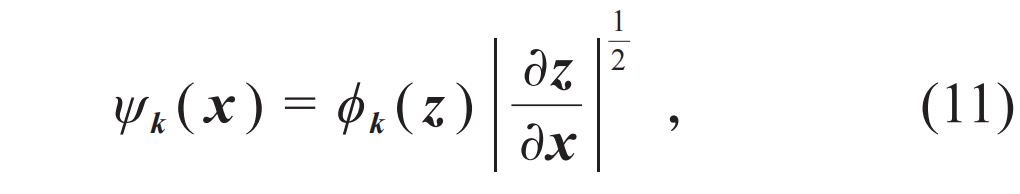
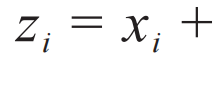
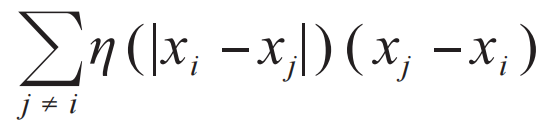 。洄流的物理含义是在相互作用体系中,粒子拖曳周围的粒子形成了准粒子。用准粒子坐标表达的简单波函数,如果写回到粒子坐标就是一个包含了关联效应的多体波函数。从深度学习的角度看,洄流变换对应于一个残差神经网络[54]。因此,其实可以把若干这样的变换串联起来形成图4所示的深层残差神经网络。可见,流模型抓住了费米液体理论中关键的绝热连续性 (adiabatic continuity) 的概念,而凝聚态物理学家讨论的准粒子就生活在流模型的隐变量空间。
。洄流的物理含义是在相互作用体系中,粒子拖曳周围的粒子形成了准粒子。用准粒子坐标表达的简单波函数,如果写回到粒子坐标就是一个包含了关联效应的多体波函数。从深度学习的角度看,洄流变换对应于一个残差神经网络[54]。因此,其实可以把若干这样的变换串联起来形成图4所示的深层残差神经网络。可见,流模型抓住了费米液体理论中关键的绝热连续性 (adiabatic continuity) 的概念,而凝聚态物理学家讨论的准粒子就生活在流模型的隐变量空间。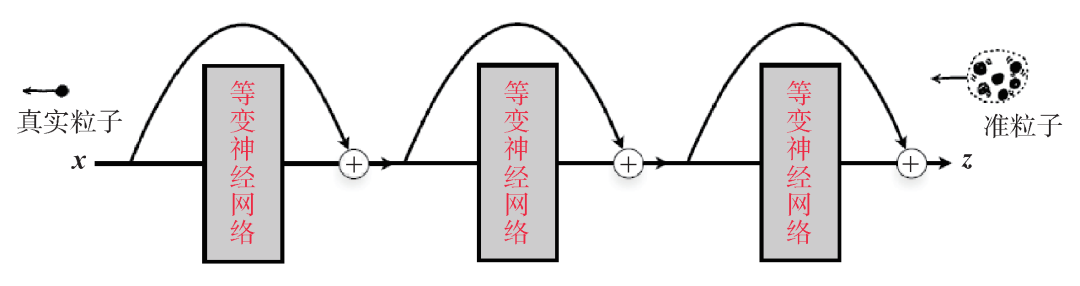
图4 使用深层的残差神经网络实现粒子和准粒子坐标之间的洄流变换。为了保证准粒子的统计性质,神经网络变换需要满足置换等变性质,即粒子置换操作和神经网络变换对易
5. 结语
5. 结语

致谢 本文的写作受益于与张林峰、王涵、尤亦庄、吕健、李烁辉、谢浩、刘金国、吴典、董馨阳、欧仕刚等的合作与讨论。
(参考文献可上下滑动查看)
AI By Complexity读书会招募中
大模型、多模态、多智能体层出不穷,各种各样的神经网络变体在AI大舞台各显身手。复杂系统领域对于涌现、层级、鲁棒性、非线性、演化等问题的探索也在持续推进。而优秀的AI系统、创新性的神经网络,往往在一定程度上具备优秀复杂系统的特征。因此,发展中的复杂系统理论方法如何指导未来AI的设计,正在成为备受关注的问题。
集智俱乐部联合加利福尼亚大学圣迭戈分校助理教授尤亦庄、北京师范大学副教授刘宇、北京师范大学系统科学学院在读博士张章、牟牧云和在读硕士杨明哲、清华大学在读博士田洋共同发起「AI By Complexity」读书会,从复杂网络、统计物理、算法信息论、因果涌现、自由能原理、自组织临界等视角出发,探讨如何理解复杂系统的机制,这些理解是否可以启发我们设计更好的AI模型。读书会于6月10日开始,每周一晚上20:00-22:00举办。欢迎从事相关领域研究、对AI+Complexity感兴趣的朋友们报名读书会交流!
AI+Science 读书会
点击“阅读原文”,报名读书会











