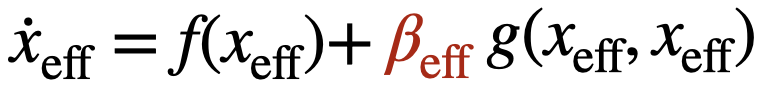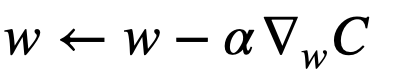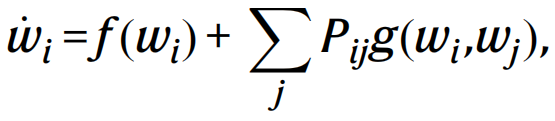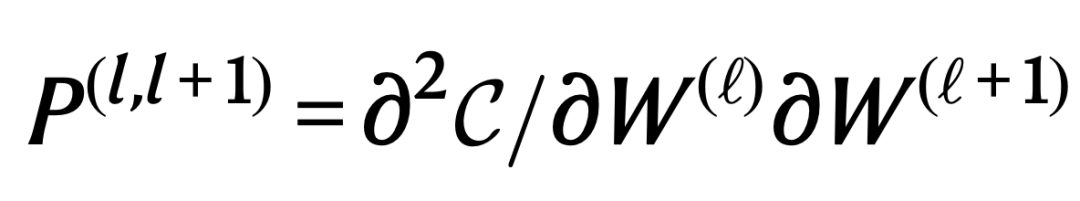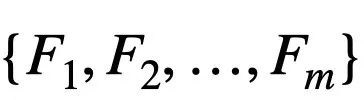机器学习已经渗透到现代社会的方方面面,深刻影响了从AlphaGo到ChatGPT等新兴技术的发展与变革,强劲助推手机、汽车等消费产品的智能化的进程。在机器学习中,人工神经网络模型则扮演着举足轻重的角色。由于神经网络复杂的结构、数量不等的超参数、含有随机扰动的多种数据形式,我们缺乏一个统一的框架形象地揭示其底层的学习机制。为此,我们基于网络科学的平均场理论,开发出一个简洁的数学框架,将基于梯度下降的神经网络模型学习过程转化为网络动力学模型的演化过程,以此推导出一个基于神经网络的拓扑结构指标。根据这个指标可以以很低的训练成本,有效地预测神经网络模型收敛状态下的预测性能。将其应用到迁移学习,实现神经网络模型的筛选,在17个预训练的ImageNet模型、五个基准数据集、一个NAS基准上的实验结果表明,我们可以有效地对神经网络模型排名,筛选出最佳的模型。
在集智俱乐部「AI by complexity」读书会,谷歌软件工程师、美国伦斯勒理工 (RPI) 计算机博士蒋春恒介绍了发表于 Nature Communications 的这项最新研究,欢迎感兴趣的朋友加入读书会观看视频回放。
研究领域:机器学习,神经网络、模型筛选、网络科学、平均场、迁移学习
蒋春恒 | 作者

Network properties determine neural network performance
论文链接:
https://www.nature.com/articles/s41467-024-48069-8
神经网络模型是深度学习领域的主流模型,其训练主要依赖于反向传播机制,根据模型预测误差不断更新迭代模型权值,使得模型精度不断改善。对于某一种任务,比如ImageNet上的分类,存在各种类型的神经网络模型,比如AlexNet,ResNet,VGGNet,Inception,我们如何从中筛选出最适合这一任务的模型显得尤为重要。传统的方法是直接针对ImageNet,从头训练各种类型的神经网络模型。这种方法存在一个明显的问题:对于大型的数据集和复杂的神经网络模型,训练成本是一个很严重的问题。另外一个相关的问题是当任务改变时,我们需要对不同的数据集重新训练模型。为此,人们提出迁移学习的概念,将在任务A中学习到的知识迁移到另外一项任务B,比如使用相同的神经网络模型,然后不同的输出层,保持底层模型状态,只对任务B训练输出层。这一过程称作模型微调。纵使如此,模型精调的成本仍然很高。
本文从复杂网络的视角提出一种新的框架,建立网络模型学习与复杂网络动力学模型演化之间的等价关系,将神经网络映射到网络图,应用平均场理论推导出一个简单的网络拓扑指标,用来预测模型完整训练收敛状态的预测精度。
高建喜教授根据平均场理论提出一种衡量网络韧性的指标。我们这里简单介绍一下复杂网络系统、平均场以及网络韧性之间的关系。
对于很多复杂网络系统,可以使用如下的微分方程方程组表示个体(结点)之间的相互影响

如果网络系统规模很小,我们可以根据提供的初始值进行前向欧拉迭代,快速找到模型的稳态解(当然某些系统可能不存在稳态解,这里不予讨论)。但是当网络系统规模达到百万级别时,这种前向迭代求解的方法效率会大打折扣。为此,高建喜等人提出一种基于平均场理论的维度约简方法,将耦合的多元微分方程组降至多个一元微分方程组。他们引入一个算子
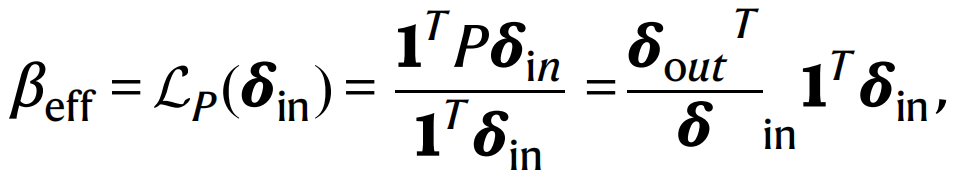
其中,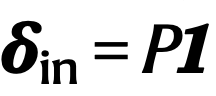 是网络的入度,
是网络的入度,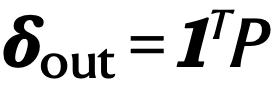 是网络的出度。这个指标可以有效地度量网络的韧性,即网络在当前状态下如果承受一些扰动,比如生态网络中某些物种种群数量变小甚至消失,是否还能够恢复到扰动之前的状态。
对于网络中的某个节点i,状态xi,那我们应用如上的算子,可以确定如下的关系
既然βeff只依赖于网络的拓扑结构,不依赖于网络的状态信息,可以直接快速地算出。如果求解以上的方程可以确定xeff,如此可以并行地快速求解多个一元微分方程组,确定模型的稳态解。
对于神经网络模型,我们训练的目的是确定模型收敛时模型的可训练参数。我们能否建立起关于神经网络模型训练的动力学模型呢?答案是肯定的。
是网络的出度。这个指标可以有效地度量网络的韧性,即网络在当前状态下如果承受一些扰动,比如生态网络中某些物种种群数量变小甚至消失,是否还能够恢复到扰动之前的状态。
对于网络中的某个节点i,状态xi,那我们应用如上的算子,可以确定如下的关系
既然βeff只依赖于网络的拓扑结构,不依赖于网络的状态信息,可以直接快速地算出。如果求解以上的方程可以确定xeff,如此可以并行地快速求解多个一元微分方程组,确定模型的稳态解。
对于神经网络模型,我们训练的目的是确定模型收敛时模型的可训练参数。我们能否建立起关于神经网络模型训练的动力学模型呢?答案是肯定的。
神经网络模型的应用场景很多,常见地比如图像识别、语音识别、自然语言处理。我们这里主要考察的是图像识别的任务。神经网络模型训练的目标是根据模型对输入图像的预测偏差,调整模型参数。模型的参数是建立在一个预测和图像类别上的误差函数,模型训练本质上是一个数学优化问题。具体而言,我们需要不断的更新模型参数,降低模型的预测误差,等价而言就是提升模型的预测精度。模型参数更新或者误差函数优化最常见的一种方法是随机梯度下降法:
其中C是一个含参的误差函数,模型参数的更新本质上是一个动力学系统。模型训练的过程是由这个反向传播的动力系统所驱动。
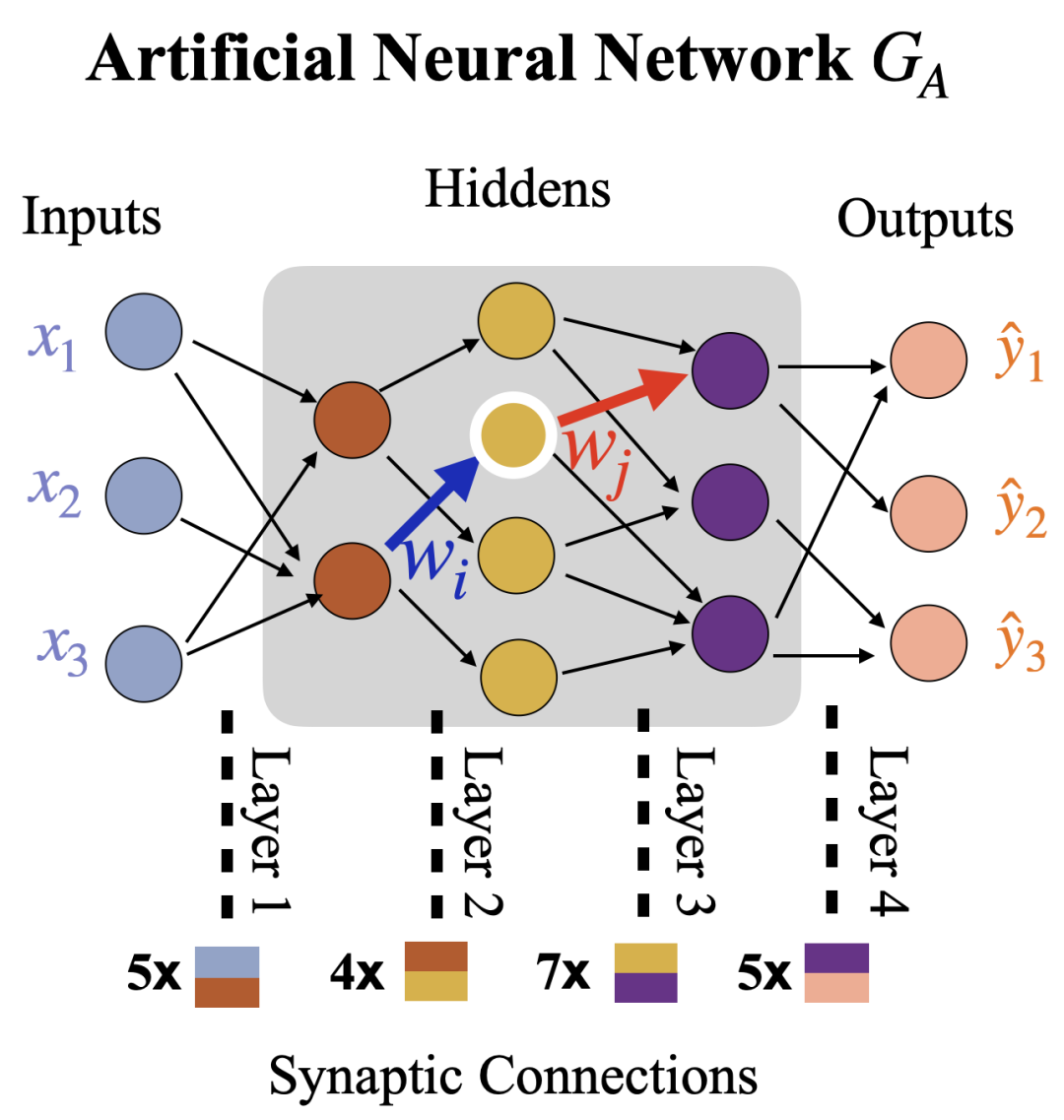
我们使用如下简单的MLP模型来解释神经网络模型训练过程与复杂网络之间的关系。
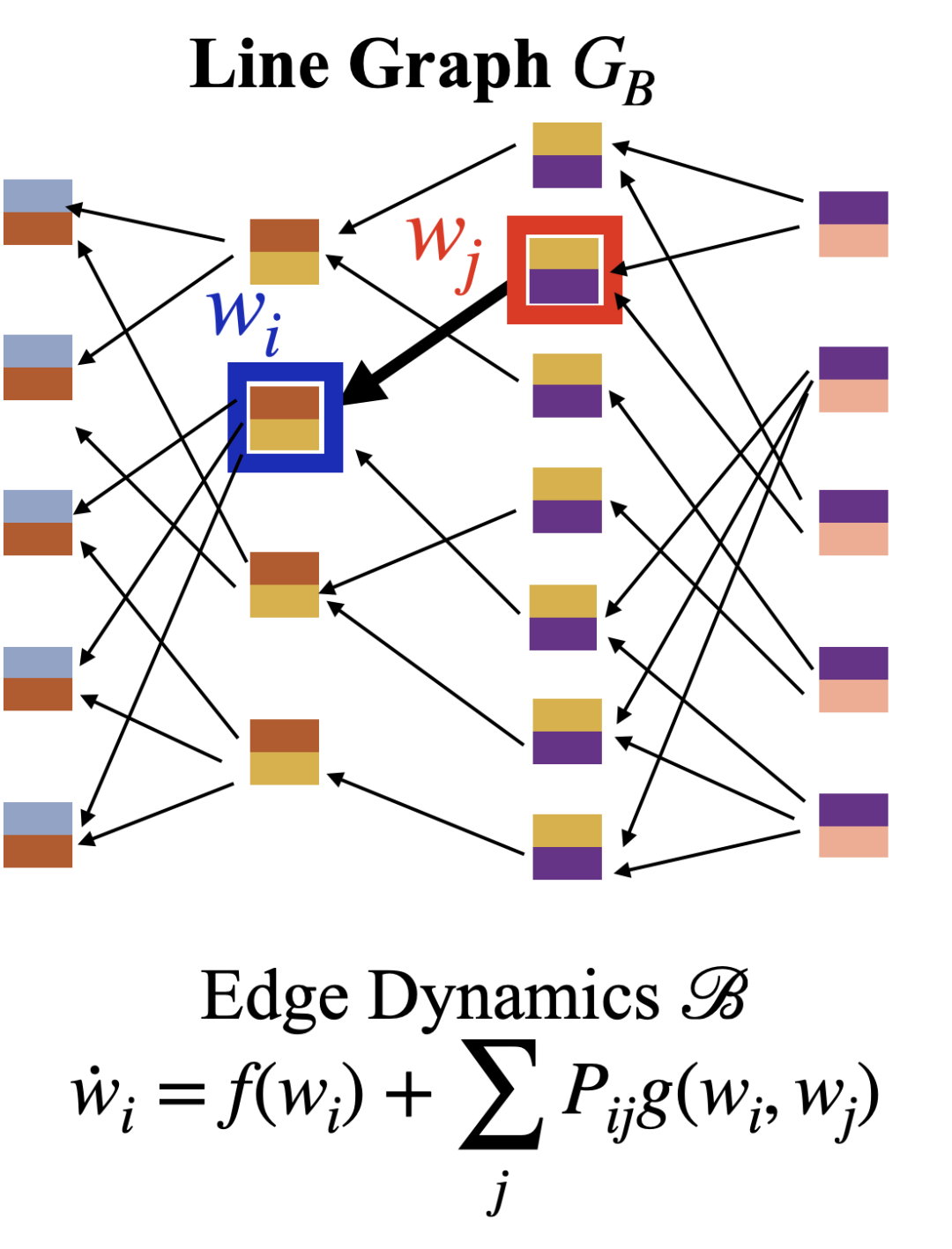
我们需要注意的一点是这里的动力学系统的状态描述的是神经网络模型的权值,而权值对应到神经元之前的突触连接。简单而言,这种状态是对应到神经网络上边的权值。复杂网络动力学模型的状态则对应复杂网络的结点。为了能够利用复杂网络建立对神经网络的认识,我们做出如下的转化:直接建立一个关于神经网络边的有向网络。
我们顺着反向传播的方向建立如上图所示的一个有向图,图中每个节点对应着神经网络的一个边(严格而说是对应神经网络的一个可训练的参数)。如果在神经网络GA中,从参数wj到wi存在一个路径(经由一个中介神经元),我们就在GB上建立一个从wj到wi的边。我们如果要建立一个严格的动力学系统,还需要确定这些参数之间的相互影响以及影响的强度,即邻接矩阵P。这个是我们应用复杂网络关于网络韧性相关结论的前提。
我们对基于SGD的模型更新过程建立起关于神经网络参数的一个近似的动力学模型
我们使用关于误差函数的二阶偏导,确定神经网络相邻层参数对的相互影响强度,并以此确定相应微分方程的P:
我们应用高建喜教授提出的网络韧性指标到这个微分方程,可以确定一个对应于神经网络模型训练的韧性指标。对于神经元刺激函数是ReLu的神经网络,我们发现当模型收敛时,模型对应的βeff=0。我们将这一发现应用到模型筛选问题。
模型筛选是给定一个具体的任务,比如图像分类,还有一组备选的神经网络模型
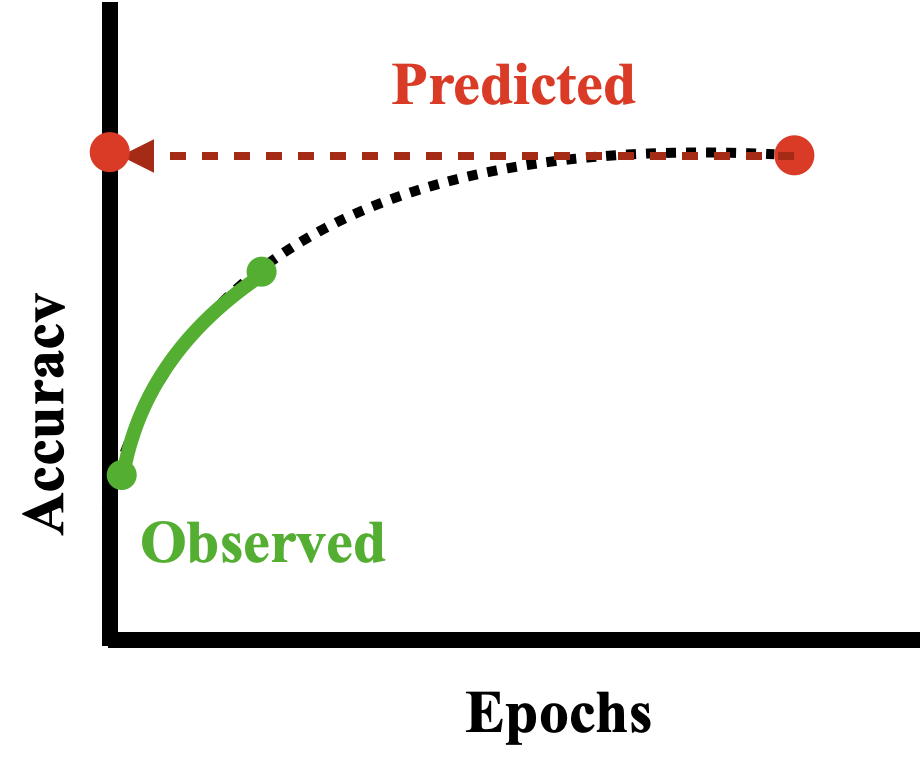
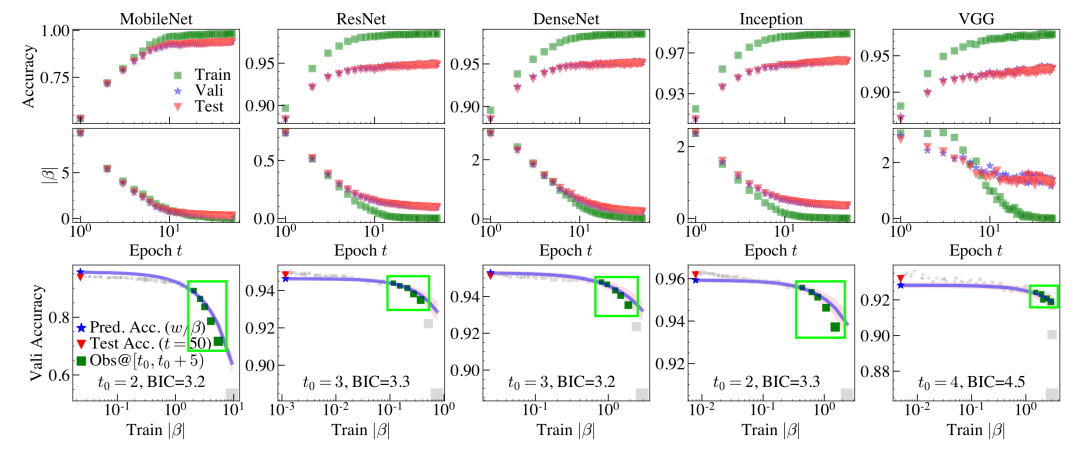
如果对于每个模型,我们都从头开始训练,那么训练成本无疑是巨大的,尤其是当目标数据集很庞大,模型本身又很复杂的情况下。为此,有人提出对这些模型只做部分训练,比如训练50个Epoch,然后用部分训练中所收集的相关信息,比如模型参数、训练数据的batch尺寸、模型训练的超参数等,拟合出这些信息和模型预测精度的关系,表示成学习曲线:
目标就在根据学习曲线确定模型最终(比如100个epoch)的预测精度。
这些方法存在一些明显的问题,比如我们收集大量的部分训练的数据,即观测部分的学习曲线;缺乏理论基础,我们无法确定模型需要训练多久才算收敛,学习曲线的走势如何等等问题。
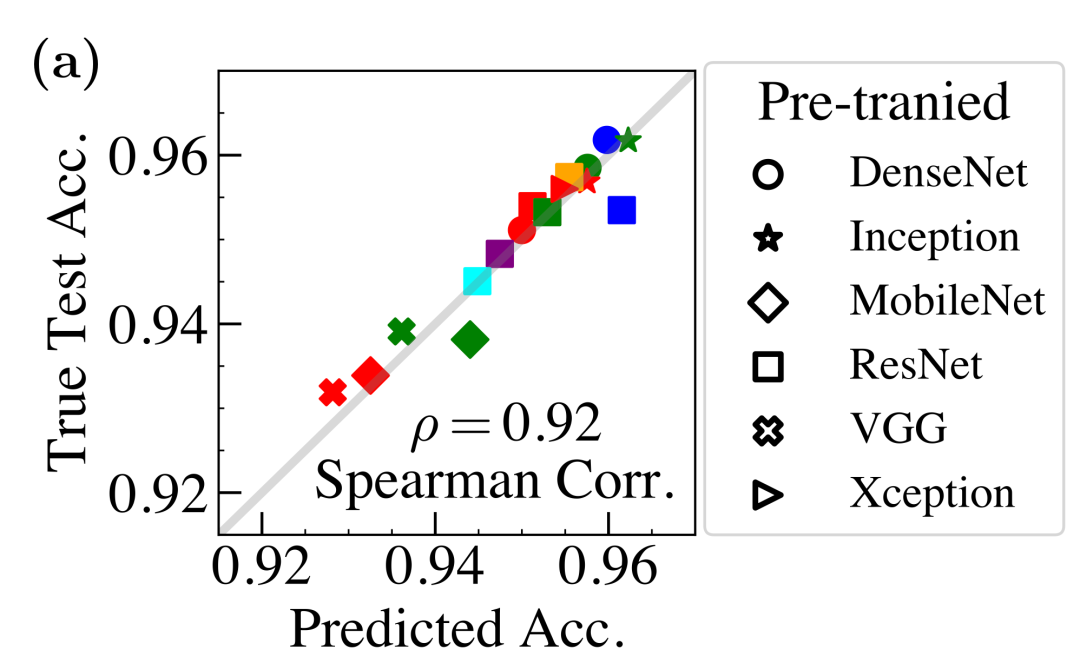
我们提出的方法可以利用我们模型收敛时的状态,即βeff=0确定模型最终的预测精度。将其应用到迁移学习问题,测试筛选Keras中比较流行的一些预训练模型,可以发现我们的方法准确地筛选出高质量的模型:
目前我们分析的模型还仅仅局限于ReLU神经网络,能否将其应用到一般性的神经网络模型呢,比如扩展到RNN、Transformer?我们是否可以更有效的确定模型训练过程中模型参数之间的相互影响,从而建立更为精确的交互模型呢?比如确定更为准确的f和g,并利用并行化的方式快速求解模型的稳态解?或许从模型训练的类时间序列中直接建立模型训练所对应的动力学方程,乃至复杂网络图表示。对于利用网络拓扑指标优化模型设计与搜索,我们可否提出一种有效的神经网络的复杂网络图表示,以此进行增量式的自动化搜索,比如网络重连 (rewiring) ?
Gao, J., Barzel, B. & Barabási, A.-L. Universal resilience patterns in complex networks. Nature 530, 307–312 (2016).
Lillicrap, T. P., Santoro, A., Marris, L., Akerman, C. J. & Hinton, G. Backpropagation and the brain. Nat. Rev. Neurosci. 1–12 (2020).
Chandrashekaran, A. & Lane, I. R. Speeding up hyper-parameter optimization by extrapolation of learning curves using previous builds. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases, 477–492 (Springer, 2017).
Nguyen, C., Hassner, T., Seeger, M. & Archambeau, C. LEEP: A new measure to evaluate transferability of learned representations. In International Conference on Machine Learning, 7294–7305 (PMLR, 2020).
Mellor, J., Turner, J., Storkey, A. & Crowley, E. J. Neural architecture search without training. In International Conference on Machine Learning, 7588–7598 (PMLR, 2021).
Dong, X., Liu, L., Musial, K. & Gabrys, B. NATS-Bench: Benchmarking nas algorithms for architecture topology and size. IEEE Transac. Pattern Anal. Machine Intelligence 7, 3634–3646 (2021).
蒋春恒,谷歌软件工程师,美国伦斯勒理工 (RPI) 计算机博士。主要研究兴趣:人工智能与网络科学、神经网络学习过程的拓扑演化与网络动力学、优化理论。
斑图地址:https://pattern.swarma.org/study_group_issue/719
大模型、多模态、多智能体层出不穷,各种各样的神经网络变体在AI大舞台各显身手。复杂系统领域对于涌现、层级、鲁棒性、非线性、演化等问题的探索也在持续推进。而优秀的AI系统、创新性的神经网络,往往在一定程度上具备优秀复杂系统的特征。因此,发展中的复杂系统理论方法如何指导未来AI的设计,正在成为备受关注的问题。
集智俱乐部联合加利福尼亚大学圣迭戈分校助理教授尤亦庄、北京师范大学副教授刘宇、北京师范大学系统科学学院在读博士张章、牟牧云和在读硕士杨明哲、清华大学在读博士田洋共同发起「AI By Complexity」读书会,探究如何度量复杂系统的“好坏”?如何理解复杂系统的机制?这些理解是否可以启发我们设计更好的AI模型?在本质上帮助我们设计更好的AI系统。读书会于6月10日开始,每周一晚上20:00-22:00举办。欢迎从事相关领域研究、对AI+Complexity感兴趣的朋友们报名读书会交流!
![]()
点击“阅读原文”,报名读书会



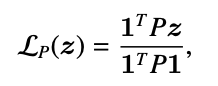
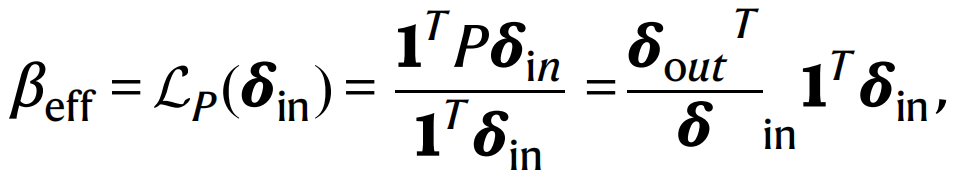
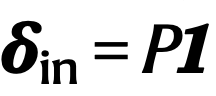 是网络的入度,
是网络的入度,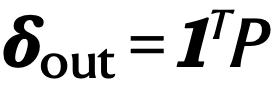 是网络的出度。这个指标可以有效地度量网络的韧性,即网络在当前状态下如果承受一些扰动,比如生态网络中某些物种种群数量变小甚至消失,是否还能够恢复到扰动之前的状态。
是网络的出度。这个指标可以有效地度量网络的韧性,即网络在当前状态下如果承受一些扰动,比如生态网络中某些物种种群数量变小甚至消失,是否还能够恢复到扰动之前的状态。