导语


“复杂世界，简单规则。”

集智俱乐部联合复旦大学智能复杂体系实验室青年研究员朱群喜、浙江大学百人计划研究员李樵风、清华大学电子工程系数据科学与智能实验室博士后研究员丁璟韬、美国东北大学物理系Albert-László Barabási指导的博士后高婷婷、北京大学博雅博士后曹文祺、复旦大学数学科学学院应用数学方向博士研究生赵伯林、北京师范大学系统科学学院博士研究生牟牧云，共同发起「复杂系统自动建模」读书会第二季。

读书会将于9月7日每周六晚上20:00-22:00进行，探讨四个核心模块：数据驱动的复杂系统建模、复杂网络结构推断、具有可解释性的复杂系统推断（动力学+网络结构）、应用-超材料设计和城市系统，通过重点讨论75篇经典、前沿的重要文献，从黑盒（数据驱动）到白盒（可解释性），逐步捕捉系统的“本质”规律，帮助大家更好的认识、理解、预测、控制、设计复杂系统，为相关领域的研究和应用提供洞见。欢迎感兴趣的朋友报名参与！




读书会背景




复杂系统由大量相互交互的元素构成并产生复杂的集体行为，在自然界和人类社会中广泛存在，例如大脑神经元网络、鸟群、交通网络、疾病传播等。研究复杂系统的建模和调控对于理解和引导复杂系统的行为具有重要意义。


  • 面对一个真实的复杂系统，我们如何提炼底层的机制、构建简单模型？

  • 这些把握住系统本质的简单规则从何而来？

  • 对于更复杂的系统，例如基因调控系统、社会经济系统，我们面对庞杂的数据和复杂的系统状态，要如何做出假设？

  • 随着深度学习技术的发展，有没有可能设计出一个自动化的系统，根据不同的任务需求，能够通过观察数据，或者是洞察规律，对各式复杂系统建模？

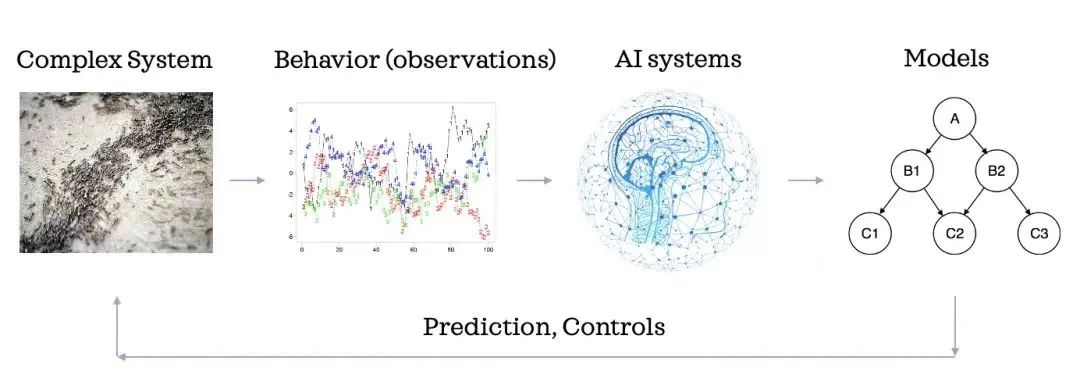
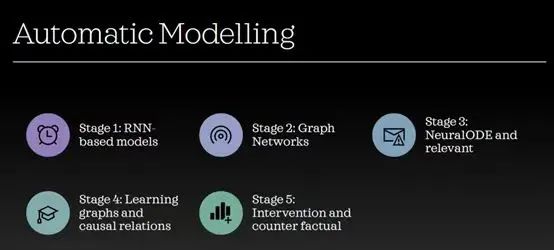
这些核心的问题，都迫切需要我们有更好的方法和手段，去理解复杂系统的内部机制、预测系统的未来行为，从而能够更有效地干预和控制复杂系统。

早在2020年，集智俱乐部联合北京师范大学教授张江发起了复杂系统自动建模读书会第一季，重点梳理了AI自动建模的流程以及AI自动建模的五个发展阶段，是该领域最早的综述性分享之一。随着近年来深度学习技术的发展，这个领域有了更多的学者关注，新的研究方法也如雨后春笋般涌现。为此，我们组织第二季读书会，旨在帮助集智社区成员更深入地了解该领域的最新进展，探讨未来的研究方向。





读书会框架




当前复杂系统建模研究主要聚焦于三个核心领域：

  • 首先，时间维度上的动力学建模，旨在捕捉系统随时间演化的特性；

  • 其次，空间维度上的元素交互关系建模，致力于揭示系统内部组成单元之间的相互作用机制；

  • 最后，基于对复杂系统的既有认知和理解，探索系统的定向设计方法。

这三个方面的研究相辅相成，共同推动了复杂系统建模的全面发展。

所以本季读书会，我们围绕着三个核心问题，设计了四个核心模块，包含了17种不同类型的方法，涉及到75篇经典、前沿的重要文献。


我们希望通过研读这些文献，从黑盒（数据驱动）到白盒（可解释性），逐步捕捉系统的“本质”规律，帮助大家更好的认识、理解、预测、控制、设计复杂系统，为相关领域的研究和应用提供洞见。




发起人介绍




朱群喜，复旦大学智能复杂体系实验室青年研究员。致力于复杂系统和机器学习前沿的理论与方法研究，在复杂系统建模、重构、预测和智能调控以及复杂系统驱动的机器学习领域做出了一系列工作，相关成果以第一或通讯作者在综合性、控制、数学、物理、人工智能等顶级/一流学术刊物发表文章20余篇，研究成果得到同行大家的关注和引用 (Edward Ott、Jürgen Kurths、曹进德、桂卫华等院士, Google Research、UC Berkeley、牛津大学、剑桥大学和麻省理工等知名教授专家团队)， 以及国际知名学术/科技网站的报道(Phys.org, techxplore.com)。
个人主页：qunxizhu.cn

李樵风，浙江大学百人计划研究员，博士生导师，获国家高层次人才计划（海外）资助。主要研究方向包括：基于人工智能的科学计算、智能系统感知、复杂结构动力学反问题等。到目前为止，在PRL、Science Robotics、EML、MSSP、Applied Energy等领域重要期刊上发表论文20篇。
课题组主页：https://www.ligroupzju.com

丁璟韬，清华大学电子工程系数据科学与智能实验室博士后研究员，于清华大学电子工程系获得学士、博士学位，主要研究方向为AI驱动的时空复杂系统生成式建模及应用，在NeurIPS、ICLR、KDD、WWW、AAAI、IJCAI等国际会议与期刊发表学术论文50余篇，担任PLOS Complex Systems的学术编辑（Academic Editor）以及KDD、NeurIPS、ICML、ICLR、AAAI等国际会议的程序委员会委员（PC member），曾获2018年国际万维网大会（WWW 2018）最佳海报论文奖、国际会议IEEE IWCWC 2019、ACM HotPOST 2015最佳论文奖。
主页 https://scholar.google.com/citations?user=_TAJECAAAAAJ

高婷婷，美国东北大学物理系博士后，由Albert-László Barabási教授指导；博士毕业于同济大学，导师为严钢教授。主要研究方向为数据驱动的复杂网络推断理论及应用，开发了用于从含噪和不完整数据中推断复杂网络ODE的Two-Phase推断框架，以及基于消息传递机制的、从随机动力学系统观测数据推断复杂系统SDE的LaGNA框架；目前的研究兴趣主要为AI for Complex System和物理网络（Physical Network）的理论及应用。


曹文祺，北京大学博雅博士后。博士毕业于上海交通大学控制科学与工程专业，曾访问意大利帕多瓦大学、日本玉川学院等。研究兴趣为低秩随机过程理论的建模与估计，发表论文十余篇，包括IEEE Transactions on Automatic Control，Automatica，SIAM Journal on Optimization and Control等长文。荣获国家资助博士后研究人员计划、北京大学博雅博士后项目资助。https://www.researchgate.net/profile/Wenqi-Cao-2 。

赵伯林，复旦大学数学科学学院应用数学方向博士研究生，主要研究方向为复杂系统与机器学习的交叉领域，包括复杂动力系统的建模、预测、辨识、变点检测以及因果推断。
https://www.researchgate.net/profile/Bolin-Zhao-5

牟牧云，北京师范大学系统科学学院博士生，张江老师因果涌现研究小组成员。研究方向：复杂系统建模与调控、强化学习世界模型。




报名参与读书会




运行模式

从2024年9月7日开始，周六20:00-22:00，持续时间预计 8-10 周左右，按读书会框架设计，每周进行线上会议，与主讲人等社区成员当面交流，会后可以获得视频回放持续学习。


报名方式

第一步：扫码填写报名信息。

扫码报名（可开发票）

第二步：填写信息后，付费报名。

如需用支付宝支付，请在PC端进入读书会页面报名支付：https://pattern.swarma.org/study_group/51

第三步：添加运营负责人微信，获取所有推荐论文资源包，拉入对应主题的读书会社区（微信群）。

PS：为确保专业性和讨论的聚焦，本读书会谢绝脱离读书会主题和复杂科学问题本身的空泛的哲学和思辨式讨论；如果出现讨论内容不符合要求、经提醒无效者，会被移除群聊并对未参与部分退费。

加入社区后可以获得的资源：

完整权限，包括线上问答、录播回看、资料共享、社群交流、信息同步、共创任务获取积分等。


参与共创任务获取积分，共建学术社区：

读书会采用共学共研机制，成员通过内容共创获积分（字幕修改、读书会笔记、论文速递、公众号文章、集智百科、论文解读等共创任务），积分符合条件即可退费。发起人和主讲人同样遵循此机制，无额外金钱激励。

PS：具体参与方式可以加入读书会后查看对应的共创任务列表，领取任务，与运营负责人沟通详情，上述规则的最终解释权归集智俱乐部所有。





领域必读文献清单




阅读材料较丰富，为了更好的阅读体验，建议您前往集智斑图沉浸式阅读，并可收藏感兴趣的论文，下载推荐阅读的论文以及代码，查看更多相关学习资源。
读书会阅读清单


模块一：数据驱动的复杂系统建模

随着科技的飞速进步，我们已经积累了很多关于复杂系统运作的数据，尤其是系统生成的时间序列数据。传统复杂系统研究基于领域知识建立微观交互模型，并据此优化控制系统。但对真实复杂系统构建全面模型极为困难。
近年来，数据驱动方法成为热点，利用人工智能算法自动构建高精度模型。这种方法不仅能更精确地分析、模拟和预测复杂系统，还为系统控制和优化提供了新的可能性。

储备池计算

推荐语：第一篇文章利用储备池计算预测时空混沌系统；第二篇文章梳理了储备池计算的研究进展；第三篇文章提出了一种基于格兰杰因果和储备池计算的轻量化机器学习框架，可以揭示系统高阶相互作用，并利用这些高阶结构信息进行精准动力学预测。
  • Pathak, J., Hunt, B., Girvan, M., Lu, Z., & Ott, E. (2018). Model-free prediction of large spatiotemporally chaotic systems from data: A reservoir computing approach. Physical review letters, 120(2), 024102.
  • Yan, M., Huang, C., Bienstman, P., Tino, P., Lin, W., & Sun, J. (2024). Emerging opportunities and challenges for the future of reservoir computing. Nature Communications, 15(1), 2056.
  • Li, X., Zhu, Q., Zhao, C., Duan, X., Zhao, B., Zhang, X., … & Lin, W. (2024). Higher-order Granger reservoir computing: simultaneously achieving scalable complex structures inference and accurate dynamics prediction. Nature Communications, 15(1), 2506. | 本篇文献介绍可见：Nat. Commun. 前沿：数据驱动的复杂系统高阶结构推断与动力学预测


物理知识引导的神经网络架构

推荐语：第一篇文章将物理规律引入到神经网络架构之中；第二篇文章综述了动力系统中的现代Koopman理论；第三篇文章构建了数理先验信息嵌入式的机器学习框架，哈密顿神经Koopman算子。

  • Greydanus, S., Dzamba, M., & Yosinski, J. (2019). Hamiltonian neural networks. Advances in neural information processing systems, 32.

  • Brunton, S. L., Budišić, M., Kaiser, E., & Kutz, J. N. (2021). Modern Koopman theory for dynamical systems. arXiv preprint arXiv:2102.12086.

  • Zhang, J., Zhu, Q., & Lin, W. (2024). Learning Hamiltonian neural Koopman operator and simultaneously sustaining and discovering conservation laws. Physical Review Research, 6(1), L012031. | 本篇文献介绍可见：复旦大学智能复杂体系实验室团队提出了数理先验信息嵌入式机器学习框架

  • Cranmer, M., Greydanus, S., Hoyer, S., Battaglia, P., Spergel, D., & Ho, S.  (2020). Lagrangian Neural Networks. In ICLR 2020 Workshop on Integration of Deep Neural Models and Differential Equations.

  • Rao, C., Ren, P., Wang, Q., Buyukozturk, O., Sun, H., & Liu, Y. (2023). Encoding physics to learn reaction–diffusion processes. Nature Machine Intelligence, 5(7), 765-779.

推荐语：利用网络重整化群启发的神经网络识别大规模复杂网络的关键“骨架”，捕捉长期演化模式，进行高效且精准的动力学模拟。

  • Predicting Long-term Dynamics of Complex Networks via Identifying Skeleton in Hyperbolic Space. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining.


神经微分方程

推荐语：第一篇文章是NeurIPS 2018 的 best paper，构建了连续时间的神经网络框架；第二篇文章指出了经典Neural ODEs的表示能力问题，并提出了增维的Neural ODEs；第三篇文章将时滞引入Neural ODEs中，提出了神经时滞微分方程(Neural DDEs)，解决了经典Neural ODEs的表示能力问题。
  • Chen, R. T., Rubanova, Y., Bettencourt, J., & Duvenaud, D. K. (2018). Neural ordinary differential equations. Advances in neural information processing systems, 31.
  • Dupont, E., Doucet, A., & Teh, Y. W. (2019). Augmented neural odes. Advances in neural information processing systems, 32.
  • Zhu, Q., Guo, Y., & Lin, W. (2021). Neural delay differential equations. The Ninth International Conference on Learning Representations (ICLR 2021).

小样本下的数据驱动建模：可解释性->泛化性->鲁棒性
推荐语：面向物理的数据驱动建模难以采用流行的大数据+大模型范式。这是因为一没有互联网级的数据积累；二复杂物理系统构造单个数据的成本远超语料、图像的采集。因此必须开发不依赖于大数据集的人工智能方法。下面论文以神经常微分方程为共同技术基础，从可解释性、泛化性、鲁棒性三个递进层次开发小数据集下的人工智能建模方法。
  • Lai, Z., Mylonas, C., Nagarajaiah, S., & Chatzi, E. (2021). Structural identification with physics-informed neural ordinary differential equations. Journal of Sound and Vibration, 508, 116196.
  • Li, Q., Wang, T., Roychowdhury, V., & Jawed, M. K. (2023). Rapidly encoding generalizable dynamics in a Euclidean symmetric neural network. Extreme Mechanics Letters, 58, 101925.
  • Li, Q., Wang, T., Roychowdhury, V., & Jawed, M. K. (2023). Metalearning generalizable dynamics from trajectories. Physical Review Letters, 131(6), 067301. | 本篇文献介绍可见：PRL速递：AI 学习玩弹簧玩具——从轨迹到通用动力学的元学习
  • Ji, W., & Deng, S. (2021). Autonomous discovery of unknown reaction pathways from data by chemical reaction neural network. The Journal of Physical Chemistry A, 125(4), 1082-1092.
  • Li, Q., Chen, H., Koenig, B. C., & Deng, S. (2023). Bayesian chemical reaction neural network for autonomous kinetic uncertainty quantification. Physical Chemistry Chemical Physics, 25(5), 3707-3717.


复杂系统智能控制

推荐语：复杂系统控制综述文章，从统计物理与控制论两种视角讨论了复杂网络控制领域的研究范式和建模方法。
推荐语：数据驱动控制复杂系统领域经典工作
推荐语：基于神经常微分方程学习复杂系统控制信号
  • Böttcher, L., Antulov-Fantulin, N., & Asikis, T. (2022). AI Pontryagin or how artificial neural networks learn to control dynamical systems. Nature communications, 13(1), 333.
推荐语：第一篇文章利用神经网络和李雅普诺夫理论，提出了神经李雅普诺夫控制方法；第二篇将神经李雅普诺夫控制推广到随机版本。
  • Chang, Y. C., Roohi, N., & Gao, S. (2019). Neural lyapunov control. Advances in neural information processing systems, 32.
  • Zhang, J., Zhu, Q., & Lin, W. (2022). Neural stochastic control. Advances in neural information processing systems, 35, 9098-9110.


连续时间生成模型

推荐语：第一篇文章是ICLR 2021杰出论文，提出了基于随机微分方程（SDEs）的生成模型，统一了经典的分数模型和扩散模型；第二篇文章提出了快速训练连续正则流的快速且稳定的流匹配方法；第三篇文章指出了流匹配方法的奇异性问题，并提出了切变流匹配方法。
  • Song, Y., Sohl-Dickstein, J., Kingma, D. P., Kumar, A., Ermon, S., & Poole, B. (2020). Score-based generative modeling through stochastic differential equations. The Ninth International Conference on Learning Representations (ICLR 2021).
  • Lipman, Y., Chen, R. T., Ben-Hamu, H., Nickel, M., & Le, M. (2023). Flow matching for generative modeling. The Eleventh International Conference on Learning Representations (ICLR 2023).
  • Zhu, Q., & Lin, W. (2024). Switched flow matching: Eliminating singularities via switching ODEs, 41st International Conference on Machine Learning (ICML 2024). | 本篇文献介绍可见：ICML2024 |复旦大学智能复杂体系基础理论与关键技术实验室研究团队3篇论文被国际机器学习顶级学术会议录用
对此主题感兴趣的伙伴可以关注 AI by Complexity 读书会：从复杂系统到生成式人工智能


复杂网络降维表达

推荐语：随着复杂系统规模和数据量的增大，对系统简化处理并降维分析成为了复杂系统研究的重要需求。目前，已经有关于以网络为代表的复杂系统的降维分析：

验证了低秩结构在复杂系统中的普遍存在性：

数据驱动下对低秩结构的估计和学习：

  • Cao, W., Picci, G., & Lindquist, A. (2023). Identification of low rank vector processes. Automatica, 151, 110938.

通过优化手段提取复杂网络关键节点：

  • MacLaren, N. G., Barzel, B., & Masuda, N. (2024). Observing network dynamics through sentinel nodes. arXiv preprint arXiv:2408.00045. 

模块二：复杂网络结构推断

复杂系统的建模除了对动力学进行建模，另一方面是空间上组成元素间交互关系的建模。
同时由于复杂系统中元素间存在多种复杂作用，产生非线性、涌现等特性，使系统难以简单描述或理解，同时参数数量的增加有可能快于系统大小的增加，我们既无法把整个系统基于还原论而简单理解为个体的加总，也无法从整体的行为有效推断出系统的确定性质。我们希望有一些方法，能够通过学习空间上组成元素间交互关系，从而可以更深入地理解系统的运行机制。


基于Granger因果的推断方法

格兰杰因果检验是用于时间序列因果推断的经典方法，但传统方法多基于线性模型，与复杂系统的非线性本质不符。近年来，研究者将格兰杰因果与神经网络结合，以更准确地推断非线性复杂系统节点间的因果关系，克服了传统方法的局限性。
推荐语：下述文章利用神经网络将复杂系统建模成一个非线性的向量自回归模型，并通过对神经网络的输入层施加稀疏性约束，找出对预测各个节点最有帮助的节点子集，从而得到节点间的格兰杰因果结构：
  • Tank, A., Covert, I., Foti, N., Shojaie, A., & Fox, E. B. (2021). Neural granger causality. IEEE Transactions on Pattern Analysis and Machine Intelligence, 44(8), 4267-4279.
推荐语：下述文章进一步利用神经微分方程来建模节点的动力学，使得我们可以处理连续性动力系统，并在无穷小的时间间隔下探索节点间的格兰杰因果结构：
  • Bellot, A., Branson, K., & van der Schaar, M. (2021). Neural graphical modelling in continuous-time: consistency guarantees and algorithms. The Ninth International Conference on Learning Representations (ICLR 2021).


基于稀疏辨识的结构推断方法

推荐语：基于动力学方程的稀疏辨识方法，可以将复杂系统的动力学表达式投影到一组事先确定的基函数族上，基于恢复出的动力学方程，推断变量间的因果关系：
  • Casadiego, J., Nitzan, M., Hallerberg, S., & Timme, M. (2017). Model-free inference of direct network interactions from nonlinear collective dynamics. Nature communications, 8(1), 2192.
推荐语：基于稀疏辨识的数据驱动式高阶网络重构
  • Delabays, R., De Pasquale, G., Dörfler, F., & Zhang, Y. (2024). Hypergraph reconstruction from dynamics. arXiv preprint arXiv:2402.00078.


基于常微分方程优化的方法

推荐语：针对高维系统以及动力学存在噪音的情况，恢复动力学以及网络结构
  • Yan, Z., Gui, L., Xu, K., & Lan, Y. (2023). Reconstructing dynamics of complex systems from noisy time series with hidden variables. New Journal of Physics, 25(8), 083011.


基于图神经网络的方法

推荐语：基于变分自编码器与图神经网络，可以同时推断网络结构并进行复杂系统动力学的预测。
对每条边的分布单独建模：
  • Kipf, T., Fetaya, E., Wang, K. C., Welling, M., & Zemel, R. (2018, July). Neural relational inference for interacting systems. In International conference on machine learning (pp. 2688-2697). PMLR.
对一个节点对应的边的集合的分布联合建模：
  • Han, Z., Fink, O., & Kammer, D. S. (2024). Collective relational inference for learning heterogeneous interactions. Nature Communications, 15(1), 3191.


基于Intervention的因果推断方法

推荐语：基于Judea Pearl的因果之梯理论，基于相关性的因果推断往往是不可靠的，我们需要对变量施加干预才能更加准确地衡量变量间的因果效应。
基于干预的图注意力神经网络：
  • Sui, Y., Wang, X., Wu, J., Lin, M., He, X., & Chua, T. S. (2022, August). Causal attention for interpretable and generalizable graph classification. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (pp. 1696-1705).
基于干预的储备池计算神经网络：
  • Zhao, J., Gan, Z., Huang, R., Guan, C., Shi, J., & Leng, S. (2024). Detecting dynamical causality via intervened reservoir computing. Communications Physics, 7(1), 232.
基于约束优化学习有向无环图：
  • Brouillard, P., Lachapelle, S., Lacoste, A., Lacoste-Julien, S., & Drouin, A. (2020). Differentiable causal discovery from interventional data. Advances in Neural Information Processing Systems, 33, 21865-21877.
基于贝叶斯方法：
  • Tigas, P., Annadani, Y., Jesson, A., Schölkopf, B., Gal, Y., & Bauer, S. (2022). Interventions, where and how? experimental design for causal models at scale. Advances in neural information processing systems, 35, 24130-24143.


模块三：具有可解释性的复杂系统推断（动力学+网络结构）

G. Bianconi等编辑在2021年的《物理学杂志：复杂》（《Journal of Physics: Complexity》）纪念专刊：《聚光灯下的复杂系统: 2021年诺贝尔物理学奖后的下一步》（《Complex systems in the spotlight: next steps after the 2021 Nobel Prize in Physics》）中，对复杂性的预测进行了探讨。本篇文献介绍可见：吕琳媛：2021年诺奖后，复杂科学未来二十年的重大挑战是什么？
大家一致认为，复杂系统是最难预测的系统之一，原因如下：
  1. 系统具有超高维度、高度非线性和不确定性
  2. 对初始值敏感，表现出混沌特性
  3. 某些系统会根据预测结果进行调整和反馈，影响长期预测
  4. 普遍存在随机效应
为提升复杂系统的预测能力和可解释性，至关重要的是深入探究其底层动力学机制。因此，开发具有可解释性的复杂系统建模方法成为重中之重，这种方法需能同时对系统的动力学和网络结构进行精确建模。通过这种综合性的建模方法，我们可以更全面地理解和分析复杂系统的内在机制，从而提高预测精度并增强模型的可解释性。


基于符号回归的动力学推断方法

推荐语：PySR，DeepMind和普林斯顿等机构联合开发，核心思想围绕遗传编程，性能优异，可自定义函数。
  • Cranmer, M. (2023). Interpretable machine learning for science with PySR and SymbolicRegression. jl. arXiv preprint arXiv:2305.01582.
推荐语：大语言模型用于符号回归，跳出传统的遗传编程思想。将符号回归过程看作将数据“翻译”为表达式的过程，将观测数据进行统一编码，利用Transformer架构学习并输出对应的方程式。
  • Valipour, M., You, B., Panju, M., & Ghodsi, A. (2021). Symbolicgpt: A generative transformer model for symbolic regression. arXiv preprint arXiv:2106.14131.
  • Kamienny, P. A., d’Ascoli, S., Lample, G., & Charton, F. (2022). End-to-end symbolic regression with transformers. Advances in Neural Information Processing Systems, 35, 10269-10281.
推荐语：第一篇结合循环神经网络（Recurrent Neural Network，RNN）和强化学习的深度符号回归（Deep Symbolic Regression，DSR）框架，使用RNN生成可处理的数学表达式分布，并利用强化学习（RL）训练该RNN，更新参数以逼近底层动力学表达式。第二篇为有限表达式方法，基于强化学习找到生成表达式中的最优非线性函数、二进制运算和数值系数组合，用于求解跃迁路径理论(TPT)中的高维问题。
  • Mundhenk, T., Landajuela, M., Glatt, R., Santiago, C. P., & Petersen, B. K. (2021). Symbolic regression via deep reinforcement learning enhanced genetic programming seeding. Advances in Neural Information Processing Systems, 34, 24912-24923.
  • Song, Z., Cameron, M. K., & Yang, H. (2023). A finite expression method for solving high-dimensional committor problems. arXiv preprint arXiv:2306.12268.
推荐语：通过计算规则和符号来解释数学运算和系统状态变量，通过表达式树建立数学公式的符号推理，并使用蒙特卡罗树搜索(MCTS)代理来探索基于测量数据的最优表达式树。
  • Sun, F., Liu, Y., Wang, J. X., & Sun, H. (2022). Symbolic physics learner: Discovering governing equations via monte carlo tree search. arXiv preprint arXiv:2205.13134.
推荐语：提出图结构物理机制的符号学习模型，采用自动搜索的方式从数据中学习物理机制中各关键变量的依赖关系，作为公式骨架，然后使用符号回归方法得到最终描述微观机制的符号公式
  • Shi, H., Ding, J., Cao, Y., Liu, L., & Li, Y. (2022). Learning symbolic models for graph-structured physical mechanism. In The Eleventh International Conference on Learning Representations.


基于基函数的推断方法

推荐语：第一篇是基于非正交函数库从含噪和网络结构缺失的数据中推断复杂网络ODE的框架，第二篇进一步提出基于消息传递机制和非正交函数库的复杂网络SDE推断框架。应用于多套实际观测数据（实验数据），为理解和描述复杂系统动态机制提供框架支撑。
推荐语：基于基函数学习随机过程的力场和扩散项，第一篇主要是方法描述，第二篇描述该方法应用于细胞迁移场景下的动力学学习。
  • Frishman, A., & Ronceray, P. (2020). Learning force fields from stochastic trajectories. Physical Review X, 10(2), 021009.
  • Brückner, D., & Broedersz, C. P. (2024). Learning dynamical models of single and collective cell migration: a review. Reports on Progress in Physics.
推荐语：状态估计是复杂系统预测和控制的基础，本文提出了一种数据驱动的状态估计方法，并且通过基函数对系统动力学进行学习。
  • Course, K., & Nair, P. B. (2023). State estimation of a physical system with unknown governing equations. Nature, 622(7982), 261-267.
推荐语：基于图神经网络的网络结构推断和动力学预测方法。


深度学习预测复杂系统临界点

推荐语：基于GIN-GRU架构，仅通过节点状态的时间序列在早期就实现定量预测各种复杂系统中的临界转折点，并基于模型微调对实际非洲植被生态系统的临界点进行预测。
  • Liu, Z., Zhang, X., Ru, X., Gao, T. T., Moore, J. M., & Yan, G. (2024). Early predictor for the onset of critical transitions in networked dynamical systems. Physical Review X, 14(3), 031009.
推荐语：提出重缩放自动密度（RAD），使得在系统受到未知水平噪声干扰时准确识别临界点附近的时间序列特征。
  • Harris, B., Gollo, L. L., & Fulcher, B. D. (2024). Tracking the distance to criticality in systems with unknown noise. Physical Review X, 14(3), 031021.
推荐语：提出估计朗之万型动力学在白噪声或红噪声驱动下的线性恢复速率变化，用于预测连续、离散及非平稳噪声等场景下的临界点。
  • Morr, A., & Boers, N. (2024). Detection of approaching critical transitions in natural systems driven by red noise. Physical Review X, 14(2), 021037.


跨尺度系统建模

推荐语：基于广义Onsager定理，从随机耗散系统的微观轨迹学习宏观动力学描述，建立具有可解释性的热力学坐标，主要应用在聚合物链的拉伸动力学。
  • Chen, X., Soh, B. W., Ooi, Z. E., Vissol-Gaudin, E., Yu, H., Novoselov, K. S., … & Li, Q. (2024). Constructing custom thermodynamics using deep learning. Nature Computational Science, 4(1), 66-85.
推荐语：基于因果涌现的理论框架，建立多尺度机器学习模型，从微观数据中识别涌现，得到最优的粗粒化策略和宏观动力学，可以增强机器预测的泛化能力。
  • Mingzhe Yang, Zhipeng Wang, Kaiwei Liu, Yingqi Rong, Bing Yuan, Jiang Zhang, Finding emergence in data by maximizing effective information, National Science Review, 2024, nwae279, https://doi.org/10.1093/nsr/nwae279 | 对本工作感兴趣的伙伴可以关注：因果涌现第三季：12.基于数据驱动的多尺度因果涌现框架
推荐语：综述文章，和自由能原理相关，基于层次生成模型和贝叶斯推断学习不同时间尺度上表征神经元活动。
  • Medrano, J., Friston, K., & Zeidman, P. (2024). Linking fast and slow: The case for generative models. Network Neuroscience, 8(1), 24-43.
对自由能原理感兴趣的伙伴可以关注自由能原理与强化学习读书会，其中第六期为Karl Friston的分享《意识的物理学——主动推理的顶层逻辑》。

模块四：应用-超材料设计和城市系统

当我们对复杂系统的机制有了充分的了解和认识，就能够更好的对系统进行控制和反向设计。
所以通过前三个模块的探讨，我们第四个模块，将以材料领域和城市领域为例，重点介绍如何通过生成建模和人工智能技术，识别和重构复杂系统中的网络结构和因果关系，并在实际应用中优化系统设计。

基于人工智能的结构反向设计：以超材料为例

推荐语：了解力学超材料基本概念，以超材料反向设计为例，介绍基于人工智能的结构（或更一般的物理场）反向设计三种基本方法及各自特点：（1）正向预测网络+优化；（2）可逆神经网络（invertible neural networks及衍生diffusion model）；（3）直接逆神经网络：串联构造。
  • Deng, B., Zareei, A., Ding, X., Weaver, J. C., Rycroft, C. H., & Bertoldi, K. (2022). Inverse design of mechanical metamaterials with target nonlinear response via a neural accelerated evolution strategy. Advanced Materials, 34(41), 2206238.
  • Bastek, J. H., & Kochmann, D. M. (2023). Inverse design of nonlinear mechanical metamaterials via video denoising diffusion models. Nature Machine Intelligence, 5(12), 1466-1475.
  • Ha, C. S., Yao, D., Xu, Z., Liu, C., Liu, H., Elkins, D., … & Zheng, X. (2023). Rapid inverse design of metamaterials based on prescribed mechanical behavior through machine learning. Nature Communications, 14(1), 5765.
  • 于相龙，周济著.力学超材料的构筑与超常性能[M].合肥：中国科学技术大学出版社,2021
  • Mao, Y., He, Q., & Zhao, X. (2020). Designing complex architectured materials with generative adversarial networks. Science advances, 6(17), eaaz4169.
  • Liu, Z., Zhu, D., Rodrigues, S. P., Lee, K. T., & Cai, W. (2018). Generative model for the inverse design of metasurfaces. Nano letters, 18(10), 6570-6576.
  • Zheng, L., Karapiperis, K., Kumar, S., & Kochmann, D. M. (2023). Unifying the design space and optimizing linear and nonlinear truss metamaterials by generative modeling. Nature Communications, 14(1), 7563.
  • Wang, L., Chan, Y. C., Ahmed, F., Liu, Z., Zhu, P., & Chen, W. (2020). Deep generative modeling for mechanistic-based learning and design of metamaterial systems. Computer Methods in Applied Mechanics and Engineering, 372, 113377.
  • Bastek, J. H., Kumar, S., Telgen, B., Glaesener, R. N., & Kochmann, D. M. (2022). Inverting the structure–property map of truss metamaterials by deep learning. Proceedings of the National Academy of Sciences, 119(1), e2111505119.


城市系统的自动建模

推荐语：城市也是多尺度的复杂系统，现实世界积累的海量真实数据使其成为复杂系统自动建模方法的理想应用场景。本节推荐的参考文章涵盖城市复杂系统的三类主要问题（详见第一篇综述文章）。

  • Ding, J., Liu, C., Zheng, Y., Zhang, Y., Yu, Z., Li, R., … & Li, Y. (2024). Artificial Intelligence for Complex Network: Potential, Methodology and Application. arXiv preprint arXiv:2402.16887.

预测和模拟：预测复杂系统的长期演化状态、韧性对于城市中的基础设施、生态系统至关重要，下列文献综合利用了前述提到的物理知识引导神经网络(PINN)、神经常微分方程(Neural ODE)以及扩散模型(Diffusion Generative Model)技术来克服基于真实数据的建模难题。

  • Li, R., Wang, H., & Li, Y. (2023). Learning slow and fast system dynamics via automatic separation of time scales. In Proceedings of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (pp. 4380-4390).

  • Li, R., Wang, H., Piao, J., Liao, Q., Li, Y. (2024). Predicting Long-term Dynamics of Complex Networks via Identifying Skeleton in Hyperbolic Space. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining.

  • Liu, C., Ding, J., Song, Y., Li, Y. (2024). TDNetGen: Empowering Complex Network Resilience Prediction with Generative Augmentation of Topology and Dynamics. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining.

  • Chen, H., Ding, J., Li, Y., Wang, Y., & Zhang, X. P. (2024). Social physics informed diffusion model for crowd simulation. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 38, No. 1, pp. 474-482).

  • Li, J., Wang, H., Chen, X. (2024). Physics-informed Neural ODE for Post-disaster Mobility Recovery. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining.

控制和优化：城市基础设施的攻击与防护是一类经典的复杂系统控制优化应用，传统的组合优化方法面临解空间巨大、搜索低效问题，数据驱动的强化学习方法具有显著的优势（下面第一篇），近期研究表明大语言模型也可用于启发式的求解这类问题（下面第二篇）。

  • Mao, J., Cao, L., Gao, C., Wang, H., Fan, H., Jin, D., & Li, Y. (2023). Detecting vulnerable nodes in urban infrastructure interdependent network. In Proceedings of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (pp. 4617-4627).

  • Mao, J., Zou, D., Sheng, L., Liu, S., Gao, C., Wang, Y., & Li, Y. (2024). Identify Critical Nodes in Complex Network with Large Language Models. arXiv preprint arXiv:2403.03962.

规律发现：基于真实数据，利用前述复杂系统的动力学推断方法能够发现城市系统的内在演化规律，以人流移动为例，相比经典的“社会力”物理模型(Social Force)，基于真实数据提炼的新物理公式能更好的模拟各种场景下的人群移动。

  • Shi, H., Ding, J., Cao, Y., Liu, L., & Li, Y. (2022). Learning symbolic models for graph-structured physical mechanism. In The Eleventh International Conference on Learning Representations.

  • Zhang, G., Yu, Z., Jin, D., & Li, Y. (2022). Physics-infused machine learning for crowd simulation. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (pp. 2439-2449).




点击“阅读原文”，报名读书会