导语


理解阻塞相变的物理本质是统计物理中有挑战性的问题。甚至其中的一些基本问题，例如它究竟是一阶相变还是二阶相变，都一直存在争议。近期关于系统的有限尺寸标度研究发现，在准静态加载的条件下，阻塞相变既不是普通的一阶相变，也不是普通的二阶相变，而是一种无序一阶相变。


关键词：非平衡态，无序系统，阻塞相变，标度行为

邓越、潘登、金瑜亮 | 作者

中国物理学会期刊网，选自《物理》2024年第10期 | 来源





1. 阻塞相变背景介绍




在颗粒物质、胶体、泡沫、细胞等无序非平衡体系中，从流体态到非晶固态的转变过程被称为“阻塞相变”[1—8]。这类体系粒子之间的相互作用能量比热运动能量高很多个数量级，因此可以等效地认为处于零温状态。不同于常见的液固相变，阻塞相变是由于体积分数 (而非温度) 变化导致的，是一种非平衡相变。当体积分数超过阻塞相变体积分数φJ时，粒子间由于相互接触形成稳定的力学网络，从而成为固态 (图1)。在快速压缩的过程中，三维 (单分散) 体系的φJ≈0.64[9]，而二维 (双分散) 体系的φJ≈0.84[10]。近年来的研究发现，φJ还会和压缩速率等制备过程相关[11]。阻塞相变前后体系的结构都是无序的，明显不同于液体的结晶过程。


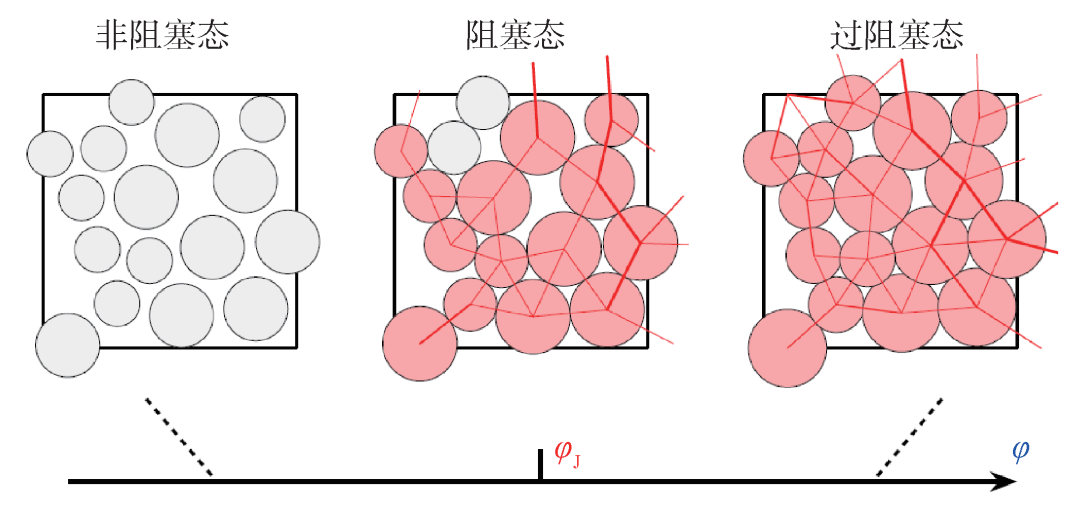
图1 阻塞相变示意图，展示了三种状态下典型的粒子构型和相互作用力网


理解阻塞相变的物理本质是统计物理中有挑战性的问题。甚至其中的一些基本问题，例如它究竟是一阶相变还是二阶相变，都一直存在争议。在阻塞相变附近，体系似乎同时具有一阶和二阶相变的特征。在准静态压缩或剪切的过程中，作为序参量的粒子平均配位数 (平均接触数) Z 在φJ处不连续地从Z=0 跳跃到Ziso=2d，其中Ziso=2d 是d 维空间具有刚性的最小配位数，称为等静定 (isostatic) 配位数——从这一角度，阻塞相变具有一阶相变的典型特征。另一方面，阻塞相变也呈现二阶相变的特征，体现为如下多种发散的长度尺度。(1)由过剩接触数ΔZ=Z–Ziso决定的等静定关联长度随体系趋近于相变点而发散，l*~ΔZ -1~(φ–φJ)-1/2 [12,13]。当体系的尺度小于l*时，边界上的力学扰动将导致失稳。(2)在φJ处，单粒子接触数Zi 的空间分布具有超均匀性 (空间密度涨落小于随机分布的情形) [14，15]，其对应的超均匀关联长度在相变点发散，ξH~ΔZ –νH (其中νH为对应的指标)。(3)在阻塞相变发生前，体系处于全阶复本对称破缺 (微观构型组成的相空间具有分形结构) 的Gardner相[16，17]。Gardner相的临界性也在阻塞相变中体现，即粒子的笼振动动力学 (caging vibrational dynamics) 行为具有长程关联，对应了发散的笼关联长度，ξG∼∞。(4)在流变学模拟中，非阻塞流体的黏度在趋近相变点的过程中发散，对应了发散的流变学关联长度，ξR~(φJ–φ)–ν，其中ν=1[18]。


为了澄清阻塞相变的物理本质，有限尺寸的标度分析尤为重要。近期，我们通过系统的有限尺寸标度研究发现，在准静态加载的条件下，阻塞相变既不是普通的一阶相变，也不是普通的二阶相变，而是一种无序一阶相变 (first-order transition with quenched disorder) [19]。





2. 无序一阶相变及其标度行为




平衡态体系符合涨落耗散定理。例如，在伊辛模型中，表征涨落的非连接磁化率χdis=N(<m2>-<m>2)和表征响应的连接磁化率χcon=d<m>/dh 相等，χdis=χcon=χ，其中m为磁化强度 (序参量)，h为外磁场，N为自旋数 (体系大小)。有限尺寸标度理论给出，在二阶相变处χ~Nγ/(dν)，其中γ和ν都是临界指标；而在一阶相变处，χ~N [20]。

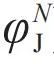上述有限尺寸标度在零温 (或低温) 无序体系中不再成立。当温度足够低时，无序涨落的影响超过了热涨落，涨落耗散定理不再满足。在有限大体系中，相变点本身 (如阻塞相变的) 由于无序的存在而有一个分布ρ(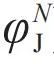)，从而改变了有限尺寸标度。这类体系的一阶相变称为“无序一阶相变”。在无序一阶相变附近，非连接磁化率和连接磁化率满足标度关系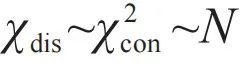，。这一特有的有限尺寸标度行为是区别无序一阶相变和标准一阶或二阶相变的重要依据。研究无序一阶相变最经典的模型是随机场伊辛模型。在该模型中，每个格点上的外场hi 是一个满足给定分布的随机数，且不随着时间变化。近年来的研究发现，超稳玻璃的脆性屈服[21]和熔化[22]也可能属于无序一阶相变。




3. 零温准静态加载下的阻塞相变

是无序一阶相变




从统计物理的角度研究阻塞相变的性质，首先需要定义一个统计系综。在文献[19]的颗粒模型模拟工作中，我们首先用无热准静态循环剪切的方法制备了一个非平衡统计系综。在不同的体积分数φ以及循环强度(最大应变)γmax下，经过多次循环后，体系会“吸收”到一个固定的构型 (称为可逆相)，或者在不同构型间持续演化(称为不可逆相)，如图2(a)所示。在不可逆相中，每次循环结束后收集样本，发现粒子的轨迹呈现类似扩散运动的行为，如图2(b)所示。这意味着即使在零温状态下，通过循环剪切这种外力加载的方式，非平衡颗粒系统也可以有效地遍历相空间，从而定义一个统计系综。更细致的分析发现，这一系综中包括了四种状态，除了前文提到的非阻塞态、(过) 阻塞态，还存在部分结晶态和易碎态 (fragile state)，如图2(c)所示。其中阻塞态和易碎态的区别在于，前者存在所有方向都发生渝渗的力网，而后者的力网只在单一方向发生渝渗。力学稳定性分析发现，部分结晶态和易碎态在力学微扰下会变成非阻塞态。这意味着在严格的准静态极限下 (剪切速率严格趋于零) ，该系综只会包括非阻塞态和阻塞态，其概率分布如2(d)所示。


图2 (a)颗粒物质无热准静态剪切相图；(b)不可逆相中的粒子轨迹(插图为均方位移，实线代表均方位移和时间成正比的扩散行为)；(c)四种典型的构型；(d)二维阻塞相变附近(φ≈0.844)配位数的概率分布(所有部分结晶态和易碎态都统计为非阻塞态)


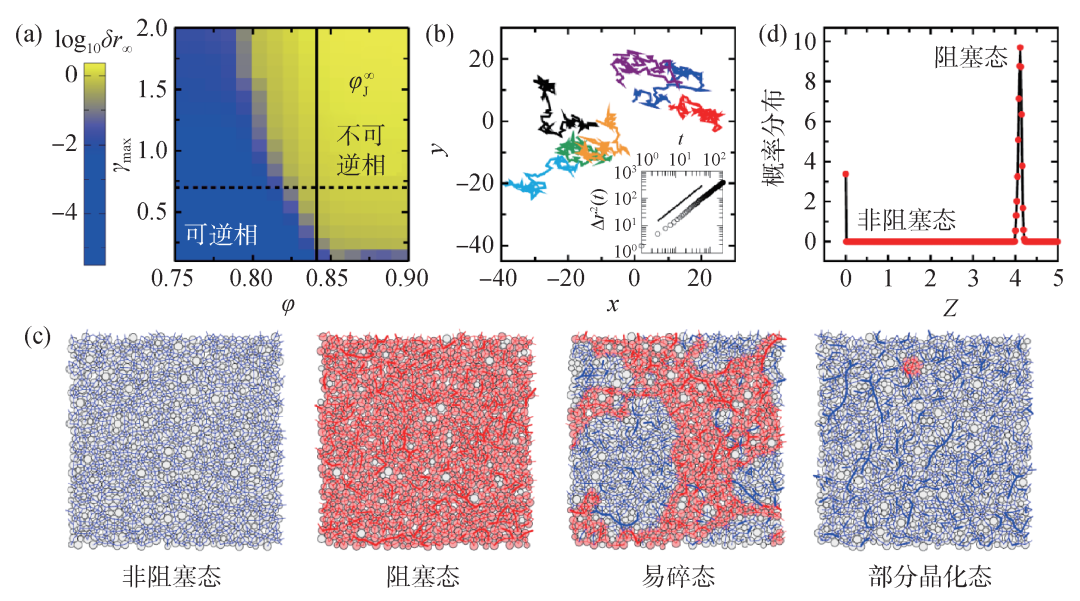
上述统计系综的非连接磁化率χdis和连接磁化率χcon满足一定的有限尺寸标度，如图3(a)，(b)所示，即χdis/N和χcon/N1/2都可以写成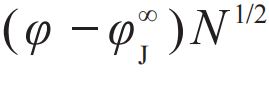的函数，其中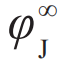为热力学极限下的阻塞相变密度，N为粒子数。模拟数据与假设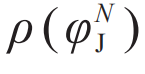为高斯分布推导的磁化率理论结果一致。特别是，在阻塞相变附近 (图3(c)的极小值)，磁化率具有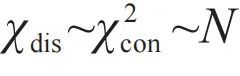的标度行为，从而为阻塞相变是无序一阶相变的观点提供了直接的证据。无序一阶相变理论也可以解释先前报道的快速压缩淬火系综的数据[23]。因此，在无热 (无序涨落主导)、准静态加载 (不存在部分结晶态、易碎态等不稳定瞬态) 的条件下，阻塞相变是无序一阶相变的结论可能具有普遍性。


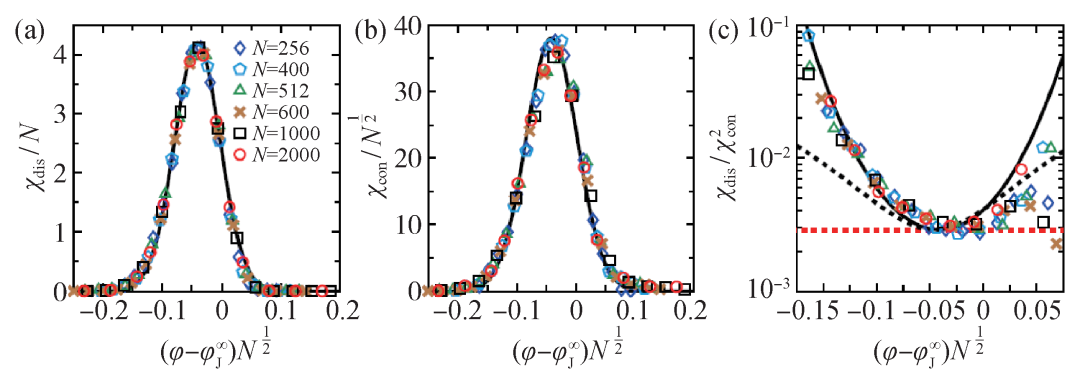
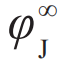图3 阻塞相变的磁化率   (a)非连接磁化率χdis；(b)连接磁化率χcon；(c)χdis/χcon2的有限尺度标度行为。其中为热力学极限下的阻塞相变体积分数。黑色实线为理论值，黑色虚线和红色虚线分别表示在极值附近的零阶近似和最低阶展开理论结果





4. 展望




除了颗粒体系，无序一阶相变也可能出现在其他非平衡体系，如活性物质等。该研究为理解液体和非晶固体之间的转变提供了新的视角，凸显了无序的存在可以改变标准相变的标度率，其方法有望拓展到其他无序非平衡相变的研究。

致 谢   感谢中国科学院理论物理研究所的高性能计算平台的支持。


参考文献

[1] Liu A J，Nagel S R. Nature，1998，396：21
[2] Torquato S，Stillinger F H. Reviews of Modern Physics，2010，82：2633
[3] van Hecke M. J. Phys. Condens. Matter，2010，22：033101
[4] Liu A J，Nagel S R. Annual Review of Condensed Matter Physics，2010，1(1)：347
[5] Baule A，Morone F，Herrmann H J et al. Reviews of Modern Physics，2018，90：015006
[6] Charbonneau P，Kurchan J，Parisi G et al. Annual Review of Condensed Matter Physics，2017，8：265
[7] Behringer R P，Chakraborty B. Reports on Progress in Physics，2018，82：012601
[8] Pan D，Wang Y，Yoshino H et al. Physics Reports，2023，1038：1
[9] Makse H A，Johnson D L，Schwartz L M. Phys. Rev. Lett.，2000，84：4160
[10] O′hern C S，Silbert L E，Liu A J et al. Phys. Rev. E，2003，68：011306
[11] Chaudhuri P，Berthier L，Sastry S. Phys. Rev. Lett.，2010，104：165701
[12] Wyart M，Nagel S R，Witten TA. Europhysics Letters，2005，72：486
[13] Silbert L E，Liu A J，Nagel S R. Phys. Rev. Lett.，2005，95：098301
[14] Hexner D，Liu A J，Nagel S R. Phys. Rev. Lett.，2018，121：115501
[15] Hexner D，Urbani P，Zamponi F. Phys. Rev. Lett.，2019，123：068003
[16] Charbonneau P，Kurchan J，Parisi G et al. Nat. Commun.，2014，5：3725
[17] Berthier L，Charbonneau P，Jin Y et al. Proc. Natl. Acad. Sci.USA，2016，113：8397
[18] Olsson P，Teitel S. Phys. Rev. Lett.，2007，99：178001
[19] Deng Y，Pan D，Jin Y. Nat. Commun.，2024，15：7072
[20] Binder K. Ferroelectrics，1987，73：43
[21] Ozawa M，Berthier L，Biroli G et al. Proc. Natl. Acad. Sci. USA，2018，115：6656
[22] Zhang K，Li X，Jin Y et al. Soft Matter，2022，18：6270
[23] O′Hern C S，Langer S A，Liu A J et al. Phys. Rev. Lett.，2002，88：075507


参考文献可上下滑动查看



作者简介

邓越 (中国科学院理论物理研究所、中国科学院大学物理科学学院)

潘登 (中国科学院理论物理研究所)

金瑜亮 (中国科学院理论物理研究所、中国科学院大学物理科学学院、国科温州研究院)


非平衡统计物理读书会启动！


2024年诺贝尔物理学奖授予人工神经网络，这是一场统计物理引发的机器学习革命。统计物理学不仅能解释热学现象，还能帮助我们理解从微观粒子到宏观宇宙的各个层级如何联系起来，复杂现象如何涌现。它通过研究大量粒子的集体行为，成功地将微观世界的随机性与宏观世界的确定性联系起来，为我们理解自然界提供了强大的工具，也为机器学习和人工智能领域的发展提供了重要推动力。


为了深入探索统计物理前沿进展，集智俱乐部联合纽约州立大学石溪分校教授汪劲、德累斯顿系统生物学中心博士后研究员梁师翎、香港浸会大学助理教授唐乾元（傅渥成），共同发起「非平衡统计物理」读书会，关注非平衡统计物理的前沿理论、生命和热力学、统计物理与机器学习交叉三个大的主题方向，涵盖热机优化问题、涨落相关的热力学、反常热力学现象、信息视角下的热力学、生命系统的景观和流理论、活性物质、生命系统、种群动力学、机器学习和人工智能等前沿话题。我们诚挚邀请相关领域的研究者分享工作，也欢迎感兴趣的朋友们一起参与讨论交流！（扫描下图中二维码报名）




推荐阅读
1. 诺奖得主 Parisi 最新 Nature 速递：二维伊辛自旋玻璃的量子相变
2. 百年“伊辛模型”新探索：模拟量子相变新方法
3. Nat.Commun.前沿：变分自回归网络求解非平衡态统计力学和动力学相变
4. 张江：第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程
5. 龙年大运起，学习正当时！解锁集智全站内容，开启新年学习计划

6. 加入集智，一起复杂！



点击“阅读原文”，报名读书会