从抛硬币到相互绕转的双黑洞系统,再到生物体中的基因开关,许多物理系统都具有多重结果,这种复杂性限制了我们对系统的预测能力。这篇发表于 Physics Today 的科普文章介绍了非线性动力学中的多稳定性。任何由初始条件决定,且具有多个稳定结果的系统被称为多稳定系统。
研究领域:非线性动力学,多稳定性,混沌,吸引子,分形
Álvar Daza, Alexandre Wagemakers, Miguel A. F. Sanjuán | 作者
彭晨 | 译者
梁金 | 审校
文章题目:Multistability and unpredictability
文章地址:https://pubs.aip.org/physicstoday/article/77/11/44/3318349/Multistability-and-unpredictabilityIn-numerous
做决定有时很难。将决定权交给一个公正的权威方,比如硬币或骰子,可能有助于缓解压力。事实上,只需要几美元,你就可以买到一个决策玩具(见图1),它由一根刚性杆,和标有“是”“否”“可能”的三个磁铁组成。只要把杆拉离平衡状态,让它不规律地摆动,最终指向的答案就是钟摆为你做出的决策。
图1. 决策钟摆玩具有三种可能的结果:是、否和可能。摆中的磁体最有可能停在三个磁体之一的正上方。初始条件和多个最终停靠的位置之间有复杂的相互作用,使钟摆成为一个多稳定性系统。钟摆给出的最终答案看似是随机的,实际上,这个系统可以用分别代表三个答案的吸引域(彩色部分)来建模,初始释放点将决定最终的停靠点。
然而,当应用一点物理推理时,问题就出现了。考虑磁体和磁棒之间的吸引力,可以很容易地推导出钟摆的运动方程[1]。给定初始条件,这些确定性方程将精确地预测钟摆的最终位置。因此,实际上你才是做决定的人,最终结果都基于你对初始状态的选择!你可以让杆在你想要的结果附近释放,但这感觉太像作弊了。那么,你对最终结果实际有多大的控制权呢?
这是一个有趣的数学问题,但这些原理不仅仅适用于决策玩具。任何由初始条件决定,且具有多个稳定结果的系统被称为多稳定系统(multistable system)。这类系统通常用非线性运动方程建模,并用数值方法求解。然而,混沌系统初始条件的极小误差,即使是由有限的数值精度导致的,也会导致显著不同的结果,例如,掷骰子或硬币的运动可以用经典力学来描述[2],但确切的初始条件很大程度上会影响最终的稳定结果。正因如此,统计学教科书经常使用掷骰子或硬币作为随机性的例子。
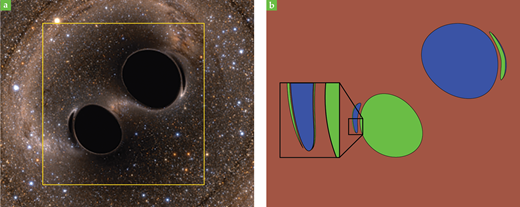
多稳定性存在于物理学的诸多领域,从量子世界到广义相对论,涵盖基本概率到复杂大气模型。的确,爱因斯坦场方程中固有的非线性常常导致多稳定性的情况[3]。例如,当两个黑洞相互绕转,它们周围的光路由于相互竞争的引力阱而变得复杂,且难以预测。在图2所示的情况下,光子面临三种可能的结果:被黑洞1吸收,被黑洞2吸收,或者逃逸。虽然双黑洞周围的光子与磁钟摆有很大不同,但这两个系统有一些共同的特征。
图2. 双黑洞构成了一个多稳定系统,如仿真图 (a) 所示(来源:Courtesy of the Simulating eXtreme Spacetimes project.)。它们可以用不同的吸引域来表示 (b),在这个系统附近的光子有三种可能的最终状态:被第一个黑洞捕获(蓝色),被第二个黑洞捕获(绿色),或者逃逸。在图中放大的“眉毛”状狭窄区域,距离较远的黑洞引力比近处的黑洞更大。一些模型预测发现“眉毛”区域具有分形层次,这增加了预测的复杂性。
多稳定系统也出现在其他科学学科中。基因开关(genetic toggle switch)是一种基因调控机制,即蛋白质的初始浓度决定基因倾向于表达还是沉默状态[4]。这种简单的基序可以构建出复杂的调控网络,分析系统的多稳定性有助于更好地理解基因表达。
系统渐近的状态并不局限于稳态,一些复杂情况中可能包括周期性甚至混沌轨道,例如,摆钟的多稳定解对应的是不同模式的振荡 [5]。图3显示了调制激光的脉冲模式,这些模式依赖于初始条件[6]。一般来说,如果系统任何性质允许我们区分出不同的渐近状态,那么就可以应用多稳定性的理论框架 [7]。
图3. 当设置不同的初始条件时,调制激光器表现出多稳定性[6]。上图中,初始条件导致输出脉冲的功率(红色)为调制信号(蓝色)的三分之一。而下图中,输出脉冲和调制信号具有相同的频率。
研究多稳定系统行为的一种方法是建立将初始条件与最终结果之间的关联图,这个图被称为吸引域(basin of attraction)。例如,在图1中,如果决策钟摆从黄色吸引域中释放,它最终也将停在黄色区域上方。这个术语是从水文学中借用来的,水文学中的流域是指,雨水最终聚集形成的特定水体所在的土地区域。非线性系统中,固有的不可预测性常常导致复杂的,有时甚至是分形的吸引域形状。下图展示了各种精美的吸引域。
当吸引域具有分形边界时,认为结果可预测的一般直觉是错误的[8],这就是为什么决策钟摆这样的系统看起来是随机的。在具有平滑吸引域边界的系统中,初始条件的精度提高10倍,系统的总体可预测性相应提高10倍。对于分形吸引域,将精度提高10倍可能只会导致预测精度提高2-3倍,或在极端情况下不会提高。由于分形的自相似性,这种情况在每个尺度上都会重复出现。
分形因其在所有尺度上的复杂结构和非整数维度而得名(见下框中介绍)。传统拓扑维度可以理解为,确定物体内一个点的位置所需的坐标数量:一个坐标可以定义曲线上的位置,两个坐标可以定义曲面上的点,诸如此类。分形维数推广了这个概念,并提供了对物体占据空间的广泛程度的信息。例如,一条分形维数为1.53的平面曲线所占的空间比直线大,但比二维表面小。这个数字表示我们离那些极限情况有多近。
尽管如此,分形边界的特性不仅限于自相似性和非整数维度。它们只是冰山一角,因为大量分形吸引域涵盖了具有基本预测意义的非凡现象。
分形维数
维度的概念比学校里教的要复杂得多,维度计算可以使用一种称为盒计数法(box-counting method)的构造方法。做法是在感兴趣的集合上覆盖边长为ε的盒子,并计算含有集合部分的盒子数量 N(ε)。使用一组递减的ε值重复该过程,N(ε) 的值期望随着ε的减小而增大。而事实上,对于较小的ε, N(ε) 与 ε-d成正比,其中d是集合的盒计数,即分形维数。
对于简单的欧几里得集合,如线段和圆盘,盒计数法似乎是不必要的,因为它们的维度是已知的,即1表示线段,2表示圆盘。对于像分形这样复杂的几何对象,盒计数法变得非常有用。
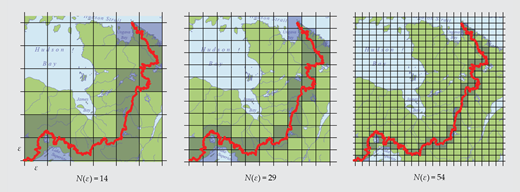
分形是具有非整数维度的几何学复杂集合。一个分形例子是哈德逊湾和大西洋流域之间的边界,不同地理位置的排水最终会进入不同流域,类似于动力系统中结果对初始条件的敏感依赖。
这几张地图说明了盒计数法在流域边界(红色部分)的应用。每次我们将分辨率提高一倍,覆盖曲线的盒子(灰色部分)的数量就会增加。继续这一过程,直到ε值非常小,我们可以找到一个标度律 (scaling law),其中ε值的指数幂给出了曲线的分形维数。
一般来说,分形的分形维数大于其拓扑维数(对于直线为1),但小于其嵌入的空间维数(对于曲面为2)。多稳定系统通常呈现出具有分形边界的吸引域,对系统的可预测性具有根本性的影响。
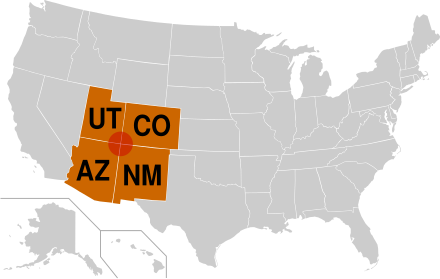
通常,边界将两个区域分开,比如国界。有时,孤立的点分隔了两个以上的地区,例如,四角(Four Corners)是亚利桑那州、犹他州、科罗拉多州和新墨西哥州之间的分界点。这样的点具有更高的不可预测性,偏离确切的边界点可能导向两种以上的可能结果,例如,在四角处被推倒的人可能倒向四个州的任何一个。当边界完全由这些点组成时会发生什么?尽管这样的边界有些难以想象,但分形物体经常挑战传统的理解。
Four Corners|图片来源:https://en.wikipedia.org/wiki/Four_Corners
20世纪初,日本拓扑学家 Takeo Wada 提出了一种创造这种结构的方法:共享同一边界的三个相连集合。后来以他的名字命名为 Wada 域(Wada basin),表示被单一边界分隔的三个或多个分形域。这种拓扑特性并不少见,甚至在简单的系统中也很常见,例如在连续受迫作用下的阻尼摆[8]。
Wada 域的牛顿分形例子。|图片来源:https://en.wikipedia.org/wiki/Lakes_of_Wada
Wada 域并不是最不可预测。还有一些分形曲线,如皮亚诺曲线和希尔伯特曲线,可以占据整个空间。一个占据全部空间的边界,意味着初始位置最微小的不确定性将导致完全未知的结果。尽管是确定性的,但无论精度如何提高,系统总是无法预测的。这样的情境是由 riddled 域模拟,某种程度上,riddled 域可以被认为是确定性和随机性之间的桥梁。此外,多稳定性系统还有许多更奇特的例子,包括零星分形域、混合域和有触角的域[9]。
通常来说,分析动态过程的第一步包括让状态演变到可以识别出渐近行为。例如,决策钟摆释放后一段时间,最终停在哪个结果的态势逐渐明晰,在结果附近仍会保持轻微摆动。当然不同初始条件下的试验可能会发现不同的结果。然而,在一些系统中,这一过程远非显而易见,因为系统的吸引域可能是隐藏的[10]。当吸引域距离相应的结果较远,并且没有导向域的瞬态过程时,就会出现这种情况。探测这种难以捉摸的吸引域需要特殊处理。
当这些吸引子无处不在时,吸引域很靠近其对应的吸引子也会出现问题。当保守混沌与小耗散结合时,会产生极端多稳定性[11],导致产生大量不同的吸引子。事实上,这种情况可以产生任意数量的吸引子。此外,对系统的人为操作可以定制多稳定性场景,两个特殊的例子是超稳定性(megastability)[12]和嵌套稳定性(matryoshka multistability)[13],嵌套稳定性指吸引子嵌套形成洋葱状结构。
此外,改变研究对象的参数有时会产生两种可能的结果,这一现象称为分岔(bifurcation)。同一个系统可能呈现出各种各样的情况,这取决于它的具体参数。域和相关现象的丰富多样性,使得创建工具理解不可预测性并进行分类很有必要。
量化吸引域不可预测性的最直接方法是测量相对体积。考虑一个灌铅的骰子,其中一个面的吸引域体积是其他面的体积总和的20倍。显然,大多数时候,骰子落地时这个偏置的面会朝上。这种被称为域稳定性(basin stability)的简单测量方法[14]已经成功地应用于描述多稳定网络和高维系统(如大气模式)。
但是域不仅只有大小。两个系统中吸引域体积相同,不一定意味着两者的可预测性相同。体积之外,吸引域的形态也很重要。例如,一个由平滑边界分隔的具有对称域的双稳态系统(想象一个 2×2 的棋盘)和一个有混乱边界(想象电视噪声)的系统可以呈现相同的体积。尽管两种情况下的吸引域稳定性是相同的,但情况却大不相同。吸引域熵(basin entropy)是最近开发的一种工具,它结合了这两个方面来度量不确定性[15]。
吸引域熵可以理解为多个因素的非线性组合,包括边界的分形维数和吸引域内吸引子的数量。这样,熵解释了域的形态,并创建了一个合理的分类[16]。例如,Wada 域使得被边界分隔的吸引子数量最大化,而 riddled 域最大化的是分形维数。除了量化多稳定系统的渐近不可预测性外,吸引域熵还量化分形边界、分岔和其他特征。
然而,我们并非只能观察多稳定系统的复杂性,还可以试着利用它[17]。有时你发现自己困在一种状态中,很想过渡到另一种状态。这种情况下,确定将系统移出吸引域所需的最小扰动是至关重要的。有趣的是,这种最小作用提供了吸引域有关的敏感性的另一种衡量标准。摒弃静态方法,可以使用一个精确时控的扰动,驱动从一个渐近状态到另一个渐近状态的演化。无论采用何种方法,一旦确定了最佳扰动窗口,外部控制就可以使系统达到想要的状态。最佳的扰动可能不是先验的,或者使用一些反馈方法来避开这个困难。
深入研究多稳定性改变了我们对日常事物的看法,并揭示了一个充满新可能性的世界。本文的讨论起始于一个小小的决策玩具,但对多稳定性的理解在神经科学等高级主题中也至关重要[18]。通过利用从非线性动力学研究中衍生出来的词汇,类似于控制简单钟摆的运动方程,我们可以更深入地理解认知决策背后的复杂机制。多稳定系统中吸引子间的相互作用反映了个体做出决策时复杂的认知过程。
多稳定性是物理学各个领域都普遍观察到的现象,包括经典力学,量子力学和宇宙学,体现了它在揭示不同尺度和领域物理现象复杂性方面的重要性。从基本动力系统的研究中获得的见解通常对解决在不同领域遇到的挑战具有深远的影响。简单系统中的经验提供了有价值的视角和方法论,为物理学中存在已久的问题提供了新的洞见。因此,对多稳定性的探索不仅丰富了我们对基础物理的理解,也促进了跨学科的协同作用。
参考文献
1. A. E. Motter et al., Phys. Rev. Lett. 111, 194101 (2013).
2. J. Strzałko et al., Dynamics of Gambling: Origins of Randomness in Mechanical Systems, Springer (2009).
3. A. Daza et al., Phys. Rev. D 98, 084050 (2018).
4. U. Alon, An Introduction to Systems Biology: Design Principles of Biological Circuits, 2nd ed., CRC Press (2020).
5. T. Burzynski, P. Perlikowski, P. Brzeski, Chaos 34, 021104 (2024).
6. A. N. Pisarchik, U. Feudel, Phys. Rep. 540, 167 (2014).
7. A. N. Pisarchik, A. E. Hramov, Multistability in Physical and Living Systems: Characterization and Applications, Springer (2022).
8. J. Aguirre, R. L. Viana, M. A. F. Sanjuán, Rev. Mod. Phys. 81, 333 (2009).
9. Y. Zhang, S. H. Strogatz, Phys. Rev. Lett. 127, 194101 (2021).
10. D. Dudkowski et al., Phys. Rep. 637, 1 (2016).
11. C. Hens, S. K. Dana, U. Feudel, Chaos 25, 053112 (2015).
12. J. C. Sprott et al., Eur. Phys. J. Spec. Top. 226, 1979 (2017).
13. A. Karimov et al., Chaos Solitons Fract. 187, 115412 (2024).
14. P. J. Menck et al., Nat. Phys. 9, 89 (2013).
15. A. Daza et al., Sci. Rep. 6, 31416 (2016).
16. A. Daza, A. Wagemakers, M. A. F. Sanjuán, Chaos Solitons Fract. 159, 112112 (2022).
17. L. Halekotte, U. Feudel, Sci. Rep. 10, 11783 (2020).
18. J. A. S. Kelso, Philos. Trans. R. Soc. B 367, 906 (2012).
集智学园特别策划混沌科学系列课程,带领学员走近混沌理论,理解各类混沌系统,并尝试跨学科应用。课程邀请9位从事混沌及相关跨学科研究的资深学者担任导师,导师团队由著名混沌理论学者、香港城市大学讲席教授、欧洲科学院院士陈关荣领衔。系列课程已经完整上线,加入即可解锁全部课程录播,更有导师们梳理好的系列资料推荐。欢迎对混沌科学和相关理论感兴趣的朋友加入!
![]()
6. 加入集智,一起复杂!
点击“阅读原文”,报名课程