集智俱乐部联合西湖大学理学院及交叉科学中心讲席教授汤雷翰、纽约州立大学石溪分校化学和物理学系教授汪劲、德累斯顿系统生物学中心博士后研究员梁师翎、香港浸会大学物理系助理教授唐乾元,以及多位国内外知名学者共同发起「非平衡统计物理」读书会。本读书会旨在探讨统计物理学的最新理论突破,统计物理在复杂系统和生命科学中的应用,以及与机器学习等前沿领域的交叉研究。
为什么神经网络能够学习?为什么生命系统能够实现自组织和进化?信息如何成为生命过程的重要组成部分?信息和能量之间有怎样的深刻关系?从宏观进入微观,热力学定律仍然保持不变吗?从相变预测到量子多体系统模拟,机器学习如何改变统计物理研究?从神经网络的能量景观到深度学习中的相变现象,统计物理学为理解和改进机器学习算法提供怎样的启发?「非平衡统计物理」读书会将带领大家一起探索这些有趣而深刻的问题。读书会计划从12月12日开始,每周四晚19:00-21:00进行,持续时间预计12周。无论你是致力于突破 AI 算法瓶颈的研究者,探索生命奥秘的科学工作者,还是对复杂系统满怀好奇的探索者,我们诚挚邀请各位朋友参与讨论交流,一起探索爱因斯坦眼中的普适理论!
2024年诺贝尔物理学奖授予 John Hopfield 和 Geoffrey Hinton,表彰他们“通过人工神经网络实现机器学习的基础性发现和发明”,人工神经网络可以说是统计物理引发的机器学习革命。统计物理与机器学习两者之间相互促进:从相变预测到量子多体系统模拟,机器学习深刻地改变了统计物理研究;从神经网络的能量景观到深度学习中的相变现象,统计物理学则为理解和改进机器学习算法提供了独特的视角。
爱因斯坦曾这样评价热力学(统计物理学):“它是唯一一个具有普适性的物理理论,我确信,在其基本概念的适用范围内,它永远不会被推翻。”这一评价深刻揭示了热力学和统计物理在定量描述系统宏观特性及与环境互动中的核心地位。
统计物理学诞生于19世纪,是为了解释热现象而发展起来的物理学分支。它通过研究大量粒子的集体行为,成功地在微观世界的随机性与宏观世界的确定性之间架起桥梁,帮助我们理解从微观粒子到宏观宇宙的各个层级如何联系起来,复杂的现象如何涌现,也为机器学习和人工智能领域的发展提供了重要推动力。在过去几十年里,统计物理学的应用范围已经远远超出了其最初的领域:
-
在理论前沿,研究者们正在重新审视经典热力学,用现代的视角来理解和扩展传统概念,将统计物理从宏观的观测量扩展到介观涨落的统计,以及更小尺度的量子统计物理。
-
在生命科学领域,统计物理学为理解复杂的生物过程提供了新的视角。从细胞内的分子马达到大脑神经网络,统计物理方法正在帮助我们揭示生命的基本规律。
-
在交叉学科方面,统计物理学与机器学习的结合正在开辟新的研究方向。统计物理学的原理被用来理解深度学习的工作机制,而机器学习技术也被应用于解决复杂的物理问题。
本季读书会将重点关注以上三个方向的最新进展,旨在为参与的社区成员提供一个全面而深入的学习和讨论平台。
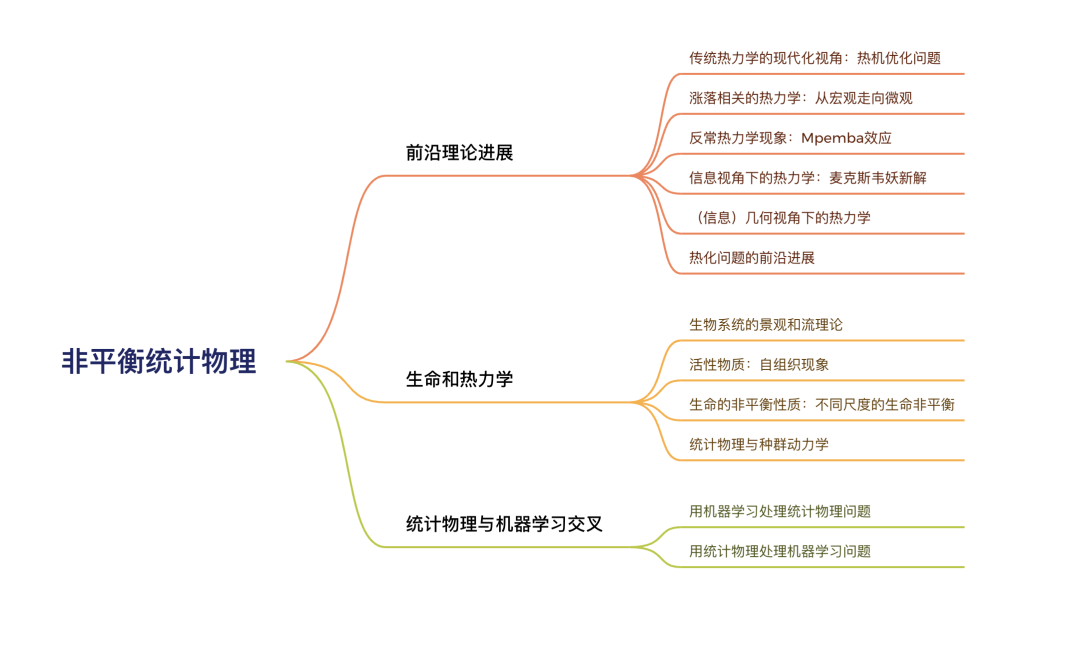
此次读书会将邀请该领域的知名学者进行专题报告。主题包括非平衡统计物理前沿理论进展、生命和热力学、统计物理与机器学习交叉三个大的方向。第一部分前沿理论涵盖热机优化问题、涨落相关的热力学、反常热力学现象、信息视角下的热力学、(信息)几何视角下的热力学、热化问题等主题;第二部分生命和热力学涵盖生命系统的景观和流理论、活性物质与自组织现象、生命的非平衡性质、统计物理与种群动力学等主题;第三部分统计物理与机器学习交叉涵盖用机器学习处理统计物理问题、用统计物理处理机器学习问题等主题。
汤雷翰,西湖大学理学院及交叉科学中心讲席教授。本科毕业于中国科技大学,1981年经李政道教授组织的CUSPEA项目赴美国Carnegie Mellon大学读研,1987年获得物理学博士学位。1996年任职英国帝国理工学院Blackett实验室讲师,1997年加入香港浸会大学物理系,历任副教授、教授。2020-2024年,他担任香港浸会大学计算和理论研究所主任。2010-2020年期间,他在北京计算科学研究中心主管复杂系统研究部。2024年受聘于西湖大学,任理学院及交叉科学中心讲席教授。
汪劲,纽约州立大学(SUNY)石溪分校化学和物理学系教授,1991年获得美国伊利诺伊大学天体物理博士。研究兴趣包括生物分子折叠的机制、分子网络的底层原理、从景观和流理论视角研究经典和量子非平衡统计物理、复杂环境中的反应动力学等。
梁师翎,德累斯顿系统生物学中心(CSBD) ELBE 博士后研究员。2024年博士毕业于瑞士洛桑联邦理工学院(EPFL)。主要研究兴趣是统计物理基础,小系统随机热力学,以及非平衡热力学在生命等复杂现象中的应用。
个人主页:https://shilingliang.com/
唐乾元,香港浸会大学物理系助理教授,集智科学家,集智-凯风研读营学者。南京大学物理学博士,曾是是日本理化学研究所博士后。研究方向:数据驱动的复杂系统研究;生物医学领域的人工智能;蛋白质进化和动力学;生物系统的复杂性和临界性。
本季读书会运营负责人
梁金,集智俱乐部公众号负责人,统计物理硕士。兴趣领域:物理,涌现,科普写作。
运行模式
从2024年12月12日开始,每周四晚 19:00-21:00,持续时间预计12周左右,按读书会框架设计,每周进行线上会议,与主讲人等社区成员当面交流,会后可以获得视频回放持续学习。
报名方式
第二步:填写信息后,付费报名。如需用支付宝支付,请在PC端进入读书会页面报名支付:https://pattern.swarma.org/study_group/54
第三步:添加运营负责人微信,获取所有推荐论文资源包,拉入对应主题的读书会社区(微信群)。
PS:为确保专业性和讨论的聚焦,本读书会谢绝脱离读书会主题和复杂科学问题本身的空泛的哲学和思辨式讨论;如果出现讨论内容不符合要求、经提醒无效者,会被移除群聊并对未参与部分退费。
加入社区后可以获得的资源:
完整权限,包括线上问答、录播回看、资料共享、社群交流、信息同步、共创任务获取积分等。

参与共创任务获取积分,共建学术社区:
读书会采用共学共研机制,成员通过内容共创获积分(字幕修改、读书会笔记、论文速递、公众号文章、集智百科、论文解读等共创任务),积分符合条件即可退费。发起人和主讲人同样遵循此机制,无额外金钱激励。

PS:具体参与方式可以加入读书会后查看对应的共创任务列表,领取任务,与运营负责人沟通详情,上述规则的最终解释权归集智俱乐部所有。
模块一:前沿理论进展
-
传统热力学的现代化视角:热机优化问题
卡诺定理告诉我们,最大效率意味着零功率输出(准静态操作)。那么,在现实世界中,我们如何在效率和功率之间找到平衡?这个主题将重新审视这个古老而现代的问题,探讨热机优化的理论极限,以及这些理论如何指导我们设计更好的能量转换系统。我们将讨论现代热力学如何重新诠释和扩展卡诺循环的概念,以及在有限时间内最大化热机效率的可能性。
[1] Curzon, F. L., & Ahlborn, B. (1975). Efficiency of a Carnot engine at maximum power output. American Journal of Physics, 43(1), 22–24. https://doi.org/10.1119/1.10023
这篇文章首次考虑现实中热机运行时间有限的情况,提出了一个重要的效率公式,开创了更贴近实际的热力学研究方向。
[2]Van den Broeck, C. (2005). Thermodynamic Efficiency at Maximum Power. Physical Review Letters, 95(19), 190602. https://doi.org/10.1103/PhysRevLett.95.190602
证明了在某些条件下(线性不可逆区间),Curzon和Ahlborn提出的效率公式具有普遍性。这一发现大大增强了我们对热机效率的理解。
[3] Esposito, M., Kawai, R., Lindenberg, K., & Van den Broeck, C. (2010). Efficiency at Maximum Power of Low-Dissipation Carnot Engines. Physical Review Letters, 105(15), 150603. https://doi.org/10.1103/PhysRevLett.105.150603
扩展了之前的研究,考虑了更广泛的热机类型,帮助我们更好地理解不同类型热机的效率极限。
[4] Tu, Z.-C. (2021). Abstract models for heat engines. Frontiers of Physics, 16, 1–12. https://doi.org/10.1007/s11467-020-1029-6
这项研究完整综述概括了各种研究热机问题的抽象模型。
[5] Rolandi, A., Abiuso, P., & Perarnau-Llobet, M. (2023). Collective Advantages in Finite-Time Thermodynamics. Physical Review Letters, 131(21), 210401. https://doi.org/10.1103/PhysRevLett.131.210401
研究了多个热机同时工作时的情况,发现它们可能比单个热机更有效率。这项研究对设计更高效的能量系统有重要启示。
-
涨落相关的热力学:从宏观走向微观
当我们把目光从宏观转向微观,热力学定律还能保持不变吗?在分子马达和纳米器件中,涨落不再是可以忽略的“噪音”,而成了主角。我们将探讨如何在这个新的尺度上重新定义热、功和效率。这个主题将深入研究涨落效应如何影响微观系统的热力学行为,以及是否存在某种适用于微观系统的“涨落热力学定律”。这些研究不仅具有理论意义,还可能为纳米技术和分子机器的设计提供重要指导。
[1] Jarzynski, C. (1997). Nonequilibrium equality for free energy differences. Physical Review Letters, 78(14), 2690–2693. https://doi.org/10.1103/PhysRevLett.78.2690
提出了一个划时代的公式(Jarsynski 等式),让我们能够通过测量非平衡过程来获得平衡态的信息。
[2] Crooks, G. E. (1998). Nonequilibrium Measurements of Free Energy Differences for Microscopically Reversible Markovian Systems. Journal of Statistical Physics, 90(5), 1481–1487. https://doi.org/10.1023/A:1023208217925
提出了一个重要公式,让我们能够从微观粒子的运动中计算出宏观的热力学量。
[3] Esposito, M., & Van den Broeck, C. (2010). Three Detailed Fluctuation Theorems. Physical Review Letters, 104(9), 090601. https://doi.org/10.1103/PhysRevLett.104.090601
总结了三个关于能量涨落的重要定理,帮助我们更全面地理解微观世界的能量变化规律。
[4] Falasco, G., & Esposito, M. (2023). Macroscopic Stochastic Thermodynamics (No. arXiv:2307.12406). arXiv. https://doi.org/10.48550/arXiv.2307.12406
将微观世界的随机热力学理论推广到了宏观尺度,帮助我们理解从细胞到整个生态系统的能量流动。这种统一的理论框架对跨尺度的系统研究非常重要。
[5] Barato, A. C., & Seifert, U. (2015). Thermodynamic Uncertainty Relation for Biomolecular Processes. Physical Review Letters, 114(15), 158101. https://doi.org/10.1103/PhysRevLett.114.158101
发现了生物分子过程中的一个普遍规律——热力学不确定原理(TUR),帮助我们理解为什么某些生物过程(如细胞内的化学反应)会有一定的不确定性。
[6] Horowitz, J. M., & Gingrich, T. R. (2020). Thermodynamic uncertainty relations constrain non-equilibrium fluctuations. Nature Physics, 16(1), 15–20. https://doi.org/10.1038/s41567-019-0702-6
一篇完整清晰的综述文章,总结了热力学不确定性原理的主要结论。
-
反常热力学现象:Mpemba 效应
在一些物理系统中,我们发现高温状态反而比低温状态更快冷却——这个看似违反直觉的现象背后隐藏着什么物理机制?它是个例还是普遍规律?这个主题将深入探讨 Mpemba 效应,挑战我们对热力学过程的固有认知。我们将讨论这种效应在其他物理系统中的普遍性,以及研究反常热力学现象如何帮助我们深化对热力学过程的理解。这个主题不仅涉及基础物理问题,还可能启发新的材料处理和工程应用。
[1] Bechhoefer, J., Kumar, A., & Chétrite, R. (2021). A fresh understanding of the Mpemba effect. Nature Reviews Physics, 3(8), 534–535. https://doi.org/10.1038/s42254-021-00349-8
这篇综述文章清晰地解释了 Mpemba 效应的最新研究进展。
[2] Ibáñez, M., Dieball, C., Lasanta, A., Godec, A., & Rica, R. A. (2024). Heating and cooling are fundamentally asymmetric and evolve along distinct pathways. Nature Physics, 20(1), 135–141. https://doi.org/10.1038/s41567-023-02269-z
这项最新研究揭示了加热和冷却过程的根本不同。
[3] Klich, I., Raz, O., Hirschberg, O., & Vucelja, M. (2019). Mpemba Index and Anomalous Relaxation. Physical Review X, 9(2), 021060. https://doi.org/10.1103/PhysRevX.9.021060
引入了“Mpemba指数”的概念,帮助我们量化和预测 Mpemba 效应。
[4] Lu, Z., & Raz, O. (2017). Nonequilibrium thermodynamics of the Markovian Mpemba effect and its inverse. Proceedings of the National Academy of Sciences, 114(20), 5083–5088. https://doi.org/10.1073/pnas.1701264114
首次为微观系统的类似于 Mpemba 效应提供了一个普适的理论框架。这项工作表明,Mpemba 效应不仅限于水,还可能在其他系统中出现。
[5] Teza, G., Yaacoby, R., & Raz, O. (2023). Relaxation Shortcuts through Boundary Coupling. Physical Review Letters, 131(1), 017101. https://doi.org/10.1103/PhysRevLett.131.017101
发现通过边界耦合加速系统冷却的方法,为 Mpemba 效应研究开辟新方向。
-
信息视角下的热力学:麦克斯韦妖新解
150年前,麦克斯韦用一个思想实验挑战了热力学第二定律。今天,我们能在实验室里实现这个“妖精”吗?这个主题将探讨信息处理与能量转换之间的深刻关系。我们将讨论近期在实验中实现类似麦克斯韦妖系统的尝试,以及这些研究对我们理解信息和能量之间关系的启示。这个主题不仅关乎基础物理,还可能彻底改变我们对计算和信息处理的理解,对未来的信息技术发展具有重要意义。
[1] Barato, A. C., & Seifert, U. (2014). Unifying Three Perspectives on Information Processing in Stochastic Thermodynamics. Physical Review Letters, 112(9), 090601. https://doi.org/10.1103/PhysRevLett.112.090601
统一了随机热力学中信息处理的三个重要视角。这项工作深化了我们对信息在物理过程中作用的理解,为进一步探索信息与能量的关系奠定了理论基础。
[2] Esposito, M., & Van den Broeck, C. (2011). Second law and Landauer principle far from equilibrium. EPL (Europhysics Letters), 95(4), 40004. https://doi.org/10.1209/0295-5075/95/40004
将兰道尔原理扩展到非平衡情况,拓展了信息擦除热力学代价的理论范围。
[3] Parrondo, J. M. R., Horowitz, J. M., & Sagawa, T. (2015). Thermodynamics of information. Nature Physics, 11(2), 131–139. https://doi.org/10.1038/nphys3230
综述信息热力学发展,清晰展示了信息在物理学中的基本地位。
[4] Sagawa, T., & Ueda, M. (2009). Minimal Energy Cost for Thermodynamic Information Processing: Measurement and Information Erasure. Physical Review Letters, 102(25), 250602. https://doi.org/10.1103/PhysRevLett.102.250602
探讨了信息处理的最小能量成本,厘清了测量和信息擦除的基本物理限制。
[5] Yan, L.-L., Bu, J.-T., Zeng, Q., Zhang, K., Cui, K.-F., Zhou, F., Su, S.-L., Chen, L., Wang, J., Chen, G., & Feng, M. (2024). Experimental Verification of Demon-Involved Fluctuation Theorems. Physical Review Letters, 133(9), 090402. https://doi.org/10.1103/PhysRevLett.133.090402
实验验证涉及 Maxwell 妖的涨落定理,将理论与实验观察结合。
[6] Zeng, Q., & Wang, J. (2021). New fluctuation theorems on Maxwell’s demon. Science Advances, 7(23), eabf1807. https://doi.org/10.1126/sciadv.abf1807
提出 Maxwell 妖的新涨落定理,拓展了信息在热力学过程中作用的理论框架。
相关文章:
-
(信息)几何视角下的热力学
这一主题将介绍如何用几何学的方法来理解热力学过程。我们将探讨热力学状态空间的几何结构,以及如何利用这种几何视角来优化热力学过程和理解相变现象。这种方法不仅提供了新的理论洞见,还可能导致新的实验设计和技术应用。
[1] Crooks, G. E. (2007). Measuring Thermodynamic Length. Physical Review Letters, 99(10), 100602. https://doi.org/10.1103/PhysRevLett.99.100602
提出了测量热力学长度的新方法,连接了宏观热力学和微观动力学。
[2] Ito, S. (2018). Stochastic Thermodynamic Interpretation of Information Geometry. Physical Review Letters, 121(3), 030605. https://doi.org/10.1103/PhysRevLett.121.030605
建立了随机热力学与信息几何之间的联系,为理解非平衡过程提供了新视角。
[3] Ito, S., & Dechant, A. (2020). Stochastic Time Evolution, Information Geometry, and the Cramér-Rao Bound. Physical Review X, 10(2), 021056. https://doi.org/10.1103/PhysRevX.10.021056
将随机时间演化与信息几何和Cramér-Rao界联系起来,深化了对非平衡动力学的理解。
[4] Li, G., Chen, J.-F., Sun, C. P., & Dong, H. (2022). Geodesic Path for the Minimal Energy Cost in Shortcuts to Isothermality. Physical Review Letters, 128(23), 230603. https://doi.org/10.1103/PhysRevLett.128.230603
发现了等温过程中最小能量消耗的测地线路径,为优化热力学过程提供了理论基础。
[5] Salamon, P., & Berry, R. S. (1983). Thermodynamic Length and Dissipated Availability. Physical Review Letters, 51(13), 1127–1130. https://doi.org/10.1103/PhysRevLett.51.1127
引入热力学长度概念,为量化热力学过程的不可逆性提供了几何描述。
-
热化问题的前沿进展
热化问题是统计物理学中的一个基本问题,涉及系统如何达到热平衡。这个主题将介绍热化问题研究的最新进展,包括量子系统的热化、非平衡态的长时间演化等。我们还将讨论这些研究对理解自然界中复杂系统行为的意义。
[1] Wang, Z., Fu, W., Zhang, Y., & Zhao, H. (2024). Thermalization of Two- and Three-Dimensional Classical Lattices. Physical Review Letters, 132(21), 217102. https://doi.org/10.1103/PhysRevLett.132.217102
[2] Liu, Y., & He, D. (2024). Chaotic route to classical thermalization: A real-space analysis. Physical Review E, 109(6), 064115. https://doi.org/10.1103/PhysRevE.109.064115
模块二:生命和热力学
-
生命系统的景观和流理论
一般的动力系统通常与环境有能量、物质和信息交换,我们需要研究非平衡动力学以理解其底层原理和机制。非平衡生物系统的景观和流理论指出,系统的动力学由景观和流共同决定:景观趋向于让系统稳定在具有较高概率或较低势能的状态或吸引盆地,流通常具有旋转特性,提供来自状态净流入或流出的额外力。平衡景观、非平衡景观和流理论在生物学领域的应用涵盖蛋白质折叠,生物分子识别,生物分子演化和平衡系统设计,细胞周期与分化,癌症,神经网络和脑功能,非平衡系统的演化,基因组结构动力学的跨尺度研究等。
[1] Wang, Jin. Perspectives on the landscape and flux theory for describing emergent behaviors of the biological systems. Journal of Biological Physics 48.1 (2022): 1-36.
文章对平衡生物系统的景观理论和非平衡生物系统的景观和流理论作为全局驱动力进行了综述。在该文中,行为的涌现、熵与自由能相关的热力学,以及速率和路径的动力学,都得到定量论证。文章还讨论了层级化组织结构。
[2] Wang, Jin. Landscape and flux theory of non-equilibrium dynamical systems with application to biology. Advances in Physics 64.1 (2015): 1-137.
非平衡生物系统的景观和流理综述。
[3] Fang, Xiaona, et al. Nonequilibrium physics in biology. Reviews of Modern Physics 91.4 (2019): 045004.
非平衡物理学在生物学中的应用。
相关文章:
前沿综述:描述生物系统涌现行为的景观和流理论视角
-
活性物质:自组织现象
为什么成千上万的鱼儿能够整齐划一地游动?细菌群落如何形成复杂的图案?这个主题将带我们探索活性物质的奇妙世界,揭示这些远离平衡系统中涌现出的集体行为。我们将讨论如何从统计物理的角度描述和预测这些自组织现象,以及这些研究如何启发新材料的设计。活性物质研究不仅有助于我们理解自然界中的集体行为,还可能为开发新型智能材料和自组装系统提供灵感。
[1] Vrugt, M. te, & Wittkowski, R. (2024). A review of active matter reviews (No. arXiv:2405.15751). arXiv. https://doi.org/10.48550/arXiv.2405.15751
综述了活性物质研究领域的主要综述文章,为该领域的发展提供了全面视角。
[2] Cates, M. E., & Tailleur, J. (2015). Motility-Induced Phase Separation. Annual Review of Condensed Matter Physics, 6(1), 219–244. https://doi.org/10.1146/annurev-conmatphys-031214-014710
阐述了运动诱导相分离的理论,解释了活性粒子系统中的集体行为。
[3] Fruchart, M., Hanai, R., Littlewood, P. B., & Vitelli, V. (2021). Non-reciprocal phase transitions. Nature, 592(7854), Article 7854. https://doi.org/10.1038/s41586-021-03375-9
引入非互易相变的概念,拓展了对活性物质中新型相变现象的理解。
[4] Howse, J. R., Jones, R. A. L., Ryan, A. J., Gough, T., Vafabakhsh, R., & Golestanian, R. (2007). Self-Motile Colloidal Particles: From Directed Propulsion to Random Walk. Physical Review Letters, 99(4), 048102. https://doi.org/10.1103/PhysRevLett.99.048102
研究了自推进胶体粒子的运动,从微观机制解释了活性物质的宏观行为。
[5] Schaller, V., Weber, C., Semmrich, C., Frey, E., & Bausch, A. R. (2010). Polar patterns of driven filaments. Nature, 467(7311), 73–77. https://doi.org/10.1038/nature09312
实验观察到驱动丝状物质形成的极性图案,揭示了活性物质中有序结构的形成机制。
[6] Tailleur, J., & Cates, M. E. (2008). Statistical Mechanics of Interacting Run-and-Tumble Bacteria. Physical Review Letters, 100(21), 218103. https://doi.org/10.1103/PhysRevLett.100.218103
建立了描述相互作用的“run-and-tumble”细菌的统计力学模型,为理解细菌集群行为提供了理论框架。
[7] Toner, J., & Tu, Y. (1998). Flocks, herds, and schools: A quantitative theory of flocking. Physical Review E, 58(4), 4828–4858. https://doi.org/10.1103/PhysRevE.58.4828
提出了群集行为的定量理论,为理解鸟群、鱼群等大尺度集体运动奠定了基础。
-
生命的非平衡性质:不同尺度的生命非平衡(震荡,感知,优化)
生命系统为什么总是处于非平衡状态?维持这种状态需要付出怎样的能量代价?这个主题将从分子马达到生态系统,探讨生命如何在效率和稳定性之间寻找平衡。我们将研究生命系统如何通过精妙的能量转换和信息处理机制来维持其非平衡状态,以及这些机制的热力学效率。这些研究不仅有助于我们更深入地理解生命现象,还可能为设计更高效、更稳定的人工系统提供启示。
[1] Yang, X., Heinemann, M., Howard, J., Huber, G., Iyer-Biswas, S., Le Treut, G., Lynch, M., Montooth, K. L., Needleman, D. J., Pigolotti, S., Rodenfels, J., Ronceray, P., Shankar, S., Tavassoly, I., Thutupalli, S., Titov, D. V., Wang, J., & Foster, P. J. (2021). Physical bioenergetics: Energy fluxes, budgets, and constraints in cells. Proceedings of the National Academy of Sciences, 118(26), e2026786118. https://doi.org/10.1073/pnas.2026786118
全面综述了细胞中的能量流动、预算和限制,为理解生命系统的物理生物能量学提供了框架。
解读文章:《物理生物能量学:非平衡物理学、能量代谢与细胞生物学的新交叉》
[2] Beard, D. A., Babson, E., Curtis, E., & Qian, H. (2004). Thermodynamic constraints for biochemical networks. Journal of Theoretical Biology, 228(3), 327–333. https://doi.org/10.1016/j.jtbi.2004.01.008
阐明了生化网络的热力学约束,为理解细胞代谢网络的运作原理奠定了基础。
[3] Cao, Y., Wang, H., Ouyang, Q., & Tu, Y. (2015). The free-energy cost of accurate biochemical oscillations. Nature Physics, 11(9), Article 9. https://doi.org/10.1038/nphys3412
量化了精确生化振荡所需的自由能代价,揭示了生物钟等周期性行为的能量要求。
[4] Lan, G., Sartori, P., Neumann, S., Sourjik, V., & Tu, Y. (2012). The energy–speed–accuracy trade-off in sensory adaptation. Nature Physics, 8(5), 422–428. https://doi.org/10.1038/nphys2276
研究了感觉适应中能量、速度和准确性的权衡,阐明了生物信号处理的基本限制。
[5] Bialek, W., & Setayeshgar, S. (2005). Physical limits to biochemical signaling. Proceedings of the National Academy of Sciences, 102(29), 10040–10045. https://doi.org/10.1073/pnas.0504321102
探讨了生化信号传导的物理极限,为理解细胞如何在噪声环境中处理信息提供了洞见。
[6] Sartori, P., & Pigolotti, S. (2015). Thermodynamics of Error Correction. Physical Review X, 5(4), 041039. https://doi.org/10.1103/PhysRevX.5.041039
分析了错误纠正的热力学,揭示了生物系统维持高保真度信息处理的能量代价。
[7] ten Wolde, P. R., Becker, N. B., Ouldridge, T. E., & Mugler, A. (2016). Fundamental Limits to Cellular Sensing. Journal of Statistical Physics, 162(5), 1395–1424. https://doi.org/10.1007/s10955-015-1440-5
探讨了细胞感知的基本限制,阐明了细胞如何在能量消耗和信息获取之间进行权衡。
相关文章:
热力学如何解释进化论:最大化熵产生原理驱动下的自然选择丨新春特辑
-
统计物理与种群动力学
在竞争激烈的自然界,为什么不同物种能够长期共存?生态系统的稳定性来自哪里?这个主题将用统计物理的视角审视这些生态学问题。我们将探讨环境波动如何影响物种多样性,以及这些研究对生态保护的启示。通过将统计物理方法应用于生态系统研究,我们可能找到预测和维护生态系统稳定性的新方法,这对于应对气候变化和保护生物多样性具有重要意义。
[1] Cui, W., Marsland, R., & Mehta, P. (2020). Effect of Resource Dynamics on Species Packing in Diverse Ecosystems. Physical Review Letters, 125(4), 048101. https://doi.org/10.1103/PhysRevLett.125.048101
[2] Cui, W., Marsland, R., & Mehta, P. (2024). Les Houches Lectures on Community Ecology: From Niche Theory to Statistical Mechanics. ArXiv, arXiv:2403.05497v1.
[3] Goldford, J. E., Lu, N., Bajić, D., Estrela, S., Tikhonov, M., Sanchez-Gorostiaga, A., Segrè, D., Mehta, P., & Sanchez, A. (2018). Emergent simplicity in microbial community assembly. Science, 361(6401), 469–474. https://doi.org/10.1126/science.aat1168
[4] Hatton, I. A., Mazzarisi, O., Altieri, A., & Smerlak, M. (2024). Diversity begets stability: Sublinear growth and competitive coexistence across ecosystems. Science, 383(6688), eadg8488. https://doi.org/10.1126/science.adg8488
[5] Melbinger, A., Cremer, J., & Frey, E. (2010). Evolutionary Game Theory in Growing Populations. Physical Review Letters, 105(17), 178101. https://doi.org/10.1103/PhysRevLett.105.178101
模块三:统计物理与机器学习的交叉
-
用机器学习处理统计物理问题
机器学习正在改变统计物理研究。从相变预测到量子多体系统模拟,机器学习算法展现出强大的潜力。这个主题将探讨如何利用深度学习、强化学习等技术来解决传统统计物理中的难题。我们将讨论这些方法的优势和局限性,以及它们如何改变我们研究复杂物理系统的方式。这个领域不仅推动了物理学研究的前沿,还为机器学习算法在科学计算中的应用提供了宝贵的见解。
[1] Martin, J., Lequerica Mateos, M., Onuchic, J. N., Coluzza, I., & Morcos, F. (2024). Machine Learning in Biological Physics: From Biomolecular Prediction to Design. Proceedings of the National Academy of Sciences, 121(27), e2311807121.
综述了机器学习在生物物理学中的应用,从生物分子预测到设计,展示了AI技术在跨学科研究中的巨大潜力。
[2] Tang, Y., Weng, J., & Zhang, P. (2023). Neural-Network Solutions to Stochastic Reaction Networks. Nature Machine Intelligence, 5(4), 376–385.
提出了使用神经网络解决随机反应网络问题的新方法,为研究复杂化学和生物系统提供了高效工具。
[3] Tang, Y., Liu, J., Zhang, J., & Zhang, P. (2024). Learning Nonequilibrium Statistical Mechanics and Dynamical Phase Transitions. Nature Communications, 15(1), 1117.
展示了机器学习如何帮助我们理解非平衡统计力学和动力学相变,为研究复杂系统的动态行为提供了新工具。
[4] Carleo, G., Cirac, I., Cranmer, K., Daudet, L., Schuld, M., Tishby, N., Vogt-Maranto, L., & Zdeborová, L. (2019). Machine Learning and the Physical Sciences. Reviews of Modern Physics, 91(4), 045002.
全面综述了机器学习在物理科学中的应用,涵盖了从粒子物理到天体物理的广泛领域,为跨学科研究提供了宝贵的参考。
[5] Carleo, G., & Troyer, M. (2017). Solving the Quantum Many-Body Problem with Artificial Neural Networks. Science, 355(6325), 602–606.
首次将神经网络应用于求解量子多体问题,开创了“量子机器学习”这一新兴领域,为研究复杂量子系统提供了新的计算范式。
-
用统计物理处理机器学习问题
统计物理学为理解和改进机器学习算法提供了独特的视角。从神经网络的能量景观到深度学习中的相变现象,物理学概念正在帮助我们揭示机器学习的内在机制。这个主题将探讨如何将统计物理的工具和概念应用于机器学习理论,包括平均场理论、自旋玻璃模型等在深度学习分析中的应用。我们还将讨论这些研究如何指导更好的神经网络设计和训练策略。这一领域的进展不仅深化了我们对机器学习的理论理解,还为发展更高效、更可靠的人工智能算法提供了新的思路。
[1] Levine, H., & Tu, Y. (2024). Machine Learning Meets Physics: A Two-Way Street. Proceedings of the National Academy of Sciences, 121(27), e2403580121.
这篇综述全面概述了物理学与机器学习的交叉研究,为理解两个领域如何相互借鉴和促进提供了清晰的路线图。
[2] Durr, S., Mroueh, Y., Tu, Y., & Wang, S. (2023). Effective Dynamics of Generative Adversarial Networks. Physical Review X, 13(4), 041004.
将统计物理方法应用于生成对抗网络(GANs),揭示了GANs训练过程中的有效动力学,为优化这一重要的生成模型提供了理论指导。
[3] Feng, Y., & Tu, Y. (2021). The Inverse Variance–Flatness Relation in Stochastic Gradient Descent Is Critical for Finding Flat Minima. Proceedings of the National Academy of Sciences, 118(9), e2015617118.
发现了随机梯度下降中方差与平坦度的反比关系,为理解深度学习中的泛化现象提供了新的物理学解释。
[4] Zdeborová, L., & Krzakala, F. (2016). Statistical Physics of Inference: Thresholds and Algorithms. Advances in Physics, 65(5), 453-552.
全面综述了统计物理学在推断问题中的应用,特别是在理解算法相变和计算复杂性方面的贡献,为机器学习中的推断任务提供了理论基础。
[5] Mézard, M., & Montanari, A. (2009). Information, Physics, and Computation. Oxford University Press.
这本经典著作系统阐述了信息理论、统计物理和计算复杂性之间的联系,为理解机器学习中的基本问题提供了坚实的理论框架。
[6] Understanding Deep-Learning as a physicist: what would Einstein do?
https://online.kitp.ucsb.edu/online/deeplearning23/tu/
点击“阅读原文”,报名读书会