本文是香港浸会大学助理教授、集智科学家唐乾元对2024年诺贝尔物理学奖的深入解读,旨在介绍物理学原理在神经网络发展中起到的关键作用,探讨物理学与人工智能这两个领域之间的深刻联系:一方面,物理学方法为理解深度学习提供了理论基础,另一方面,人工智能也正在革新传统科学研究方法。Science of AI 与 AI for Science 的这种双向互动正在加速跨学科融合,开创科学研究的新范式。
研究领域:人工智能,深度学习,统计物理,能量景观,Science for AI,连接主义
唐乾元(香港浸会大学物理系) | 作者
中国科学杂志社 | 来源
2024年10月8日,瑞典皇家科学院宣布将该年度的诺贝尔物理学奖授予John Hopfield 和 Geoffrey Hinton,以表彰他们在人工神经网络和机器学习领域的开创性贡献。这一决定在科学界内部引起了广泛热议与好奇。来自计算机科学、物理学以及相关领域的研究人员纷纷对此表示疑惑:为何传统上被视为人工智能与神经网络领域内的研究者能够获得物理学领域的最高荣誉?
实际上,John Hopfield和Geoffrey Hinton的工作恰恰展示了物理学、机器学习及神经计算原理之间的深刻联系。这些开创性的工作在统计物理学、计算神经科学与人工智能之间建立了关键桥梁,不仅对计算机科学领域意义重大,也体现了物理学在人工智能发展中的关键作用,故而能够得到诺贝尔奖委员会的认可。本文旨在介绍物理学原理在神经网络发展中起到的关键作用,探讨物理学与人工智能这两个领域之间的深刻联系,重点阐述Hopfield和Hinton如何将统计物理中的概念与模型应用于机器学习领域,建立神经计算的理论框架,为现代人工智能的发展奠定理论基础。
1. John Hopfield的贡献:
从凝聚态物理到神经计算
John J. Hopfield于1933年出生于美国芝加哥,1958年获得康奈尔大学物理学博士学位,随后在加州大学伯克利分校、普林斯顿大学和加州理工学院等知名学府任教。Hopfield早期的研究聚焦于凝聚态物理,并在激子和半导体理论方面做出了重要贡献[1,2]。这些对凝聚态系统中集体行为与涌现现象[3]的早期研究经历为Hopfield后来在理论神经科学和生物计算方面取得的突破性成果提供了关键直觉[4]。20世纪70年代,Hopfield开始探索生命科学中的物理问题,他与Jacques Ninio各自独立提出了生化反应中的动力学校正(kinetic proofreading)机制[5,6],建立了能量消耗与生物系统信息处理准确性之间的联系,为理解生物系统如何通过非平衡过程实现高特异性提供了深刻的见解,促进了非平衡热力学的发展。随后,Hopfield开始将研究的重点转向人工神经网络与计算神经科学,其最著名的成就是在1982年提出的Hopfield模型[7]。
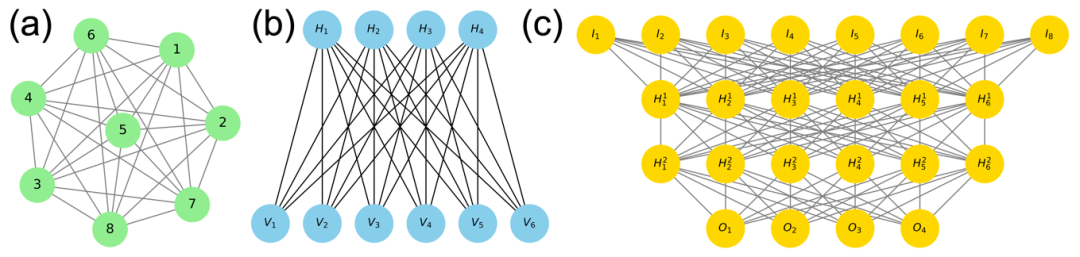
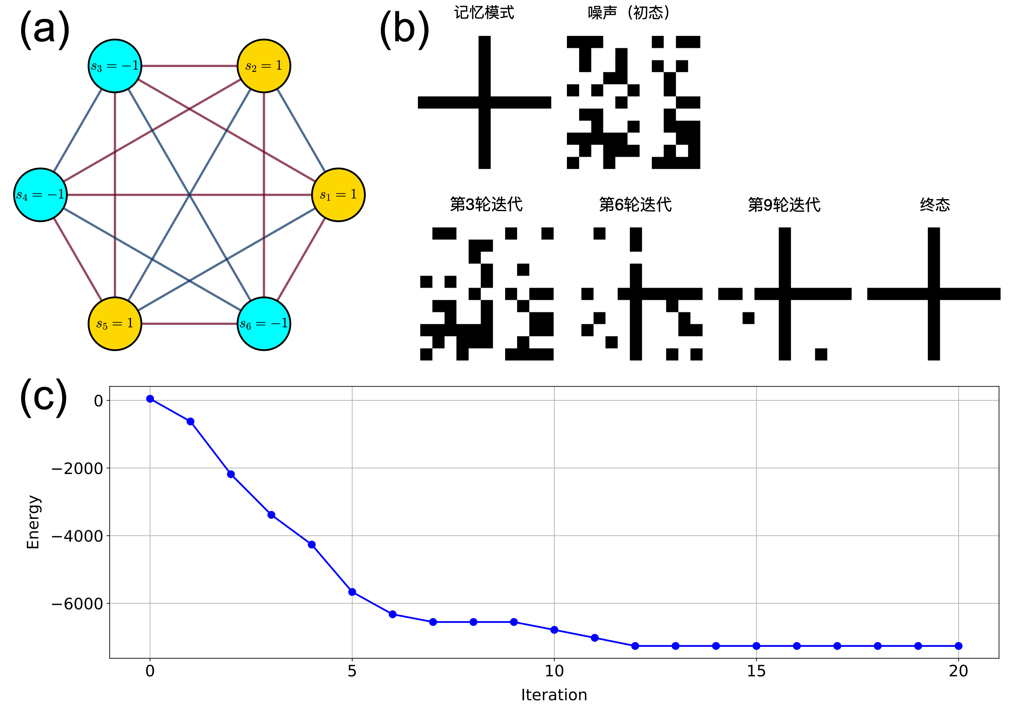
图1 Hopfield模型及其工作原理示意图。(a) 一个包含6个神经元的Hopfield网络示意图,每个圆圈代表一个神经元,其状态si可取+1或-1;连接线表示神经元间的突触连接,权重为wij。(b) 利用11×11个像素点的二值图像(每个像素值对应一个神经元状态,取值为+1或-1)展示Hopfield网络的模式存储和恢复过程。网络将“十”字形图案编码为能量最小值状态,当以随机噪声作为初始神经元状态时,经过多轮迭代更新,系统状态逐渐演化为其所记忆的模式。(c) 系统能量函数随着神经元状态的迭代更新而单调下降,最终在到达能量极小值时完全恢复出存储的图像模式
Hopfield模型[7]为机器设计了一种“联想记忆”的能力。就像人们能够通过记忆将一张模糊破损的老照片拼凑完整一样,Hopfield模型可以通过不断调整自身状态提取所记忆的信息。如图1(a)所示,Hopfield网络由N个全连接神经元组成,其中神经元i的状态用si表示,可以将其设定为±1两种状态,也可以取各种连续数值以提高网络处理模拟模式的存储和处理能力[8]。神经元之间由突触连接,神经元i与j之间的突触连接权重为wij。该网络构成了一个循环神经网络(recurrent neural network, RNN),其状态演化遵循一个简单的动力学规则, 即对于任意神经元i,其t+1时刻的状态由t时刻的状态决定:
其中,连接权重wij由Hebbian学习规则[9]确定。该规则可以简单表述成“一起激发的神经元连在一起(Neurons that fire together wire together)”:
其中,ξ代表的是网络所记忆的第μ个模式的第i分量。由上述规则描述的Hopfield网络的动力学可以描述为如下的能量函数:
该能量函数与自旋玻璃系统的能量函数在形式上完全相同[10,11]:神经元状态对应于粒子的自旋状态,突触连接对应于粒子自旋间的相互作用。如图1(b)和(c)所示,网络中存储的记忆模式对应于系统的基态,而记忆提取过程则类似于系统向局部能量极小值的弛豫过程。Hopfield模型与自旋玻璃理论都关注系统的基态与能量最小化的过程。在Hopfield模型中,通过Hebbian学习规则确定的突触权重,使得期望记忆的模式对应于能量函数的局部最小值,这些局部最小值构成了网络的吸引子。该模型为理解神经系统的信息存储与检索机制提供了重要的理论框架。
Hopfield模型证明分布式的表征可以实现稳健的信息存储,这不仅启发了生物神经系统吸引子动力学的广泛研究[12],也为后来出现的各种人工神经网络架构、类脑计算等提供了理论依据。具体来说,该模型引入了能量景观(energy landscape)作为理解神经动力学的有力工具。利用自旋玻璃中的副本方法,可以严格解析Hopfield网络的存储容量,对于随机模式,网络可以可靠地存储和检索的模式数与网络的节点数N成正比,大约为0.138N [13]。
Hopfield网络在被提出后,经历了许多拓展与创新,显著扩展了其能力和应用范围[14~16]。这些增强型架构通过高阶相互作用,或使得模型的存储容量呈指数级增长,或使得模型在噪声环境下的能力显著改善,对存储模式之间的干扰表现出更强的鲁棒性。也有学者将经典的Hopfield网络与现代的深度学习架构“注意力机制”结合起来,在模式识别任务中取得了成功[17]。这些后续工作显示了Hopfield网络并未过时,其基础原理仍在持续影响人工智能的发展。
20世纪90年代,Hopfield将注意力转向神经系统中的时间编码,尤其是嗅觉信号的处理[18]。他的工作指出,类似于物理系统中的相位锁定的同步现象也能够在生物神经网络中实现稳健的模式识别[19]。这一模型展示了时间动力学如何显著增强神经网络的计算能力,为生物系统中的信息处理提供了新的视角。
此外,值得一提的是,Hopfield还是“临界脑假说”的先驱之一。1994年,他将神经网络与Per Bak、汤超、Kurt Wiesenfeld提出的自组织临界性(即开放系统自发演化到临界状态的现象)[20]联系起来,并将其与描述地震的物理模型进行了类比[21]。1995年,Hopfield与合作者观察到了神经系统中的集体活动出现的突发性协同行为,这种协同放电活动遵循与地震系统相似的幂律分布,表明神经系统可能在临界状态附近运行[22]。这一发现为理解大脑信息处理的动力学机制提供了新的视角。
2. Geoffrey Hinton的贡献:
从统计物理到深度学习
Geoffrey Hinton于1947年出生于英国温布尔登,1970年在剑桥大学获得实验心理学学士学位,1978年获爱丁堡大学人工智能博士学位。Hinton一直活跃于人工神经网络学术研究与工业应用的第一线。自20世纪80年代以来,Hinton在人工神经网络结构设计和训练方法上做出了一系列重要贡献。他在美国卡内基梅隆大学、加拿大多伦多大学和Google公司的相关工作很大程度上推动了深度学习的诞生(或者说,深层人工神经网络的复兴)。Hinton的工作还使得深度学习在计算机视觉和自然语言处理等领域取得了突破性进展,为今天广泛应用的人工智能奠定了坚实的理论和实践基础。2019年,Hinton与另外两位深度学习领域的先驱者Yoshua Bengio和Yann LeCun一同获得了当年的图灵奖。
Hinton与Sejnowski、Ackley合作提出的Boltzmann机[23,24]是基于神经网络的概率模型的一种基础架构,体现出统计物理在机器学习中的深刻应用。在标准的Boltzmann机中,网络的所有神经元之间都允许双向连接(如图2(a)所示),其能量函数定义为
其中,wij表示连接权重,si和sj表示神经元状态(自旋),bi表示偏置项(外场)。基于该能量函数,系统状态的概率分布满足玻尔兹曼分布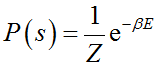 ,其中Z为配分函数,β为逆温度。其学习过程基于极大似然原理,梯度可表示为
其中,
,其中Z为配分函数,β为逆温度。其学习过程基于极大似然原理,梯度可表示为
其中, 和
和 分别表示经验分布和模型分布下的期望。Hopfield网络某种程度上可以视为确定性的Boltzmann机,而Boltzmann机可以视为随机性的Hopfield网络。然而,尽管该模型在理论上简洁优雅,但由于其全连通特性,导致训练难度较大,其广泛应用受到了限制。在该模型的基础上,后续发展出的最著名的一种模型是受限Boltzmann机(restricted Boltzmann machine, RBM)。RBM的想法最早由Paul Smolensky[25]提出,随后,Freund和Haussler[26]证明了与RBM结构一致的二值两层随机网络能够逼近任意二值向量分布,为RBM的理论发展奠定了理论基础。2000年代初期,Hinton[27]提出了高效的对比散度训练算法,并将RBM成功应用于深度学习预训练。如图2(b)所示,该架构引入了一个关键的架构约束:连接仅允许在可见层和隐藏层之间建立,消除了层内连接。这种限制显著简化了训练过程,同时保持了强大的表示能力。RBM的能量函数可以表示为
其中,v表示可见单元,h表示隐藏单元。该能量函数所对应的概率分布服从Boltzmann分布:
分别表示经验分布和模型分布下的期望。Hopfield网络某种程度上可以视为确定性的Boltzmann机,而Boltzmann机可以视为随机性的Hopfield网络。然而,尽管该模型在理论上简洁优雅,但由于其全连通特性,导致训练难度较大,其广泛应用受到了限制。在该模型的基础上,后续发展出的最著名的一种模型是受限Boltzmann机(restricted Boltzmann machine, RBM)。RBM的想法最早由Paul Smolensky[25]提出,随后,Freund和Haussler[26]证明了与RBM结构一致的二值两层随机网络能够逼近任意二值向量分布,为RBM的理论发展奠定了理论基础。2000年代初期,Hinton[27]提出了高效的对比散度训练算法,并将RBM成功应用于深度学习预训练。如图2(b)所示,该架构引入了一个关键的架构约束:连接仅允许在可见层和隐藏层之间建立,消除了层内连接。这种限制显著简化了训练过程,同时保持了强大的表示能力。RBM的能量函数可以表示为
其中,v表示可见单元,h表示隐藏单元。该能量函数所对应的概率分布服从Boltzmann分布: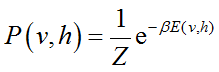 , 其中Z为配分函数。
RBM的训练最常用的是Hinton等人[27]提出的对比散度(contrastive divergence,CD)算法,其通过最小化模型平衡分布与数据分布之间的KL散度(Kullback-Leibler divergence)来实现。从统计物理的视角来看,两个概率分布之间的KL散度可以解释为数据分布 pdata(v) 与模型分布 pmodel(v) 之间自由能的差异,系统的学习过程可以表示为最小化两个分布之间的自由能差。在实践中,CD算法通过截断Gibbs采样步数来近似计算梯度,显著提高了训练效率。由于该算法在k步采样后即停止,因而该方法得名“CD-k算法”[27~29],其中的k通常取一个较小值(k=1)。这个过程类似于“受限退火”,每次进行k步采样相当于让系统进行一次短暂的退火,然后根据退火结果来调整系统参数。理论与实践都证明,虽然这种近似可能导致估计偏差,但在大多数应用场景中都能取得令人满意的效果。
深度信念网络(deep belief network, DBN)由Hinton等人[30,31]在2006年首次提出,它由多个RBM堆叠而成(如图2(c)所示)。DBN的训练采用贪婪逐层训练策略, 该训练方法显著提高了深度网络的训练效果,被认为是深度学习得以广泛应用的关键创新。实践表明,DBN在图像识别等任务中展现出良好的性能。与单层RBM相比,DBN能够学习到更加抽象的特征表示,并且在面对包含噪声的数据时仍能保持良好性能。以重整化群理论的视角来看[32],DBN方法之所以能产生上述优点,就在于其提取的特征在不同尺度上呈现了层级化的组织。
以Hopfield网络、RBM、DBN等为代表的基于能量的模型(energy-based models, EBMs)为概率密度估计和表示学习提供了一种统一的框架[33],这类模型的理论基础可以都追溯到统计物理中的自旋玻璃模型[34]。EBM通过定义能量函数来表示所希望学习的概率分布,因而也可作为生成模型(generative model)学习数据分布并生成与训练数据类似的新样本。与显式定义概率分布的模型相比,EBM具有更大的灵活性,能够建模更加复杂的依赖关系。近年来,基于能量的模型的理论仍在不断发展[35,36],同时也面临不少挑战:其中,配分函数的计算和采样效率问题仍是制约模型应用的主要瓶颈。其次,能量函数的设计缺乏系统的指导原则,往往需要依赖经验和启发式方法。此外,模型的理论性质(如表达能力、泛化性能等)亦缺乏更深入的研究。
, 其中Z为配分函数。
RBM的训练最常用的是Hinton等人[27]提出的对比散度(contrastive divergence,CD)算法,其通过最小化模型平衡分布与数据分布之间的KL散度(Kullback-Leibler divergence)来实现。从统计物理的视角来看,两个概率分布之间的KL散度可以解释为数据分布 pdata(v) 与模型分布 pmodel(v) 之间自由能的差异,系统的学习过程可以表示为最小化两个分布之间的自由能差。在实践中,CD算法通过截断Gibbs采样步数来近似计算梯度,显著提高了训练效率。由于该算法在k步采样后即停止,因而该方法得名“CD-k算法”[27~29],其中的k通常取一个较小值(k=1)。这个过程类似于“受限退火”,每次进行k步采样相当于让系统进行一次短暂的退火,然后根据退火结果来调整系统参数。理论与实践都证明,虽然这种近似可能导致估计偏差,但在大多数应用场景中都能取得令人满意的效果。
深度信念网络(deep belief network, DBN)由Hinton等人[30,31]在2006年首次提出,它由多个RBM堆叠而成(如图2(c)所示)。DBN的训练采用贪婪逐层训练策略, 该训练方法显著提高了深度网络的训练效果,被认为是深度学习得以广泛应用的关键创新。实践表明,DBN在图像识别等任务中展现出良好的性能。与单层RBM相比,DBN能够学习到更加抽象的特征表示,并且在面对包含噪声的数据时仍能保持良好性能。以重整化群理论的视角来看[32],DBN方法之所以能产生上述优点,就在于其提取的特征在不同尺度上呈现了层级化的组织。
以Hopfield网络、RBM、DBN等为代表的基于能量的模型(energy-based models, EBMs)为概率密度估计和表示学习提供了一种统一的框架[33],这类模型的理论基础可以都追溯到统计物理中的自旋玻璃模型[34]。EBM通过定义能量函数来表示所希望学习的概率分布,因而也可作为生成模型(generative model)学习数据分布并生成与训练数据类似的新样本。与显式定义概率分布的模型相比,EBM具有更大的灵活性,能够建模更加复杂的依赖关系。近年来,基于能量的模型的理论仍在不断发展[35,36],同时也面临不少挑战:其中,配分函数的计算和采样效率问题仍是制约模型应用的主要瓶颈。其次,能量函数的设计缺乏系统的指导原则,往往需要依赖经验和启发式方法。此外,模型的理论性质(如表达能力、泛化性能等)亦缺乏更深入的研究。
图2 从Boltzmann机到深度信念网络。(a) 一个包含8个神经元的全连接Boltzmann机示意图。(b) 一个受限Boltzmann机示意图,其中包含4个隐藏层节点(H1, H2, H3, H4)与6个可见层节点(V1, V2, …, V6)。(c) 一个由多层受限Boltzmann机堆叠的神经网络示意图。该网络包含4层: 一个输入层(I),两个隐藏层(H1,H2),一个输出层(O)。这4层分别包含8, 6, 6, 4个神经元。这种多层的神经网络结构不断堆叠,构成了深度信念网络
除了DBN以外,Hinton还在深度学习领域做出了其他开创性贡献,从各种理论方法的创新,再到各种创新性的模型架构和训练技术,这些工作极大推动了深度学习的理论发展和实践应用。首先,Hinton等人[37,38]关于反向传播的工作为训练深度神经网络提供了基础算法,通过对链式求导法则的巧妙应用,大大降低了模型训练的计算复杂度,使得深度网络的训练在计算上变得可行。其次,2006年,Hinton和Salakhutdinov[39]提出了使用深度自编码器(autoencoder)进行降维的方法。该工作的关键创新在于提出了一个两阶段的训练策略:(1) 对网络进行逐层预训练,即首先将输入层和第一个隐藏层构成一个RBM,使用CD算法训练这个RBM,然后用这个RBM的隐藏层激活值作为第二个RBM的输入层,逐层堆叠并训练RBM,直到完成所有编码层的预训练; (2) 使用反向传播对整个网络进行微调。实验表明,采用RBM预训练可以显著改善深度自编码器的性能,这说明无监督预训练为网络提供了一个好的参数初始化,帮助网络避免陷入不良局部极小值,从而克服了深度网络训练中的梯度消失问题[40]。
在深度学习的实践应用方面,Hinton及其合作者提出了一系列创新技术。2012年,他与学生Krizhevsky等人[41]提出的AlexNet在ImageNet竞赛中取得了优异的成绩,展示了深度卷积网络在图像识别领域的强大性能,被认为是深度学习复兴的标志性工作。同年提出的Dropout[42]是一种简单有效的防止过拟合的技术,通过在训练时随机丢弃神经元来提高模型的泛化能力。在神经网络的训练方面,Hinton提出的动量(momentum)法[43]成为深度学习训练中广泛使用的技术。2015年提出的知识蒸馏方法[44]则为模型压缩和知识迁移提供了新范式,通过使用大模型指导小模型的训练来实现知识迁移。此外,t-SNE算法[45]能够在低维空间中保持数据的局部结构特征,成为高维数据可视化的重要方法。近年来,Hinton提出了胶囊网络[46]来解决CNN在处理空间关系时的局限性;他提出的GLOM理论[47]和前向-前向网络[48]分别探索了神经表示的组织原理和新型学习范式。
纵观Hinton的研究轨迹,我们可以看到一条坚守与创新之路:他始终坚持探索基于神经网络的学习机制这一核心主题,在模型架构与优化方法等方面提出创新性解决方案。他的工作对人工智能领域产生了深远影响,使他当之无愧地被称为“深度学习之父”。
3.1 人工神经网络作为物理系统:Physics of AI
Hopfield与Hinton两位科学家的工作在物理学与人工智能之间建立起了“连接”,这种“连接”不仅体现在学科的联系上,更深刻地体现在他们对认知的理解方式——“联结主义”(Connectionism)上。联结主义是认知科学的重要理论范式,其核心主张如下:认知系统是由大量简单处理单元构成的网络[49,50];这些处理单元通过权重可调的连接相互作用,形成分布式的信息处理系统;所有认知功能,包括感知、记忆、推理等复杂的心理过程,都可以通过网络结构来实现和解释。作为联结主义的代表人物,Hopfield与Hinton的核心观点与凝聚态物理学家P. W. Anderson “More is different”的涌现论观点[51]不谋而合:复杂的认知功能是大量简单神经元通过动态连接相互作用后的涌现属性,而不能仅从单个神经元的行为来解释。深度神经网络的强大能力正是源于其具备足够的规模和复杂性,使得高层次的复杂功能能够涌现[52,53]。
统计物理与复杂系统还为理解神经网络深度学习提供了系统性工具[54]:能量景观的概念揭示了神经网络状态的演化规律[55]、自旋玻璃理论解释了神经元间的相互作用如何导致网络形成稳定的信息表征模式与学习数据的层次结构[56]。Huang和Toyoizumi[57]发展的高阶平均场理论精确描述了RBM的相态特征。Decelle等人[58]从热力学角度研究了RBM的学习动力学,发现了训练过程中的关键相变点。此外,动力系统理论为理解神经网络的非线性特性提供了关键工具[59~63]。这种动力系统视角不仅揭示了神经网络计算能力的本质,还为设计更稳健或更易于训练的网络架构提供了理论指导。在理解机器学习的工作原理方面,重整化群理论可能有助于解释深度网络的特征提取机制[64~66],动力系统理论可用于分析随机梯度下降的收敛特性和泛化行为[67~70]。此外,在扩散模型等生成模型中,随机过程理论也提供了重要的理论支撑[71,72]。此外,由于量子态的Hilbert空间具有指数级的维度,而量子叠加和纠缠等特性则为信息处理提供了独特优势[73~75],这种扩展的计算能力开辟了经典计算无法企及的量子机器学习新范式[76]。未来,随着深度学习技术的不断发展,物理学与深度学习的结合可能在许多领域重新焕发活力,推动跨学科的突破性进展。
3.2 跨学科的融合推动未来创新:AI for Sciences
Hopfield与Hinton的开创性工作展示了物理学原理在计算问题中的深远影响。通过将深度学习视为复杂动力学和涌现行为的物理系统,物理学方法为理解深度学习提供了理论基础以及与“Science of AI”相关的新研究课题。与此同时,人工智能也正在革新传统科学研究方法,形成了“AI for Science”的学术研究新范式[77]。最具代表性的是AlphaFold 2在蛋白质结构预测领域的突破性进展[78]:它将原本需要数月乃至数年的结构解析时间缩短到小时级别,极大推动了生物化学和医药研究的发展。这一成就使得其主要开发者Demis Hassabis、John M. Jumper与计算蛋白质设计专家David Baker共同获得2024年诺贝尔化学奖。此外,深度学习模型还在气象预测[79]、材料特性分析[80]和量子系统研究[81]等领域展现出强大潜力。
“Science of AI”与“AI for Science”的这种双向互动正在加速跨学科融合,开创了科学研究的新范式。这种融合不仅提高了科学研究效率,更为理解自然界提供了新的方法论,这必将不断打破传统的学科壁垒,带来影响更广泛领域的科技突破。
【致谢】 感谢国家自然科学基金(12305052)、香港研究资助局杰出青年学者计划(22302723)和香港浸会大学(RC-FNRA-IG/22-23/SCI/03)的支持。感谢集智俱乐部组织的2024年诺贝尔物理学奖专题讨论,特别感谢张江教授与尤亦庄副教授的深入见解。同时,感谢梁金与任昊达对本文初稿提出的宝贵建议。
唐乾元,香港浸会大学助理教授,集智科学家,集智-凯风研读营学者。南京大学物理学博士,曾是是日本理化学研究所博士后。研究方向:数据驱动的复杂系统研究;生物医学领域的人工智能;蛋白质进化和动力学;生物系统的复杂性和临界性。
1. Hopfield J J. Theory of the contribution of excitons to the complex dielectric constant of crystals. Phys Rev, 1958, 112: 1555-1567
2. Hopfield J J. Multiple electron-hole drop states in semiconductors. Phys Rev Lett, 1969, 23: 1422-1425
3. Anderson P W. Neural networks and physical systems with emergent collective computational properties. Science, 1988, 235(4793): 1196-1198
4. Hopfield J J. Understanding emergent computing. IEEE Comput, 2015, 48(4): 89-91
5. Hopfield J J. Kinetic proofreading: a new mechanism for reducing errors in biosynthetic processes requiring high specificity. Proc Natl Acad Sci USA, 1974, 71(10): 4135-4139
6. Ninio J. Kinetic amplification of enzyme discrimination. Biochim Biophys Acta Enzymol, 1975, 57(5): 587-595
7. Hopfield J J. Neural networks and physical systems with emergent collective computational abilities. Proc Natl Acad Sci USA, 1982, 79(8): 2554-2558.
8. Hopfield J J. Neurons with graded response have collective computational properties like those of two-state neurons. Proc Natl Acad Sci USA, 1984, 81(10): 3088-3092.
9. Hebb D O. The Organization of Behavior. New York: Wiley & Sons, 1949
10. Edwards S F, Anderson P W. Theory of spin glasses. J Phys F Metal Phys, 1975, 5(5): 965-974.
11. Hopfield J J, Tank D W. Neural computation of decisions in optimization problems. Biol Cybern, 1985, 52(3): 141-152.
12. Amit D J. Modeling Brain Function: The World of Attractor Neural Networks. Cambridge: Cambridge University Press, 1989
13. Amit D J, Gutfreund H, Sompolinsky H. Storing infinite numbers of patterns in a spin-glass model of neural networks. Phys Rev Lett, 1985, 55(14): 1530-1533.
14. Demircigil M, Heusel J, Löwe M, Upgang S, Vermet F. On a model of associative memory with huge storage capacity. J Stat Phys, 2017, 168(2): 288-299.
15. Krotov D, Hopfield J J. Dense associative memory is robust to adversarial inputs. Neural Comput, 2018, 30(12): 3151-3167.
16. Personnaz L, Guyon I, Dreyfus G. Collective computational properties of neural networks: new learning mechanisms. Phys Rev A, 1986, 34(5): 4217-4228.
17. Ramsauer H, Schäfl B, Lehner J, et al. Hopfield networks is all you need. 2021, arXiv: 2008.02217
18. Hopfield J J. Olfactory computation and object perception. Proc Natl Acad Sci USA, 1991, 88(15): 6462-6466.
19. Hopfield J J, Brody C D. What is a moment? transient synchrony as a collective mechanism for spatiotemporal integration. Proc Natl Acad Sci USA, 2001, 98(3): 1282-1287.
20. Bak P, Tang C, Wiesenfeld K. Self-organized criticality. Phys Rev A, 1988, 38(1): 364.
21. Hopfield J J. Neurons, dynamics, and computation. Phys Today, 1994, 47(2): 40-46.
22. Hopfield J J, Herz A V. Rapid local synchronization of action potentials: toward computation with coupled integrate-and-fire neurons. Proc Natl Acad Sci USA, 1995, 92(15): 6655-6662.
23. Hinton G E, Sejnowski T J. Optimal perceptual inference. In: Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, 1983. 448-453.
24. Ackley D H, Hinton G E, Sejnowski T J. A learning algorithm for Boltzmann machines. Cogn Sci, 1985, 9(1): 147-169.
25. Smolensky P. Information processing in dynamical systems: Foundations of harmony theory. In: Rumelhart D E, McClelland J L, eds. Parallel Distributed Processing: Explorations in the Microstructure of Cognition. Cambridge: MIT Press, 1986. 194-281.
26. Freund Y, Haussler D. Unsupervised learning of distributions on binary vectors using two layer networks. In: Proceedings of the 4th International Conference on Neural Information Processing Systems, 1994. 912-919
27. Hinton G E. Training products of experts by minimizing contrastive divergence. Neural Comput, 2002, 14(8): 1771-1800.
28. Carreira-Perpiñán M Á, Hinton G E. On contrastive divergence learning. In: 10th International Workshop on Artificial Intelligence and Statistics, 2005. 33-40
29. Hinton G E. A practical guide to training restricted Boltzmann machines. In: Montavon G, Orr G B, Müller K R, eds. Neural Networks: Tricks of the Trade. 2nd ed. Springer, 2012. 599-619
30. Hinton G E, Osindero S, Teh Y W. A fast learning algorithm for deep belief nets. Neural Comput, 2006, 18(7): 1527-1554.
31. Hinton G E. Learning multiple layers of representation. Trends Cogn Sci, 2007, 11(10): 428-434.
32. Mehta P, Schwab D J. An exact mapping between the variational renormalization group and deep learning. 2014, arXiv: 1410.3831
33. LeCun Y, Chopra S, Hadsell R, et al. A tutorial on energy-based learning. In: Bakir G, Hofman T, Schölkopf B, et al., eds. Predicting Structured Data. Cambridge: MIT Press, 2006. 191-246
34. Sherrington D, Kirkpatrick S. Solvable model of a spin-glass. Physical Review Letters, 1975, 35(26): 1792.
35. Du Y, Mordatch I. Implicit generation and modeling with energy based models. In: Wallach H, et al., eds. Adv Neural Inf Process Syst 32 (NeurIPS 2019). 3608-3618
36. Arbel M, Zhou L, Gretton A. Generalized energy based models. 2020, arXiv: 2003.05033
37. Rumelhart D E, Hinton G E, Williams R J. Learning representations by back-propagating errors. Nature, 1986, 323(6088): 533-536.
38. LeCun Y, Touresky D, Hinton G, et al. A theoretical framework for back-propagation. Proc 1988 Connectionist Models Summer School, 1988, 1: 21-28.
39. Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks. Science, 2006, 313(5786): 504-507.
40. Erhan D, Bengio Y, Courville A, Manzagol P A, Vincent P, Bengio S. Why does unsupervised pre-training help deep learning? J Mach Learn Res, 2010, 11: 625-660.
41. Krizhevsky A, Sutskever I, Hinton G E. ImageNet classification with deep convolutional neural networks. Adv Neural Inf Process Syst, 2012, 25: 1097-1105.
42. Hinton G E, Srivastava N, Krizhevsky A, Sutskever I, Salakhutdinov R R. Improving neural networks by preventing co-adaptation of feature detectors. Neural Comput, 2012, 24(8): 1929-1958.
43. Rumelhart D E, Hinton G E, Williams R J. Learning representations by back-propagating errors. Nature, 1986, 323(6088): 533-536.
44. Hinton G, Vinyals O, Dean J. Distilling the knowledge in a neural network. 2015, arXiv: 1503.02531
45. Van der Maaten L, Hinton G. Visualizing data using t-SNE. J Mach Learn Res, 2008, 9(11): 2579-2605.
46. Sabour S, Frosst N, Hinton G E. Dynamic routing between capsules. Adv Neural Inf Process Syst, 2017, 30: 3856-3866.
47. Hinton G E. How to represent part-whole hierarchies in a neural network. 2021, arXiv: 2102.12627
48. Hinton G E. The forward-forward algorithm: some preliminary investigations. 2022, arXiv: 2212.13345
49. Rumelhart D E, McClelland J L. Parallel Distributed Processing: Explorations in the Microstructure of Cognition. Cambridge: MIT Press, 1986
50. Smolensky P. On the proper treatment of connectionism. Behav Brain Sci, 1988, 11(1): 1-23.
51. Anderson P W. More is different. Science, 1972, 177(4047): 393-396.
52. Sejnowski T J. The Deep Learning Revolution. Cambridge: MIT Press, 2018
53. Thompson N C, Greenewald K, Lee K, et al. The computational limits of deep learning. Nat Mach Intell, 2020, 2(8): 474-483.
54. Carleo G, Cirac I, Cranmer K, et al. Machine learning and the physical sciences. Rev Mod Phys, 2019, 91(4): 045002.
55. Mehta P, Bukov M, Wang C H, et al. A high-bias, low-variance introduction to machine learning for physicists. Phys Rep, 2019, 810: 1-124.
56. Tubiana J, Monasson R. Emergence of compositional representations in restricted Boltzmann machines. Physical Review Letters, 2017, 118(13): 138301.
57. Huang H, Toyoizumi T. Advanced mean-field theory of the restricted Boltzmann machine. Physical Review E, 2015, 91(5): 050101.
58. Decelle A, Fissore G, Furtlehner C. Thermodynamics of restricted Boltzmann machines and related learning dynamics. Europhysics Letters, 2017, 119(6): 60001.
59. Jordan M I, Mitchell T M. Machine learning: trends, perspectives, and prospects. Science, 2015, 349(6245): 255-260.
60. Hochreiter S, Schmidhuber J. Long short-term memory. Neural Comput, 1997, 9(8): 1735-1780.
61. Maass W, Natschläger T, Markram H. Real-time computing without stable states: a new framework for neural computation based on perturbations. Neural Comput, 2002, 14(11): 2531-2560.
62. Lukoševičius M, Jaeger H. Reservoir computing approaches to recurrent neural network training. Comput Sci Rev, 2009, 3(3): 127-149.
63. Sussillo D, Abbott L F. Generating coherent patterns of activity from chaotic neural networks. Neuron, 2009, 63(4): 544-557.
64. Lin H W, Tegmark M, Rolnick D. Why does deep and cheap learning work so well? J Stat Phys, 2017, 168(6): 1223-1247.
65. Koch-Janusz M, Ringel Z. Mutual information, neural networks, and the renormalization group. Nat Phys, 2018, 14(6): 578-582.
66. Hou W, You Y Z. Machine learning renormalization group for statistical physics. Mach Learn Sci Technol, 2023, 4(4): 045010.
67. Wilson A C, Roelofs R, Stern M, et al. The marginal value of adaptive gradient methods in machine learning. Adv Neural Inf Process Syst, 2017, 30: 4148-4158.
68. Chaudhari P, Soatto S. Stochastic gradient descent performs variational inference. Adv Neural Inf Process Syst, 2018, 31: 6928-6939.
69. Feng Y, Tu Y. The inverse variance-flatness relation in stochastic gradient descent is critical for finding flat minima. Proc Natl Acad Sci USA, 2021, 118(9): e2015617118.
70. Yang N, Tang C, Tu Y. Stochastic gradient descent introduces an effective landscape-dependent regularization favoring flat solutions. Phys Rev Lett, 2023, 130(23): 237101.
71. Bahri Y, Kadmon J, Pennington J, et al. Statistical mechanics of deep learning. Annu Rev Condens Matter Phys, 2020, 11: 501-528.
72. Sohl-Dickstein J, Weiss E, Maheswaranathan N, Ganguli S. Deep unsupervised learning using nonequilibrium thermodynamics. In: International Conference on Machine Learning, 2015. 2256-2265
73. Cheng S, Chen J, Wang L. Information perspective to probabilistic modeling: Boltzmann machines versus born machines. Entropy, 2018, 20(8): 583.
74. Cheng S, Wang L, Xiang T, Zhang P. Tree tensor networks for generative modeling. Phys Rev B, 2019, 99(15): 155131.
75. Biamonte J, Wittek P, Pancotti N, et al. Quantum machine learning. Nature, 2017, 549(7671): 195-202.
76. LeCun Y, Bengio Y, Hinton G. Deep learning. Nature, 2015, 521(7553): 436-444.
77. Wang H, Fu T, Du Y, Gao W, Huang K, Liu Z, et al. Scientific discovery in the age of artificial intelligence. Nature, 2023, 620(7972): 47-60.
78. Jumper J, Evans R, Pritzel A, et al. Highly accurate protein structure prediction with AlphaFold. Nature, 2021, 596(7873): 583-589.
79. Lam R, Keisler R, Hinkelman L, et al. Learning skillful medium-range global weather forecasting. Science, 2023, 382(6676): 1362-1368.
80. Butler K T, Davies D W, Cartwright H, et al. Machine learning for molecular and materials science. Nature, 2018, 559(7715): 547-555.
81. Carleo G, Troyer M. Solving the quantum many-body problem with artificial neural networks. Science, 2017, 355(6325): 602-606.
2024年诺贝尔物理学奖授予人工神经网络,这是一场统计物理引发的机器学习革命。统计物理学不仅能解释热学现象,还能帮助我们理解从微观粒子到宏观宇宙的各个层级如何联系起来,复杂现象如何涌现。它通过研究大量粒子的集体行为,成功地将微观世界的随机性与宏观世界的确定性联系起来,为我们理解自然界提供了强大的工具,也为机器学习和人工智能领域的发展提供了重要推动力。
为了深入探索统计物理前沿进展,集智俱乐部联合西湖大学理学院及交叉科学中心讲席教授汤雷翰、纽约州立大学石溪分校化学和物理学系教授汪劲、德累斯顿系统生物学中心博士后研究员梁师翎、香港浸会大学物理系助理教授唐乾元,以及多位国内外知名学者共同发起「非平衡统计物理」读书会。读书会旨在探讨统计物理学的最新理论突破,统计物理在复杂系统和生命科学中的应用,以及与机器学习等前沿领域的交叉研究。读书会从12月12日开始,每周四晚20:00-22:00进行,持续时间预计12周。我们诚挚邀请各位朋友参与讨论交流,一起探索爱因斯坦眼中的普适理论!
详情请见:从热力学、生命到人工智能的统计物理之路:非平衡统计物理读书会启动!
推荐阅读
7. 加入集智,一起复杂!
点击“阅读原文”,报名读书会

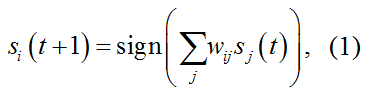

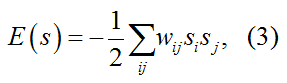
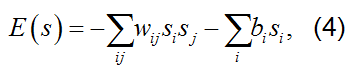
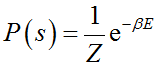 ,其中Z为配分函数,β为逆温度。其学习过程基于极大似然原理,梯度可表示为
,其中Z为配分函数,β为逆温度。其学习过程基于极大似然原理,梯度可表示为
 和
和 分别表示经验分布和模型分布下的期望。Hopfield网络某种程度上可以视为确定性的Boltzmann机,而Boltzmann机可以视为随机性的Hopfield网络。然而,尽管该模型在理论上简洁优雅,但由于其全连通特性,导致训练难度较大,其广泛应用受到了限制。在该模型的基础上,后续发展出的最著名的一种模型是受限Boltzmann机(restricted Boltzmann machine, RBM)。RBM的想法最早由Paul Smolensky[25]提出,随后,Freund和Haussler[26]证明了与RBM结构一致的二值两层随机网络能够逼近任意二值向量分布,为RBM的理论发展奠定了理论基础。2000年代初期,Hinton[27]提出了高效的对比散度训练算法,并将RBM成功应用于深度学习预训练。如图2(b)所示,该架构引入了一个关键的架构约束:连接仅允许在可见层和隐藏层之间建立,消除了层内连接。这种限制显著简化了训练过程,同时保持了强大的表示能力。RBM的能量函数可以表示为
分别表示经验分布和模型分布下的期望。Hopfield网络某种程度上可以视为确定性的Boltzmann机,而Boltzmann机可以视为随机性的Hopfield网络。然而,尽管该模型在理论上简洁优雅,但由于其全连通特性,导致训练难度较大,其广泛应用受到了限制。在该模型的基础上,后续发展出的最著名的一种模型是受限Boltzmann机(restricted Boltzmann machine, RBM)。RBM的想法最早由Paul Smolensky[25]提出,随后,Freund和Haussler[26]证明了与RBM结构一致的二值两层随机网络能够逼近任意二值向量分布,为RBM的理论发展奠定了理论基础。2000年代初期,Hinton[27]提出了高效的对比散度训练算法,并将RBM成功应用于深度学习预训练。如图2(b)所示,该架构引入了一个关键的架构约束:连接仅允许在可见层和隐藏层之间建立,消除了层内连接。这种限制显著简化了训练过程,同时保持了强大的表示能力。RBM的能量函数可以表示为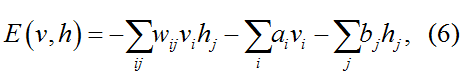
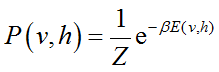 , 其中Z为配分函数。
, 其中Z为配分函数。