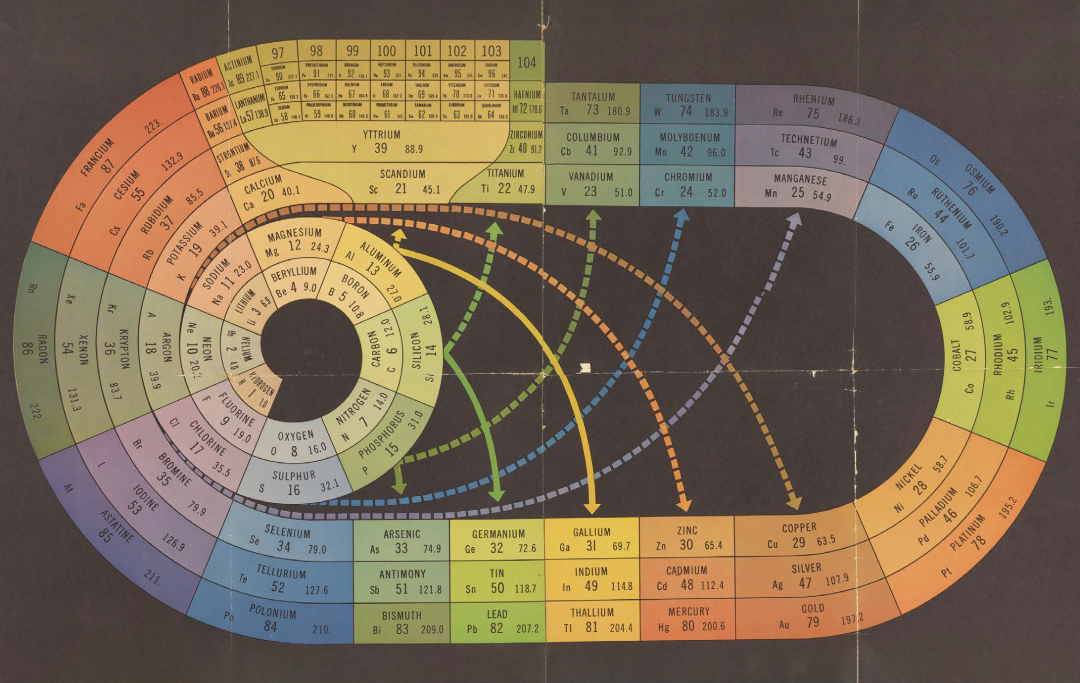
泡利不相容原理决定了化学元素间的周期性关联——无论其呈现形式如何。图片引用至 https://www.nature.com/articles/d41586-025-00731-x
物质为何稳定存在?原子为何具有特定结构?泡利不相容原理作为量子世界的基本法则,自1925年提出以来,解释了从元素周期表到恒星演化的众多物理现象。本文追溯这一原理的诞生历程、理论发展与广泛应用,展示它如何从一个“数字命理学”假设发展为解释物质秩序的关键理论,并持续指引科学家探索从原子到中子星等极端物质形态的量子本质。
研究领域:泡利不相容原理、量子力学、费米子、自旋统计定理、元素周期律、物质稳定性、量子统计、天体物理学
Olival Freire Jr、Thiago Hartz | 作者

从奇特的起源开始,泡利不相容原理已经成为一份持续馈赠科学界的珍宝。
物质何以稳定?原子为何呈现特定结构?不同材料为何在导电性、密度、熔点或光吸收谱等特性上存在差异?
自门捷列夫(Dmitri Mendeleev)于1869年提出元素周期表后的数十年间,这些问题持续困扰着物理学家。随着J·J·汤姆孙(J. J. Thomson)在世纪之交发现原子并非不可分割,而是包含带负电的亚原子粒子——电子,这些探索获得了新的动力。1911年欧内斯特·卢瑟福(Ernest Rutherford)揭示原子核的存在后,理解亚原子结构规律的科学远征正式启程。
这场发现之旅在百年之前的1925年达到了某种形式的目的地:一项自那时以来一直支撑着我们对物质稳定性理解的原理。这就是泡利不相容原理(Pauli exclusion principle),以发明它的杰出年轻奥地利理论物理学家沃尔夫冈·泡利(Wolfgang Pauli)的名字命名。
泡利于1929年在哥本哈根发表演讲。图片引用至 https://www.nature.com/articles/d41586-025-00731-x
这一诞生于”旧量子理论”时期的原理(”旧量子理论”时期是指在1900年至1925年间初探量子世界进行权宜性理论构建的时期),最终催生了维尔纳·海森堡(Werner Heisenberg)、帕斯夸尔·约旦(Pascual Jordan)、马克斯·玻恩(Max Born)、埃尔温·薛定谔(Erwin Schrödinger)、保罗·狄拉克(Paul Dirac)等人在1925-1927年间建立的自洽量子力学体系。泡利不相容原理可谓旧量子理论的巅峰之作,并罕见地跨越理论范式更迭,成功融入新量子力学体系。其百年纪念是一个契机,我们不仅追忆物理学家破解周期表预言特性、修正检验理论模型的科学远征,更应思考这一原理如何持续指引人类对物质本质的认知——不仅仅是传统意义上的物质。
对于整体上是电中性的原子而言,发现它们具有带电的亚结构,对构建原子作用机制模型构成根本性挑战。1842年,数学家塞缪尔·厄恩肖(Samuel Earnshaw)证明了静电荷分布无法形成稳定态,这直接否定了任何静态原子模型的可能性。然而,尽管在亚原子结构发现后学界进行了大量尝试,但始终未能构建出既能实现原子稳定性,又可解释元素特征(如不同元素原子发射的离散特征光谱线)的理论模型。
卢瑟福发现原子核后,丹麦物理学家尼尔斯·玻尔立即运用量子原理来解决这个问题。他运用了马克斯·普朗克在1900年为解释黑体辐射谱提出的量子化概念(即能量仅以离散形式存在),玻尔将其拓展至氢原子光谱研究。作为结构最简的原子,氢原子现已知由单个质子与单个电子构成。
玻尔初始模型设想电子绕核运行的图像,类似行星绕日轨道运动。他假设:存在特定轨道能级使电子处于非辐射态,从而保证原子稳定性。只有在两个稳定轨道之间能级差对应的频率,光才能被发射和吸收,这些轨道由首个”主量子数”[2]的不同取值表征。
这一大胆假设虽能解释氢光谱部分特征,却未达完备。玻尔继续探索,他结合了新的光谱数据和理论猜想。其理论框架部分源于经典力学,部分应用爱因斯坦1905年狭义相对论对原子电子的适用性,同时引入完全背离经典物理的量子新概念。例如,普朗克引入的“作用量量子”(现在称为普朗克常数h,其约化形式ħ=h/2π被广泛使用)表明系统能交换的能量有一个最小基元。而玻尔提出的对应原理指出,当主量子数趋大时,这种混合理论预测应渐近于经典物理结果。
这些努力促使玻尔引入了另外两个量子数[3]:角量子数(表征电子轨道角动量大小)与磁量子数(描述轨道磁矩强度)。
这些补充在玻尔的原子图像中是有意义的:电子绕核作圆周运动必然具有角动量,而带电体的轨道运动自然产生磁矩。
然而,这理论仍然不能解释氢光谱的所有特征。到了1923-24年,当时的核心难题是如何解释塞曼效应,即当绕核电子与外部磁场相互作用时会出现新的谱线。这时,泡利进入了这个故事。
在1925年的转折点上,泡利年仅24岁。作为德国汉堡大学的理论物理学讲师,他深受同行的尊敬。自维也纳青年时期起,他就被誉为数学神童——然而这一光环并未令他感到自在,这种情况并不少见。他通过心理学家卡尔·荣格(Carl Jung)推广的新精神分析寻求帮助,并与荣格保持着长期的思想对话[4]。泡利保持着极为活跃的学术通信,其公开出版的书信集对科学家和历史学家都是重要的研究素材。
泡利原理[1]虽受到埃德蒙·克林顿·斯通纳(Edmund Clifton Stoner)思想的启发,但他的方法在许多方面是原创且不同寻常的。首先,它似乎主要基于数字命理学(numerology),与已知物理学没有直接联系。泡利对玻尔模型的关键补充是引入第个四量子数——不同于玻尔的量子数,它没有经典物理的对应项,也无法在时空坐标系中具象化表征。这个被命名为自旋的新量子数仅能取两个离散值:+ħ/2或−ħ/2。具有相反自旋量子数值的电子会与外部磁场有不同的相互作用,导致在塞曼效应中观察到的谱线分裂。
如今我们知道,自旋量子数无法用视觉来解释:如果你尝试将电子建模为沿轴旋转的带电体,你会发现它的表面旋转速度会超过光速。这是原子模型中最强烈的指示之一,表明量子理论是多么奇异,充满了违背经典直觉的特点。
泡利提出不相容原理时,并没有基于经典理论或动力学原理,而是将其作为一个简单的假设提出:即在同一个原子中,没有两个电子能拥有相同的四个量子数。正如历史学家约翰·海尔布朗(John Heilbron)所评述,这原理的表述方式颇具《圣经》中十诫的风格:“禁止存在两个……具有完全一致量子数值的电子”[5]。就此而言,泡利预见了新量子力学的发展特征,这种特征令许多物理学家,包括薛定谔和爱因斯坦感到困扰——因为它在理论构建或解释中放弃了直观的视觉模型。
泡利提出不相容原理的学术背景,实则嵌套于新量子理论[3]框架下关于物质稳定性的深层论辩之中。这种理论范式转换衍生出诸多待解难题,例如,如果电子轨道是稳定的,为什么电子会在它们之间跃迁?直到1927年,当狄拉克提出了电磁场的量子理论时,才最终诠释了这种“自发衰变”是如何根据新理论运作的[6]。
到了20世纪20年代末,物理学家们逐渐认识到泡利不相容原理在物质稳定性方面起着关键作用。今天的学生会学到该原理时,会明确其适用范围为费米子的一类粒子。这些粒子具有半整数自旋,单位为ħ。这类粒子遵循由狄拉克和恩里科·费米于1926年独立提出的费米-狄拉克统计(Fermi–Dirac statistics)[7]。其他量子系统,如光子,则遵循不同的定律,即玻色-爱因斯坦统计(Bose–Einstein statistics)(该统计源于爱因斯坦与印度物理学家萨特延德拉·纳特·玻色的合作)。
寻找不相容原理、量子统计与物质稳定性之间的严格数学联系持续了几十年。自1925年泡利论文发表及费米-狄拉克统计理论建立后,学界确认了电子具有½的自旋并遵循这些统计规律,但自旋与统计间本质关联的严格证明迟至1939年方由泡利门生马库斯·菲尔斯首度完成。此后短期内涌现多篇论证,最著名的是泡利本人在1940年的一个证明[8]。1964年,雷蒙德·斯特里特(Raymond Streater)与阿瑟·怀特曼(Arthur Wightman)将此类成果正式命名为”自旋统计定理”[9]。
弗里曼·戴森(Freeman Dyson)在1967年证明了不相容原理不仅是物质稳定性的充分条件,而且是一个必要条件。他在文章[10]开头引用了保罗·埃伦费斯特(Paul Ehrenfest)在1931年说过的话:“我们取一块金属或石头。当我们思考它时,我们会非常惊讶:这些量的物质竟然占据了如此大的体积。确实,如果分子紧密地堆积在一起,每个分子中的原子也是这样紧密地堆积。那么为什么原子本身也这么大吗?答案:仅仅是因为泡利原理‘同一状态不能有两个电子’。这就是为什么原子显得如此大,如此不必要的大,以及金属和石头显得如此庞大的原因。”
戴森所属的数学物理学家新群体于20世纪60年代兴起,他们将物质稳定性作为从一般原则推导出的数学定理来研究。第一个这样的定理由戴森和安德鲁·莱纳德(Andrew Lenard)在1967年提出并证明[11],该论证被学界称为数理物理学史上最复杂的证明之一。艾略特·利布(Elliott Lieb)和沃尔特·蒂林(Walter Thirring)在1975年提供了一个更简短、更优雅的证明[12]。在这些进展的辩论中,不相容原理处于核心地位。
泡利于1945年因不相容原理获得诺贝尔物理学奖。该原理已成为我们理解元素周期表的关键支柱:通过四个量子数和不相容原理,得以构建一个按原子序数升序排列的周期律表格,并深化理解其运作机制。
不相容原理也为更奇特的物质形态提供了指导。一个例子是中子星,它是超新星爆发后留下的坍缩核心。中子星中的物质密度与原子核相当,尽管它们直径约为十公里。中子星最早是在1967年通过射电光谱学首度探测到的,但早在20世纪30年代就有人对其进行了理论预测。中子星存在的关键是“中子简并压力(neutron degeneracy pressure)”,这是泡利不相容原理的结果。随着构成恒星核心的核物质在其自身引力下压缩,电子开始与质子结合形成中子,这些中子都在争夺进入最低能态。泡利原理阻止所有中子进入最低能态,从而为星体设定了坍缩极限。类似的过程也会发生在白矮星中,这些是质量较小的太阳型恒星的坍缩残骸。
奇异型玻色-爱因斯坦凝聚体不遵循泡利不相容原。图片引用至 https://www.nature.com/articles/d41586-025-00731-x
正如自旋统计定理所表明的那样,并非所有粒子都是费米子,因此并不都遵循泡利原理。不同于费米子,在特定条件下,玻色子可以经历一种相变,在此过程中它们全部进入相同的量子态。直到20世纪末,具有这种性质的物质形式——玻色-爱因斯坦凝聚体——才在实验室中制造成功。埃里克·康奈尔(Eric Cornell)、沃尔夫冈·凯特勒(Wolfgang Ketterle)和卡尔·威曼(Carl Wieman)因此共同获得了2001年的诺贝尔物理学奖。
在过去的一个世纪中,泡利不相容原理是持续馈赠科学界的珍宝。从天体物理到凝聚态物理(该领域为晶体管及二十世纪诸多技术革命奠定物质基础),泡利不相容原理始终指引着人类对粒子行为的理解范式。曾被视作近乎玄学的数字命理,已然蜕变为现代科学的重要支柱。
-
Pauli, W. Z. Phys. 31, 765–783 (1925).
-
Bohr, N. Lond. Edinb. Dublin Phil. Mag. J. Sci. 26, 1–25
-
Duncan, A. & Janssen, M. Constructing Quantum
Mechanics Vol. 1 & 2 (OUP, 2019 & 2023).
-
Enz, C. P. No Time to Be Brief (OUP, 2010).
-
Heilbron, J. L. Hist. Stud. Phys. Sci. 13, 261–310 (1983).
-
Dirac, P. A. M. Proc. R. Soc. Lond. A 114, 243–265 (1927).
-
Monaldi, D. in The Oxford Handbook of the History of
Quantum Interpretations (ed. Friere, O.) 255–280 (OUP,
-
Pauli, W. Phys. Rev. 58, 716–722 (1940).
-
Borrelli, A. in Compendium of Quantum Physics (eds
Greenberger, D., Hentschel, K. & Weinert, F.) 733–736
-
Dyson, F. J. J. Math. Phys. 8, 1538–1545 (1967).
-
Dyson, F. J. & Lenard, A. J. Math. Phys. 8, 423–434 (1967).
-
Lieb, E. H. & Thirring, W. E. Phys. Rev. Lett. 35, 687–689
“复杂世界,简单规则”。
集智俱乐部联合复旦大学智能复杂体系实验室青年研究员朱群喜、浙江大学百人计划研究员李樵风、清华大学电子工程系数据科学与智能实验室博士后研究员丁璟韬、美国东北大学物理系Albert-László Barabási指导的博士后高婷婷、北京大学博雅博士后曹文祺、复旦大学数学科学学院应用数学方向博士研究生赵伯林、北京师范大学系统科学学院博士研究生牟牧云,共同发起「复杂系统自动建模」读书会第二季。
读书会将于9月5日起每周四晚上20:00-22:00进行,探讨四个核心模块:数据驱动的复杂系统建模、复杂网络结构推断、具有可解释性的复杂系统推断(动力学+网络结构)、应用-超材料设计和城市系统,通过重点讨论75篇经典、前沿的重要文献,从黑盒(数据驱动)到白盒(可解释性),逐步捕捉系统的“本质”规律,帮助大家更好的认识、理解、预测、控制、设计复杂系统,为相关领域的研究和应用提供洞见。欢迎感兴趣的朋友报名参与!
复杂系统自动建模读书会:从数据驱动到可解释性,探索系统内在规律|内附75篇领域必读文献
6. 加入集智,一起复杂!














