什么是对系统建模？

地图是一个可以将我们的世界模型化的工具，虽然地图远远不能代表世界本身，但地图的存在可以帮助我们快速理解世界的特征和本质。可以看出，对系统模型化——也就是对系统建模，就是对系统本身的抽象过程，我们通过建模的方法来理解系统。

将复杂的、难以理解的系统抽象为一个可理解的模型，这样的想法是一个创举。以地图为例，中国的地图最早见于2400年前的战国——这说明我们很早就已经使用建模的思路来指导实践活动。地图的核心思路是：将现实世界按比例缩小后再进行描述。现在，这种模型十分普遍，商店出售的飞机模型、地球仪等等都是等比缩小的结果。

早期的中国地图

然而使用“等比缩小”方法建立的模型，对于绝大多数系统来说，都只能描述系统的外观，而远远不足以描述系统是如何运作的。

近期，集智俱乐部发表了多篇科普文章来说明为什么“等比缩放”的模型不能描述系统的运作原理，这便是规模法则。简而言之，这是因为当对系统进行等比缩放时，系统的各个变量和指标并不会随着系统规模的变化进行相同的缩放，而通常与系统规模成幂律关系。

详情请见

从大西部号的疯狂远征谈起——规模、可控与复杂

小小的披萨问题蕴含着大大法则

论怪兽哥斯拉的规模法则

克莱伯定律揭秘生命第四维

那么，我们又该怎样现实地、可靠地将模型上的观察所得应用于真实大小的系统中呢？这是建模理论关注的重要问题，举个例子，制作一个轮船模型来展示轮船的外观非常容易，但我们应该如何制作一个轮船模型来测算轮船在海上航行时遇到的阻力大小呢？这个问题看起来非常复杂。

而建模理论的难点和重要意义也就在于此：如果这个问题可以被克服，那就意味着我们可以在模型上进行各种试验，因为模型能够反映实际系统的运作机理，所以这些实验效果将会和真实系统的效果相同——这就大大降低了试错成本，会极大的推动工业行业的发展。

大东方号（SS Great Eastern）

与建模的起源

在不久前，我们曾经聊到过大东方号的例子，详见从大西部号的疯狂远征谈起——规模、可控与复杂：大东方号轮船的设计制造是十九世纪一次跨越式的、疯狂的工业尝试。天才工程师依桑巴德试图制造一艘世界上最大轮船，这艘轮船的长度是当时世界上最长轮船的两倍，而排水量是其十倍。但不幸的是，制成后的大东方号并没有按照人们的预期表现非凡——相反地，它频繁的遭遇故障，实际运行效率也远远低于预期，最终被拆解。

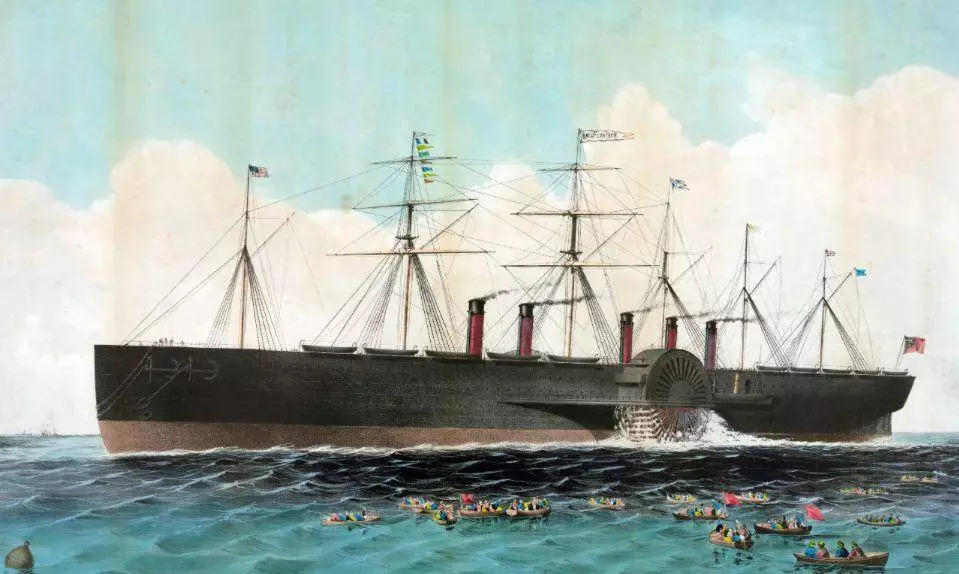
大东方号

我们可以将一次工业实践的失败进行多方面归因，现在，让我们更深入一些，尝试以更“基础科学和系统建模理论”的角度来更深入的说明它失败的原因。相信这些分析会帮助你更深刻的认识系统建模的本质。

实际上，在大东方号时代，造船业并不存在什么“真”科学，设计与制造船只的成功来自于反复尝试所积累的经验和技巧——大东方号的主设计师依桑巴德找到曾经求学于牛津大学的数学天才、造船工程师威廉·弗劳德 William Froude(1810-1879)。要求弗劳德研究能够最大限度地减小水流粘性阻力的最优船型是什么样的。

威廉·弗劳德 William Froude(1810～1879)

弗劳德的研究成果为整个航运业带来了巨大的影响，更为重要的是，弗劳德天才地引入了“系统建模（modeling a system）”的革命性概念——通过对轮船系统进行建模来研究轮船的真实运行情况。这是人类第一次尝试使用对系统建模的方法来指导工业生产，现代轮船设计科学也就此诞生。

一般来说，我们解决此类问题的关键在于将问题数学化。实际上，通过精确的方程来完全描述轮船的运行过程难度极大。这是因为水与自身存在着复杂的相互作用和反馈机制，这些复杂的机制使得描述水运动的方程——维纳-斯托克斯方程（Navier-Stokes equations）——是非线性的，这就如同蝴蝶效应一般，一点小的扰动会给其他部分带来指数级影响的提升，这就使得方程不可解。

正是意识到了这个问题的难度，弗劳德开始转变思路，他发明了新的方法论，从而试图确定小尺寸的轮船模型中得到的量化结论该如何应用于实际大小的轮船中。他做出的深远贡献在于：提出了一个定量的数学策略，找到了从小尺寸模型到实际大小物体的缩放方法。

跨越系统规模的永恒存在

——无量纲数

弗劳德巧妙的意识到，决定小尺寸模型与实际大小的船只运动特征的关系取决于一个特定的常数，他不随系统规模的改变而改变，后来人们将这个常数称为“弗劳德数（Froude number）”。

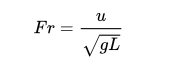
弗劳德数（Froude number）

让我们来对弗劳德数的运算稍作解释：Fr代表弗劳德数，等式右边的u代表流体速度，L代表物体的特征长度，g代表重力加速度。无论轮船的尺寸、形状、或者构成成分如何，弗劳德数只与船的行驶速度和船身长度有关。

事实上，这一比例在所有涉及运动的物理过程中都扮演着核心角色，无论是加速的子弹还是奔跑的恐龙，无论是天上的飞机还是海里的轮船。

一个怀表齿轮系统建模

弗劳德意识到的关键点在于，由于弗劳德数值相同，不同尺寸，不同运行速度的物体表现的方式仍然相同。由此一来，只要让模型船的长度和速度与实际船只的长度和速度拥有相同的弗劳德数值，就能够在建造之前确定轮船的动力学行为了。

弗劳德的行为影响深远，以至于这一规律也被应用于风洞，对莱特兄弟产生了极大影响。而这个例子为后续的建模理论提供了一套样板：即找寻规模缩放下的不变规律来搭建模型与实际系统之间的桥梁，从而理解和描述实际系统的运作机理。那么，这个所谓的不变规律到底是什么？实际上，在大多数时候，这种不变规律的代表，都是可以量化系统运作原理的无量纲数。

让我来举例说明这是什么意思：人们在日常生活中遇到的数通常伴随着衡量他们的单位，例如，披萨的直径是10厘米，披萨的周长是31.4厘米。然而，决定着周长和直径的关系的数字π却没有单位的纯数字，π就是一个典型的无量纲数。如果仔细观察公式，你就会发现弗劳德数也是一个无量纲数。

披萨与π

类似π的无量纲数的适用范围极其普遍：无论一块披萨的周长与直径的比值，还是银河系的周长与直径的比值都是同样的数字。因此，这些无量纲数在一切物理系统中扮演着重要的角色，它们定量的描述了系统性质，也量化了我们生活的这个世界的物理规律，所以寻找这些无量纲数不但成为了建模理论的核心问题之一，而且成为了物理学中的重要话题。

计算时代的系统建模

——建模的未来

得益于今天计算机算力的发展，人们开始有能力对原来不可解的方程进行“暴力求解”。在前面我们曾说，正是由于水的运动所遵循的方程是非线性的不可解方程，才让弗劳德转变思路去进行系统建模的探索。而今天人们则有了更强的计算能力，以至于我们有能力直面复杂的非线性方程——我们会通过计算机来求出非线性方程的近似解。

有趣的是，这正是今天所有的汽车、客机的外观都越来越趋同的原因，因为大家都在试图减小空气阻力，也就是说，大家都在试图优化同一组方程。而在几十年前，汽车则有着远比今天更多样化的设计。

1957年的斯蒂庞克鹰与今天的特斯拉Roadster

而有了计算机的加持，系统建模也不再局限于物理系统，科学家们开始对生物系统、社会系统和经济系统进行建模，从中观察到非常有趣的社会性质，也不乏大量的商业应用。

集智俱乐部曾经报道过科学家们关于果蝇大脑神经网络连接的近乎完全建模，从而试图了解果蝇的思维机制，详见《科学家成功绘制出完整的果蝇大脑神经网》，我们也曾报道过过关于社会系统建模的精彩例子，科学家们通过多主体模拟的方式建模社会系统，从而模拟出灾难降临时的最优疏散方案，详见《《复杂》作者science综述：与时俱进的多主体仿真模型》。

此外，我们也曾谈过使用多主体模拟的方式对公司进行建模，从而大幅图提升公司效率，具有极大的商业价值，详见“AI&Society系列多主体模拟”相关文章。

不难发现，今天计算机的发展大大提升了人类的建模能力，使我们更加靠近建模的核心：建模即是对系统的本质机理的抽象，它能赋予我们理解系统的能力，更能允许我们进行大量实验，帮助我们在现实生活中——无论是工业生产中，还是科学研究中找到最优答案。