作者：杰弗里·韦斯特

杰弗里·韦斯特，现年78岁，著名理论物理学家。全球复杂性科学研究中心、——圣塔菲研究所前所长，入选《时代周刊》全球最具影响力100人。数十年致力于“规模”（Scale）的研究工作，其研究成果被应用在理解生命体、城市可持续发展、企业运营等众多领域，被业内奉为“跨学科诺贝奖”的不二人。 

生命体、城市、公司，乃至一切复杂万物，是否都存在相通的内在生长逻辑？制约生命与死亡、城市化的扩张及公司寿命的决定因素究竟是什么？人类能否通过融汇生物学、物理学、社会学、经济学等跨学科知识，找到揭开复杂万物生长背后的简单法则？在韦斯特眼中，规模成为衡量世间万物的不变标准，利用规模法则，复杂世界变得可量化、可预测、清晰明了且极度统一。

《规模》将帮助你重新思考生命、认识自身、了解你的生活与工作，并告诉你复杂世界其实充满简单的逻辑，只要跳脱思维框架，打破学科限制，你就会重新看清你周遭的一切。

张江作为韦斯特的科研合作伙伴和《规模》中文版的校译者，将在集智AI学园网站，为《规模》读者和复杂性科学爱好者开设一场线上讲座，从规模法则、新陈代谢与生长和网络模型等方面，对《规模》一书和韦斯特的研究做深入解读。

讲座时间：7月5日（本周四）19:00-20:30

扫描下方二维码或点击阅读原文即可进入直播间：

直播地址，提前收藏

假设某天你走进比萨店，点了一个直径为9英寸[①]的比萨并付了钱。经过几分钟的等待，店员突然走过来跟你说：“抱歉，我们的9英寸比萨已经卖完了，我给您换成两个 5 英寸的吧？”那么，你该不该接受店员的建议呢？

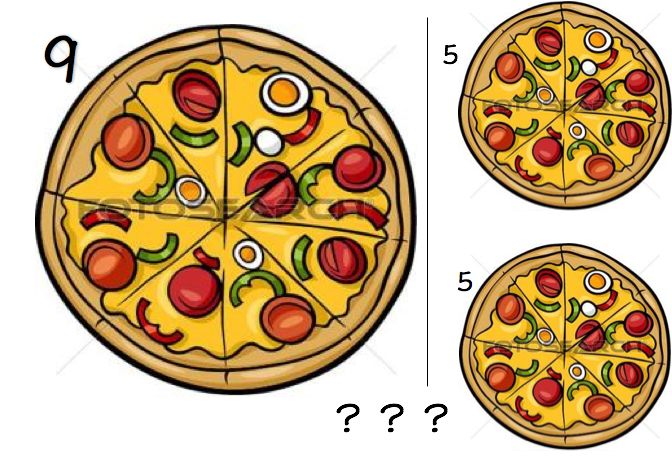
9英寸和两个5英寸

这个问题看似很简单，两个 5 英寸的比萨加起来应该是一个 10 英寸的比萨，比一个 9 英寸的还大，你可以占点儿小便宜，但其实这个建议对你是非常不划算的。因为两个直径为5 英寸的比萨的总面积要远小于一个直径为 9 英寸的比萨的面积！为什么会这样呢？

答案就在于圆的面积公式为 S =πr2。当圆的直径变成了原来的一半的时候，面积减少为原来的 1/4，而不是一半。因此，两个 5 英寸比萨的面积会是一个 9 英寸比萨的 2/3 还不到，如果你接受店员的建议，就吃了一个大亏。

这是一个隐藏在我们日常生活中的非线性规模法则的典型案例。所谓规模法则，就是指事物的某变量会与事物的规模呈现清晰的，通常是非线性的幂律关系。在这个例子中，我们用比萨的直径来衡量它的规模，这样面积就会与规模呈现平方的幂律关系，但是，我们可怜的大脑早已习惯了按线性的方式进行外推，从而掉入了这个非常隐蔽的陷阱。

事实上，这种线性思维错误是非常容易发生的，即使训练有素的科学家也不例外。例如，在《规模》一书中，作者就提到了一组科学家因没有认识到非线性规模法则而导致一头名为图什科的大象意外死亡的惨痛案例。事情是这样的：为了测试 LSD 这种致幻剂对大象的作用，科学家根据 LSD 在猫身上的正常剂量进行了简单的线性外推，结果酿成了悲剧。他们以为，因为大象的体重大约是猫的600 倍，所以，如果猫的 LSD 适用剂量是 0.5 毫克，那么就应该给大象注射 300毫克的 LSD。结果，在 300 毫克 LSD 注射完之后的 5 分钟内，大象图什科开始大叫起来，轰然倒下，重重地摔向右侧，排便，并进入持续癫痫状态，然后在 1 小时 40分钟后就死了。这是一次没有认识到非线性规模法则的惨痛教训。

要想计算大象的适用剂量，我们需要认识到克莱伯定律，它指出生物体的代谢率会随生物体规模（体重）遵守指数为 3/4 的规模法则。这意味着，当生物体的体重变为原来的 600 倍时，它的代谢率却没有提高到原来的 600 倍，而是原来的约 121倍。生物体对 LSD 的消化与其代谢能力相关，因此大象能够承受的剂量也是猫的约 121倍，这要远远小于科学家对大象注射的剂量。

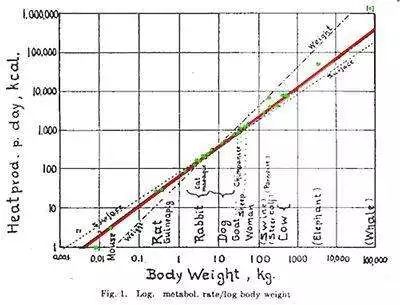
克莱伯定律

这种规模法则不仅适用于生命体，而且同样适用于城市和公司。《规模》一书中指出，随着城市人口的增长，城市的基础设施，如加油站数量、公路长度、总耗电量等并不会等速增长，而是比人口的增长速度更慢，这体现了城市的规模报酬递减效应，也就是城市越大，基础设施的使用效率会越高。更令人着迷的是，随着城市规模（人口）的增长，人与人之间的交互和合作效应就会越来越明显，因此也会创造越来越多的财富。例如，洛杉矶的人口差不多是费城的两倍，但是洛杉矶所创造的财富比费城的两倍还多，差不多是 2.2 倍。这解释了为什么大城市会比小城市更具吸引力，因为随着城市规模的增长，人均财富也会随之增长。

同样的规模法则也制约着大大小小的公司。我与圣塔菲研究所的克里斯·肯佩斯（Chris Kempes）及作者韦斯特的合作研究结果表明，新公司与老公司有着完全不一样的规模法则。对新创公司来说，它们的销售业绩会随着公司的员工数的增长呈超线性增长，这意味着企业每多雇一名员工就会获得更高的人均销售业绩。

所以，新创公司充满了创造超预期利润的可能性，因此相对于那些呈线性增长的公司显得更有活力。对一些老公司来说，每增加一名员工就可能会得到相等或更低的人均销售业绩，这恰恰反映了每个大企业都害怕的“大企业病”。同时，它也解释了为什么像阿里巴巴、腾讯这样的大公司都会在内部引入竞争机制，并鼓励内部创业。这些公司希望模仿初创企业，让员工通过类似集市一样的自组织形成一个个小团队，从而获得超线性增长。

我与香港城市大学的吴令飞的合作研究还表明，即使是虚拟网络社区也展现出了类似的规模法则[②]。对那些自组织特征明显、表现非常活跃的网络社区或论坛来说，随着用户人数的增长，平均每个用户会创造更多的内容和活动；对那些不活跃、自组织特征不显著的社区来说，人均发帖量反而会随着社区的规模（用户人数）的增长而减少。我们甚至可以用规模缩放的幂指数来衡量在线社区的黏性程度。这种黏性度量会消除时间因素和规模因素，可以刻画在线社区的内在属性[③]。          

无论我们用什么指标来度量，如长度、身高、体重、人口数、员工数等，任何复杂系统都有其特定的规模尺度，并起到极其重要的作用，因为几乎所有的其他变量，包括生物体的代谢率、寿命、心率，城市的专利数量、犯罪率、基础设施数量，公司的资产、收益、成本、盈利等都与其规模形成了规模法则。

《规模》不仅系统性地探索了这些普遍存在于各类复杂系统中的规模法则，还将它与其他已知的科学事实和规律相结合，为生物体、城市和公司构造了一个定量化的理论框架。在这一框架下，《规模》推导出了大量有意思的、令人吃惊的科学结论。

为什么所有的哺乳类动物一生的心跳次数都是 15 亿次左右？为什么人类会衰老和死亡？衰老过程有哪些重要影响因素？为什么所有生物体在成长到一定阶段就停止了生长？为什么城市的扩张却似乎从未停止过？城市作为超级生物体是如何摆脱死亡的厄运的？为什么大量的公司都活不过 10 年？所有这些都是重要的理论问题。

在没有医生指导的情况下，我们应该如何确定婴幼儿的服药剂量？我们怎么做才可以减缓自身的衰老过程？为什么我们的生活节奏变得越来越快？为什么即使大城市存在污染、犯罪、交通堵塞等问题，人们还在不断涌入大城市？这些是每个人都关心的问题。

为什么哥斯拉这种怪兽在现实中根本就不可能存在？为什么超人的神秘力量是不符合基本科学原理的？这些问题关系到“幻想文学”。当然还包括可持续发展、科技创新及奇点临近等关系到国计民生，甚至整个人类的大问题。

《规模》真可以说是包罗万象、气吞山河。我们不得不佩服作者韦斯特的气度和深厚功底。难怪比尔·米勒（Bill Miller）评论道，如果存在一个跨学科诺贝尔奖的话，那么韦斯特就是最合适的候选人。

在众多结论中，最有意思的一部分是规模法则会导致不同的生长现象。

为什么所有的生物体在成年以后就停留在一个固定的尺寸而不再生长了呢？将规模缩放理论和生物体的能量预算方程结合起来，我们就能推导出所有生物体都适用的生长方程，该方程不仅能够严丝合缝地拟合很多生物体的成长曲线——也就是给出体重随年龄变化的精确定量关系，而且能够回答为什么所有生物体的生长会存在一个体重上的极限，它们长到一定程度就停止生长了。

问题的答案就在于生长速度的不匹配。如果我们将生物体理解为一个大水缸，那么它代谢摄入的能量就是流进水缸里面的水，它为了维护、修复自身而消耗的能量就是流出的水，而它的体重就是水缸中的水。很显然，生物体的成长就相当于水缸中水量的增长，它取决于净流入量，也就是流入–流出。

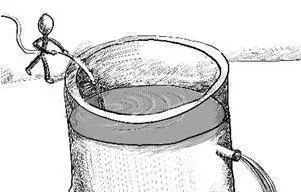
生物犹如的水缸

现在，根据克莱伯定律，代谢率即流入量与体重的 3/4 次幂成正比，而流出量即生物体用于修复自身细胞消耗的能量与体重成正比。尽管在一开始流入量大于流出量，促进了生物体的快速成长、发育，但随着体重本身的增加，流入量的增长速度会慢于流出量的增长速度（3/4 小于 1），这就是生长速度的错配。因而必然会有这么一个时间点，流入量刚好与流出量持平，生物体不再生长。

应用类似的生长速度错配的原理，我们还能推导出哥斯拉这样的超级巨兽是不可能存在的。因为它体重的增长速度是身高的 3 次方，而它的腿骨所能承受的支撑应力会随着身高的 2 次方增长，3 次方显然快于 2 次方，所以必然有这么一个规模点，哥斯拉自身的体重就会把自己的腿骨压断。

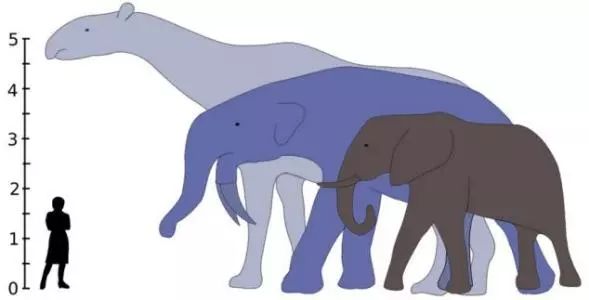
陆地动物的规模尺度

尽管城市的生长与生物体的生长遵循数学形式上一模一样的方程，但由于城市的新陈代谢遵循超线性规模法则，城市呈现出了超指数增长——比指数增长还要快很多的一种生长模式，与生物体的受限生长简直就是大相径庭。理论还预测，城市会在有限的时间点达到无穷的规模。这意味着什么？根据规模法则，社会财富、创新伴随着犯罪和污染会以相同的速度趋于无穷大，我们进入了一个天堂与地狱混合的奇怪世界。

然而，为什么我们从来没有观察到这样的现象呢？韦斯特给出的解释是，科技创新可以让城市生长偏离既定的超指数生长轨迹，颠覆原有的社会经济生态，从而“重启”整个动力学过程，让整个城市进入另一个方程相同但参数不同的新动力学过程。尽管新的生长过程仍会趋于超指数的临界点，但它又会被另一次重大科技创新“重启”。这一过程会一直持续下去。这也就是经济学家熊彼特所说的颠覆式创新与超周期发展规律。

但是，故事还没有结束。理论预测整个过程会以越来越快的速度持续进行下去。用韦斯特的话来说，我们不仅早已踏上了一台永不停止的跑步机，而且还会不断跳到另一台速度更快的跑步机上。整个过程都在以指数的方式加速：虽然科技创新能够一次次地解决原来超指数增长的问题，但是它不得不持续加速下去，从而导致任意两次重大科技革命之间的时间间隔不断缩短。我们的确体会到了这样的过程：人类用了将近 20 年才完成互联网革命，却用了短短的 5 年时间就已经完成了移动互联网革命。

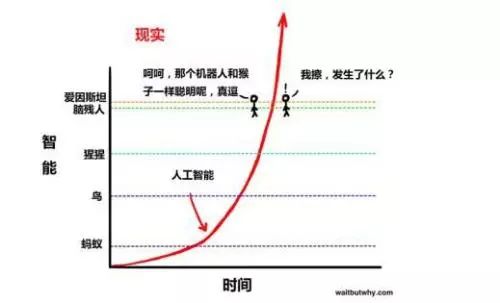
人工智能的加速列车

持续的指数加速必然会让人类进入一个不可避免的时间点——奇点。我们都知道，技术奇点这个概念最早是由美国数学家和小说家弗诺·文奇（Vernor Vinge）提出并由美国发明家、预言家雷·库兹韦尔（Ray Kurzweil）发展与扩散的。他们根据摩尔定律进行外推，计算出奇点的准确时间就是机器的计算能力超越人类的那一刻。然而，这种能力的预估存在很大的争议。

非常有意思的是，韦斯特采用了完全不一样的框架，即通过超线性规模法则和生长方程也得出了相类似的奇点概念。

奇点临近的时候会发生什么？韦斯特对此报以悲观的态度。不要希冀科技创新，它不是永远的灵丹妙药。与创新相伴而生的魔鬼——犯罪、污染等灾难会让人类社会进入一个崩溃的阶段。这恐怕是本书揭露的一个最让人沮丧与担忧的问题。

内在网络一个理论不仅要展现数据，而且要给出机制性的解释。

为什么规模法则具有高度普遍性呢？韦斯特给出的回答是，所有这些我们关心的复杂系统背后都存在类似的网络，动物体内存在血管网络，植物体内存在经脉网络，城市内部存在公路网络，公司内部存在通信网络，在线社区上存在社交网络，这些网络的共性即普遍存在的规模法则。

如果你透过飞机的悬窗俯瞰夜晚的城市，就会发现道路网络像极了人体内的血管，其中主干道路就像大而粗的主动脉，大量小路就像毛细血管，奔驰的汽车就像血液。

对生物体来说，韦斯特和他的合作者提出了著名的网络模型，剖析了所有生物体背后普适的分形输运网络。大自然的进化迫使这些网络不断优化自身，使其不断分叉、卷曲，甚至硬生生地“逼迫”出一个全新的维度出来。有了这个全新的维度，生物体就可以最大限度地利用它内部褶皱的表面去吸收营养物质以使它自身的新陈代谢效率最大化。为什么生物体的规模法则中都存在那个神奇的数字“4”呢？这是因为所有生物体都像生活在一个四维空间中。

同样的道理，城市、人类组织，甚至在线社区中普遍存在的超线性规模法则背后也是不变的基础设施网络或社会关系网络。

早在 300 多年前，亚当·斯密就提出了“大头针工厂”之谜：在人们按照各自的角色社会分工之后，工厂整体的工作效率会远高于所有工人独自工作的效率之和。其实，社会分工和合作就是在形成人与人之间的交互网络。正是因为人与人之间的互动会随着人数的增多而呈现更快速的增长，才会出现普遍的超线性增长规模法则。

例如，如果社会中任意两个人之间可以发生随机联系的话，那么可能的连接数就会以人数的平方倍数增长，这已经体现了超线性的增长。只不过城市、在线社区等系统中的真实指数并非 2，而是大多介于 1~2 之间，这说明现实的人类并不会任意相互联系，而会受到各种各样的约束，从而使得连接数的增长快于线性增长而慢于平方增长。

圣塔菲研究所的路易斯·贝当古（Luis Bettencourt）等人的研究就指出城市中的人只能在道路这一“城市界面”上发生连接，故而城市中普遍存在 1.15 次幂规模法则。我与北京师范大学系统科学学院的李睿琪和王文旭等人，以及香港城市大学的吴令飞的研究表明，城市及在线社区的生长还受限于其生长的方式，即一个新成员的加入必须要与老成员相互邻近，于是给出了 GDP（国内生产总值）、创新等指标的1.15次幂规模法则的不同解释[④]。这里的邻近可以是真实的地理空间邻近，也可以是人们头脑中的兴趣空间邻近。

然而，我们现在取得的成绩还远远不够。我们呼唤新时代的牛顿。

下一个牛顿会是谁？

1601 年的某天晚上，丹麦天文学家第谷·布拉赫（Tycho Brahe）撒手人寰，把自己长达20 多年来积攒的行星运行数据留给了助手约翰尼斯·开普勒（Johannes Kepler）。经过 20 多年的探索，开普勒终于将这大量的数据总结提炼成精确的方程，即开普勒定律。又过了 20 年，牛顿站在开普勒、伽利略等巨人的肩上，提出了万有引力定律和牛顿运动定律。至此，经典力学革命爆发。牛顿力学与开普勒定律的本质区别在于后者的应用范围仅仅局限于太阳系，而前者的适用范围则包括了宇宙中的一切具备质量的宏观物体。这就是定律（law）与力学（mechanics）的区别。

“mechanics”在英文中不仅有力学的意思，而且包含了事物背后的运行机制和基本原理。我们今天所面临的局势很像当年开普勒所面临的。随着大数据的发展，我们已经积累了有关生物体、城市、公司的大量有价值的数据。克莱伯定律等规模法则的提炼则可以类比为开普勒的发现，这些实证规律清晰地向我们揭示了复杂系统背后的统一性和规则性。然而，再多的实证统计规律都无法与一条清晰、简单的力学原理相媲美。我们呼唤新时代的牛顿。

有人认为大数据、人工智能时代将不会再次重复牛顿时代的英雄故事，我们不需要理解事物背后的基本原理和因果关系，单纯地依靠大数据的模式挖掘就能解决所有复杂问题。物理学家出身的韦斯特却并不这样认为，“大数据时代更需要大理论”，他一针见血地指出了当前大数据、人工智能研究范式的弊端。如果没有对事物运行背后的力学机制的基本思考，我们就很容易误入歧途，浪费大量的算力。

这就是《规模》背后的基本精神和态度，追求至高无上的基本原理和逻辑框架，而不是随波逐流。它就像注入人工智能时代的一股清流。

[①] 1 英寸 =2.54 厘米。——编者注

[②]LingfeiWu, Jiang Zhang: Accelerating growth and size-dependent distribution of humanonline activities; Physical Review E84, 026113, 2011.

[③]Lingfei Wu, Jiang Zhang, Min Zhao: TheMetabolism and Growth of Web Forums; PLoSONE 2014, 9(8): e102646.

[④]RuiqiLi, Lei Dong, Jiang Zhang, Xinran Wang, Wenxu Wang, E.G. Stanley: Simplespatial scalingrules behind complex cities; NatureCommunications 8, 1841 (2017), Jiang Zhang, Xintong Li, Xinran Wang,WenxuWang, Lingfei Wu: Scaling behaviours in the growth of networked systems andtheir geometricorigins; Scientific Reports 2015, 5: 9767.