导语

少数人能改变社会习俗吗？临界点理论模型显示，社会中的少数群体可以引发社会变化，产生新的社会习俗。在最新一期《Science》中，研究者通过网络社区实验，发现在系统中的个体会互相作用并建立新的平衡，并且存在一个改变“社会习俗”的临界点。

1.只要人数超过临界点，小团体也能改变社会习俗

临界点理论模型显示，社会中的少数群体可以引发社会变化，产生新的社会习俗。在此我们对社会习俗的人工系统进行了研究，发现在系统中人类会互相作用并建立新的协调平衡。我们的发现为“社会习俗变革动力学中临界点的存在”提供了直接的实证证据。

临界点就是发起社会变化的群体规模，当少数群体达到此临界点，既有社会行为就会被颠覆。社会行为被颠覆的临界值大小根据特定社交场合的理论可识别特征的变化而变化。研究结果表明，理论上预测的临界点确实会在社会协调系统中出现。

社会习俗迅速变化的实证研究表明，看似稳定的社会规范可以被少数群体有效地推翻[1-3]。从对工作场所性别角色的社会期望，到对烟草和大麻的普遍接受程度，我们假设少数群体可以触发由大多数人所持有的社会习俗的改变[1-3，5，6]。

尽管这一假设与经济学理论中的经典均衡稳定性分析的期望存在天壤之别[7，8]，但我们不能用进化博弈论中的临界马斯拉斯理论来对其进行一个很好的解释[9-11]。这一理论认为当少数群体的规模达到我们所称的临界点时，社会系统也会达到一个所谓的临界点。而一旦达到这个临界点，少数群体的动作行为会触发行为变革的级联效应，从而快速增加少数群体的认同感[12-14]。

临界点理论中，最简单的方法就是保持社会的各个小群体拥有一样的社会力量以及社会资源，这样就可以成功引起社会习俗的改变。据此可以看出，小团体的力量并不来自他们的权威或财富，而来自他们对事业的奉献[14，15]。

到目前为止，关于社会习俗变化中临界点的变化，只可在其理论模型和定性研究的观察中得到证明。这些研究已经提出有效临界点的可能阈值变化范围，从总人口的10%到40%不等。例如，有关语言习俗的理论仿真研究表明，占总人数10％的临界规模就足以推翻现有的社会均衡态[14]。

相反，在对领导角色性别相关的问题进行定量研究时，可以发现这一值达到了30%[3，16]。建立在该研究基础之上的其他一些有关性别习俗的观察性工作[17]据此推测，其有效的临界群体规模可能更大，达到人口数目的40%。尽管对集体行为中临界点动力学的理解具有其实践[18,19]和科学[1,12]意义上的重要性，但是这并不能证明在现实社会中也存在临界点。因为这样的实验需要在不断发展的社会协调体系内分别改变各个少数群体的规模大小以进行研究。

临界群体

我们通过采用实验性的方法，在人为创造的不断演变的社会习俗体系内对临界点动态问题进行了研究，回答了现实社会中是否存在临界点变化的问题。根据社会习俗的相关文献[9,20,21]，我们对一个少数群体的行为者试图破坏既定均衡行为的协调系统进行了研究。

在我们的理论框架和实证研究中，采用了规范的方法，将命名约定中的协调作为常规行为的一般模型[21-24]。我们的实验方法旨在对现有关于社会习俗临界点问题的文献中得出的广泛理论预测进行测试与验证。

我们首先综合临界点变化的各种理论和观测说明，来推导出有效临界点的理论预测[25]。基于之前的理论[9，26]以及关于社会习俗的定性研究[20，23]，我们提出了一个策略选择的简单模型。

该模型中，社会成员根据他们以往在社会中的互动，选择可能产生最大个人预期的选项，进而来决定遵循哪种社会习俗。在这个个体学习模型中，人们在协调中互相帮助，和谐相处。该模型预测，当少数群体占总人口比重达到临界点时，社会习俗会发生较大转变（如图1）。当少数群体占总人口比重小于预测的临界点，现有主流社会习俗会保持稳定，超过这个点则会发生社会变革[25]。

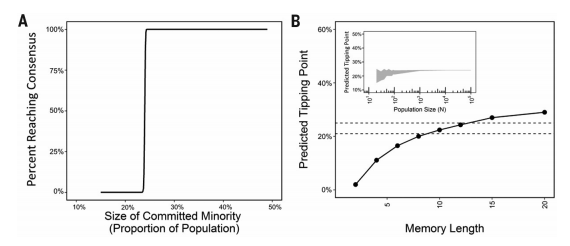
图1 社会稳定性的临界点预测。

（图A横坐标为少数群体的数量大小（占总人口比重），纵坐标为达成社会共识的比例）

（图B横坐标为记忆长度，纵坐标为预测临界点）

（A）替代社会习俗被100%社会人口所接纳时的理论模型。在这个系统中，社会主体数量为N=1000，发生的相互交流数量为T=1000，过去发生的相互交流数量为M=12。

（B）预测临界点的值被绘制成为关于平均记忆长度的函数曲线（其中N=1000，T=1000）。虚线表示我们实验的结果范围，展示了发生社会变革时少数群体的最大比重（21%）与最小比重（25%）。虽然预测的临界点大小会随着M的增大而增大，但该曲线为凹曲线，所以也使得预测的临界点在M>100时仍小于50%。附图为增加人口规模对少数民族。

（C）预测规模的精确度影响（M=12,T=1000）。当N<1000时，预测的临界点会产生微小波动，这主要是由于个人行为的随机波动而产生的。阴影部分指成功观察到的C值的大小，但没有确定值。在阴影部分之上，C值的数量更大，社会变革成功的概率趋近于1；C值在这个区域之下，变革成功的概率为0。

我们对于临界点的理论预测有两个参数决定：记忆长度M和社会人口数量N。针对两个参数的研究如图1所示，可以看出预测的临界点的大小随着社会成员的预期记忆长度的改变而改变。当参与者的记忆长度M<5时，临界点较小。即便在记忆长度较大，M>100时，临界点仍小于总人口数量的50%。这一结果表明：在一个拥有悠久历史的社会体系中，临界点仍有发生改变的可能性。

当人口数量N在20-100,000时，预测的临界点不会发生太大的变化。图1展示了在对人口数量N在20-1000的社会进行临界点的预测时，引入微小不确定量所带来的随机波动。然而，当社会人口数量N>1000时，预测的临界点值趋于稳定，并且不受N取值大小的影响（具体见文献25）。

2.网络社区实验：超过25%就能引起改变？

我们从网络上招募了194个志愿者并将他们置于网络社区，参与社会协调的过程[27，28]。

网络社区的随机配对

研究中，参与者被随机分配到10个独立的线上小组之一，各小组的规模在20-30人不等。在给定的轮数中，每一小组的成员都会被随机配对并彼此互动。我们让每一对成员同时对一个物品进行命名（例如脸），尝试在即时语言选择中进行协调[20，25]。如果成员输入的名称相同（例如协调），他们会成功得到相应奖励，否则就会受到惩罚。在每一个社区中，每个成员进行多轮随机组合配对，旨在彼此互动并互相协调。

实验中，我们不会激励成员去达到某项全局共识，而只是在每一次的配对中去与配对者进行协调，达成一致。他们会在协调成功或失败的情况下得到奖励或惩罚(25)。一旦在全体人民中建立了一项公约或形成了一套习俗，人们会倾向于协调均衡行为。

每一轮配对之后，参与者只会看到自己和配对者的选择，他们累计获得的奖励也会相应更新。他们之后会被安排同社区内其他新的参与者进行随机分配和互动，进入下一个新的回合。

这些动态反映了常见的在线交流类型，其中社区成员直接与大多匿名人群中的其他成员进行互动，利用聊天工具，引导他们接受社区的语言与行为习惯，使他们的语言与行为与其他参与者的预期一致[20，29，30]。

与设想的一致，研究中的参与者并不知道社区人口的数量，也不知道与谁发生了联系[9，20，23]。在每一个小组中，互动过程很快就导致了小组范围内习俗的形成，小组中所有成员行为都一致[20，25]。一旦小组中的习俗被建立起来，我们就会引入一小部分的同盟者（这就是少数群体），他们会尝试用另外一种习俗推翻已有习俗[25]。

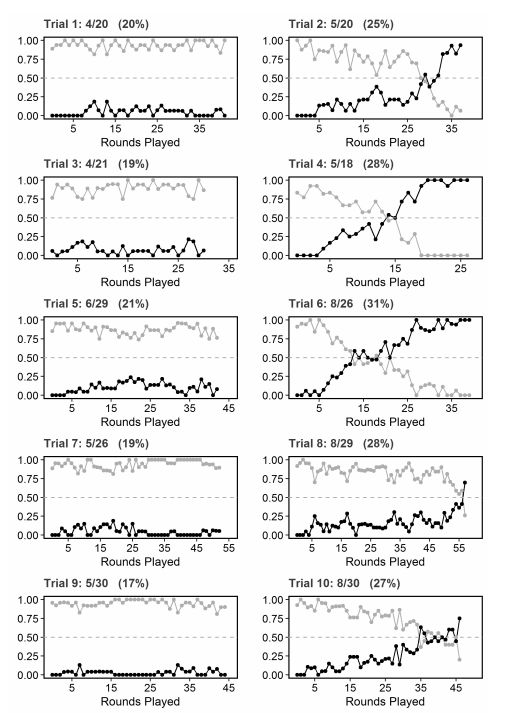
图2 社会习俗接纳程度随时间的变化（例如实验对象）

灰线表示已建立习俗的普及率；黑线代表替代习俗。当超过50%的社会人口接受了新的社会习俗，就意味着实验成功。

图中第一列展示的是失败的社会动员，第二列展示的是成功的社会动员。当C到达社会人口的25%时，社会习俗会发生变化。实验中每一轮配对都有N/2次的两两相互作用，即在每一轮配对中，成员都有一次互相交流。

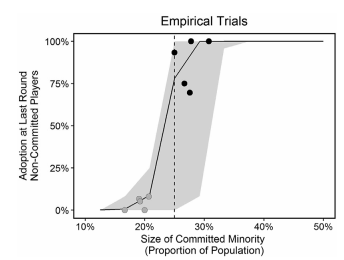
图3 从所有实验中得出的最终结果

（横坐标为少数群体数量（占总人口的比重），纵坐标为最后一轮实验的接受程度）

（灰色的点表示在C<25%下的实验，黑色的点表示在C>25%下进行的实验）

还显示了具有95％置信区间的理论预测的临界点，实线所示，其中N=24，T=45，M=12。灰色区域表示1000次重复实验的95％置信区间。点划线表示C=25%。此临界点理论模型提供了一个很好的实证结果近似。

在短时间周期内（T<100个相互作用），临界点预测不是特别准确（C在20%到30%的范围内变化）；但是当T>1000，临界点的预测就比较准确（实线，25）。

实验结果伴随试图推翻已有社会习俗的少数群体规模（C）的变化而发生改变。总的来说，我们研究了10个独立组的临界点变化，每个组都有一个固定大小的少数群体。在所有10个组中，所有少数群体的人数都在（15％<C <35％）范围内。

图2和图3展示了推翻已建立均衡过程中临界点的变化情况。由图可知结果符合我们理论模型的预期（N和M使用了经验值），当少数群体的规模达到社会人口的25％时，临界点被触发，少数群体成功改变既定的社会习俗。

对五组实验进行了统计。每一组实验有两个团体组成，一个团体的少数群体人数占总人口比重C<25%，另一团体的少数群体人数占总人口比重C>25%。每一组实验中，C<25%的团体中只有小部分人关注少数群体的观点。在这些实验的过程中，少数群体中的每一个成员最终都回归到了主流社会习俗上。整个研究中，持续的相互作用会产生临时的社会习俗变化。然而，在所有试验中，在少数群体人口少于25％的情况下，平均只有6％的少数群体在实验的最后一轮采用了新的社会习俗。

我们对另一个拥有相同规模，但少数群体占比（25％≤C≤31％）大一些的团体进行了相同的实验。在此实验中，新习俗被团体中的大部分人认可（图2和3）。所有试验中，C≥25％的团体较之25％以下的团体，主流习俗更易被推翻（P = 0.01，秩和检验）。我们发现在一个案例（实验1）中，新习俗由不被认可到被认可的过程，仅仅是因为在少数群体中增加了一个人。

多一个人点亮新习俗

图3显示了所有实验中对最终社会新习俗的接受水平进行了总结，以及使用了经验值的理论模型的期望值，其中期望值的置信区间为95%。具有25％≤C≤27％的少数群体的社会团体中，在实际观察结果中，对于新习俗的接纳水平在72％到100％之间。在C = 31％时，少数群体在实际观察结果中，发现可以100%达成新的社会共识。

图3将理论模型的数值模拟观察结果与实际研究（N = 24，T = 100，M = 12）的观察结果（T轮相互作用）进行比较。模拟的记忆长度根据参与者在所有10组中观察到的行为，使用参与者的实际记忆长度来校准。

在9≤M≤13范围内，模拟的记忆长度与实际相似。实验中，理论模型成功预测了团体成员80％的选择[25]。理论预测的该模型的临界点很好地符合实验结果（图3）。数值分析表明，在人口规模较大的情况下，临界点预测更加准确（见图1和3），达到接近24.3％的人口。

3.深入思考：真实世界或许更保守

我们的实验结果没有展示社会习俗预测模型在低阈值情况下的结果，即少数群体占社会总人口的10%这一情况。然而，我们的发现与性别相关习俗定性研究却有高度一致性[3]。在对性别相关习俗定性研究中，假设了少数群体达到社会总人口的30%，就足以推翻现有习俗[16]。我们的发现与这一研究十分吻合。我们的研究结果表明，在群体边界相对清晰，对同伴之间的社会协调有明确期望和回报的组织背景下，社会习俗中的规范性变化的过程可以通过临界点变化来描述。

我们的实验设计既有助于对研究过程的控制，同时也对所测试的行为进行了限制。实验中，我们用社交和经济激励去促使在一个社会团体内建立社会习俗[25]。但在真实世界中，个体对已形成行为在情感和心理上的认同可能会对他们行为改变产生额外的阻力[31]。

从无到有，广场舞是如何流行起来的？

对这些结果期望值的进一步深入探究，则需对我们的理论模型进行补充分析，在考虑更多社会防护下临界点如何变化的情况下，来扩展我们已有及基本结论（图s7）[25]。社会成员越保守，越趋向于保留已有习俗（基于有利于均衡态行为的偏斜最佳响应计算），但临界点的变化仍可以根据稍大规模的少数群体来进行预测。

在界定我们发现的适用范围方面，我们强调25%这一临界点数值并不普遍适用于社会习俗的改变。结果表明，在内生的社会协调体系中，转折点的变化始终与理论预期一致。我们需要做更多的工作使我们的发现可以应用在更多的特定社会系统中。特别地，我们的模型适用不同的经验参数，可以进行不同的临界点值预测。我们希望从研究中得到的结果，未来可以在针对社会习俗的实证研究中得到进一步地扩展。

例如，可以利用这些研究结果，让同盟成员在网络中影响社会行为习俗和信仰，进而提高组织和政府的增长稳定性。

我们预计这种社交媒体空间将成为一个越来越重要的环境，我们的研究结果也将扩展到这一领域，以了解少数群体在转变社会习俗方面的作用。

同样，我们研究的结果也会应用在其他线上的临界点变化应用中，例如（i）关于脸书和其他网上论坛的文明标准[19，34]，（ii）关于青少年群聊中欺凌行为的接受度[35]，以及（iii）社交媒体中向陌生人分享内容的种类[36]，所有这些都被认为是由于一小部分人群的活动而表现出对常规行为变化的敏感性[19，34，36]。

4.引用与备注

[1] T. Kuran, Am. J. Sociol. 100, 1528–1551 (1995).

[2] K. D. Opp, C. Gern, Am. Sociol. Rev. 58, 659–680 (1993).

[3] R. M. Kanter, Am. J. Sociol. 82, 965–990 (1977).

[4] D. Dahlerup, L. Freidenvall, Int. Fem. J. Polit. 7, 26–48 (2005).

[5] S. Bikhchandani, D. Hirshleifer, I. Welch, J. Polit. Econ. 100,992–1026 (1992).

[6] T. Kuran, Private Truths, Public Lies: The Social Consequences of Preference Falsification (Harvard Univ.Press, 1997).

[7] J. C. Harsanyi, R. Selten, A General Theory of Equilibrium Selection in Games (MIT Press, Cambridge, 1988).

[8] J. F. Nash, Proc. Natl. Acad. Sci. U.S.A. 36, 48–49 (1950).

[9] H. P. Young, Econometrica J. Econom. Soc. 61, 57–84 (1993).

[10] M. Kandori, G. J. Mailath, R. Rob, Econometrica J. Econom. Soc.61, 29–56 (1993).

[11] G. Ellison, Econometrica J. Econom. Soc. 61, 1047–1071 (1993).

[12] T. Schelling, Micromotives and Macrobehavior (Norton,New York, 1978).

[13] M. Granovetter, Am. J. Sociol. 83, 1420–1443 (1978).

[14] J. Xie et al., Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 84,011130 (2011).

[15] D. M. Centola, Ration. Soc. 25, 3–40 (2013).

[16] D. Dahlerup, Scand. Polit. Stud. 11, 275–298 (1988).

[17] S. Grey, Polit. Gend. 2, 492–502 (2006).

[18] G. Marwell, P. Oliver, The Critical Mass in Collective Action

(Cambridge Univ. Press, 1993).

[19] K. Nyborg et al., Science 354, 42–43 (2016).

[20] D. Centola, A. Baronchelli, Proc. Natl. Acad. Sci. U.S.A. 112,

1989–1994 (2015).

[21] D. Lewis, Convention: A Philosophical Study (Harvard Univ.

Press, Cambridge, 1969).

[22] C. Castellano, S. Fortunato, V. Loreto, Rev. Mod. Phys. 81, 591

(2009).

[23] S. Garrod, G. Doherty, Cognition 53, 181–215 (1994).

[24] L. Wittgenstein, Philosophical Investigations (John Wiley & Sons,

2009).

[25] Materials and methods are available as supplementary

materials.

[26] A. Baronchelli, M. Felici, V. Loreto, E. Caglioti, L. Steels, J. Stat.

Mech. Theory Exp. 2006, P06014 (2006).

[27] D. Centola, Science 334, 1269–1272 (2011).

[28] D. Centola, Science 329, 1194–1197 (2010).

[29] L. Backstrom, D. Huttenlocher, J. Kleinberg, X. Lan, Group

formation in large social networks: membership, growth, and evolution. Proc. 12th ACM SIGKDD Int. Conf. Knowl. Discov. Data Min., 44–54 (2006).

[30] F. Kooti, H. Yang, M. Cha, P. K. Gummadi, W. A. Mason, The Emergence of Conventions in Online Social Networks. Proc. Sixth Int. AAAI Conf. Weblogs Soc. Media ICWSM 2012 (2012).

[31] C. Tilly, S. Tarrow, Contentious Politics (Oxford Univ. Press, New York, ed. 2, 2015).

[32] G. King, J. Pan, M. E. Roberts, Am. Polit. Sci. Rev. 111, 484–501 (2017).

[33] G. King, J. Pan, M. E. Roberts, Science 345, 1251722 (2014).

[34] A. Antoci, A. Delfino, F. Paglieri, F. Panebianco, F. Sabatini,PLOS ONE 11, e0164286 (2016).

[35] E. L. Paluck, H. Shepherd, P. M. Aronow, Proc. Natl. Acad. Sci. U.S.A. 113, 566–571 (2016).

[36] C. Shih, The Facebook Era: Tapping Online Social Networks to Market, Sell, and Innovate (Pearson Education, 2010).