1.数学模型破解公司组织层级难题

2.组织层级管理的三个基本原理

3.随着团队规模扩大，沟通成本快速增加

4.管理中的规模法则：管3-4个人最合适

5.哪些因素影响着一个层级组织的产出

6.理论指导实践一：该不该扁平化管理

7.理论指导实践二：大公司该不该将业务拆分

8.人工智能会怎样冲击未来的组织

1.数学模型破解公司组织层级难题

韩信将兵多多益善，这话说起来容易，但真要你穿越到韩信的位置上，多半会焦头烂额。不过经过现代科学思维训练的你，会想起“数学模型”这个神器。不论是管理一只几十万人的军队，还是一个几百人的企业，都需要靠是层级化的组织。那在不同的环境下，什么才是最优的组织架构层次？

近期发表在 PLOS ONE 的一篇论文，提出了一套通过配置层次化组织，以使得组织产出最优化的模型。通过该模型，我们可以估算什么样的企业适合扁平化管理、一个大组织在什么情况下需要打散成小团队。

论文题目：

A Theory of Discrete Hierarchies as Optimal Cost-Adjusted Productivity Organisations

论文地址：

https://journals.plos.org/plosone/articleid=10.1371/journal.pone.0214911

对于管理而言，没有最优解。这项研究中考虑到了社交互动与组织生产的几个核心影响要素，给出了不同条件下的合适方案建议：

什么样的组织是否适合扁平化管理？

管理者决策能力越强，越应该把组织层级压低。而对不同组织的不同阶段而言，随着层级扩张，沟通成本的增长速度是不同的。如果随着层级扩张，沟通成本的增长速度较慢那么这样的组织也适合扁平化的管理。

什么情况下大组织应拆分成多个小团队？

如果一个团队的产出，不会随着团队成员的增加而产生超线性的增长，那么保持严密的层级化组织就是不合算的。在这样的情况下，除非管理者的领导能力非常强，否则就应该把大团队拆分成多个小团队。

2.组织层级管理的三个基本原理

群体协作既可能带来增益，又可能带来损失。信息在层层传递过程中会逐渐失真，进而带来组织产出的降低；而双剑合璧，组成小群体，就能发挥出超越他们各自水平之和的战力。模型一定要能解释这样的两个方向相反的趋势。

这两个相互矛盾的事实将成为模型的基石。人类在进化的过程中演化出的社交能力决定了，特定结构大小的群体行动，既能够享受增益，又能避免过多人交流带来的损耗。进化给了我们的认知能力设定了极限，不论是什么原始社会还是现代社会，一个人能够直接照顾的社会关系约为150人，这就是邓巴数。而好的组织结构模型也要能解释邓巴数。

邓巴数，也称150定律，指能与某个人维持紧密人际关系的人数上限，通常人们认为是150。

对于组织层级管理而言，其数学建模基于以下三条基本原理：

合作带来的生产增益以指数化增加
沟通协调的成本与团队大小的平方成正比
不同层级对生产与沟通给予的权重不同

从这三点出发，研究者选取并抽象出重要的因素，作为模型中的实体，一步步地构建模型，来描述组织的层级规模及其生产力之间的关系。

3.随着团队规模扩大，沟通成本快速增加

假设群体中有N个人，每个人的产出是1，N个人的产出是N的β次方。对于小的组织来说，这里的β是大于1的，这会造成1+1大于2的超线性增长。但当一个组织达到30-50个人的时候，再增加人员就无法带来之前一样的正面增益了，这时β就小于1，增加人员投入不再为组织等比例地增加收益。

沟通成本的增加比人员数量的增加要快。因为每增加一个人，新增加的成员在与他人合作之前先要了解他们，这使得总的沟通成本达到了N×(N-1)，是以N的平方级别增加的。基于此，给定小团队的团队增益β，在群体不使用层级管理策略时的团队产出，可以这样建模：

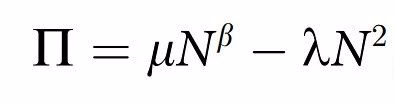
其中的 μ 和 λ 是两个为正的常数参数，分别为生产系数和沟通系数。想知道最优化产出Π的条件下N的值，在方程两边分别求导。N（代表最优产出时团队的大小）的取值为下：

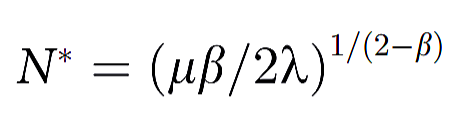
如果以邓巴数150，作为最优产出时的团队大小N*，假设β是1.5，那μ/λ 约等于16。对于一个每周工作40小时的员工，每周花2.5小时（40/16=2.5）在各种会议沟通上，这和日常生活经验相仿。

4.管理中的规模法则：管3-4个人最合适

需注意，我们讨论的重点是层次化的组织，用数学的语言翻译下，就是将N个人分成N1个组，每组N0个人，而总的沟通成本是N02*N1+N12。要想最优化沟通成本，需要N正比于N1/3, N₂ 正比于N2/3，此时总的沟通成本C正比于N4/3。

熟悉幂律法则的读者能想起在生物界再常见不过的3/4次方幂律关系。大多数哺乳动物，其体重与代谢率之间都存在3/4的幂次关系。同样的道理，在人类世界则是一个排长管3个班，一个连长管3个排，要想保持最优管理，一个人的直接领导的人应该是3-4个。

补充阅读：

生物大小、城市规模、公司寿命，背后竟然遵循同一套规模法则

社群发展的底层逻辑：匹配生长模型

5.哪些因素影响着一个层级组织的产出

从这里出发，我们可以描述具有层级结构的组织的总产出：

全文的核心公式

其中的qr代表了在这一层次，每个管理者管了多少人。括号中表示总产出减去沟通成本。乘号前代表每组的产出，乘号后面表示分成了多少组。

对于层次化组织而言，处在不同的层次，所需的沟通系数和生产系数会随着层级的高低而变化，所以需要在模型中引入生产系数μr=ωκr，和沟通成本λr=ρr 两个变量，来代替只有一层的情况下的常量沟通系数λ和生产系数μ。

这里的k和ρ分别代表生产系数与沟通系数随着层次结构变化而带来的变化。如果k>1，说明越是身居高位，生产力的提升越明显。而ρ>1时，则表示随着人员层级上升，沟通所占的时间的比重在升高。

模型参数一览：

N：组织的人员总量

p：组织的层级总数

q：某一层级中，一个管理者所管理的人数

r：组织的某一个层级

β：随着团队人员增加，团队产出的增益系数

λ：沟通成本系数

μ：生产系数

ρ：不同层级之间的沟通成本的增益系数

k：不同层级之间的生产率的增益系数

ω：单个个体的生产力，ω也设定了生产力与沟通成本的相对强度

理论指导实践

6.理论指导实践一：

该不该扁平化管理

假设你是一家四千人企业的总裁助理，如今流行扁平化的组织架构，领导要求调研公司适不适合搞成扁平化。这时该怎么回答了？

为了进一步简化问题，假设只有基层员工创造价值，中间的管理层只会由于沟通协调带来额外的成本（论文中以军队等军事化管理组织为例，也就是真正产生价值（有战斗力）的只有基层士兵）。此时有生产系数μr= ωδr0，与沟通系数λr=ρr，其中的r0是每个基层员工的平均产出，ω相当于管理者所做决策带来的收益因子，管理者决策能力越强，则ω越大，ρ是不同层级的沟通成本增益系数。

有了上述模型，可以拿出下面这张图：

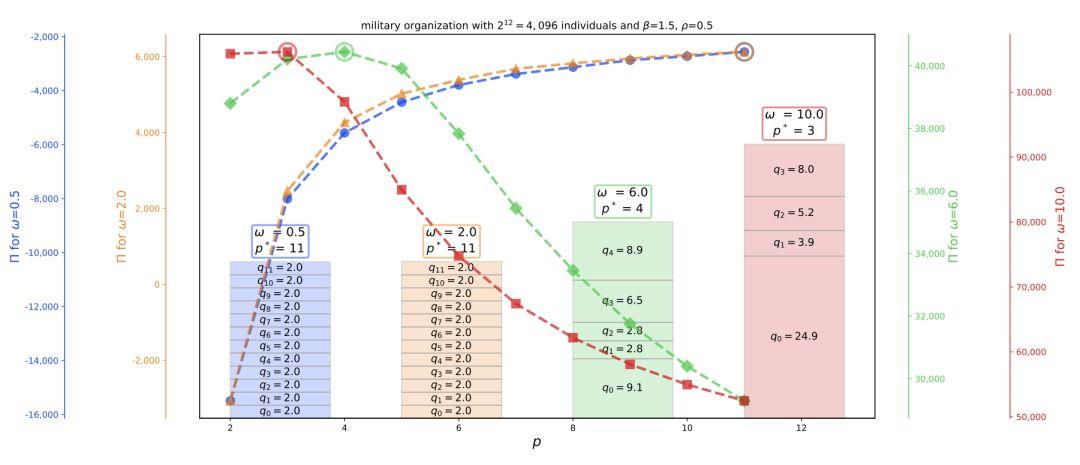
图中横轴表示组织层级数量，纵轴代表总产出，4 种颜色的曲线表示不同层级和参数下的层级-产出关系，其总产出值大小分别由4条不同颜色、不同尺度的坐标轴刻画。

假设该组织共 4096 人。该组织中，随着人员增加，生产力增加的增益系数β为1.5，不同层级之间沟通成本的增益系数ρ为0.5。层级为 12 层时达到一个极端，此时每层的领导只管着一个“士兵”，组织的总人数是 2 的 12 次方。在另一个极端层级为 2，是真正的扁平化，只有员工和大老板两层。

图中的蓝线代表着一个即将走向失败的组织，不管什么样的层次化结构，其总产出都是负的。根本原因是由于其ω<1，即外行领导内行导致的收益损失。对这样的组织，最优的管理结构就是12个层级，每层两个人。

橙色折线虽然和蓝色折线，都是在12时达到最高，而且最优的层级结构也是相近的。管理带来的收益乘数是ω=2，整个组织的总收益相比无论如何都无法持久的蓝线相比为正，但是沟通成本对应的系数ρ太高了，导致沟通成本高的扁平化管理会给企业带来压力，一旦将组织层级降低，整个组织的收益会变成负数。

图中的绿色和红色是适合扁平化管理的，而且ω越高，ρ越低，越应该把层次化组织压平。对红色组织而言，在最优情况下，第一层应该是平均24.9人，上面应该是3-4人，再往上升5-6人，而最高的一层是8人。但要适应这样的管理层次，需要管理者决策带来的乘数要达到11之高，且上位的管理者要沟通能力强。

所以，当大领导提问公司是否适合扁平化管理时，可以给出这张图和模型公式。是否适合扁平化管理，要看公司更接近那一个颜色。如果管理者有决断力，又擅长沟通，那确实应该扁平化，如果管理者个人领导力有限，那还是不要贸然减少组织架构的层次。

7.理论指导实践二：大公司该不该将业务拆分

最优组织层次模型不仅能解释一个企业在何时何地具有最优组织层次，还能决定企业该不该拆分某部分业务，无论是让其成为独立的子公司，又或者鼓励员工去创业。

假设你还是总裁助理，老板想知道哪些业务拆分后，公司整体产出更高，你仍然可以用本文的模型，给出下图：

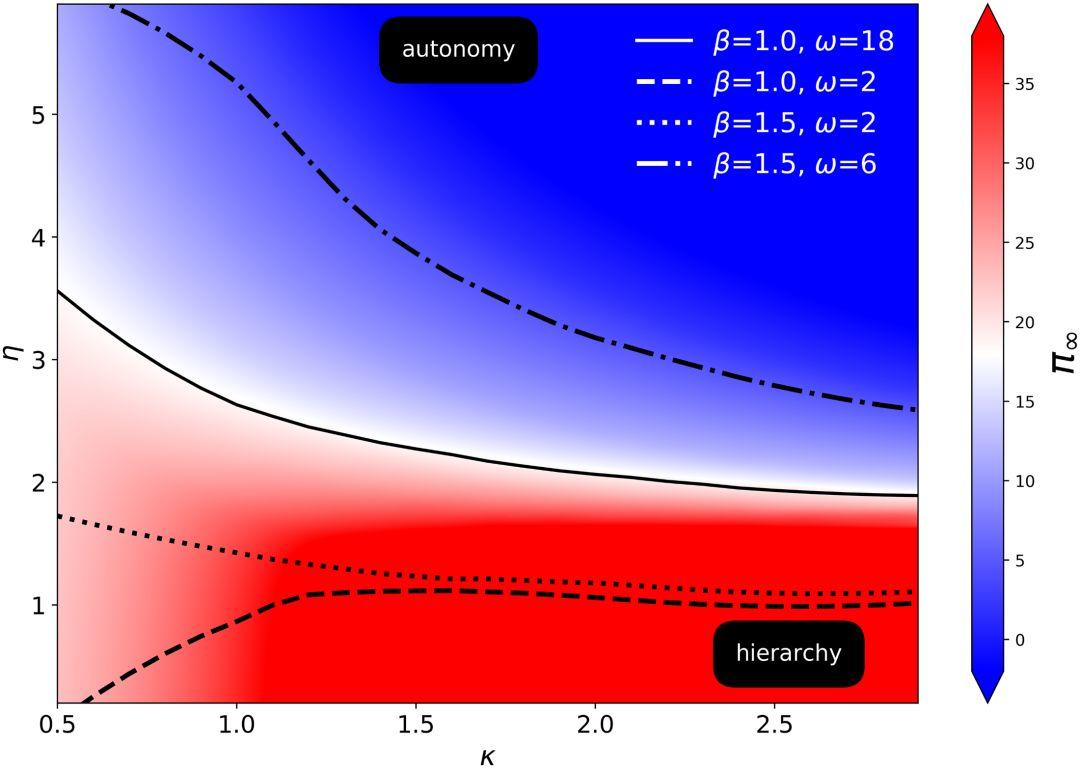
β代表团队合作带来的增益，ω是管理带来的增益乘数。

对整个组织的4096人进行了人均生产力的计算，随着层级间生产力增益系数k的增加，人均生产力趋于稳定。

图中有两个重点变量，其中的β代表团队合作带来的增益，ω是管理带来的增益乘数。在白色边界区域，扁平化和层次化的组织，每个人的人均产出是相等的；在红色区域，个人加入层次化的组织，能够提升人均产出，而蓝色区域则相反。图中不同的线型代表的是不同的β和ω值。

如果加入一个团队带来的产出增长，不会随着团队成员增长而产生超线性增长，那就不应该继续增加层级组织，而应该拆分。除非管理层的收益乘数很大时，此时仍应该保持层级化组织。而如果你从事的行业属于人多力量大的类型，即β>1，并且管理者的正确决策能带来个人产出的增长，此时单打独斗的收益是划不来的。有了这幅图，我们就可以区分出一个公司应该保留的核心业务，而将其他部门分拆出去。

8.人工智能会怎样冲击未来的组织架构

最后，我们回顾该研究的三条基本假设：