最近的一系列新证明，使理论计算机科学家离这个学科的一个伟大猜想更近一步。

1.向证明 UG 猜想更进一步

今年1月份在线发布的一篇论文，最近其他三篇论文结合在一起，使得UG猜想的证明向前迈出了实质性的一步。UG 猜想即 Unique Games Conjecture，该猜想是由纽约大学的计算机科学家 Subhash Khot 在2002年提出的。（注：UG 猜想提出时，Subhash Khot 正在普林斯顿大学攻读博士学位。）

UG 猜想的提出者：Subhash Khot

图片来源：Quanta Magazine

UG 猜想（是否存在某种对网络进行着色的有效方法）在过去的十五年中，这一猜想刺激了对泡沫几何（geometry of foams）和选举系统稳定性（stability of election systems）等多个话题的探索。 如果这个猜想能够得到证明，其含义将远远超出网络顶点着色（network-coloring）。例如有些问题，我们需要它满足尽可能多的约束条件，比如数独中的各种规则或一群婚礼嘉宾的座位偏好等，我们都能够找到这些问题的最优算法。

以色列威茨曼研究所的理论计算机科学家 Irit Dinur 认为：“如果这个猜想是对的，一大类着色问题的复杂度就能被很好地解释”。

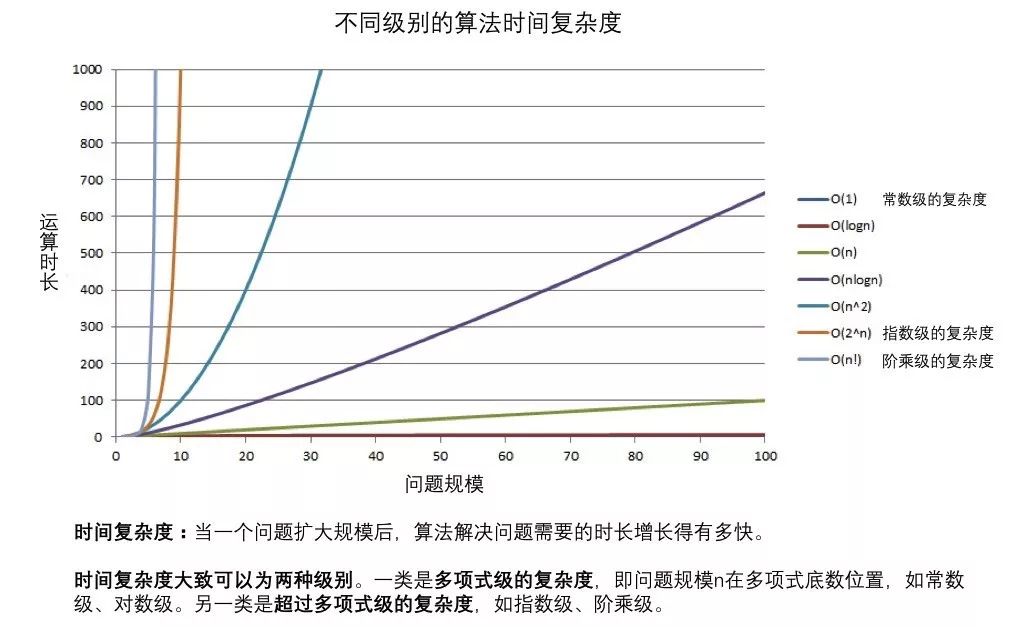
时间复杂度

然而，直到此论文发表之前，所有证明 UG 猜想的尝试都失败了。与此同时，计算机科学家还曾暗示这个猜想实际上可能是错误的。

Dor Menzer 说：“有些人认为，证伪这个猜想只是一个时间问题。”Dor Menzer 是以色列特拉维夫大学的研究生，同时与 Khot 和同校的 Muli Safra 教授一起是前面四篇论文的共同作者（他们三人与 Dinur 以及来自耶路撒冷希伯来大学的 Guy Kindler 共同撰写了其中的两篇论文）。

随着这项新工作的发表，旧有的思想似乎已经转变了。哈佛大学理论计算机科学家Boaz Barak 曾是这个猜想最激烈的怀疑者之一，但他说：“这是证明 UG 猜想正确性最有力的证据，这项工作振奋人心！”

哈佛大学理论计算机科学家 Boaz Barak

2.为计算复杂性寻找漂亮的解释

Khot 在构建 UG 猜想时（那时他还是普林斯顿大学的一名普通的博士研究生），他的脑海里一直有一个明确的目标：更好地理解“图着色”问题的计算复杂度。具体来说，就是对网络节点（按数学家的定义，或可认为是一个“图”中的“顶点”）进行着色，使其相邻的顶点不能同色。

理论计算机科学家已经知道，对于需要三种或三种以上的颜色进行着色的图来说，寻找最优着色方案(即使用最少的颜色进行图着色)的问题是 NP 完全的（NP-complete problem)。这是一大类计算复杂度问题，几乎所有的科研人员都认为，我们无法为其找到高效的求解算法。（当然，我们总是可以通过穷举的方法，来找到合适的着色方案，但是当要着色的图很大时，这样蛮力的算法是非常低效的。）

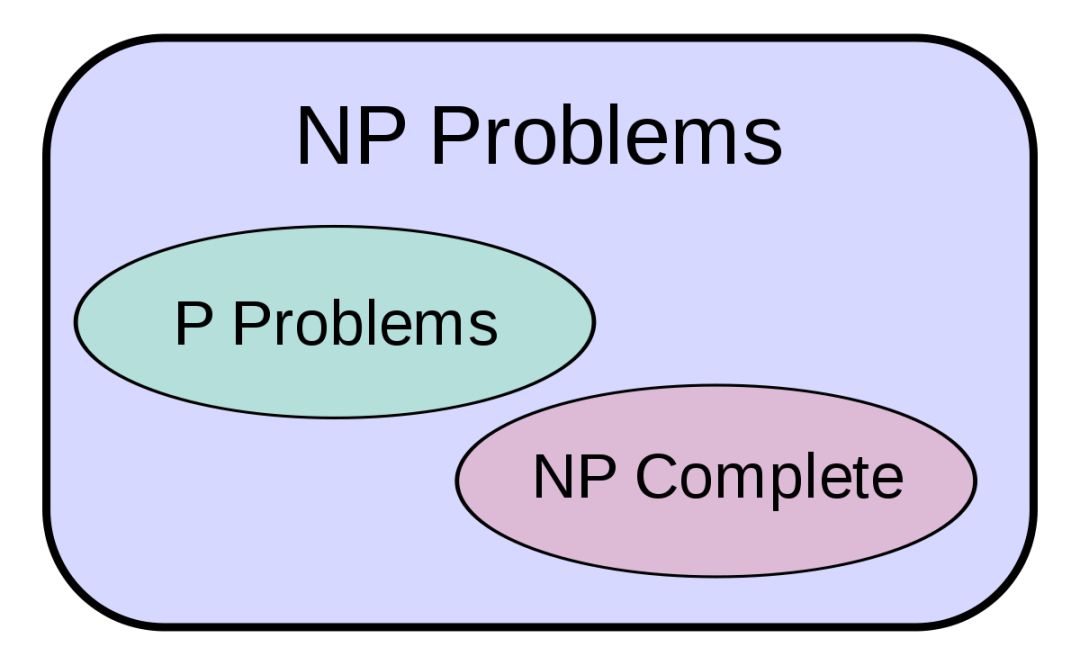
NP 问题、P 问题和 NPC 问题

P（Polynomially）问题：可在多项式时间内得解的问题。

NP 问题：不一定在多项式时间内得解，但可以在多项式时间内验证一个解的问题。只有 NP 问题才能找到多项式级的算法。

NPC 问题：所有 NP 问题都可以约化（Reducibility）到 NPC 问题。目前尚无多项式级的有效算法，计算的时间复杂度是指数级甚至是阶乘级的。

经典的图着色问题是一类 NP 完全问题（NPC 问题），没有多项式的有效算法。而对于 NPC 问题而言，随着问题规模增长，计算时长会呈指数级甚至阶乘级增长。

关于计算复杂度和 NPC 问题，可参考：http://www.matrix67.com/blog/archives/105

但如果你可用的颜色数量，比必要的颜色更多呢？比如你要处理一个用四种颜色着色的图，但你却可以使用100种颜色。你是否可以使用更大的颜色表，来有效地对这些图进行着色？ Khot 认为答案是否定的，但他还无法证明。

Khot 发现，解决 Unique Games 问题的关键，在于理解图着色的复杂度。图着色问题的目标，和 UG 问题一样，同样是为图中的点着色，但这个问题的规则更特殊：无论何时，为某个节点着色时，相邻的节点都必须使用某种特定的颜色。而 UG 问题中，相邻节点的着色规则可能会冲突（比如婚礼上的冲突的座位需求），所以，我们的目标是，找到一种着色方案，使之满足尽可能多的着色规则。（Unique Games 这个名字来源于博弈论中的一个类似的问题，而不是图着色的问题）

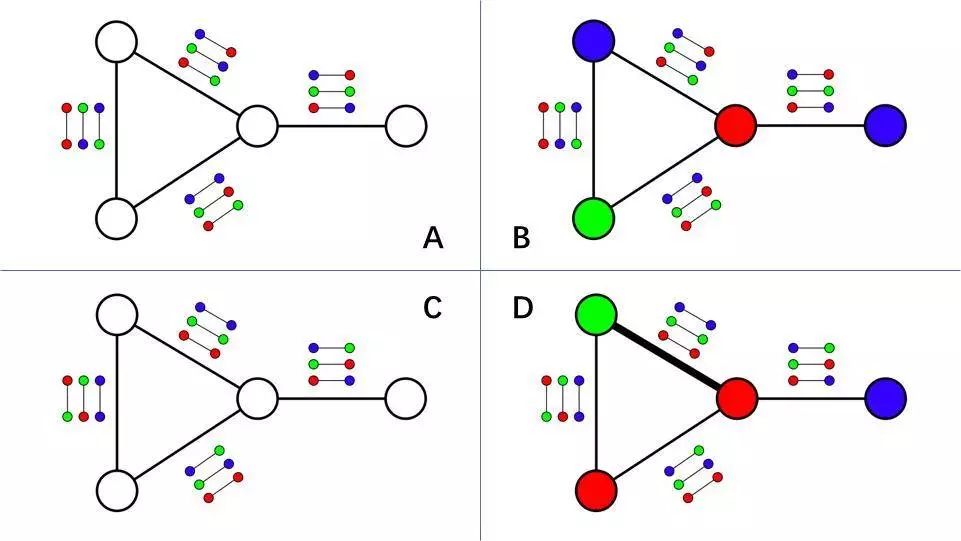
对于 A 中给出的约束规则，可以找到一个满足所有规则的着色方案，如 B。

但有时只能找到满足部分约束规则的着色方案。比如对于 C 中给出的约束规则，可以找到着色方案 D，满足了加粗连边以外三条边的约束规则（满足75%的规则）。

图片来源：Wikipedia

乍看之下，如果图上的着色规则能接近完全满足约束规则，那么找到一种完全满足约束规则的着色方案应该不难。比如某个着色方案在99%的节点上可以符合规则地着色，那么，似乎只要找到能让剩下1%的节点成功着色的方法就可以了。

但 Khot 怀疑，即便已经有99%的节点可以着色，想要找到让剩下1%节点成功着色的方案，也是非常棘手的。根本就没有一种有效的算法，可以为所有的图都找到完全符合规则的着色方案。他猜想，对于一套着色方案算法，即使图上99.9999％的节点都满足着色规则，但要让剩下0.0001％的节点也同时满足，依然是困难的。不论这个比例有多小，都会是困难的。

图片来源：Quanta Magazine

Khot 提出这个猜想的动机与图着色密切相关。但当他和其他理论计算机科学家开始对 UG 猜想做推广时，他们发现它包含的信息远超图着色问题本身。 Khot 说，这个猜想是“自成体系的”。

特别是在 2008 年，加州大学伯克利分校的 Prasad Raghavendra 的工作表明，如果UG猜想是正确的，那么一个叫做半定规划（semidefinite programming）的算法可以为所有的“约束补偿问题”（constraint satisfaction problems，也就是说当你要尽可能满足尽可能多的规则）提供最优的近似解。

伯克利的 Prasad Raghavendra

你可以想当然地将算法设计看作一个有创造性的过程，在这个过程中，你必须找到新颖的算法去解决遇到的每个问题，”Barak 说道。但是 Raghavendra 的工作意味着，如果 UG 猜想是正确的，那么对于许多问题来说，创造性是多余的——半定规划算法就是一种万能的解决方案。

Irit Dinur：为很多事情找到漂亮的解释，是我们的真爱所在，特别是在科学和数学方面。从这个角度来看，我们真的希望这个猜想是正确的。”

德州大学奥斯汀分校的 Dana Moshkovitz 认为，在 Raghavendra 的结果提出之后，理论计算机科学家对 UG 猜想的信任程度，“完全取决于我们是否相信半定规划能够如此强大，”得克萨斯大学奥斯汀分校的 Dana Moshkovitz 说道。而对于许多理论计算机科学家来说，这似乎是一个可疑的命题。

Dana Moshkovitz

他们的疑虑受到了 UG 问题的两个特点的支持。一方面，Khot 的猜想认为，对某些图而言，即使找到让99％节点满足规则，但还是难以找到同时解决剩下的1％节点的着色方案。不过目前还没有人能够找到这样的具体示例。这与其他数学难题形成鲜明对比。例如，当涉及到整数分解时（一个普遍认为没有高效算法的问题），只需将大素数相乘，就可以很容易地找出残差分解算法的数字。

2010年，Barak 与普林斯顿大学的 Sanjeev Arora 和瑞士苏黎世联邦理工学院的 David Steurer 一起为某些形式的 UG 问题，提出了“次指数”算法（sub exponential algorithm）。

次指数算法，指运算时间比多项式级增长得快，但仍明显小于指数的算法。

David Steurer

计算问题的蛮力方法往往带来运算时间的“指数”级增长，可能是2^n或3^n。例如，如果你想用3种颜色为n个顶点着色，那么就有3^n种可能的着色——对于任何计算机来说，其耗时远远超过了可以接受的范围，即便是对于很小的n也是如此。在一个次指数算法中，其指数小于n——例如它可能是n的平方根，这意味着该算法比蛮力方法快得多。尽管还不够快，不足以称为是真正有效的（计算机科学家以使算法的运行时间在多项式级别为荣，例如n^2或n^3）。

在 UG 问题的次指数算法提出之后，“我想至于人们认为的算法，’得了，我们会加把劲研究，最终找到一个真正高效的算法，’”卡内基梅隆大学的 Ryan O’Donnell 说道。要是这种情况发生，UG 猜想将会被证伪。

理论计算机科学家 Ryan O’Donnell

O’Donnell 回顾了2014年在首尔举行的国际数学家大会上午餐时，关于这个理论的非正式地投票。在那次会议中，Khot 被授予奈望林纳奖（Rolf Nevanlinna Prize）——计算机科学最高荣誉之一——在很大程度上，是由于他的在 UG 猜想上做出的工作。而当 O’ Donnell 问谁认为这个猜想是对的时，只有他和 Khot 举手。

O’ Donnell 说：“我觉得 Khot 因 UG 猜想获奖的过程实在有趣，要知道很多人认为这个猜想是错误的”。

3.问题很难，但是可计算

四篇新论文（其中也依赖普林斯顿大学的 Barak，Steurer 和 Pravesh Kothari 的观察以及 Moshkovitz 的观点）所提出的观点，并不能为 UG 猜想提供的完整证据。不过，它证明了 “2-2 Games” 猜想，这是一种类似的猜想。所谓 “2-2 Games”，是指当你为一个顶点着色时，你可以从两种颜色中选择，为它的相邻顶点着色。

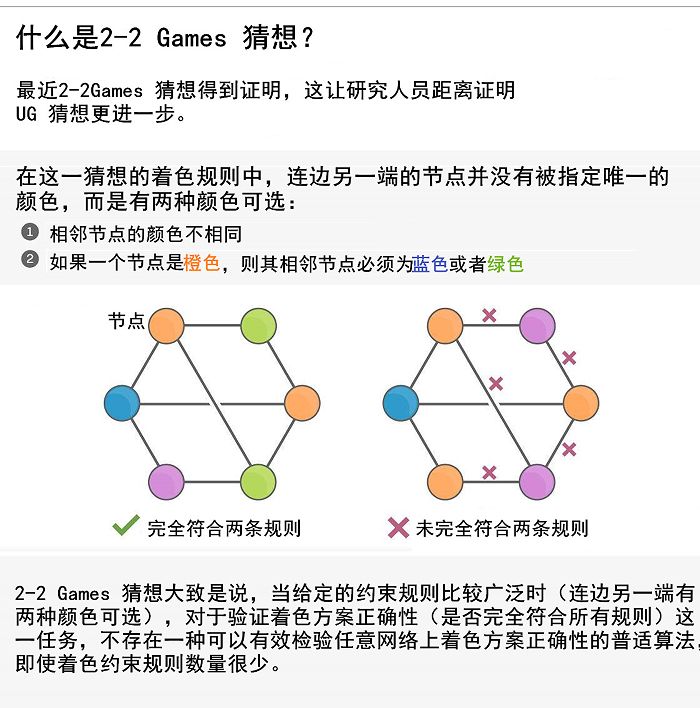
图片来源：Quanta Magazine

但是，这一进展已经足以改变 Barak 关于 UG 猜想的想法。 “我不明白为什么，这些猜想中的某一个是正确的，而其他的则是错误的，”他说道。

具体而言，Khot 对“2-2”问题的新证明为研究人员提供了证明 UG 猜想的途径。有一种简单的方法可以将“2-2”图变成 UG 图——丢弃每个规则两种颜色中的一个。然后，如果你的着色能符合2-2的几乎全部规则，则相同的着色可能会满足你设计的 UG 约50％的规则。

由于这种关联，扩展新的“2-2”证明并不困难。扩展新的“2-2”证明以表明在 UG 的设定中，如果你考虑所有可以满足其至少49％着色规则的方式着色的图（或49.9999，或者低于50％的任何数字），则没有有效的算法，能总是找到满足规则1％或0.0001％或任何其他小数目的着色。换句话说， UG 猜想已经被证明可以满足近50％的规则，但尚未满足几乎全部规则的图。

看到这项最新工作之后，O’Donnell 认为趋势正在转变，但他认为像 UG 猜想这样的问题还是很难解决的。

像 UG 猜想这样的难题，现在用次指数算法就能处理。在一些研究者看来，Khot 等人的工作最令人吃惊的一点是，他们找到了解决难题的可行方法。计算机科学中的几乎所有问题都可以归为两类：要么可以靠一种高效的算法快速解决，要么得用蛮力、占用大量计算资源的算法才能处理。而 Khot 等人的工作表明，UG 猜想这类难题，介于这两者之间。因为众所周知的原因，一些研究者认为这样的问题才是本质的。 “UG 猜想显然位于这者之间的模糊地带，”O’Donnell 说。

Irit Dinur，就职于以色列魏茨曼研究所，正致力于解决 UG猜想。

也许，最令 Khot 兴奋的是，2-2 Games 猜想的证明，已经足以解决他研究生时曾着迷的原始问题的一个弱化版本，关于增加颜色选择后是否可以有效地对图形进行着色。（答案基本上是否定的。）“我认为我在读博士期间的梦想实现了”，Khot 说。

新论文中的许多重要思想都来自团队中的研究生 Dor Minzer，他很有远见卓识。 Khot 说：“Dor 这个家伙很厉害，他才是整个工作的设计师。”

许多研究生可能对解决像 UG 猜想这样著名而棘手的问题感到恐惧，但对于 Minzer 而言，这并不是一种顾虑。 “我的想法是，我有机会与我尊重的两个人一起，思考一个有趣的问题，并且去看看会发生什么，”他说道。

1月份的那一篇构成了 2-2 Games 猜想核心论证的论文，还没有经过理论计算机科学界的彻底审阅。但是像 Barak 和 Dinur 这样的研究人员则确信其大方向是正确的。 Barak 说，论证中最具突破性的想法，在一篇更早的、他曾仔细检验过论文中出现过。

最近的论文“是一个极具参考价值的技术，但我的感觉是，最终它证明了一个非常可信的猜想，即使用这些工具……熟悉这个领域的作者会自然而然地这样做的，” 他在一封电子邮件中写道。 “我认为结论非常坚实。”

研究人员认为，新论文中最大的创新点是找到 Unique Games 问题与“Grassmann 图”（即编码高维空间之间交点的数学对象)之间的联系，但这可能仍不足以解决完整的 UG 猜想。 “但我认为这会让人们更加乐观地认为，我们可能会发现一条解决的路径——UG 猜想的证明或证伪并不是那么难以实现，”O’Donnell 说。