本文由集智翻译组整理自https://thegradient.pub

1.图数据中蕴藏着秘密

事物之间的关联信息，人类已经积累了很多，但绝大多数人不知道如何利用它们。

社交媒体中的互动和关系网络图中，蕴含着深意。像WordNet这样的同义图表能够通过计算机视觉，帮助我们更好地理解和识别特定情形下研究对象之间的联系。从家谱到分子结构，我们周围世界中海量的信息都以图的形式呈现。

尽管普遍存在，图结构（Graph Structure）在机器学习的应用方面还是经常被忽视。比如“时尚潮流推荐问题”，其目标在于发现特定的能够形成凝聚趋势的一些衣服形式，也就是“风格”（style）。通常的做法是从社交媒体抓取图片并识别这些图片中的衣服，然后用这些图片的流行程度代表特定“风格”服装的流行程度。用这种方式去了解流行样式风格当然可行，这个模型能够轻易地通过图数据获得优化。比如，我们可以分析用户社交网络中潮流趋势，或者提取马逊购物网站中的“相关联产品”的集合目录。

那么，为什么结构化的信息经常被忽视呢？因为多数情况下，从这些图表中提取有效的特征实在是个巨大的挑战。

在本文中，我们将探索一些从图数据中提取有效特征的新技术。特别地，我们将重点讨论那些利用随机遍历方法，来量化图中节点之间的相似性。这些技术主要依靠自然语言处理群体的现有结果。我将建议一些未来的研究途径，特别是与时变图形的学习特征有关。最后，我们将简要讨论图卷积网络 (GCNs) 的大家族，它提供了一个在图结构数据上进行机器学习的端到端的解决方案，而无需单独的中间特征提取步骤。

这些方法本身就构成了机器学习的一个子领域，但是研究人员和从业者可以从他们感兴趣的特定范畴的结构中获益。

2.基于图的特征学习

2.1 图摘要的计算

当我们在图上进行机器学习的时候，我们通常需要计算一个图摘要（graph summary），它会将图中每一个顶点映射为一个实值特征向量，而该向量则编码了这个顶点的相邻顶点的信息，这样做对于基于图的机器学习是很有帮助的。如果两个顶点具有相似的邻居(neighborhoods)（这里的“邻居”一词很宽泛，它通常用于捕捉某种局部概念，例如从某一顶点出发，经过1或2跳(hops)的顶点集合都可称为该顶点的“邻居”），我们要学习一个函数，将这两个顶点映射到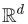空间中的两个相似的特征向量。

然后图中的的每一个顶点的特征向量就可以堆积为一个隐含的特征矩阵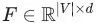。有了顶点的向量化表征之后，我们就可以在其上运行标准的机器学习算法了。这是不是很棒啊！

DeepWalk(2014) 和 node2vec(2016) 正是学习上述特征向量的两个算法。下面我们就一起来看一下这两个算法是怎么工作的吧。

2.2 DeepWalk：将随机游走看做句子？

DeepWalk算法[1]背后关键的思想是，图中的随机游走(random walks)和句子很像。经验发现，句子中的单词和一个真实世界中图上的随机游走均服从幂律分布(power-law distribution)。也就是说，我们可以把这些随机游走路径想象成某种“语言”中的“句子”。

受这种相似性的启发，DeepWalk使用原本被用于自然语言建模的优化技术来构建图摘要。在标准的语言模型中，我们通常是给定某个词的周边词，然后来估计该词出现在一个句子中的概率。另一方面，在DeepWalk算法中，则是给定某个顶点之前的顶点集合，来去估计该顶点出现在一个随机游走过程中的概率。并且和语言模型一样，我们还试图去学习顶点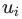的特征向量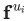，以便估计这个概率。具体来说就是，给定某个分类器，去估计概率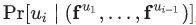。我们的目的是，从向量空间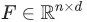中，选择特征向量，最大化如下目标：

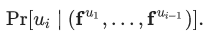
然而遗憾的是，随着随机游走路径长度的不断增加，这个目标是很难处理的。因此DeepWalk论文作者使用给定当前顶点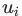的向量表征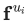，来去预测其附近2w距离的邻居顶点（注：w为窗口大小），从而重新界定了该问题。（从技术上来讲，这是一个不同的优化问题，但是它可以作为之前目标的一个合理且与顺序无关的替代目标[2]）换句话说，我们要最大化目标概率：

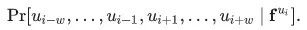
但是，我们如何在整个随机游走空间上最小化（译者：最小化？不是最大化吗？）该目标呢？其中一个策略如下（请注意, 论文作者另外假设了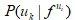的条件独立性）：

抽样一个顶点v，并生成一个随机游走序列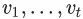，其中。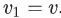

对该序列中每一个顶点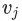和每一个小于某一步长的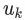，在向量空间 F 上，应用梯度下降算法，最小化损失函数。

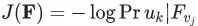这个算法虽然可行，但是也使得最后应用梯度下降算法的步骤变得尤为复杂，使得至少要更新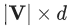个参数。这对于数百万级规模的图来说，是一个非常严重的问题。

为了解决这个问题，DeepWalk的作者使用“分层softmax (hierarchical softmax)”的方法（很抱歉，该方法不在本文介绍范围内），将该优化问题拆解为一个二分类器的平衡树(balanced tree of binary classifiers)。使用这些二分类器，可以将最后一步梯度下降算法的参数更新个数，从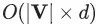减少到。

Deepwalk算法示意图

2.3 Node2vec：泛化到不同类型的邻域

Grover and Leskovec (2016)[3] 将Deepwalk算法拓展成为node2vec算法。与deepwalk算法不一样，我们不再根据现有的结点运用一阶随机游走（first-order random walks）选择下一个节点，node2vec不仅基于现有结点，还会使用现有结点前面的那一个结点，从而使用一系列二阶随机游走。

我们可以在随机游走的每一步通过调节两个参数值来确定具体的分布：大概来说，我们可以通过降低p值从而让随机游走偏向“探索”模式；同时，我们也可以通过提高q值让随机游走实现“广度优先”(breadth-first)模式。

这篇论文的关键想法是通过选择不同模式的二阶随机游走，我们可以提取到网络图的不同特性。

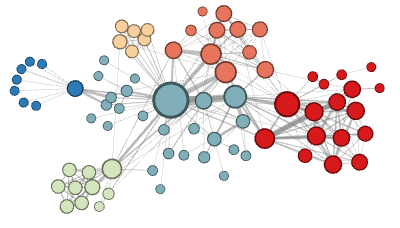
为了证明它的必要性，作者们在文中给出了两种在网络图上做机器学习通常使用的邻域类型：（节点颜色代表类别 ）

在同质性假设下，由于高度连接的节点在网络图里位置相近，因此它们属于同一个邻域。

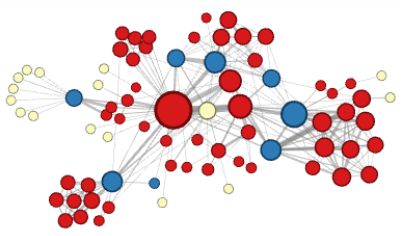
在结构性假设下，承担着相似结构性功能的节点（比如说，网络的所有中心节点）由于他们高阶结构性显著度，它们属于同一个邻域。

用两个参数, 作者们提供了一种非常好用的方法在这两种邻域类型之间相互转换。

就像Deepwalk一样，node2vec的目标函数可以通过抽样来实现最优化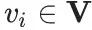，采用（p,q）随机游走，然后通过梯度下降（gradient descent）来更新F，达到优化的目的。

2.4 时变网络（temporal networks）中的潜在特征

这些图摘要技术很有用，但现实世界中很多图是随着时间变化的时变网络。比如，社交网络中一个人的朋友圈图会随着时间发生扩张或者收缩。我们可以使用node2vec，但是有两个缺点：

每次随着图的改变而运行一个新的node2vec实例很耗算力
其次，难以保证多个node2vec的实例能产生相似的甚至是可比较的Ｆ矩阵

对于第一个问题，有一个解决方法–每次网络改变后不立即运行node2vec，而是直到足够多的边发生改变使得原始嵌入的特征矩阵Ｆ质量下降再运行。

那么多少条边发生改变才可以被认为发生了“显著”的变化呢？这高度依赖于图中特殊的边和随机游走中的(p, q)两个参数。

观察下面这些图：

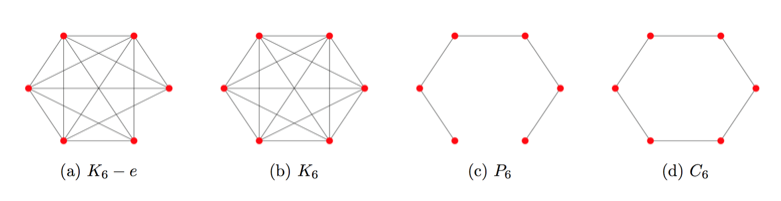
注意到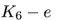的领域和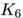的邻域很相似。然而，一条额外的边把路径图转换成闭环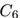，显著地改变了图的随机游走邻域。类似这样，连接网络中的无连接或弱连接部分，起到桥梁作用的边，相比其它边更可能对邻居产生显著影响。

幸运的是，很多现实世界中的图，比如社交网络，更倾向于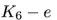这种类型。网络是高度连接的，增加和删除节点的某条边不会对DeepWalk中使用的一阶随机游走的嵌入产生显著影响。需要注意的是，一阶和二阶的随机游走差别很大，因此这里的讨论内容对于扩展到node2vec可能并不是必要的。

在某种程度上，第二个问题可以通过连接从多个node2vec实例得出的特征，然后训练一个自动编码器，把这些综合特征映射成压缩的表示。

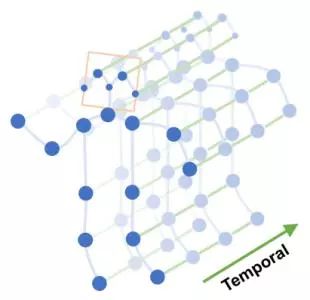
如何实现时变网络上的可扩展特征学习呢？对于时变网络，一些工具可以用于图嵌入的增量更新，比如Abraham et al.(2016)[4]提出的动态频谱稀释器。这方面仍然有大量工作需要做，即使是最好的稀释器也因为速度太慢而难以实际应用于现实世界中的图，即使存在亚对数算法，算法的常量因子也非常大。我相信，结合动态图分割技术和更新图摘要矩阵Ｆ对于时变图的特征摘要来说或许是一个可行的方法。

另一个可选的方法是泛化node2vec算法到时变网络，通过添加一个额外的参数λ，影响随机游走经过“时变边界”的概率。有些预测任务中可能有“时变位置”的概念，其中有着相似时间戳的图的快照是相关的，而其他的或许有更久的依赖关系。

接下来我们开始介绍图卷积网络，一种最近提出的网络图上机器学习的方法。

3.图卷积

Node2vec和DeepWalk的方法都是先生成“语料”然后用于后续的机器学习技术。相比之下，图卷积（GCN）则是展示了一种端到端的方法进行结构化学习。

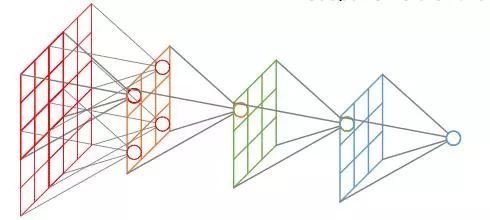
图卷积

GCN尝试将传统的卷积神经网络推广到可变的、无序的结构中。由于图没有明确定义的顺序，因此节点的排序不应该对GCN产生影响。很显然，CNN并没有这个特性，因为随机交换图像像素矩阵的行和列，再输入给CNN必然会改变计算的输出（通常，用于视觉问题的CNN，在识别图像中的边缘或其他局部结构时，其输入在不同的行列置换下，计算结果并不是一成不变的）。

此外，CNN对像素邻域的形状并不是不可知的，换句话说，并没有明显的方式可以训练一个CNN同时接受在正方形和六边形网格上定义的图像，即一个内在像素分别具有八个和六个直接邻居。因此，为了解释一般图的动态结构，必须对CNN的激活函数（activation function）进行合理的松弛（relaxations）。

很多作者提出了不同的GCN松弛（relaxations）方法。其中一篇文章[5]定义了一种和CNN类似的方法，该方法优化了稀疏过滤器，而过滤器在多个尺度上对图进行聚类操作。这篇文章还提出了CNN的谱近似方法，CNN中多个谱过滤器作用在对应最大特征值的特征向量上。另外一篇文章[6]提出了一种和CNN更新具有相同的时间复杂度的GCN更新方案，即对谱过滤器只进行低度的多项式近似。还有一篇文章[7]通过使用多个线性谱过滤器简化了GCN的公式，这些过滤器可以共同捕捉高阶特征。

这些图卷积网络公式本身就很有趣，需要更多篇幅来详细描述。GCN作为之前章节描述的图处理方法的合理替代方案已经显示出了前景。GCN的完全可微分的特征也使得其稀疏过滤器能够成为端到端学习算法的一部分。虽然node2vec的偏置超参数(p, q)允许发现更多个性化的特征，但是GCN的权重矩阵也可以根据提供的训练数据进行调整。

结构化学习已经被应用到生物化学领域，文章[8]提供了一种端到端的和全微分的神经网络来预测基于稀疏原子结构的蛋白质-配体亲和力。另一篇论文[9]用GCN解决了药物发现问题，并引入了一个虚拟的“超级节点”，该虚拟的“超级节点”通过有向边连接到候选药物图中的每个节点，以便得到图特征。

GCN也已经成功应用在知识图[10]的链接预测和实体分类等方面。最近出现的结构化学习的成功和快速的研究在未来几年还会有更多。也许我们很快就会看到利用关系结构如知识图的GCN网络来提高计算机视觉中物体检测的性能，也或许，通过结构化学习方法能够加速蛋白质折叠模拟，从而大大降低原子度低的三维蛋白质的维度等等。这些应用几乎可以肯定将会出现（如果尚未发布的话），这当然使得结构化学习成为一个令人兴奋的领域。

4.参考文献

[1]Rami Al-Rfou “DeepWalk: Online Learning of Social Representations[J] knowledge discovery and data mining, 2014: 701-710.“

https://arxiv.org/abs/1403.6652

[2]Tomas Mikolov “Efficient Estimation of Word Representations in Vector Space[J] arXiv: Computation and Language, 2013.“

https://arxiv.org/abs/1301.3781

[3]Aditya Grover，Jure Leskovec “node2vec: Scalable Feature Learning for Networks [J] knowledge discovery and data mining, 2016: 855-864.“

https://cs.stanford.edu/people/jure/pubs/node2vec-kdd16.pdf

[4]Abraham et al.”On Fully Dynamic Graph Sparsifiers.[F] New Jersey, USA, 2016, pp. 335-344.“

https://ieeexplore.ieee.org/abstract/document/7782947/

[5]Bruna, Joan, et al. “Spectral networks and locally connected networks on graphs. arXiv:1312.6203“

https://arxiv.org/abs/1312.6203

[6]Defferrard, Michaël, Xavier Bresson, and Pierre Vandergheynst. “Convolutional neural networks on graphs with fast localized spectral filtering. arXiv:1606.09375 [cs.LG]”

https://arxiv.org/abs/1606.09375

[7]Kipf, Thomas N., and Max Welling. “Semi-supervised classification with graph convolutional networks. arXiv:1609.02907 [cs.LG]”

https://arxiv.org/abs/1609.02907

[8]Gomes, Joseph, et al. “Atomic convolutional networks for predicting protein-ligand binding affinity. arXiv:1703.10603 [cs.LG]”

https://arxiv.org/abs/1703.10603

[9]Li, Junying, Deng Cai, and Xiaofei He. “Learning Graph-Level Representation for Drug Discovery. arXiv:1709.03741 [cs.LG]”

https://arxiv.org/abs/1709.03741

[10]Schlichtkrull, Michael, et al. “Modeling Relational Data with Graph Convolutional Networks. arXiv:1703.06103 [stat.ML]”

https://arxiv.org/abs/1703.06103