网络遇见大数据：在大型静态数据集中恢复动态网络

导语

我们正身处于大数据时代，从基础物理学到生命以及社会科学，几乎所有学科都孕育出了体量巨大的数据集，数以千计的变量纠缠其中，隐藏着许多我们未曾发现的关系与自然法则。近日发表在 Physics Reports 的综述文章，介绍了一个从大型静态数据集中恢复动态网络的统一框架，为挖掘大数据中蕴含的深层次信息提供了一种新思路。
陈昊 | 作者邓一雪 | 编辑

论文题目：
Recovering dynamic networks in big static datasets
论文地址：https://doi.org/10.1016/j.physrep.2021.01.003

伴随着各类传感器的使用与数据存储能力的提升，大型数据集在各个领域变得越来越普遍。为了挖掘复杂的数据中蕴含的信息，多种多样的信息处理手段层出不穷，网络理论与方法则在其中扮演了重要的角色。然而，受到技术、道德等多方因素的限制，我们获取到的数据通常是静态的，基于静态数据重构出的网络无法揭示出足够的信息。为了解决该问题，最近发表在 Physics Reports 的一篇文章提出了一种从大型静态数据中恢复动态网络的统一框架。该框架结合了异速生长率与进化博弈论，使用常微分方程组对静态数据样本进行建模，引入生态位的概念来弥补静态数据缺少时间维度的不足。除此之外，本文针对常微分方程组模型下的网络社区划分、多空间网络构建、超网络构建等问题进行了详细的描述，给出了由静态数据到动态网络的完整解决方案。

1. 网络遇见大数据

在过去的三十多年中，网络理论与方法得到了充分的发展。与其他方法一样，网络工具的应用也依赖于网络推断的数据类型。从广义上讲，用于网络重构的数据包括静态和动态两种类型。相对而言，静态数据更加容易收集，因此更常用于分解复杂的系统。但是从静态数据重构出的网络有几个主要限制。首先，真实的复杂系统中进行的交互并不是静态的，而是在时间和空间维度上展开。因此，针对不同时间、空间等状态重构特异性网络对于了解变量间的关系十分重要。然而，使用静态数据的方法通常只能通过全部样本表征整个网络，无法识别出样本间的异质性。其次，具有详细交互信息的网络才能应用于实际问题。信息完全网络定义为由双向有符号加权（bidirectional, signed, and weighted，bDSW）连边编码的网络。然而由静态数据重构的网络大多不包含这些信息，在实际中用途有限。例如基于相关性的方法只能评估变量交互的强度，而无法确定变量间的因果关系；通过贝叶斯方法进行建模可以重构有向无环网络从而揭示因果关系，但却不能对因果关系的符号（促进或抑制）进行编码。尽管目前已经做出了巨大的努力来改进基于相关性和贝叶斯方法重构的网络，但是由静态数据带来的主要缺点仍然无法克服。通过增加时间和扰动成分，动态数据具有更多的网络重构信息。将动态数据整合到布尔网络和贝叶斯网络中，可以重构出有权、且因果关系明确的网络，其中动态贝叶斯网络（dynamic Bayesian networks，DBNs）已经成为多种学科中网络重构的主流方法，然而这种方法会受到数据时空尺度的影响。通过使用常微分方程组（ODEs）对变量进行建模可以解决该问题，从而重构出信息完全的网络。常微分方程组方法的另外一个优点是它可以被表示为时间的函数，从而提供了一种预测动态网络结构的方法。常微分方程组方法对数据的时间密度有着很高的要求，然而在诸如医学的许多领域中，受到技术、道德等条件的约束，动态数据通常是难以获取的。为了解决二者的矛盾，从静态数据集中提取动态信息的方法正在被发展。这些方法的出现有助于将强大的网络工具广泛应用于各种科学、技术与管理领域。

2. 将静态数据转换为动态表示的统一框架

任何类型的对象，其功能和行为始终由其组成部分之间以及与周围环境的相互作用来决定。这使我们可以将网络视为由所有生物（生物物种）和非生物因子（包括温度、营养素、水和氧气的非生物环境元素）相互作用组成的生态系统。这些因素之间的相互关系不仅影响单个物种的生存和生长，而且还决定了生态系统的整体功能。对于特定物种至关重要的生物和非生物因子被称为该物种在生态系统中的生态位（ecological niche）[1-2]，不同物种的生态位被共享的程度取决于这些物种如何竞争或合作以争夺生态系统中的资源。通过对单个物种的生态位与生态系统总生态位之间的关系进行建模，生态学家可以研究每种物种如何以及在多大程度上对整个生态系统做出贡献。类似地，对于要重构的网络，我们可以将变量的观测值看作其“生态位”，它反映了该变量对整个系统的作用。与之对应，也可以将所有变量的总观测值看作网络的“总生态位”。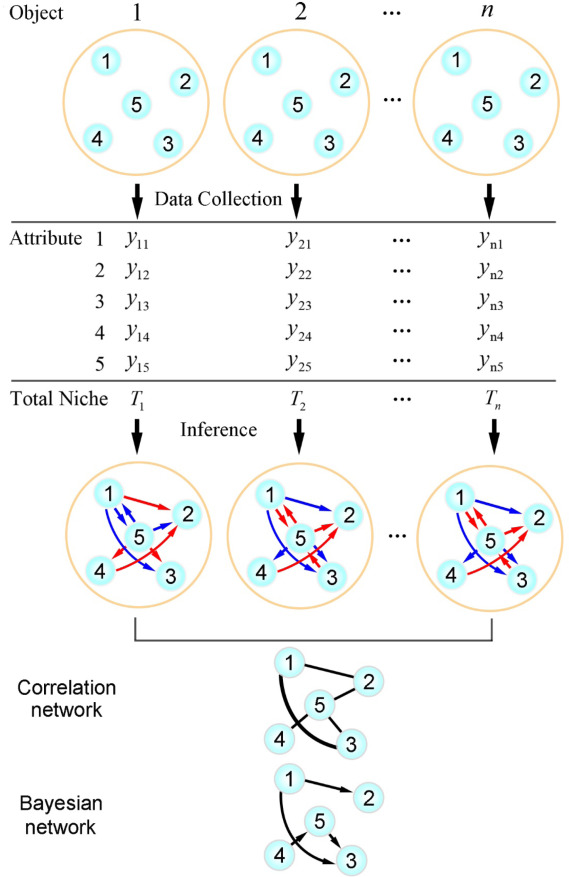
图1 从研究对象收集数据的采样策略对象i(i=1,…,n)是对复杂系统的n次采样，由m=5个属性进行描述。

假设在一个实验中有n个采样对象，每个对象被可以被看作由m=5个变量来描述的系统。由于变量只能在单个时间点测量，因此采样得到的数据是静态的。yij 表示样本i(i=1,…,n)的变量j(j=1,…,m)的观测值，如图1所示。Ti表示所有变量的总观测值，表示为

通过对这些静态数据进行适当的建模和推断，我们可以重构针对特定样本的信息完全网络。值得注意的是，基于相关性的方法只能重构出有权重但无因果、无符号的网络，贝叶斯方法则只能重构出有因果但无权重、无符号的网络。系统中的单个生态位与总生态位之间满足异速生长率。例如对于三维对象，其长度与体积成三分之一次幂。在生物学中，该定律被概念化为一种分配过程。通过该过程，生物体将定量的资源分配给不同组成部分，以更好的适应环境变化。该定律可以以数学形式表示为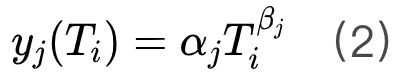

通过估计参数 (αj, βj)，我们可以表征不同变量如何在样本中进行改变。进化博弈论（参见原文2.3）可以帮助我们将动态演化的系统表示为一系列常微分方程。虽然图1表示的系统不具备时间维度，但我们可以通过异速生长率来将变量表示为总生态位的函数，从而得到一个qdODEs（quasi-dynamic ODEs）系统，在该系统中时间导数被总生态位导数代替。针对m个变量的qdODEs可以表示为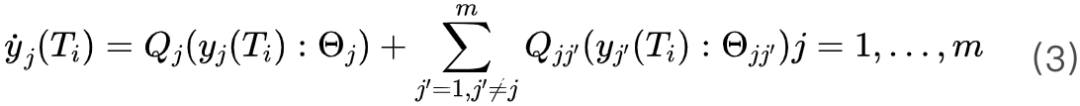

上式将变量j对总生态位导数的观测值表示为两部分：独立部分 (简化表示为Wj(Ti))与相互作用部分 (简化表示为Wjj'(Ti))。qdODEs的推导以生态系统理论的视角整合了异速生长律与进化博弈论，为从静态数据重建信息完全网络提供了基础。

3. 静态网络的统计推断

为了描述一个复杂系统，我们当然需要尽可能地确定变量之间的因果关系，但这并不意味着我们需要估计和测试每对变量之间的所有关系。在现实世界，尤其是生物学中，很少存在全连接的网络。为了增强网络的鲁棒性，网络通常是稀疏的[3]。此外，真实网络还会通过随机波动来提高网络稳定性[4]，并使资源消耗最小化[5]。总而言之，确保网络稀疏性、因果关系和稳定性是网络重构的重点[6]-[8]。以因果关系为例，变量j’对变量j的影响可以由方程（3）中对Wjj'(Ti)的极大似然估计表示。Wjj'(Ti)为正、零以及零负分别表示变量j’对j有正面、负面以及没有影响。如表1所示，结合Wjj'(Ti)与Wj’j(Ti)便可以对两个变量的相互因果关系进行具体的分析。特别的是，当Wjj'(Ti)与Wj’j(Ti)均为0时，两个变量之间没有连边。综上，通过qdODEs重构的网络天生具有量化的因果关系。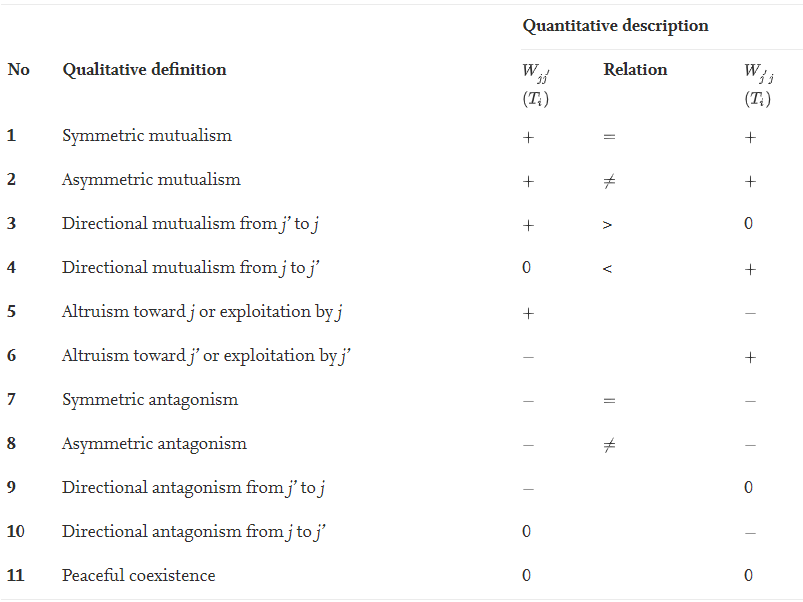
表1 两个变量之间相互作用的完整定性、定量描述
为研究基因与常见疾病的因果关系，正在进行的GTEx项目收集了近1000位实验志愿者上万个基因的组织特异性表达值[9]。本篇综述使用GTEx项目中的真实数据重构了稀疏、因果明确、稳定的网络（图2）以说明qdODEs方法的有效性。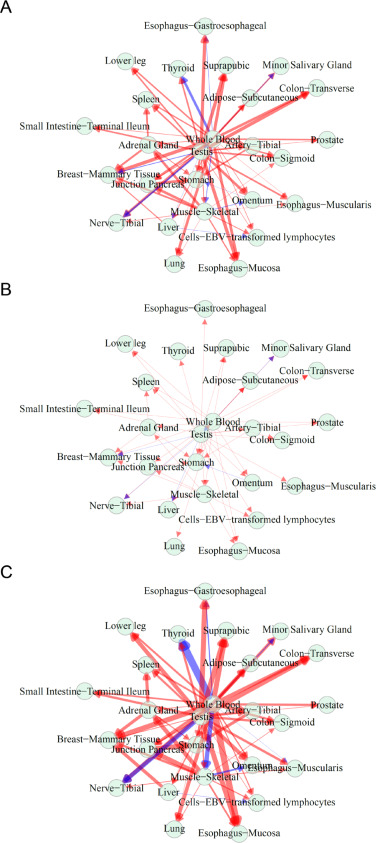
图2 GTEX-11EQ9中基因驱动的组织通信网络。图A为完整网络，由56200个基因驱动。图B为由DAZ1（总生态位最小的基因）驱动的网络。图C由MT-CO2驱动的网络。红色和蓝色分别代表促进和抑制，线的粗细与促进或抑制的强度成比例。

4. 跟踪网络的动态变化

从生物领域到社会领域的复杂系统都会进行动态变化，从而优化其结构与功能[10]。目前许多网络重构的方法都只能得到节点固定的静态网络，这种网络无法被用来研究时空变化的复杂系统。近年来，动态网络分析越来越受到人们的关注[11]，几项计算医学研究已经开始考虑针对特定基因的网络推理[12][13]，这对于了解复杂系统适应或响应外部干预的机制有很大的帮助。然而，现有的方法[12][14]无法很好地捕获变量间的因果关系，qdODEs方法则克服了这种局限性。以Davenport等人[15]得到的人类粪便微生物组丰度数据为例，该数据来源于127位健康个体，93位在冬天测量、91位在夏天测量，其中57位在冬夏都进行了测量，总计184份样本。针对每一份样本使用qdODEs重构种群层面的微生物相互作用网络，图3为其中具有代表性的三个网络。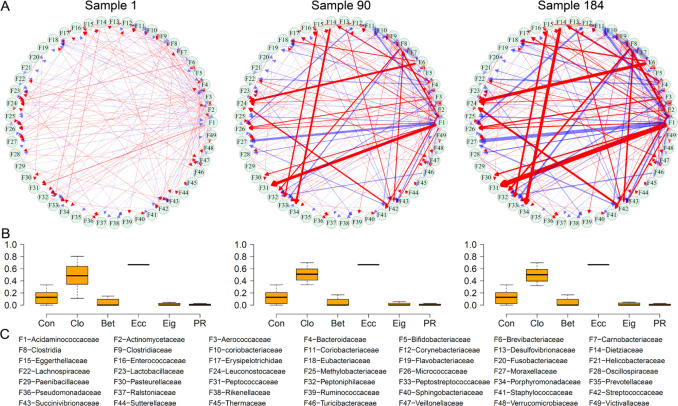
图3 基于特定样本的微生物相互作用网络图A中的三个网络分别表示总生态位最小（Sample 1）、居中（Sample 90）、最大（Sample184）。图B为每个网络的六个网络参数：connectivity (Con), closeness (Clo), betweenness (Bet), eccentricity (Ecc), eigenvector (Eig) 和PageRank (PR)。图C为 49个微生物种群的名称。

在不同的状态（如时间、位置、干预措施）下，网络结构可能会有不同的表现，因此将针对样本的网络转换为针对特定状态的网络是十分有必要的。为此我们需要分析不同状态下的样本的差异性。假设共有C种状态，每种状态包含nc种样本，针对每一种状态有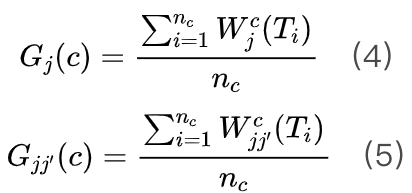

其中Wj(Ti)和Wjj'(Ti)分别为变量j的独立和非独立成分。将Gj(c)编码为节点、Gjj'(c)编码为连边即可得到特定状态下的网络。图4展示了不同季节、性别与年龄阶段下得到的微生物相互作用网络。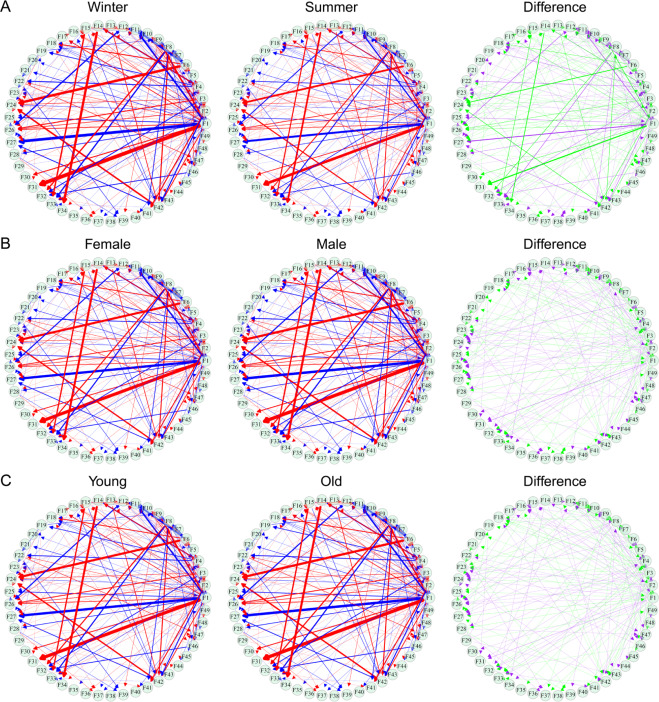
图4 将针对特定样本的网络转化为针对特定季节（图A)、特定性别（图B）、特定年龄（图C）的网络

5. 总结

除上述内容外，该综述还涉及了对多空间网络、超网络等情形的讨论与技术介绍。现代科学正以惊人的速度发展，先进的仪器和技术让我们获得了各类十分庞大、完整的数据。传统的统计和计算方法难以揭示出高维数据间的因果关系，而网络则提供了一种前所未有的方式来表示、重构、研究数据间的复杂关联。为解决现有网络方法难以处理静态数据的问题，这篇综述结合异速生长率与进化博弈论，建立了一个由静态数据推断出多种有意义的动态网络的统一框架，证明了qdODEs方法的优越性，对挖掘物理、生物等多个学科中的深层次规律可以起到巨大的帮助。
参考文献

[1] Townsend Peterson A, Soberón J, Pearson R G, et al. Ecological niches and geographic distributions[J]. Princeton UP, Princeton, 2011.
[2] Pereira F C, Berry D. Microbial nutrient niches in the gut[J]. Environmental microbiology, 2017, 19(4): 1366-1378.
[3] Busiello D M, Suweis S, Hidalgo J, et al. Explorability and the origin of network sparsity in living systems[J]. Scientific reports, 2017, 7(1): 1-8.
[4] Runge J. Causal network reconstruction from time series: From theoretical assumptions to practical estimation[J]. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2018, 28(7): 075310.
[5] Dunbar R I M. Neocortex size as a constraint on group size in primates[J]. Journal of human evolution, 1992, 22(6): 469-493.
[6] Michailidis G, d’Alché-Buc F. Autoregressive models for gene regulatory network inference: Sparsity, stability and causality issues[J]. Mathematical biosciences, 2013, 246(2): 326-334.
[7] Zavlanos M M, Julius A A, Boyd S P, et al. Inferring stable genetic networks from steady-state data[J]. Automatica, 2011, 47(6): 1113-1122.
[8] Larvie J E, Sefidmazgi M G, Homaifar A, et al. Stable gene regulatory network modeling from steady-state data[J]. Bioengineering, 2016, 3(2): 12.
[9] GTEx Consortium. The Genotype-Tissue Expression (GTEx) pilot analysis: Multitissue gene regulation in humans[J]. Science, 2015, 348(6235): 648-660.[10] Sreedharan J K, Magner A, Grama A, et al. Inferring temporal information from a snapshot of a dynamic network[J]. Scientific reports, 2019, 9(1): 1-10.
[11] Muldoon S F, Pasqualetti F, Gu S, et al. Stimulation-based control of dynamic brain networks[J]. PLoS computational biology, 2016, 12(9): e1005076.
[12] Kuijjer M L, Tung M G, Yuan G C, et al. Estimating sample-specific regulatory networks[J]. Iscience, 2019, 14: 226-240.
[13] Liu C, Zhao J, Lu W, et al. Individualized genetic network analysis reveals new therapeutic vulnerabilities in 6,700 cancer genomes[J]. PLoS computational biology, 2020, 16(2): e1007701.
[14] Wang Y, Cho D Y, Lee H, et al. Reprogramming of regulatory network using expression uncovers sex-specific gene regulation in Drosophila[J]. Nature communications, 2018, 9(1): 1-10.
[15] Davenport B, Li Y, Heizer J W, et al. Signature channels of excitability no more: L-type channels in immune cells[J]. Frontiers in immunology, 2015, 6: 375.

参考文献可上下滑动查看

网络科学新课推荐：网络动力学

集智学园特邀陈关荣、项林英、樊瑛、宣琦、李翔、史定华、李聪、荣智海、周进、王琳等网络科学专家作为导师，依托汪小帆、李翔、陈关荣的经典教材《网络科学导论》，自2月27日起开展系列上线课程，以网络动力学为主线构建网络科学知识体系。欢迎希望进入网络科学领域、提高网络分析能力、与一线专家探讨问题的朋友报名参加！

点击查看课程详情：2021重磅新课：探索网络动力学——网络科学第二期