导语


著名物理学家海森堡曾经说过：“提出正确的问题，往往等于解决了问题的大半。”当我们讨论复杂系统时，最核心的问题是什么？生命起源和意识起源是什么？为什么如湍流、台风之类的复杂系统会逐渐瓦解，而如生物体特别是生态系统这样的复杂系统却能长久存在甚至实现不断的进化？从非生命到生命，究竟跨越了怎样的关键一步？复杂系统的层次跨越发生了什么，不同尺度之间的联系如何研究？伟大数学家冯·诺依曼的生命之问，又该如何回答？


由北京师范大学教授、集智俱乐部创始人张江等发起的「因果涌现」系列读书会已于8月14日启动，共读硬核文献，梳理因果涌现理论、机器学习重整化技术、自指动力学等近年来新兴的理论与工具。读书会将持续7-8周，欢迎感兴趣的朋友参与，详情见文末。


因果涌现读书会第一期，张江老师做了《涌现、因果与自指——“因果涌现”理论能否破解生命与意识之谜》分享，带你走进世界最深刻的秘密，看生命如何借助宇宙的漏洞（Bug）来超越热力学第二定律。本文是张江老师分享的内容记录。我们将通过复杂系统的核心问题、冯·诺依曼的生命之问、涌现与因果究竟如何联系引入最核心的概念，然后详细介绍因果涌现的理论框架、粗粒化、整合信息论、机器学习驱动的重整化、以及自指动力学等一系列重要的思想、方法和技术。借助这些帮助，我们将有望破解复杂系统的核心问题，探寻生命与意识之谜。

张江 | 讲者

黄华津 | 整理

梁金 | 编辑



一、什么是复杂系统的核心问题？




我们都知道，许多相互作用的个体可以展现出宏观的模式（pattern），当这一模式被观察到具有其所有组成部分本身没有的属性时，这便是涌现（emergence）。涌现是复杂系统最基本的特质。事实上，相互作用在自然界中实在太过普遍，以至于涌现现象在各个尺度上都会出现，而且随处可见，这便导致了复杂系统无处不在。


诸如大气环流、交通流、鸟群、蚁群等，都是复杂系统


然而，这也导致人们对复杂系统认识的混乱，这不仅指有些时候人们以抽象的、没有根据的、实际上几乎无关紧要的术语谈论复杂性，也是因为复杂系统似乎没有一个核心问题。比如下面是一张网络上找到的图，虽然不是很全面，但我们可以清楚看到几条并行的路线：有的是从复杂性科学到网络科学，有的是从建模的角度，从基于主体的建模（agent based modeling，ABM）到计算建模（computational modeling）等等。


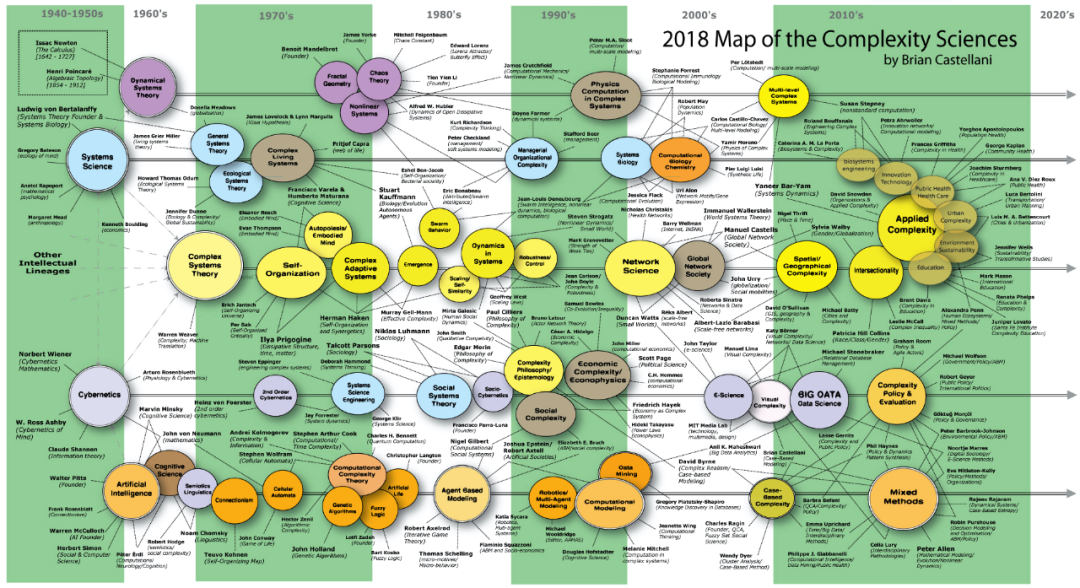
科学家 Brian Castellani 在 2018 年制作了“复杂性科学地图”（请注意，这是多次迭代之一，将来可能会进行更多迭代），当进入网页并单击任何节点的超文本链接时，将会提供有关该概念或人员的详细信息。（https://www.art-sciencefactory.com/complexity-map_feb09.html）


不过，从我个人的理解，复杂性科学确实存在一个核心问题 。事实上，在谈到复杂性时，我们更加关注一个活的、有生命的系统，那么，什么是生命便成为复杂性科学的核心问题。对于这一问题，很多人第一反应或许是，这不是生物学应该研究的内容吗。但从系统科学层面讨论，我们需要的是从具体的生物体提炼出来的抽象模式，也即生命的“软件”。当然，很多知识仍旧需要我们回到生物的物质基础，但我们的核心目的，仍旧是从其中提炼出一组能够泛化到各个生命之中的特性。针对这一问题，我画了一张图，随机选了一些理论放在上面，坐标左边是物理，右边是信息与计算，而生命恰好就在这条轴的中间。这张图告诉我们，生命的奥秘实际上是物理和信息的交汇。


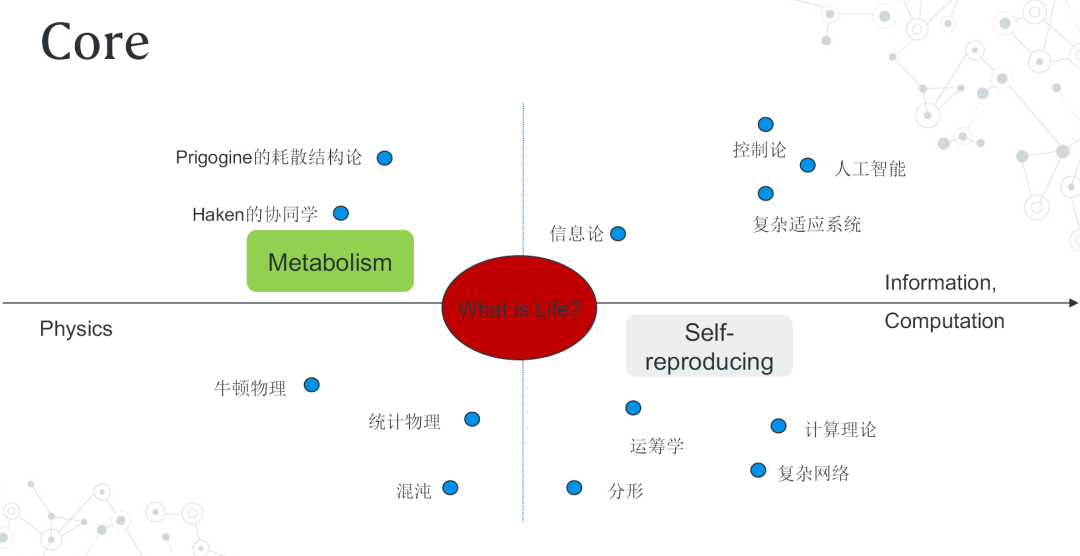
生命处在物理和信息的交汇处


   



二、冯·诺伊曼的生命之问




虽然暂时还没有人能够说清楚生命的真相，但我认为，著名数学家冯·诺依曼对此有独到的见解。在他的著作 “Theory of Self-Reproducing Automata” 中，一系列关于复杂性和生命的重要问题得到讨论。


冯·诺依曼提出，所有已知的复杂系统，存在一个明确的分水岭，分水岭的左边，大部分是人造系统，比如当时的计算机、汽车、厂房等等；分水岭的右边，大部分是诸如人的大脑、细胞、生命、生态系统等大自然形成的系统。在分水岭左边的系统，随着时间的变化会不断降级，比如我们需要经常保养汽车，否则就会出各种问题；与此相反，在分水岭右边的系统，不仅不会随着时间的变化而降级，反倒能够不断进化，特别站在生态系统角度看，其中的物种能生生不息，并且似乎变得越来越高级。由此，冯·诺依曼判断，在复杂系统中存在一个复杂度阈值，如果系统的复杂度没有超过阈值，那么系统便会在热力学第二定律的作用下不断降级，以至于最后瓦解，相反，一旦超过这一阈值，系统便仿佛能够超越热力学第二定律，得以不断升级并进化。对此，冯·诺依曼提出问题，复杂系统的阈值究竟是什么？


复杂度阈值


在我的复杂性思维课程中，我设计了一张图：复杂性阶梯，阶梯的每一步按照复杂系统从简单到复杂的演化过程排列，我用混沌-聚集-网络-自复制-层级跃迁几个阶段将其表示出来，即随着演化过程，系统会从混沌无序走向聚集有序，而为了长期存活，系统便必须开放自己形成新陈代谢和内部网络，更进一步，系统便会升级出像生命一样自我复制的能力（广义上看，便是自指在生命中的表现），最终实现层级跃迁，成为新的个体从而开始下一个复杂性阶梯循环。而攀登复杂性阶梯最关键的一步，便是冯·诺依曼的生命之问，即关键阈值在哪里。对此，我认为这一阈值就在网络和自复制之间，而要想回答这里面究竟发生了什么，就必须回到复杂系统的源头，从最原始、最神奇的一类现象说起。


复杂性阶梯


   



三、涌现与因果如何联系起来？




所有的复杂系统中，最基础的现象便是涌现。不过从下面这张图中，我们却可以看到，涌现不一定只发生在复杂系统中：在风和水汽的作用下，一片巨大的云朵形成，并逐渐产生出一个特殊的形状，仔细一看，其形状仿佛构成了伟大领袖的面容。所谓的涌现，便是在宏观尺度下出现的一种 pattern，正如由云朵、水汽构成的图形，这一图形会至少让我们这些外在的观察者认为，它是一个新型的整体并具有新的特性，而这种特性我们无法从小水滴和水汽尺度上得到，只有当我们将其看成一个整体时才能出现，涌现的精髓便在于此。


偶然的自然气候变化下产生了特殊的形状


更进一步，如果我们追问，涌现是什么，那么可以这样回答，涌现就是一个系统或者说一组东西，当然，这些东西不一定构成了复杂系统。比如下面这张图，图的左边是整体，右边是放大的细节，可以看到，在宏观上出现了一个“无”字，中观上出现的是“整体论”，而微观上，出现的却是“简化论”。这便是涌现的奥秘，它超出了我们往常认为一个系统只能表达一个意思，事实上，正如这张图所示，我们从不同的尺度去观察，完全有可能得到不同的信息。


从不同的尺度观察一个系统，可能得到不同的信息


现在，我们需要暂时放下涌现，进入到另一个关键领域：因果（causality）。我们集智俱乐部近年来举行了一系列因果读书会 ，很多因果科学的研究者都在我们的社群里。在这里面，大家进行了非常专业且深刻的讨论，不过在今天，我只结合涌现来谈一谈二者的相互联系。


让我们首先从 Judea pearl 的因果之梯说起。在因果科学中，有两个最关键的概念，即反事实和干预。通过这两个关键概念，我们得以判断究竟是否存在因果关系，从而破除迷惑大量哲学家和数学家的浓雾。进一步地，我们最新的因果涌现读书会与其存在一个非常有趣的对话点，即在复杂系统里，存在多个层级和多种尺度，这不仅可能表现为不同层级和尺度下存在不同的因果关系，甚至有可能存在跨层级的因果联系。


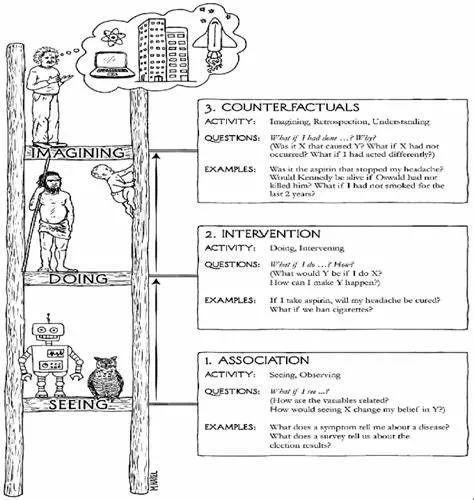
Judea pearl 的因果之梯


事实上，有大量的例子能够让我们找到这种跨层级的因果关系。例如，在遭遇洪水的时候，蚂蚁群体能够互相抱团，形成大蚂蚁球，从而在洪水中漂流。这一过程中，有很大一部分蚂蚁将被水淹没而死亡，可是尽管如此，这些被淹死的蚂蚁仍旧坚持互相抱团，为蚁群的利益而牺牲自己，最终蚁群得以保全。这是我们从生物学现象角度进行的解读，而当我们从因果的角度进行解释时，这件事可以这样表达：当蚂蚁形成蚁球时，个体的意志将被整体的意志替代，随着蚁球的出现，一个新尺度的“自我”和“个体”便出现了。于是，这个“自我”便可以为满足生存的需要，损失一部分蚂蚁。


为了在洪水中存活，蚂蚁抱团成群


或许这种叙述过于拟人化，恐怕有些不真实，那么，让我们来看看下面这个例子。


我们不妨做出这样一个动作，即用自己的手拍打自己的身体，当我们做这个动作的时候，仍旧可以从两个层次观察：在微观层面，这个动作无疑会造成手臂、身体上大量细胞死亡；而从“我”这个整体的人层面看，这些细胞无疑是被“我”制约的。吊诡的是，“我”是由大量的细胞构成的一个系统，假使按常规的因果论（还原论），“我”这个人体的特性是由细胞所决定的，正如“我”会害怕火，是因为细胞害怕火，细胞一被火烧，就会死亡。可是，人们却可以为自己的理想信念做出牺牲，甚至不惜让自己的细胞乃至于全部都被火烧死。显然，这超越了常规的从微观到宏观的因果论，而是从宏观到微观的因果倒置。


我们可以用下面这张图来表示这种情况。通常情况下，我们讨论的因果联系可以看做在蓝色的圈里，个体之间相互作用而产生的，但是，微观的因果解读虽然也可以解释上面的例子，比如人之所以会死是因为被火烧了，蚂蚁之所以会死是因为被水淹了，手臂上的细胞之所以会死是因为细胞的互相碰撞，而这一动作不过是因为神经放电以及信号的传导——所有的这一切都符合物理化学的基本规律，然而这些解释却显得冗余且没有触及到更重要的本质：人可以为了理想信念而牺牲；蚂蚁可以为了整个蚁群而牺牲；“我”存在自我意志，所以可以拍打自己。这些都是因为有一个更高层级的整体，这个整体可以作为一个独立的主体发出“因果之力”，使得因果箭头从整体指向个体：我希望拍打手臂，所以产生了动作，细胞也随动作而死亡。


值得强调的一点是，这里面所讨论的因果与我们通常所说的“因果”是存在定义上的区别的，同样，虽然其与我们的主题因果涌现存在联系，但也同样存在区别。


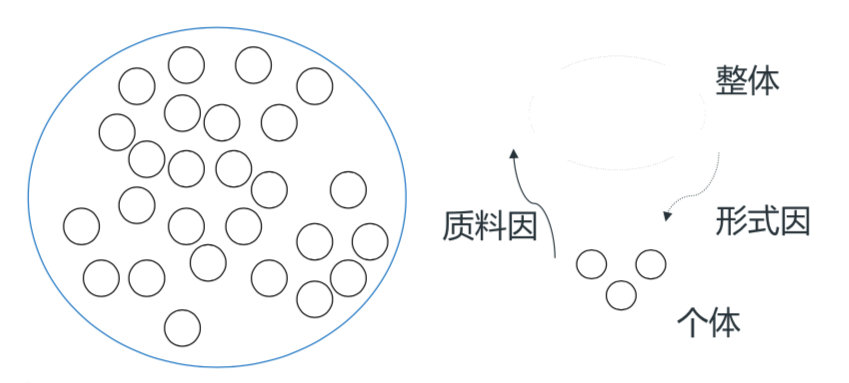
跨层次的因果作用


事实上，早在两千多年前，哲学家亚里士多德便对此有过讨论，他提出四因说，将世界上事物的变化与运动的背后原因（古希腊语：αἴτιον）归纳为四大类。四因包括：
  1. 质料因：即构成事物的材料、元素或基质，例如砖瓦就是房子的质料因；
  2. 形式因：即决定事物“是什么”的本质属性，或者说决定一物“是如此”的样式，例如建筑师心中的房子式样，就是房子的形式因；
  3. 动力因：即事物的构成动力，例如，建筑师就是建成房子的动力因；
  4. 目的因：即事物所追求的目的，例如“为了安置人和财产”就是房子的目的因。

亚里士多德认为，凡感性实体，包括自然物和人造物，都具备这四种原因。

对应到上面的例子，质料因是我们习惯的因果联系，即物质的构成元素会决定整体的性质。同样，在此之外还存在另外一种因果联系，即由物质整体所决定的属性。而我们谈论的现象——用手拍打身体，它的奇妙之处就在于，质料因和形式因发生了复杂的、甚至是混淆的缠绕。

亚里士多德的四因说

除此之外，还有一种更加特殊的因果关系。在电影《黑客帝国》（The Matrix）里，有一个经典镜头便表现了这种因果关系：

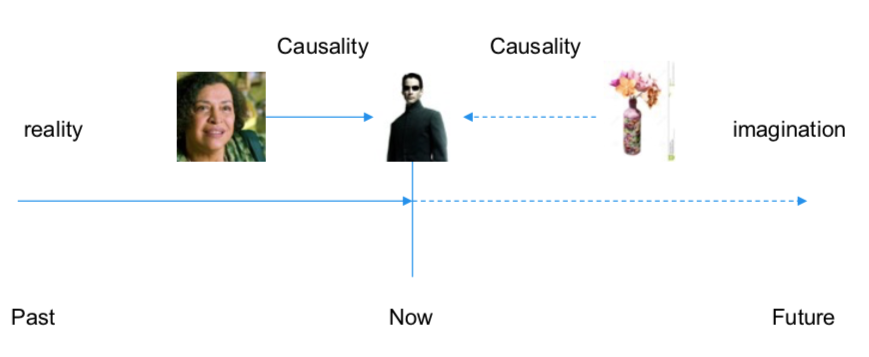
ORACLE: I’d ask you to sit down, but you’re not going to anyway. And don’t worry about the vase.

先知：我就不请你坐了，反正你也不会坐。你别担心那花瓶。

NEO: What vase?

尼奥：什么花瓶？

He turns to look around and his elbow knocks a VASE from the table. It breaks against the linoleum floor.

他一转身，碰倒桌上的花瓶，掉地上碎了。

ORACLE: That vase.

先知：就那花瓶。

Neo: Shit, I’m sorry.

尼奥：见鬼！对不起。

She pulls out a tray of chocolate chip cookies and turns. She is an older woman, wearing big oven mitts, comfortable slacks and a print blouse. She looks like someone’s grandma.

她取出饼干，转过身来。穿着、样子、动静，看上去就像一位邻家奶奶。

ORACLE: I said don’t worry about it. I’ll get one of my kids to fix it.

先知：我说没关系，我会叫那些孩子来还原它的。

Neo: How did you know…?

尼奥：你怎么知道会……？

She sets the cookie tray on a wooden hot pad.

她将饼干放一木盘上。

ORACLE: What’s really going to bake your noodle later on is, would you still have broken it if I hadn’t said anything.

先知：让你觉得更困惑的是，我不说，你还会不会打破那花瓶。


正常情况下，因果序列表现为，先知对Neo说，不用担心花瓶，Neo听见后便转身，结果打碎了花瓶。不过，这里面存在一条奇妙的因果箭头：实际上，Neo头脑中还存在一个想象世界， 当先知与Neo说完话后，Neo便想象到花瓶碎掉的场景，或者说是一种预期，对未来的预期显然还未发生，正是这一预期使得Neo转身，花瓶便被Neo打碎，于是，预期便得以自我实现（Self-fulfilling Prophecy）。似乎，这里面存在一种从未来指向现在的因果箭头，当然，在这个例子中，这是因为人脑存在一个想象世界，不过，这种现象会在很多存在生命的个体中发生，比如虫子会在自己的控制下爬向食物，这里面，正是未来的预期，或者说目的，驱使了虫子的行动。虽然，这种现象普遍存在于复杂系统之中，但似乎我们的因果科学还没有对此进行讨论。

因果涌现

这部分似乎都是在讨论一些哲学问题，不过，我们的因果涌现读书会不会停留在哲学层面上，一切的哲学讨论都是为了引入我们的核心概念：显然，复杂系统存在一些核心问题，同时因果与尺度和层级存在复杂的作用，可是这些重要的问题好像还没有得到回答。

然而，随着科学的发展，我们也有了很多工具，其中的一些使得我们得以从科学的角度来解释这些问题，比如因果涌现的理论框架、粗粒化（Coarse-Graining）、整合信息论（Integrated information theory）、机器学习驱动的重整化（Renormalization）、以及自指动力学等一系列重要的思想、方法和技术。这将是接下来要讨论的重点。




四、粗粒化的出现与意义




前面介绍了不同的因果涌现现象，我们不禁要问，有没有办法从科学的角度来研究它？答案是肯定的。不过，在进入因果涌现框架之前，我们还需要做一些必要的技术准备。


首先，我将介绍一种关键的技术或者说技巧——粗粒化（Coarse-Graining），正因为有了这一工具，我们才能够从科学的角度讨论因果涌现。


粗粒化是一个来源于统计物理的概念，其本质是对一个系统进行粗糙尺度的描述。粗粒化的其他表达包括池化（pooling）、下采样（down-sampling）、尺度缩放（scaling）。实际上，这些概念表达的都是对一个系统或者客观事物进行尺度缩放的操作。


杰弗里·韦斯特（Geoffrey West）写的《规模》（Scale）一书便专门研究了这一概念。他在书里告诉我们，大自然里，在空间、时间这些最基本的描述方式之外，还存在一种维度的描述，这种描述同样非常本质，但我们对其知之甚少——这便是尺度。


杰弗里·韦斯特（Geoffrey West）。参看《Geoffrey West 重磅演讲实录 | 地球未来：生物体、城市和公司的生命、生长和死亡（内附视频回放）》


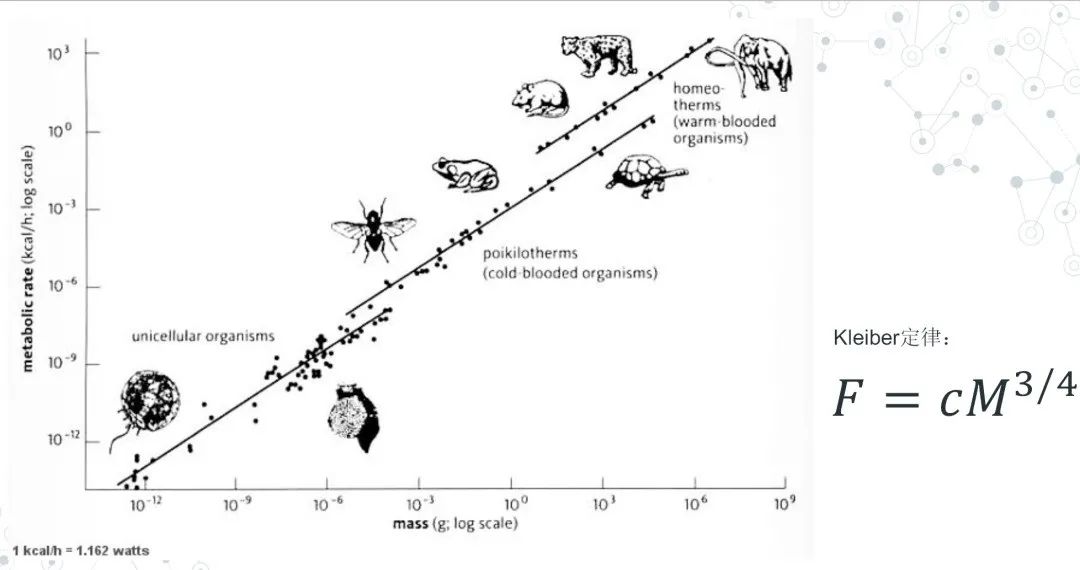
实际上，有很多特性只有通过尺度缩放才能发现。比如克莱伯定律（Kleiber’s law）：当我们对自然界的生命体进行从小到大的缩放时，可以发现一种新的规律，即生物体的基础代谢率水平与体重的¾次幂成正比。这一规律横跨了数十个数量级，无论是单细胞生物、冷血动物还是哺乳动物，都遵循同样的法则。


克莱伯定律表明，生物体的基础代谢率水平与体重的3/4次幂成正比。


事实上，所有模型都是对真实世界的粗粒化描述。


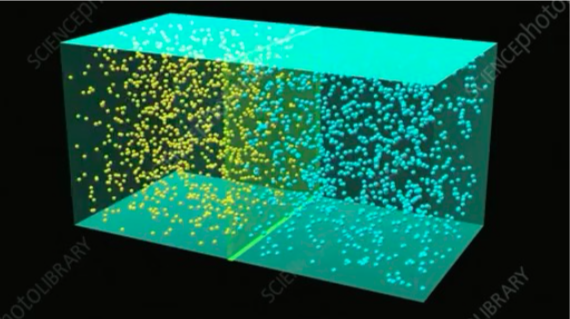
另一个非常典型的例子是统计物理中的案例。在微观层面，我们难以对分子的运动进行描述（比如气体分子的运动就是无规则的布朗运动），不过，统计物理学家使用了一种非常特殊的操作，即将整个气体系统用几个宏观量来表达，比如压强（P）、温度（T）、体积（V）。当我们忽略分子间的细节，整体的规律便会显现出来。显然，统计物理就是一种粗粒化的描述，当我们从宏观的角度分析时，规律便会非常清楚，并且，这也是一种最强的因果联系。这便是我们因果涌现的核心思想，即站在不同的层级，可以抽象出不同的因果关系。


对于大量无规则运动的气体分子，如果忽略分子的细节，整体的规律便会显现出来。比如理想气体分子可以用方程 PV=nRT 描述。


粗粒化的历史可以追溯到统计力学之父——玻尔兹曼（Boltzmann）身上。在他的墓碑上，刻着统计力学的核心概念：S=k㏑Ω（玻尔兹曼熵），而熵的定义，便与粗粒化有着紧密联系。我们可以从下图进行理解：当我们从宏观态描述时，每个小球可以划分到左边、右边，那么，宏观态的描述便是最左边一列，中间是小球的微观态，不仅有左右大区域，还有很多格点。比如第一种宏观态对应非常多种微观态，大约是706个。我们对其取自然对数，便是玻尔兹曼熵。实际上，玻尔兹曼熵便是我们进行粗粒化操作后所忽略的信息量。而把熵的概念引入后，统计物理这一学科便得以建立，宏观热力学特性便可以从微观角度进行解读。


玻尔兹曼熵与粗粒化有紧密联系





五、因果涌现：

信息论下使用粗粒化测量因果强度




1、因果涌现的整体思想


在因果科学以及粗粒化的基础上，我们认识到，对于一个系统，可以有不同尺度的描述，这便是不同尺度下的新的因果关系。现在，让我们聚焦在因果涌现上，看看它的框架究竟是如何建立的。


因果涌现理论的构建者是埃里克·霍尔（Erik Hoel），一名哥伦比亚大学的理论神经科学家。不过，在我看来，这套理论不仅可用于神经科学，它同样可用于复杂系统。


Erik Hoel，哥伦比亚大学的理论神经科学家


因果涌现的基本思想，是在两个不同的尺度对系统进行描述。其基本思想是统计力学，站在宏观尺度时，就会看到明确的因果规律。因果涌现的具体设计如下。


我们先看底下的微观层次，可以认为，微观层次是这个世界的本质，比如现实里空气由一大堆气体分子小球组成，气体分子会遵循气体动力学，我们把它叫做微观因果机制或者微观的动力学机制（f）。但是由于在微观层面上存在着大量的随机性，或者是混沌特性，即混沌系统中尽管顶端力学机制是确定的，但仍然存在很强的不确定性。所以这时候，我们认为，它的因果联系、因果特性非常弱。（这里所指的强弱，在后面将有严格的数学定义，即使用互信息进行定量刻画。）于是，微观上便只能观察到随机的、不确定的机制，因果联系也非常弱。


而为了获得更确定、更有联系的因果描述，我们作为观察者，便进行粗粒化操作，把微观态的东西映射成宏观态，使用大尺度来描述。具体操作正如我们刚才讲过的分子小球，对应到这里就是用上面的彩色方块表示下面的彩色小球。当然，我们暂时没有考虑时间尺度上的粗粒化。


进一步地，我们假设，每一个时间步都可以做粗粒化操作，而下一个t+1时刻，也可以得到一个粗粒化的宏观态。那么，我们便可以在宏观尺度上，看两个时刻的变化，而这一对应机制，便是宏观态下的动力学机制（F）。


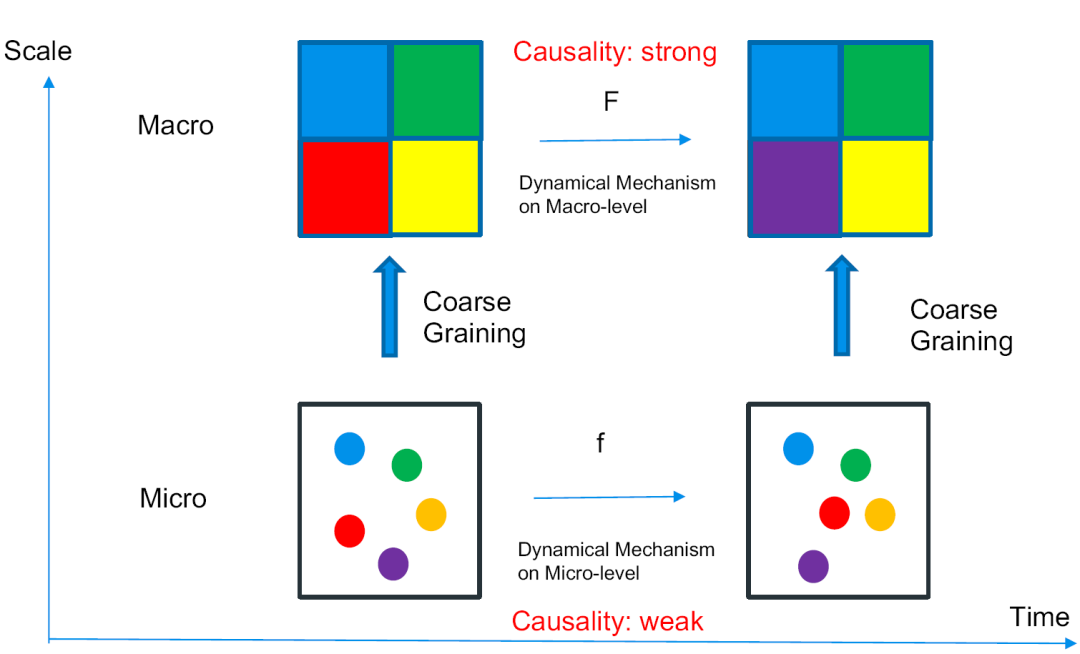
通过粗粒化操作，把微观态映射到宏观态。微观上因果联系非常弱，宏观上则具有非常明确的因果规律。


为什么可以这样看呢？原因很简单，整个系统是由每一个微观态一一映射过来的，显然，在微观态，确实存在一种动力学机制，尽管它有不确定性。所以到宏观以后，显然两者之间也会有一定联系。


这个时候，神奇的现象出现了，即有可能在某些特殊的情况下，至少我们能构造出来这样一些特例，在宏观态的描述中，对应机制有可能变成一个因果联系非常强的动力学。也即，在宏观角度去看，它具有非常明确的因果规律。这一例子并不难理解，比如布朗运动就属于这种情况。


这便是因果涌现所表达的意思，而宏观的因果规律，也正是因果涌现。


2、因果涌现的具体操作


因果涌现具体的每一步操作，都可以用数学进行严格刻画。


首先，让我们看一看它如何刻画动力学。对动力学进行描述的机制在微观和宏观上都至关重要，而因果涌现框架则是使用马尔科夫动力学作为动力学机制的一套描述工具。选择马尔科夫的道理很简单，如果假定我们的世界服从物理规律，而物理规律都是马尔科夫的，也即上一时刻的动作（状态）能完全唯一地决定下一时刻的动作（状态）。


在马尔科夫框架下，动力学实际上就成为了马尔科夫转移矩阵。因为我们假设，尽管系统可以是多体的，但是这里面的状态是一个离散化的分布，每一个小球只有0或1这种离散的状态，所以整个系统的状态就可以进行离散化的描述，于是系统的状态转移，也就是它的动力学，就可以用一个马尔科夫链或者说马尔科夫矩阵来表述。


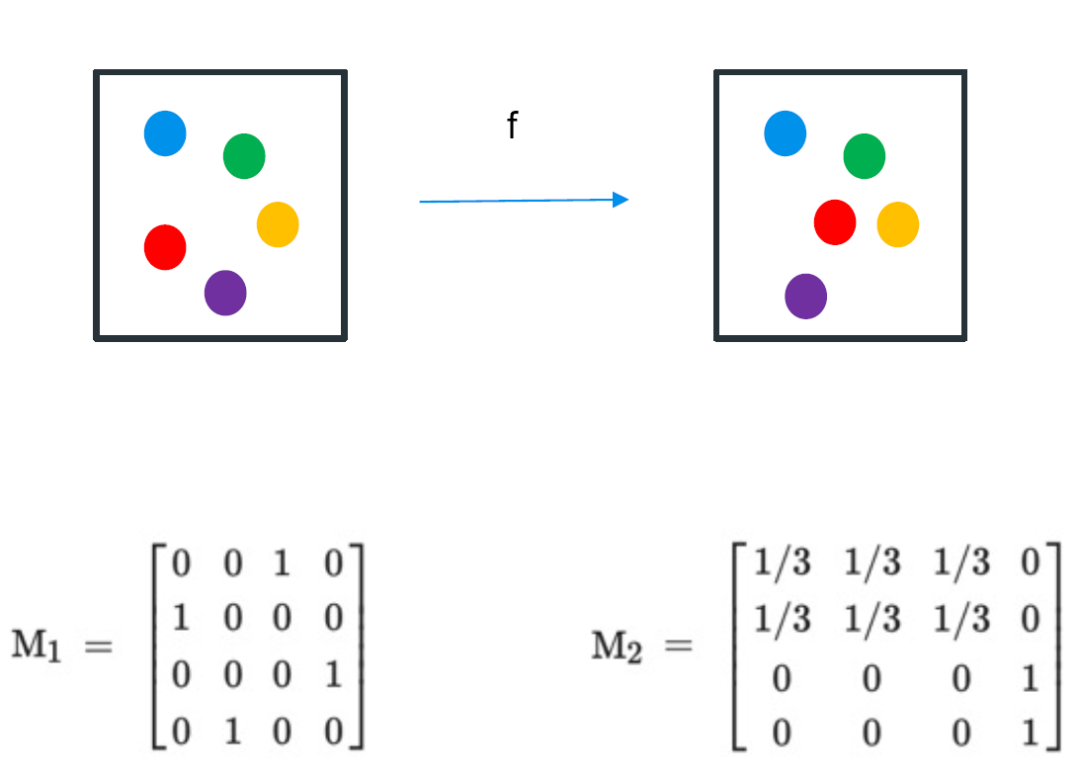
两个马尔科夫矩阵的例子


那么，针对这样的马尔科夫动力学，什么是它的因果机制的强弱呢？我们又应该如何测量计算它呢？在这里，它采用了互信息的方式来刻画，也即上一时刻的分布与下一时刻的分布之间的互信息作为因果强弱的度量。


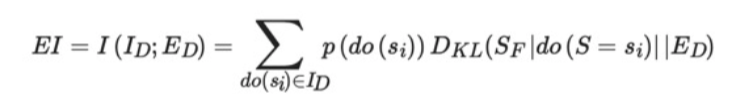
用互信息作为因果强弱的度量


同时，它可以进一步拆解为后面的公式。后面的公式所解决的问题是，如何测量动力学机制即因果联系是确定的还是随机化的。这可以通过干预（do算子）的方式进行，假设我们的干预按照某一个分布ID（通常情况下，ID是均匀分布的，也就是在T时刻，所有微观的状态都是等概率分布的）。在每一个干预情况下，因为它有多种不同的微观态，所以都会有一个干预以后的状态，其概率分布和它在不做干预的时候，或者说在上一时刻在自发条件下演化所得到的下一时刻的状态（ED）进行比较，刻画二者之间分布的距离（DKL，KL散度）。最终，通过所有可能的干预动作进行加权平均后，我们便得到了二者的互信息。


不过，虽然这一定义具有一定的合理性基础，但能否作为因果关系的最好度量，恐怕还值得商榷。例如，对于M1这样的马尔科夫矩阵，我们可以看到它在每一个微观状态下，都以概率1转移到下一个微观状态，显然，这是一个完全确定的动力学，而它的互信息 EI 也是比较大的。


我们不妨比较几种不同的这种系统，当然，我们暂时还没有牵扯到宏观态，我们只是讨论对于一个马尔科夫转移矩阵，应该如何刻画它的因果联系的强弱，目前还没有引入粗粒化操作。


如下图，下面的黑白格是关于矩阵的表述，左边是输入的干预。具体的干预操作，就是让它做均匀分布。在上面我们给出了三个不同的马尔科夫一步转移矩阵，是下面的马尔科夫矩阵的加权有向图。这样的话，三个不同的系统会产生三个不同的马尔科夫链。显然，有的系统是完全确定的动力学（第一个），有的系统是完全随机的动力学（第三个），有的系统部分确定、部分随机（第二个）。接下来我们按照上面所讲的互信息进行度量，确定性动力学的 EI 最大（2 bits），完全随机动力学的 EI 则最小（0 bits）。


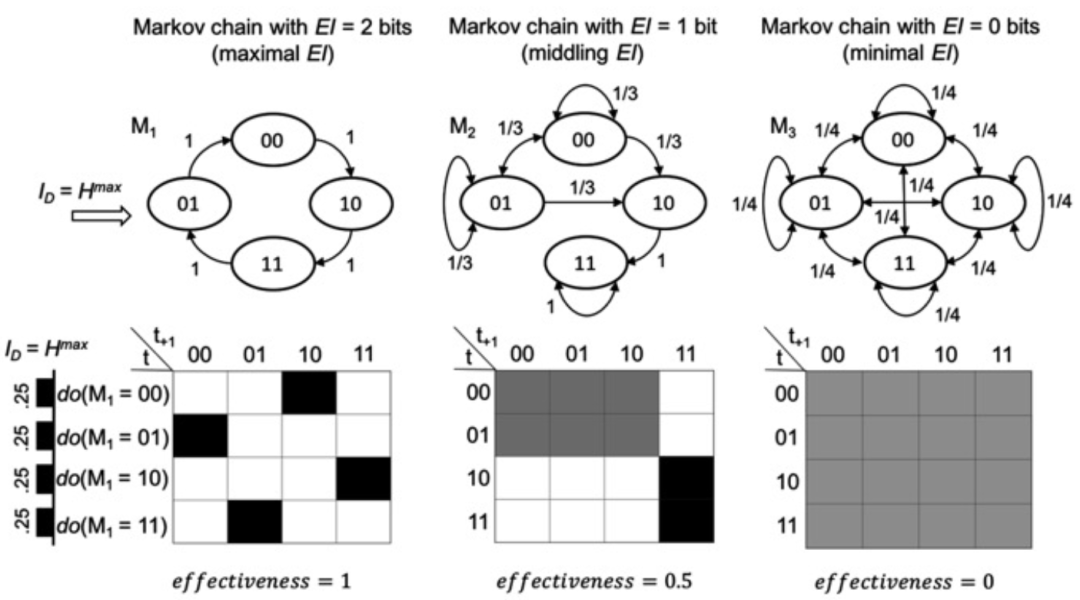
三个不同的系统产生三个不同的马尔科夫链。（左）具有确定性动力学的系统 EI=2 bits，互信息最大；（中） 部分确定、部分随机的系统 EI=1 bit；（右）完全随机动力学的系统 EI=0 bits，互信息最小。


接下来，我们引入第二个操作，即粗粒化。


让我们先来看一个例子，当我们对一个系统的微观态进行粗粒化时，它的马尔科夫动力学就有可能从一个完全随机的动力学变成一个完全确定的动力学。


下图左边是微观态下的马尔科夫转移矩阵，这个系统里一共有8个状态，这个状态的动力学比较特别，即在前7个状态下，完全等概率的随机转移，不过，第8个状态则是完全确定的动力学，即停留在第8个状态下。当然，这是一个抽象的例子，在现实世界中并没有对应。


而对于这一动力学，我们可以进行粗粒化操作，即把前7个微观状态映射为一个宏观状态，我们将这一宏观状态称作随机态，第8个状态映射为另一个宏观状态，将其称为确定态。此时，宏观状态的描述只有两个，一个是随机态，一个是确定态。此时，动力学也自然确定了，即都是由“自己到自己”的变化，而其互信息也得到最大化。


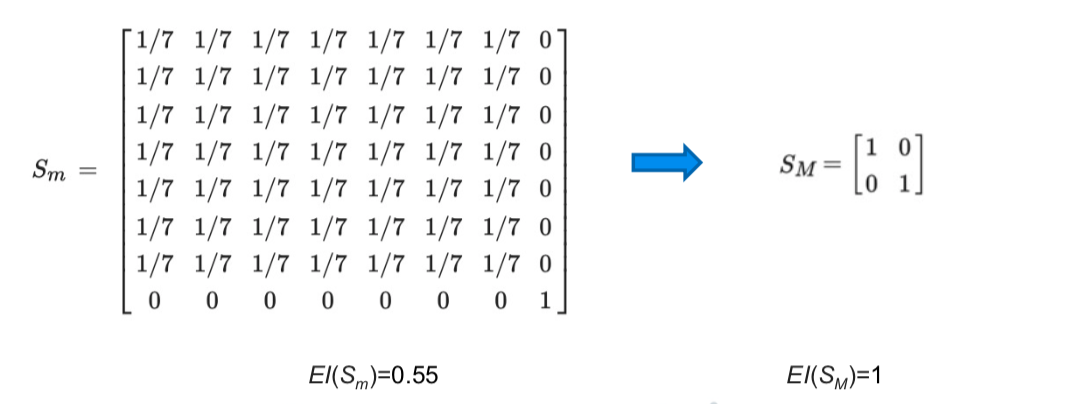
粗粒化操作下，微观态下的马尔科夫转移矩阵 Sm 映射到宏观态下的矩阵 SM。系统的动力学发生变化，互信息变大。


以上，便构成了因果涌现的基本框架。


当然，上述分析的粗粒化只是对状态的粗粒化，还没有牵扯到多体、复杂系统，在2013年一篇PNAS文章*里，说明了如何对多体系统进行粗粒化描述，即同时对节点进行粗粒化。当然，粗粒化也可以在时间尺度展开，我们把此处留到后面的读书会进行展开。

* E. P. Hoel, L. Albantakis, and G. Tononi. “Quantifying Causal Emergence Shows That Macro Can Beat Micro.” Proceedings of the National Academy of Sciences 110, no. 49 (December 3,2013): 19790–95.


3、从粗粒化到因果涌现的若干模型


接下来，我们进行一些讨论。


第一个问题便是，宏观的因果是一个全新的东西吗？事实上不是的，宏观的因果蕴含在微观态的因果机制中，即粗粒化策略给定的情况下，宏观态下的因果联系就成为完全确定化的一个过程。这也正是论文出来后大家对他的一些争议，有人说，其实论文中所谓的宏观因果，并非完全的涌现，因为它被微观动力学所决定，这么看来，论文中的宏观因果只是揭示了微观因果的一些特性而已。


另外一个问题则是粗粒化操作。实际上，这一框架被人批判的另一重要原因，便在于粗粒化的操作非常微妙（tricky）。显然，有些粗粒化操作会使得问题变得更加无意义（trivial），比如下图的粗粒化，将所有的微观态作为一个宏观态，就完全没有价值，然而它确实增强了因果联系。文章的理论框架看起来并没有排斥这些看起来比较极端的操作，原因在于我们的粗粒化操作并不存在约束，似乎完完全全是拍脑袋决定的。


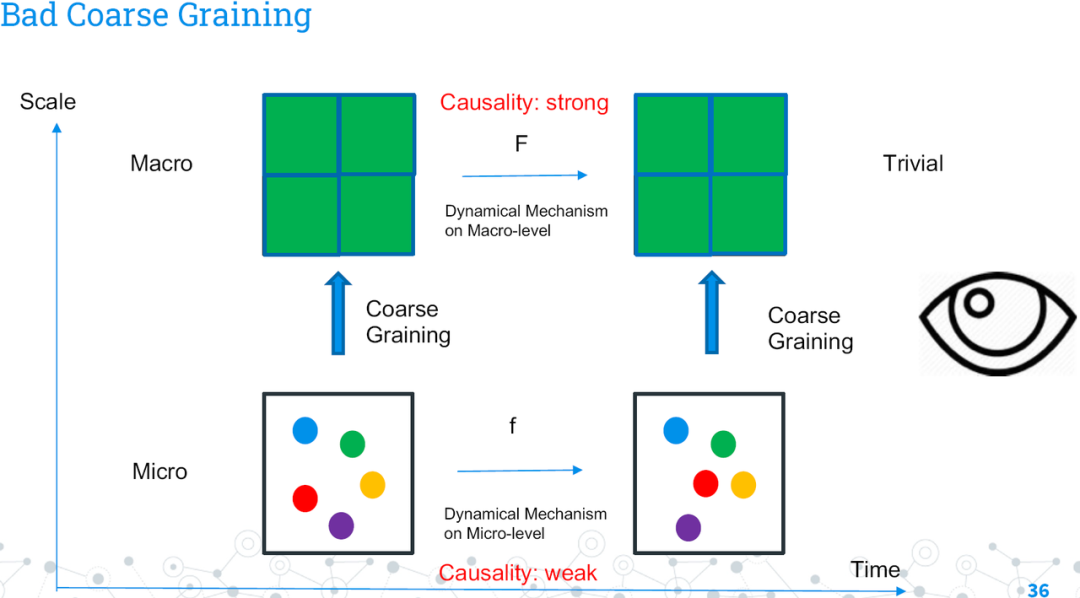
有些粗粒化操作是无意义的


对于第二个问题，实际上目前有一些进展。近几年，随着机器学习的进步，我们发现可以相对客观地来定义粗粒化操作。下面几篇文献展示了运用机器学习方法来自动学习映射，使得粗粒化操作具备有效且合理的约束，其中两篇是由我们集智俱乐部的成员、中科院的王磊老师和核心成员尤亦庄大神写的。


这些文章指出，通过一系列规则，如使微观态与宏观态的互信息最大化，利用可逆神经网络等，通过机器学习的训练，可以得到高保真且恒等的映射。至此，虽然我们无法保证映射的唯一性，但起码粗粒化的操作有了极大的约束，从而避免出现无意义的操作。不过目前，上述两个领域并没有很好的结合。


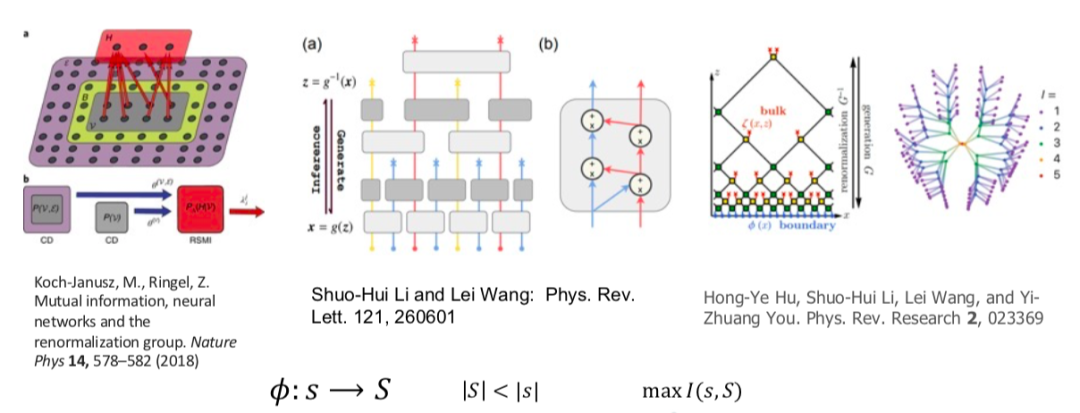
运用机器学习的方法自动粗粒化


从另一个角度看，机器学习学术社区已经在因果涌现框架下进行了丰富的尝试，比如很早就出现的自编码（auto-encoder）框架，就是对因果涌现的另外一套表述。


我们来看一看自编码的策略。自编码的本质就是要训练一个神经网络，可以对数据进行压缩，而神经网络唯一的学习目标就是把输入的信息X压缩成X’，使得在给定X’的情况下，经过反向操作，可以原封不动地恢复X的信息。这就是自编码器的精髓。所以我们发现，无论数据是图像、语音还是其他，经过自编码器操作以后，可以很好地进行压缩。


表面上，自编码器与因果涌现没有什么联系，但稍微进行变换，它却能和因果涌现完美对接。通过一个小小的改变，便能描述因果涌现框架下的动力学：只要把自编码器中的输入（input）变成上一个时刻的微观态，输出（output）变成下一个时刻的微观态，此时，编码的过程就是宏观的描述。当然，这里面还需要做一步操作，即在中间拆开，变成两部分，此部分仍旧需要一个小的神经网络。完成这一步后，整个自编码的框架，就变成了因果涌现的框架。


站在这个角度，宏观因果涌现就成为一个编码压缩的过程。这一思想在霍尔2017年的文章里面便提到了。他认为，实际上因果涌现可以看成一个信息的通道（channel），就是传播（communication）的一个channel，只不过，他认为宏观态下的因果涌现也是编码，也是信息的通道，因此我们要把这个信息通道的互信息最大化。


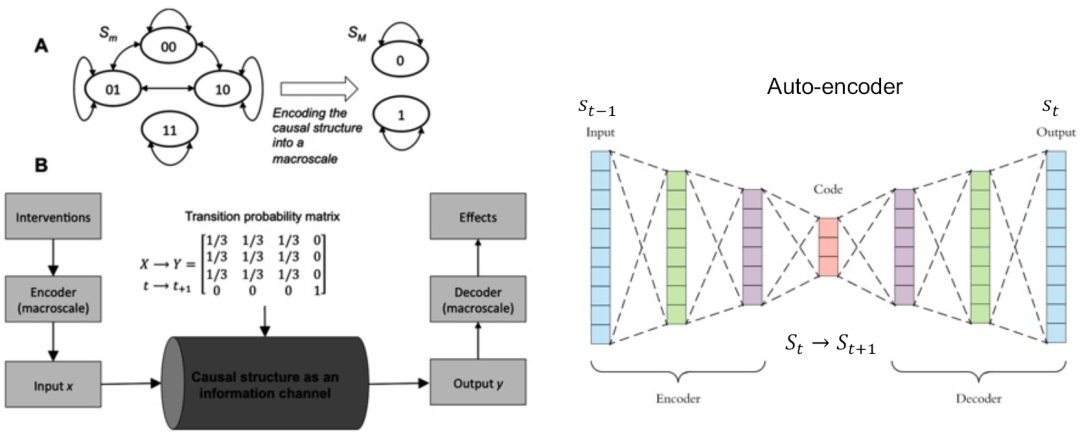
自编码过程


所以总结来看，从机器学习的角度来说，我们完全可以用数据驱动的方式训练并发现，整个从微观到宏观以及从宏观到下一时刻的因果关系。这也正是我的团队正在进行的多尺度建模框架，即数据驱动下因果涌现的自动发现。


更进一步，我们可以将因果发现（causal discovery）这一在因果社区里非常核心的话题与我们的因果涌现框架进行结合。传统的因果发现往往只在一个层级，也就是微观态下，用数据驱动的方式去发现不同主体、不同节点、不同变量之间的因果关系，而有了粗粒化操作后，我们便可以在宏观态下发现因果联系，从而实现不同尺度乃至跨尺度的因果发现。


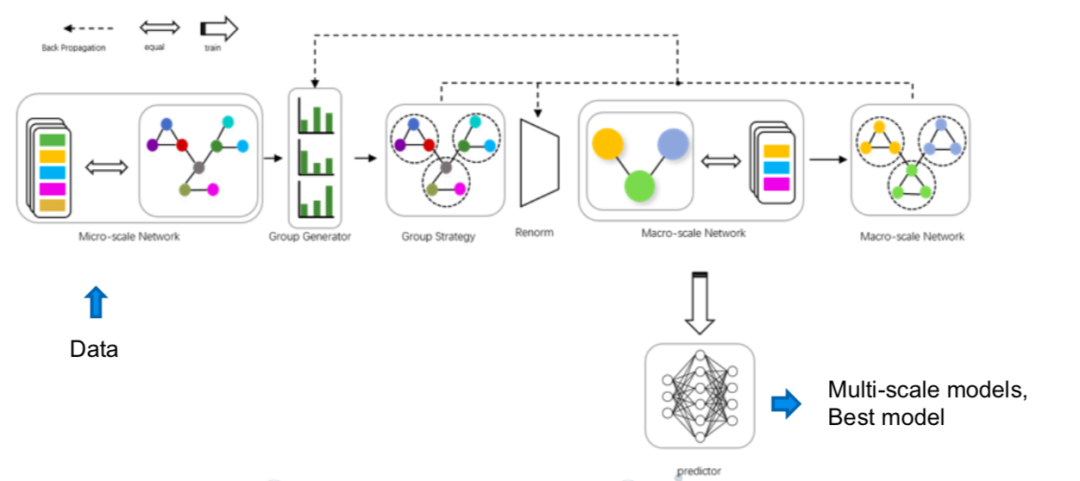
多尺度建模框架


    



六. 意识与自我意识




在这一部分，我们将进入更加深层次的问题，即意识和自我意识（Consciousness & Self-awareness）。


目前，人们对于意识的认知包含三重涵义。第一层面是无意识加工，即我们可以接受外面的信息，并且对这些信息做出反应，不过，这个层面的运算量可以很低。第二层面是总体可用性，也就是意识有这么一个特点，即唯一性，每一时刻我们的头脑基本上只能聚焦在一个事物身上，这也就是所谓的注意。当我们看东西或者想东西，基本上不能一心二用，所以存在唯一性。第三层面就是自我监控，这里便涉及到了对自我的感知，我思故我在，我能明确的知道我自己的这个存在。我们的讨论将主要集中在第二层面以及第三层面。


1、整合信息论


首先，让我们来看看整合信息论。整合信息论是 Erik Hoel 的老师托诺尼（Giulio Tononi）提出来的一套关于意识整体性的理论。


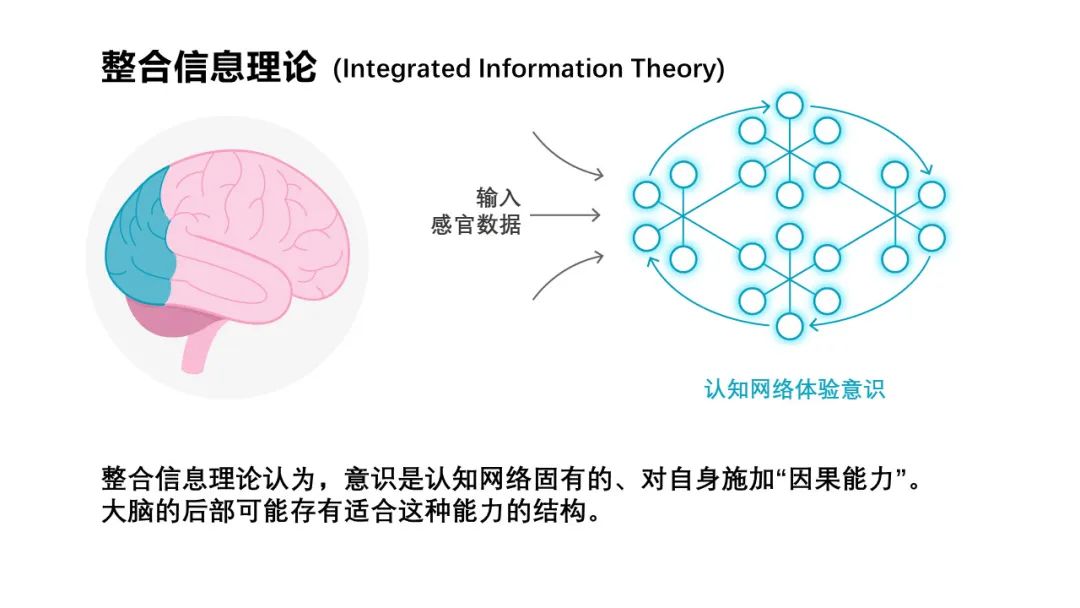
托诺尼的目标是用这一理论估计复杂系统是否存在意识。当然，这一事情的难度太高，所以他稍微降低难度，即通过计算所谓的意识度，也就是他所说的φ的大小来估计。他认为，一个复杂系统要想具有意识的能力，必须拥有整体性，即去掉系统的一部分以后，系统便不完整，从而没有办法处理复杂的信息。所以，所谓拥有意识的复杂系统，一定是一个不可分割的、整体性的存在。


具体来讲，托诺尼定义了一个最大指标，其涉及到如何对系统进行划分，从而找到一个最小的不可再分的集团，当我们找到这一集团后（某种程度上类似于复杂网络中寻找最大连通集团），其任意一部分都与整个系统存在紧密联系，同样，这一紧密联系将通过前面所说的互信息进行刻画。即一个有意识的、意识度很大的体系具有如下特性，其任意一部分都与其他部分存在非常强的因果联系。这样的一个体系便被称为整合信息也即信息量最大的一个体系。


所以，我们可以把整体分为各个部分，即各种可能的切分，再看各个切分部分之间的互信息，将所有组合的互信息最小值做为整体的意识度或者整合信息量的度量。


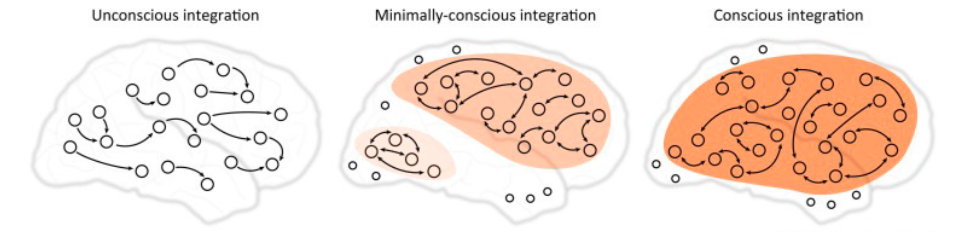
计算意识度φ来估计复杂系统是否存在意识


总之，托诺尼将意识的问题转化为φ进行刻画。其实这并没有太多新的东西，不过计算φ最麻烦的一点在于，需要遍历所有可能的划分，且每做一种切分，都计算其中的互信息，以使得最小互信息的值能够被找到。此时当最终的φ越大，系统的整合性就越强，即彼此因果联系越强，意识程度也越高。


当然，他们尝试了一些实证策略，比如对人大脑神经元的活动进行测量，从而计算时间序列中的互信息。他们的结果显示，当人清醒且有意识的时候，φ值就比较大，脑区的最大连通集团也刚好对应了自主神经系统（与意识有关的系统）。对于脑瘫痪或者无意识的人进行测量，则会发现φ值比较小。因此目前整合信息论被人们所接受和认可。不过，不幸的是，亚利桑那大学研究人员发现，φ的度量存在漏洞，这些我们将在未来的读书会展开。


2、自我意识


接下来我们将谈谈，一个系统在什么时候能够意识到自我的存在。这与我和我们集智俱乐部长久以来追索的一个大问题密切相关，这个问题也和我们一开始谈到的冯·诺依曼问题存在密切联系，这便是自指。自指早期的讨论来源于《哥德尔、艾舍尔、巴赫——集异璧之大成》这本书，我也强烈推荐大家去阅读它。（解读GEB的视频 https://campus.swarma.org/course/51）


《集异璧之大成》


所谓的自指，类似于这样一句话：


这句话是错的


自指可以单独作为一种现象进行讨论，不过，又因其与生命、意识等具有十分紧密的联系，所以我们常常联系起来看。让我们回到这句话，它在谈论它自身，并且它判断自己是错的，当我们去理解它的时候会发现，它既不是错的，也不是对的。对于自指问题，我们集智网站上有大量的视频对其进行讨论。


实际上，这样普通的一句话，却引发了数学史上的第三次数学危机，且它跟一系列重大课题，包括康托尔的集合论、罗素悖论、哥德尔定理以及图灵停机问题，甚至人能否制造出人工智能等，都有着非常深邃的联系。比如彭罗斯说，人不可能造出人工智能，因为人工智能存在一个致命的命题——无法判断的自指命题。即在整个理论框架下，纯机械化的系统里，会存在一些漏洞、黑洞，这些黑洞必须要靠外界的人去给它帮助，而它自己却不能够发现。（比如哥德尔指出，存在某些无法在数学体系内证明的真理）这是否证人工智能的一个理由，在这块我不过多去展开。


自指现象与数学中的许多重大问题具有深刻联系


我将对另一个问题进行展开，这一问题对应了冯诺依曼的发现，即自复制自动机的工作。我觉得目前我们远远地忽略了它的价值，它事实上至关重要。让我们再来回顾冯诺依曼的问题，他发现很多系统存在两极分化，当系统的复杂度没有超过某一个阈值，那么这个系统就会不断降级，不断衰败以至于死亡，而当系统的复杂度超过那个阈值的时候，这个体系就会自发的不断升级进化，以至于达到越来越高等的程度，那么，复杂度的分水岭到底是什么啊？这一问题在书里有明确的回答，他认为就是自复制的能力。对于现实世界的生命，具备自复制能力就代表能够自动升级，而当时的人造系统却无法达到这一点，于是，它便会不断降级。


自我复制的细胞自动机


实际上要完成自复制的过程是非常困难的，甚至于这是一个看似不可能的事情：一个系统要把自己全部复制出来，这意味着该系统必须能够获得自我底层的源代码，且靠执行它从而将自我复制。但实际上它却是可能的，因为数学家克莱因（Stephen Cole Kleene）使用数学语言将其证明出来了，当然图灵等人也做过类似贡献，这些科学家证明，这件事情确实可以发生。让我们看看一条最相关的定理：克莱因第二递归定理。


克莱因第二递归定理是说，对于任意的程序F，总存在一段程序代码c，使得我们执行代码c的结果完全等价于把源代码c作为数据输入给程序F执行的结果。这意味着，只要是一个遵循定理而精心设计的程序，那么就可以不依靠外界，任意修改自身的源代码，也即不断让自己升级优化。定理提到任意的程序F，那么，F便有可能是具备复制、打印源程序的程序，因此，自复制机器便成为可能。


让我们进一步看看这些实例。比如打印自己源代码的程序，也被称为蒯因程序。


蒯因（Willard Van Orman Quine）和蒯因程序


下面这句中文就是精髓：


将引号中的话抄一遍，再抄在引号里，再画一个句号“将引号中的话抄一遍，再抄在引号里，再画一个句号”。


用数学语言来表示就是：



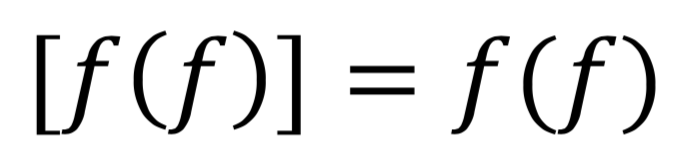
当蒯因代码作为克莱因第二递归定理中的F时，便存在如下设计，即将自打印程序与通用模拟器，再加上一些输入输出操作（即和外界进行互动），这三者结合在一起，便构成了一个特殊的程序——自我反省的程序。这类似于我们可以在大脑里想象我要做什么事情，由此，自我反省程序便成为自我意识的最小内核。


自我意识 = 自我反省 = 蒯因程序 + 通用模拟器 + 输入输出


很可惜，很多年了，人们一直没有将其做出来，而后来我才知道，LSTM之父 Jürgen Schmidhuber 也提过类似的构造——哥德尔机。哥德尔机可以对自己的源代码进行修改，所以我认为，哥德尔机与自我反省的程序是同构的。现在，我们可以保证其存在性及可行性，但是真正的智能是否为这一体系，暂时还无法进行判断。


那么，如何从外在表现来发现具有自指结构，特别是具备自我反省的结构呢？我认为，借助因果涌现和机器学习的框架，在当下时间点上，我们已经具备比较充分的可能性。即，自指的研究，完全有条件进入实证层面。这个后面再详细介绍。


    



七. 重整化




我们最后再介绍一个强有力的工具——重整化（Renormalization）。前面我们介绍了一个与重整化特别相似的概念，即粗粒化，而在很多文献里面，这两个概念又经常混用，以至于模糊不清。但我在这里把二者分开了，将重整化特别定义为包含了标度对称性假设在其中的粗粒化操作。


粗粒化，仅仅做宏观尺度的描述，而重整化，则要在粗粒化的前提下做对应，也即找到宏观层面和微观层面相互呼应关系的建立，这才是所谓的重整化的内容。


我们来看一些具体的例子，比如分形，在计算分形维度的时候，我们进行的便是重整化而不是粗粒化。具体操作分为两步，第一步，将原本的三角形边长放大两倍，第二步则是计算扩大的几何体与原有几何体的相似部分如何对应，即扩大后的面积变为原来的3倍，边长变为2倍。于是，对边长和面积同时取对数，其比值就是分形维度，这个过程就是重整化。

计算分形维度的过程即是重整化


我们再看一个例子，它体现了重整化操作的实用性，这就是逻辑斯蒂映射。我们都知道，逻辑斯蒂映射就是一个离散的动力学。



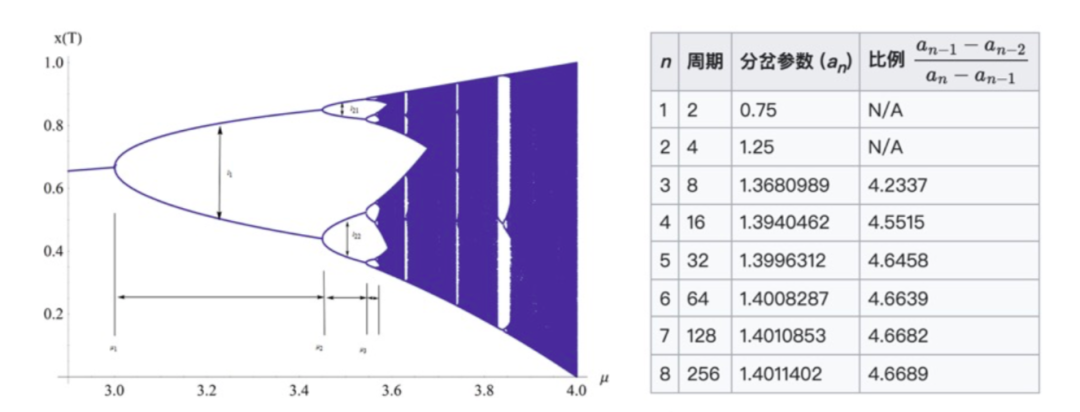
这一动力学具备分形的特性，当我们将动力学的吸引子画成随 λ（在下图是μ）而变化的相图，可以发现它具备分形的结构，根据这一结构可以计算出费根鲍姆常数，即两个分叉彼此之间的宽度两两作差后取比值，当n趋近于无穷大时，其会趋近于一个常数。而费根鲍姆常数是可以通过理论推导出来的，具体过程就是通过重整化操作，即粗粒化后比较宏观尺度与微观尺度两套映射法则之间相似的地方，由此可以建立系数的联系，于是，便可以计算出费根鲍姆常数。


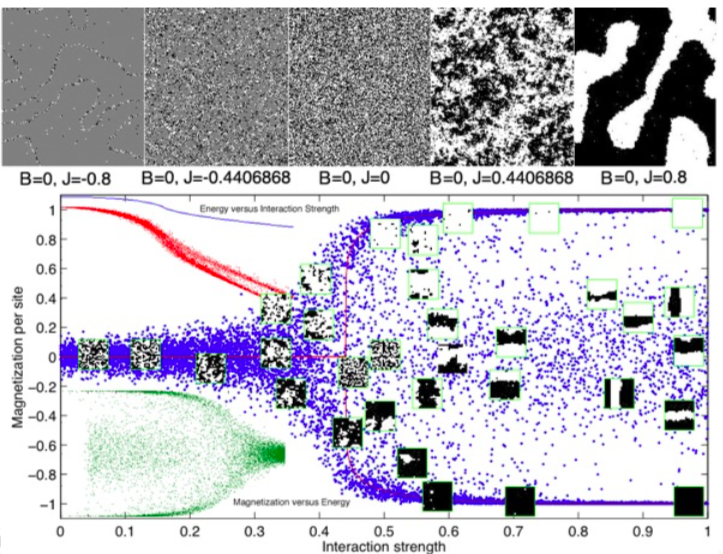
逻辑斯蒂映射的分叉图与费根鲍姆常数。推导费根鲍姆常数的过程也是重整化操作


第三个例子就是伊辛动力学。伊辛模型研究的是一堆小磁针在温度达到临界水平的相变。此时，有各种各样的标度指数在其中出现，比如计算特定图形的分形维度，也可以计算两个小磁针之间的相关系数，相关系数会按指数、幂律的形式分布。整个体系的行为充满了各种各样的自相似特性。但是问题的关键在于，如何求解这些幂律指数，如何从理论的角度进行推导，同时如何推导临界相变的温度。


伊辛模型的重整化


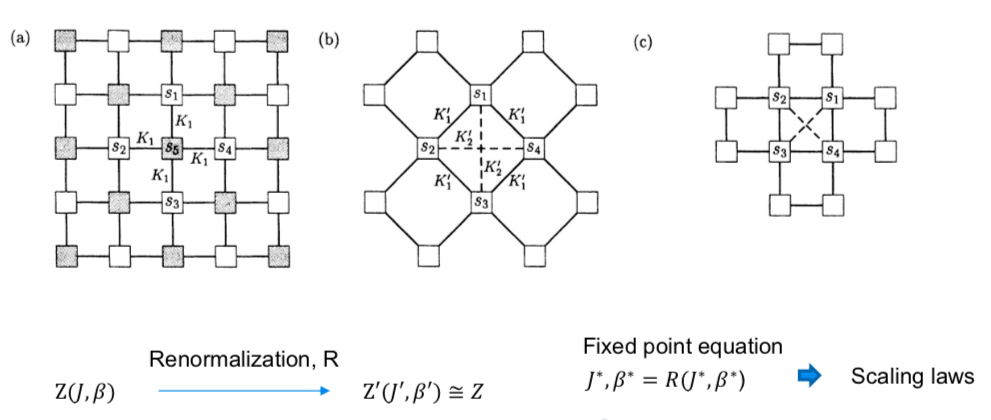
上述都是非常困难的问题，虽然统计物理有多种方法求解，不过最漂亮的一种是重整化的方法。思路如下：将伊辛动力学的自相似特性作为假设、公理引入，从而根据自相似性找出这些参数彼此之间的映射关系，最后我们求解不动点方程，由此便可求出精确的临界相变参数值，而根据这一方程，我们还能找到伊辛模型上一系列的临界指数。


伊辛模型的重整化。参看《尤亦庄：深度学习和重整化群 | 因果涌现读书会第二期》


最后，我们可以将重整化与因果涌现对应起来。重整化意味着，宏观态的动力学与微观态的动力学需要保持一致性，这样，我们就使得整体框架成为重整化而不是粗粒化的。即，关键的变化发生在宏观态的机制由一开始的不同的F变成了与微观态一致的f。看似改变很小，但意义已经完全不同。有了重整化的框架，我们就可以建模自相似动力学系统，这离自指仅仅只差一小步。这一步就在于，宏观态与微观态的粗粒化操作无法在系统内进行，必须要外界“观察者”的加入，也即我们需要定义粗粒化操作——由一个外在的存在来定义，而不是系统内部进行。


自相似动力学建模


真正的大脑便解决了这一问题。大脑的粗粒化机制并不需要外界的加入，其就存在于大脑本身。这意味着我们的自我意识一定存在于大脑的特定区域而不是大脑外，这正是我们自我就足以想象“我”能够走出房间，可以做各种动作，对未来进行一系列想象。而这些复杂的思考都内嵌于大脑内部，这也正是我们的动力学系统所差的一点。



终于，我们将所有的问题连接在一起，我们发现涌现、复杂性阈值以及因果的联系，同时我们有望借助重整化、因果涌现、自指、重整化等一系列工具与理论框架来解决这些问题，二者的组合将使我们有可能回答一些终极问题，这也正是我这次讲座用生命与意识之谜这个大标题的期待！



因果涌现读书会


跨尺度、跨层次的涌现是复杂系统研究的关键问题，生命起源和意识起源这两座仰之弥高的大山是其代表。而因果涌现理论、机器学习重整化技术、自指动力学等近年来新兴的理论与工具，有望破解复杂系统的涌现规律。由北京师范大学教授、集智俱乐部创始人张江等发起的「因果涌现」系列读书会，将组织对本话题感兴趣的朋友，深入研读相关文献，激发科研灵感。


读书会线上进行，8月14日开始，每周六上午9:00-11:00，持续时间预计 7-8 周。


报名方式：

扫码报名

第一步：扫码填写报名信息

第二步：填写信息后，进入付款流程，提交保证金299元。（符合退费条件后可退费）

第三步：添加负责人微信，拉入对应的读书会讨论群
（我们也会对每次分享的内容进行录制，剪辑后发布在集智学园官网上，供读书会成员回看）

论文阅读清单

I. 因果涌现理论

  • Cosma Rohilla Shalizi and Cristopher Moore. “What Is a Macrostate? Subjective Observations and Objective Dynamics.” ArXiv:Cond-Mat/0303625, March 29, 2003. http://arxiv.org/abs/cond-mat/0303625.

  • Erik Hoel. “When the Map Is Better Than the Territory.” Entropy 19, no. 5 (April 26, 2017): 188. https://doi.org/10.3390/e19050188

  • E. P. Hoel, L. Albantakis, and G. Tononi. “Quantifying Causal Emergence Shows That Macro Can Beat Micro.” Proceedings of the National Academy of Sciences 110, no. 49 (December 3, 2013): 19790–95. https://doi.org/10.1073/pnas.1314922110.

  • Thomas Varley and Erik Hoel. Emergence as the conversion of information: A unifying theory[J]. https://arxiv.org/pdf/2104.13368.pdf

  • L. Barnett and A. K. Seth. Dynamical independence: discovering emergent macroscopic processes in complex dynamical systems[J]. https://arxiv.org/pdf/2106.06511.pdf

  • Fernando E. Rosas, et al. Reconciling emergences: An information-theoretic approach to identify causal emergence in multivariate data[J]. https://arxiv.org/abs/2004.08220


II. 因果涌现应用

  • Klein, Brennan, and Erik Hoel. “The Emergence of Informative Higher Scales in Complex Networks.” ArXiv:1907.03902 [Physics], January 21, 2020. http://arxiv.org/abs/1907.03902.
  • Klein, Brennan, and Erik Hoel. “Uncertainty and Causal Emergence in Complex Networks.” ArXiv:1907.03902 [Physics], July 8, 2019. http://arxiv.org/abs/1907.03902.
  • Griebenow, Ross, Brennan Klein, and Erik Hoel. “Finding the Right Scale of a Network: Efficient Identification of Causal Emergence through Spectral Clustering.” ArXiv:1908.07565 [Physics], August 20, 2019. http://arxiv.org/abs/1908.07565.
  • Simon Mattsson, Eric J. Michaud, and Erik Hoel. “Examining the Causal Structures of Deep Neural Networks Using Information Theory.” ArXiv:2010.13871 [Cs], October 26, 2020. http://arxiv.org/abs/2010.13871.
  • Hoel, Erik, and Michael Levin. “Emergence of Informative Higher Scales in Biological Systems: A Computational Toolkit for Optimal Prediction and Control.” Communicative & Integrative Biology 13, no. 1 (January 1, 2020): 108–18. https://doi.org/10.1080/19420889.2020.1802914.
  • Chvykov, Pavel, and Erik Hoel. “Causal Geometry.” ArXiv:2010.09390 [Hep-Th, Physics:Physics], October 19, 2020. http://arxiv.org/abs/2010.09390.
  • Bogdan-Eduard-MădălinMursa，LauraDioşan，AncaAndreica：Network motifs: A key variable in the equation of dynamic flow between macro and micro layers in Complex Networks，Knowledge-Based Systems Volume 213, 15 February 2021, 106648


III. 相关

Sloopy models

  • Sloopy Model: https://www.lassp.cornell.edu/sethna/Sloppy/

  • Gutenkunst, Ryan N., Joshua J. Waterfall, Fergal P. Casey, Kevin S. Brown, Christopher R. Myers, and James P. Sethna. “Universally Sloppy Parameter Sensitivities in Systems Biology Models.” PLoS Computational Biology 3, no. 10 (2007): e189. https://doi.org/10.1371/journal.pcbi.0030189.

  • Machta, B. B., R. Chachra, M. K. Transtrum, and J. P. Sethna. “Parameter Space Compression Underlies Emergent Theories and Predictive Models.” Science 342, no. 6158 (November 1, 2013): 604–7. https://arxiv.org/pdf/1303.6738.


Machine Learning and Renormalization

  • Li, Shuo-Hui, and Lei Wang. “Neural Network Renormalization Group.” Physical Review Letters 121, no. 26 (December 26, 2018). https://doi.org/10.1103/PhysRevLett.121.260601.

  • HY Hu, SH Li, L Wang, YZ You Machine learning holographic mapping by neural network renormalization group  – Physical Review Research, 2020. https://journals.aps.org/prresearch/pdf/10.1103/PhysRevResearch.2.023369

  • Hong-Ye Hu, Dian Wu, Yi-Zhuang You, Bruno Olshausen, Yubei Chen: RG-Flow: A hierarchical and explainable flow model based on renormalization group and sparse prior, https://arxiv.org/pdf/2010.00029.pdf

  • Koch-Janusz, M., Ringel, Z. Mutual information, neural networks and the renormalization group. Nature Phys 14, 578–582 (2018). https://www.nature.com/articles/s41567-018-0081-4

  • Shuo-Hui Li : Learning Non-linear Wavelet Transformation via Normalizing Flow, https://arxiv.org/abs/2101.11306


Information theory

  • Tononi, Giulio, Melanie Boly, Marcello Massimini, and Christof Koch. “Integrated Information Theory: From Consciousness to Its Physical Substrate.” Nature Reviews Neuroscience 17, no. 7 (July 2016): 450–61. https://doi.org/10.1038/nrn.2016.44.

  • David Krakauer: The information theory of individuality, https://link.springer.com/article/10.1007/s12064-020-00313-7#Sec10


Others

  • Packard, N. H., J. P. Crutchfield, J. D. Farmer, and R. S. Shaw. “Geometry from a Time Series.” Physical Review Letters 45, no. 9 (September 1, 1980): 712–16. https://doi.org/10.1103/PhysRevLett.45.712.

  • Shalizi, Cosma Rohilla, Kristina Lisa Shalizi, and James P. Crutchfield. “An Algorithm for Pattern Discovery in Time Series.” ArXiv:Cs/0210025, November 26, 2002. http://arxiv.org/abs/cs/0210025.


Defining of Emergence

  • Kim J. Emergence: Core ideas and issues[J]. Synthese, 2006, 151(3): 547-559.

  • Kivelson S, Kivelson S A. Defining emergence in physics[J]. NPJ Quantum Materials, 2016, 1(1): 1-2.

  • Bonabeau E. Predicting the unpredictable[J]. Harvard Business Review, 2002, 80(3): 109-116.


Use of emergence

  • Holman P. Engaging emergence: Turning upheaval into opportunity[M]. Berrett-Koehler Publishers, 2010.


IV. 自指

  • Naoto Kataoka and Kunihiko Kaneko. Functional Dynamics. I: Articulation Process[J]. Physica D: Nonlinear Phenomena, 2000,138(3-4): 225–50. https://doi.org/10.1016/S0167-2789(99)00230-4.
  • Naoto Kataoka and Kunihiko Kaneko. Functional Dynamics: II: Syntactic Structure[J]. Physica D: Nonlinear Phenomena, 2001,149(3): 174–196. https://doi.org/10.1016/S0167-2789(00)00203-7.
  • Walker, S. I., Cisneros, L., and Davies, P. C. W.. Evolutionary Transitions and Top-Down Causation[A]. Proceedings of the ALIFE 2012: The Thirteenth International Conference on the Synthesis and Simulation of Living Systems[C]. East Lansing, Michigan: ASME, 2012, 283-290. https://doi.org/10.1162/978-0-262-31050-5-ch038
  • Theodore P. Pavlic, Alyssa M. Adams, Paul C. W. Davies, et al. Self-referencing cellular automata: A model of the evolution of information control in biological systems[J]. 2014. https://arxiv.org/pdf/1405.4070.pdf
  • Nomura T. Formal description of autopoiesis for analytic models of life and social systems[C]//Proc. 8th Int. Conf. Artificial Life (ALIFE VIII). 2002: 15-18. https://dl.acm.org/doi/10.5555/860295.860299
  • Hofmeyr J H S. A biochemically-realisable relational model of the self-manufacturing cell[J]. Biosystems, 2021: 104463.
  • Letelier, J. C., Marı́n, G., & Mpodozis, J. (2003). Autopoietic and (M,R) systems. Journal of Theoretical Biology, 222(2), 261–272. doi:10.1016/s0022-5193(03)00034-1
  • Gánti T. Chemoton theory: theory of living systems[M]. Springer Science & Business Media, 2003.


（论文阅读清单可上下滑动查看）




详情请见：

因果涌现读书会启动：连接因果、涌现与自指——跨尺度动力学与因果规律的探索



推荐阅读



点击“阅读原文”，可报名读书会