论文题目：

Characterizing cycle structurein complex networks

论文地址：

https://www.nature.com/articles/s42005-021-00781-3

1. 什么是圈？它凭什么重要？

圈（cycle/loop）在我们的生活和网络中无处不在，它和链路（chain）、星（star）结构等一起作为网络的基本构成要件，在复杂网络中扮演着非常重要的角色。

一个圈，简而言之，就是一个由相同起点和终点构成的封闭路径。节点对之间的交互是简单的，但当它们构成环路时，便有了形成超越线性交互过程的结构基础。三角形是最小的圈，从二到三，在数量上只增加一，但却带来了质的变化。如果分别检索包含“二”和“三”的成语，就会发现前者更多是静态的描述性词汇，而后者更多指代包含复杂交互细节的行为或故事（图1）。

图1 包含“二”和“三”的常用成语举例

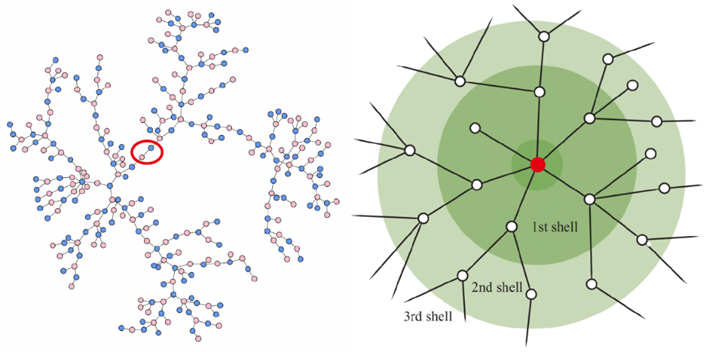
如果一个网络中没有圈结构，这个网络就会退化成树形网络，这时如果只移除网络中的一条连边或者一个节点，都会导致网络至少分裂成两个分支（图2左），甚至直接破碎成无数碎片，并导致其功能的必然崩溃（图2右）。而如果两个节点在一个圈中，即使圈上的某个节点（或连边）被移除，它们的连通性仍然不会被破坏。可见，不同于链路与星结构，圈为其上的节点带来了冗余的路径，这使得网络的连通性被大大增强，变得更加鲁棒。

另一个更重要的方面——就网络的功能和动力学而言，圈是反馈效应的结构基础，也是对反馈过程本身的逻辑描述。圈的存在使得节点能够从邻域捕获自己先前行为产生的影响，或者网络能够感知输出效果，从而据此调整接下来的行为。“用进废退”、“多退少补”、“有则改之，无则加勉”等成语也包含这样的反馈过程。反馈效应是网络结构和功能演化的重要机制，是网络复杂性的重要源头和形成智能的必要条件，也是协同效应、自组织涌现等复杂行为和现象的基础。更广泛地，反馈过程是人与外在环境时时刻刻交互的逻辑写照，也广泛存在于化学反应、控制系统、生态平衡和社会经济之中（图3）。因此，对圈结构的深入研究可以为优化网络连通性和抗攻击能力、快速调整网络状态以及最大化传播效果等提供新的洞见和方法。

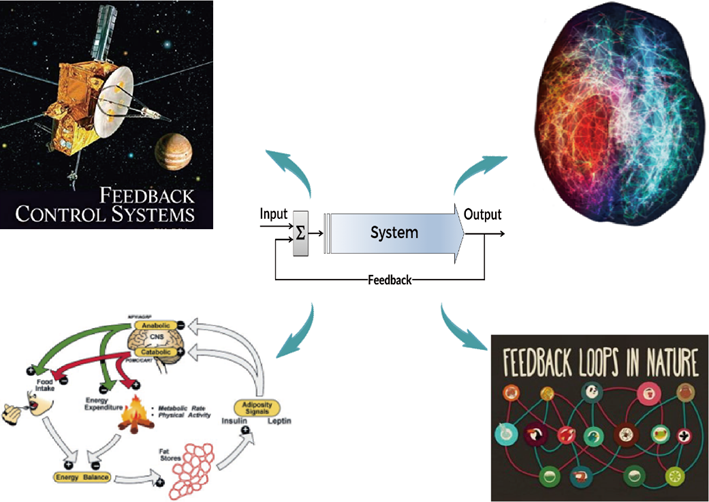
图3 以反馈效应为基础的各种复杂系统

2. 有哪些研究进展？

近期的研究发现，以圈结构为基础设计的网络具有最优的同步能力（全齐性网络）[1]和控制鲁棒性[2]（图4上）；而人脑中两种高阶圈结构，团（clique）和洞（cavity），前者作为信息处理和记忆的单元，后者作为跨脑区信息整合和分发的功能基础，对于人脑的并行处理与高级认知活动至关重要[3]（图4下）。此外，圈结构也被用于刻画网络局部的节点聚集程度[4–7]，测量网络与树形网络之间的近似程度[7,8]，预测好友关系的出现[9]和未被观察到的蛋白质交互作用[10]等。

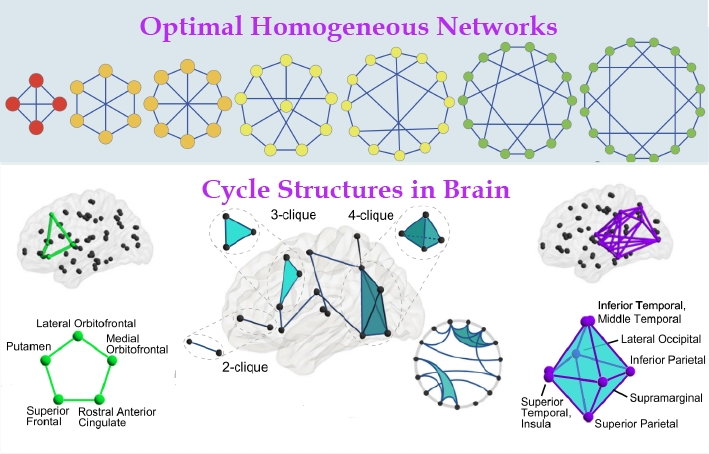
图4 圈结构在最优同步网络和人脑中的典型结构示例

然而相对于链结构和星结构，圈结构的相关研究仍然远远不足。首要的原因是圈的检索和计算并非易事。随着圈长度的增加，其数量成指数倍增加，计算复杂度和时间代价很高，且这个问题至今也是进行圈相关研究时所要面对的基本问题。其次，由于小世界网络与无标度网络的研究持续火热，吸引了科研群体的大量关注。在一定程度上，可以认为小世界网络与无标度网络的研究本质是对链结构与星结构特性的探索。故而收链、星于东隅，而失圈于桑榆。

可见，圈结构具有普遍的存在性和重要性，然而却少有人将它作为一般性的网络统计指标或普适性任务的工具，用于网络研究之中，比如，网络中的重要节点识别。虽然聚集系数所考虑的三角形就是最小圈，但因其与节点度的负相关性，所以并不能用于一般的重要节点识别任务[11]。

3. 本研究主要内容

就在上周，范天龙等人在期刊Communications Physics上发表了题为《Characterizing Cycle Structure in Complex Networks》的研究成果。作者基于对圈结构的统计特征分析，提出了一个新的矩阵，圈数矩阵（cyclenumber matrix），用于表征网络中的圈信息，并基于此，提出了一个新的节点重要性排序指标，圈比（cycle ratio）。通过与现有指标进行对比，作者发现圈比所识别出的重要节点与原有的多个重要节点排序指标的结果非常不同，而原有的多个指标的结果却是非常相似的。进一步的实验表明，使用圈比所识别出的重要节点对网络进行恶意攻击，会使得网络更快地崩溃；或者通过牵制控制这些节点，可以使网络更快地达到同步状态；而在传播能力方面——无论在快速传播还是完全传播中，这些节点也具有最大的传播能力。这些结果表明，对圈结构的深入研究，很可能为网络科学提供新的洞见、指标、模型和算法，并对提升网络抗攻击能力、优化控制系统设计、增强新冠病毒防控效力、以及最大化网络营销等带来新的启发。

所谓圈比，顾名思义，即是指一个节点参与到其他节点的最短圈的程度。这里的最短圈是指包含这个节点的长度最小的圈。图5展示了圈数矩阵和圈比的计算过程。

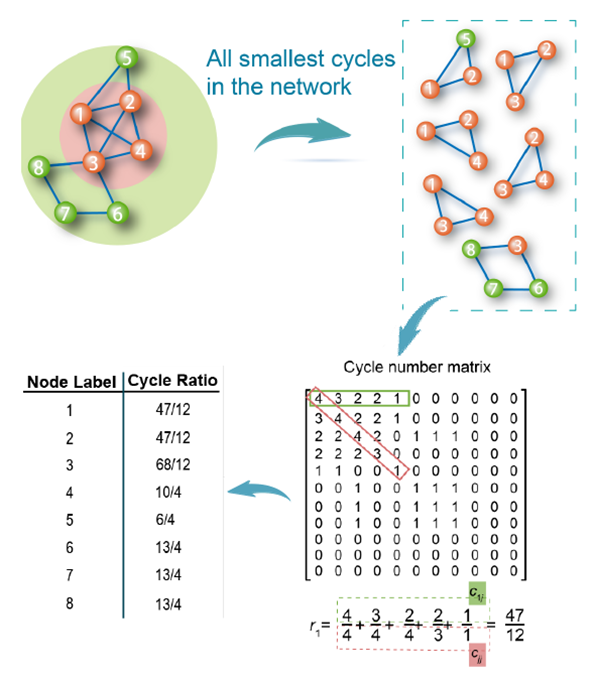
注意到，在以往的节点中心性指标的定义中，往往从目标节点自身的视角出发，看邻居节点对我的贡献，而在圈比中，这一点反了过来。这不仅仅是换了一个新的特征来识别重要节点，而是换了一个新的思路，即一个节点是否重要，取决于它对邻居的结构和动力学过程的参与程度——我的价值并非取决于以自我为中心看邻居们对我的利用价值有几何，而是看我对邻居们做了多少贡献。如果我对社会（圈上的邻居节点）的贡献越大，承担的社会角色（包含我的圈的数量）越多，则我越重要。可以说，这背后隐含着价值观或哲学视角的转换。

助人者自助，重人者自重。大我无我，而寓以万物。

另外需要注意的一点是，这里只用了节点的最短圈来计算圈数矩阵和节点的圈比。为什么不考虑更长的圈呢？文章分析结果表明，考虑更长的圈并不能提高圈比识别重要节点的准确性，反而会使其下降。这是因为对于节点的结构和动力学而言，局部结构往往扮演着更重要的角色，圈越长，则其上节点的相互影响越弱，且因测量范围重叠也会使指标的区分能力下降。

作者比较了新指标与原有指标之间的相关性，结果如图6所示，可以看出原有的三种指标之间相关性很高（平均0.9），而圈比与他们却相对较低（平均0.6）。这说明从圈结构的视角，圈比发现了更多已知指标所不能提供的新信息——这一点非常重要，但很容易被忽视，因为这暗示着新指标的潜在价值。而在蛋白质网络（Yeast网络）上的可视化结果，更加直观地反映了它们的差异，如图7所示，前三种指标所选出的重要节点紧密地彼此连接，聚集在一个特定区域，表现出明显的富人俱乐部（rich-club）现象[12]；相反，圈比所识别出的重要节点则广泛地散布在整个网络中，且彼此之间的连接较为稀疏。这是圈比的一个显著优势，因为如果需要找到一组重要节点时，前三种指标选出的重要节点因为紧密聚集而使得其影响范围高度重叠，因此集体影响力可能较弱。而圈比则不会。

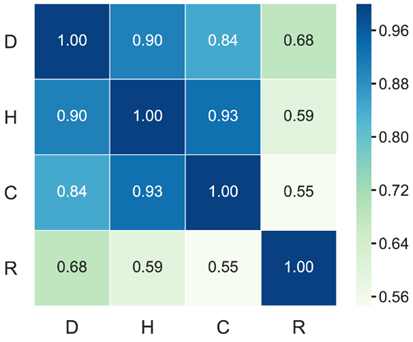
图6 平均相关性矩阵，颜色越深表示相应两种指标的相关性越高。这里的D，H，C和R分别表示degree，H-index，coreness和cycle ratio。

进一步的实验表明，圈比所识别的节点在维持网络连通性、促进网络同步和最大化传播方面整体上优于原有指标。这些结果证明圈比在不同的动力学特性上都具有普遍的性能优势。

具体来说，在网络攻击中，按照每个指标的排序结果依次删除节点，并记录每次的剩余网络中的最大连通片的规模，将其累加值作为攻击效果的评判标准[13]。这个值越小，则攻击效果越好，说明该指标所识别的节点对网络的连通性越重要，结果如图8所示。可以看出，圈比可以让网络更快地破碎。

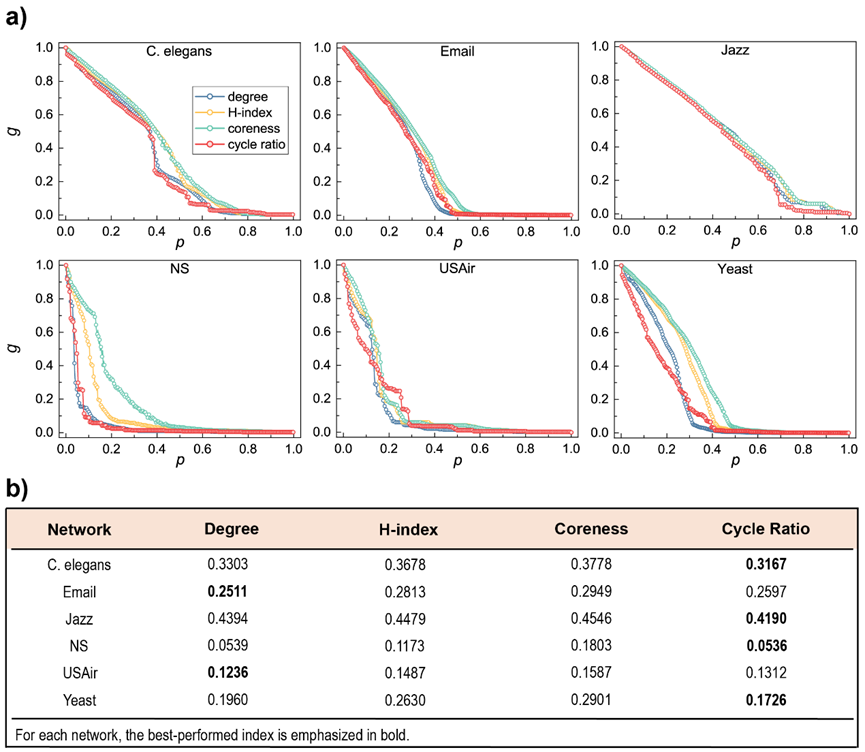
在牵制控制实验中，按照每个指标的排序结果依次对每个节点实施牵制以使其达到理想的状态，并最终使得所有节点状态达到同步。为了测量不同牵制控制策略的效果，作者提出了一个新的测量方法，牵制有效性指标（pinning efficiency index）。它使用主子矩阵的最小非零特征值的倒数来刻画被牵制网络的同步能力[14]，这个值越小，则该牵制控制策略越有效。这里的主子矩阵是通过删除网络的拉普拉斯矩阵中被牵制节点对应的行和列后捕获的。结果如图9所示，显然，圈比所识别的节点具有最好的牵制控制效果。

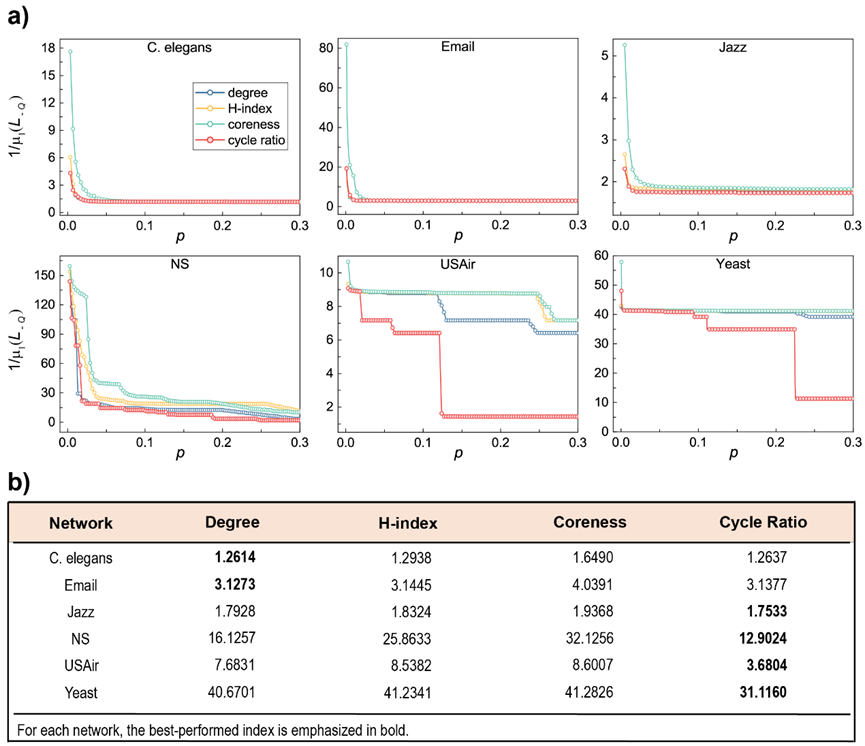
最后的传播实验，作者着重考察了圈比的快速传播能力。相比于常见的完全传播（传播过程达到收敛），人们更感兴趣的是哪些节点可以在尽可能短的时间内传播范围更广，例如市场营销、在线信息扩散，它们往往具有很强的时效性。而在传染性疾病防控中，最关键的问题是在疾病暴发早期能够对高传播性节点进行控制或免疫，如我们国家当下正采取的新冠肺炎的“动态清零”防控策略。作者用SIR传播模型（susceptible-infected-recovered model）[15]来仿真一组节点的传播能力，即将被选中的这组节点初始化为感染状态而其余节点为易感状态，然后进行传播实验，并记录每一步的感染数量，感染数量越多，则这组节点的传播能力越强。结果如图10所示，显然圈比所识别的节点的传播能力是最好的。此外，作者也比较了完全传播情况下圈比与另一个全局性指标coreness的性能，结果仍然是圈比的优势明显。

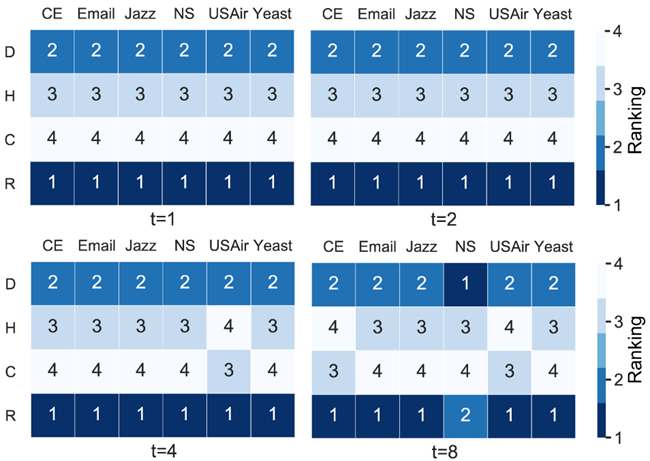
除了上文提及的指标外，作者也全面比较了圈比与聚集系数（clustering coefficient）、特征向量中心性（eigenvectorcentrality）指标的性能，与以上结论并无二致。

作为重要节点识别方法，圈比有多种现实意义。比如对于电力网络、航空运输网络、金融网络和互联网等，对其中的重要节点实施重点保护，可以更有效地增强它们抵御恶意攻击中的能力，从而维持其功能的正常运转。反之，对于恐怖分子网络等有害目标，则可以获得更有效地打击以使其更快崩溃。而且这种打击往往并不需要在物质层面实施，只需要破坏甚至干扰它们的信息系统即可。另外，圈比在牵制控制方面的优异性能，可以用于解决多智能体系统的一致性问题，并优化无人机集群和移动传感网络等系统的协同控制。

作者也发现圈数矩阵与超网络之间的关系。如果将超边视为圈，超网络的关联矩阵乘以它的转置矩阵后，也可以得到圈数矩阵，这时对角元素表示超边数，非对角元素表示两个元素共有的超边数。因此，我们可以将圈比的概念推广到超网络上，用一个节点参与到其他节点的超边的程度之和来量化超网络中的节点重要性。

除了最短圈，其他更长的圈和更高阶的圈，如团和洞，也在网络结构和功能中扮演了重要角色，对于他们的研究也需要新的方法。谱分析和代数拓扑[16,17]等方法因其自身在高阶分析方面的优势，在未来的研究中或可发挥重要作用。

最后——但却同样重要的问题，是模型网络与实证网络的圈分布和圈的程度存在巨大差异。所以以往用模型网络或随机网络（如不同阶的零模型网络）上的动力学仿真结果作为实证网络的性能基准的研究方法，存在诸多值得探讨之处，还需要对此进一步研究。或许深入研究网络中圈是如何形成的，可以揭示出新的网络演化机制。

相关研究 

• Searchingfor Optimal Network Topology with Best Possible Synchronizability

• Totallyhomogeneous networks

• Computingcliques and cavities in networks

集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅：

点击“阅读原文”，追踪复杂科学顶刊论文