导语


物理系统在对称与对称性破缺之间，平衡与非平衡之间，互易与非互易之间，仿佛交织着一首二重奏鸣曲，导致种种奇妙的物态涌现和相变。这些物理系统的非互易性作用和相变，能否推广到更复杂的宏观系统，比如生物的集群现象、神经元网络的同步、斑图形成？近期发表在 Nature 上的论文“Non-reciprocal phase transitions”基于序参量场论方法，结合分岔理论的奇异点研究，捕捉到了三种典型的远离平衡态的自组织非互易性：同步化、结群和斑图形成；并区分了手征相、交换相与混合相三种物相，为这一大类非互易临界现象的一般理论奠定了基础。


研究领域：非平衡系统，非互易性，对称性破缺，临界相变，活性物质，集体运动

十三维 | 作者

梁金 | 审校

邓一雪 | 编辑



论文题目：

Non-reciprocal phase transitions

论文链接：
https://www.nature.com/articles/s41586-021-03375-9


目录

一、非互易作用与对称性破缺

二、非互易性的序参量描述

三、运动模式：结群、同步化与斑图形成

四、非互易相变：手征相、交换相与混合相

五、识别并分析非互易系统奇异点

六、总结：观测量、守恒流、非互易性、对称性破缺与相变


在随时间演化而变化的非平衡态下，系统间的互易性（reciprocity）缺失是一种常态而非例外。非互易性发生在活性物质、神经网络、兼具顺从和叛逆成员的社会群体、定向界面生长现象和超材料等非平衡系统中。尽管之前对非互易介质中波的传播有了一定深入研究，例如光学系统在「宇称-时间」（PT）对称变换下的破缺[1-20]，但人们对非互易作用中多体系统的集体行为影响依然所知甚少。
 
近期发表在 Nature 上的论文 Non-reciprocal phase transitions，基于序参量场论方法描述了这些远离平衡态相的涌现，并捕捉到了三种典型的自组织非互易性：同步化、结群和斑图形成。作者研究发现，非互易性会导致一种自发连续性对称破缺动态恢复的时间依赖性手征相，一种丧失时间平移不变性而保持离散对称性的交换相，以及二者的混合相。作者通过简单的机器人演示和多种数值模拟来说明这些机制。这种非互易相变是被称为奇异点[21]的光谱控制的，系统中的集群现象包括从活性时间（准）晶体到奇异点强化下斑图形成和滞后（hysteresis）等等。这些工作为非平衡态系统下动力过程不受优化原则制约的临界现象一般理论奠定了基础。
 
 



一、非互易作用与对称性破缺




物体运动状态或系统之间总具有某种作用关系。例如平衡系统下的牛顿第三定律，其作用力与反作用力——如地球和月球之间的万有引力，总是大小相等、方向相反，即 FAB = -FBA。但让我们考虑这样一种情况。据说有一次物理会议后，爱因斯坦和居里夫人等人爬到了阿尔卑斯山顶。居里夫人问，现在地球的质心发生了变化，那么月球怎么能那么快知道我们在爬山，并改变对地球的引力大小呢？由相对论，任何已知作用和信号的传递速度都不得超过光速，因此虽然最后地月之间处于平衡态，但一定存在某些时刻使得 FAB ≠ -FBA ，即中间产生了非互易性作用。
 
但如果从更基本的守恒角度来看，地月之间的引力依然遵守着某种不变性。只需假定传播介质具有动量，那么整个系统仍然在一切时间内都严格保持动量守恒：即相互作用的所有物体的运动总趋势（mv）在一切空间不变。动量守恒是空间均匀性（扭曲程度）的体现，它意味着物体运动规律在所有空间成立，无论任何地点和观察者（参照系）。可见它非常根本，是科学规律产生的大前提。
 
动量守恒还可以数学群论语言来表达：空间具有平移对称性——对物体进行「空间平移」操作（变换）后，物体运动趋势以及相关物理规律不变。20 世纪最伟大的数学家之一诺特，她证明了理论物理学的中心结果诺特定理（Noether’s theorem）[22]：每种连续的对称性都对应着一种守恒律。
 

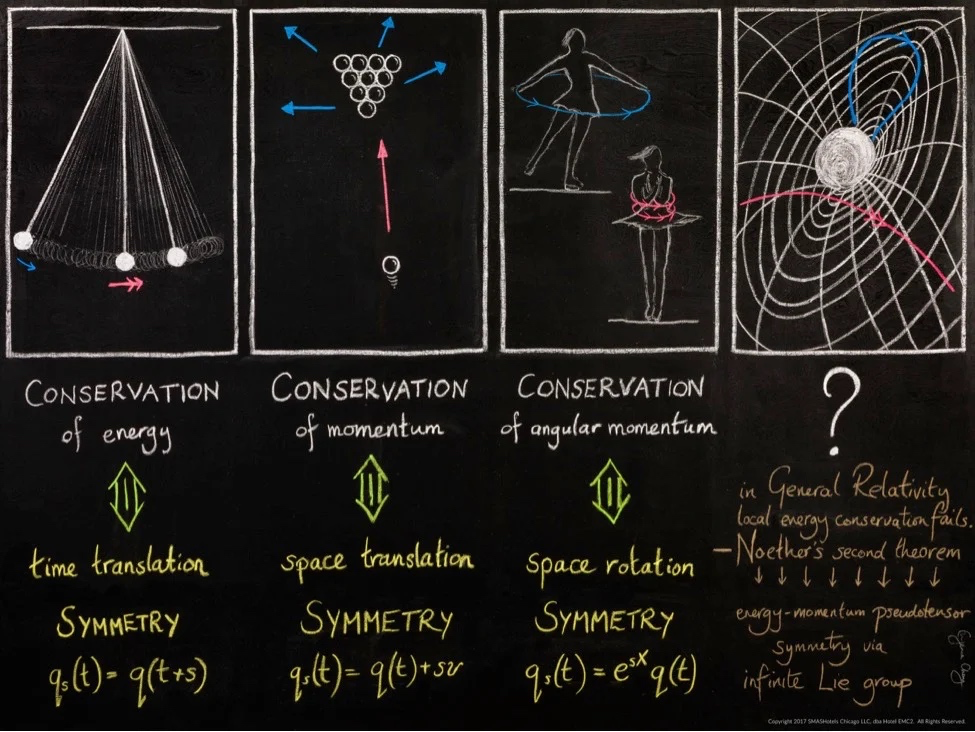
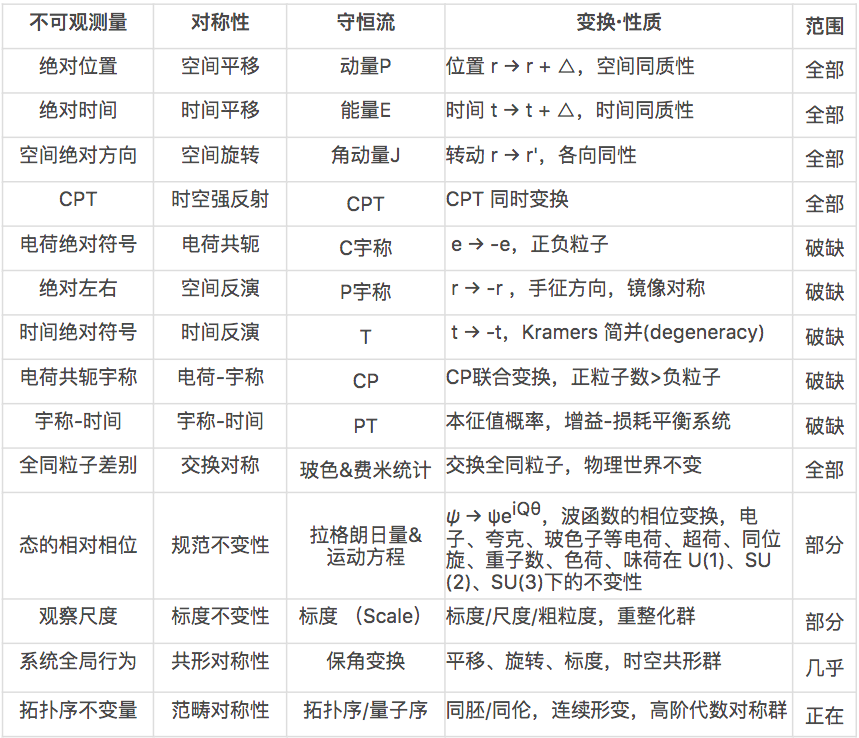
图1：诺特定理下对称性与守恒量之间存在对应关系[23]，包括动量-空间平移对称，角动量-空间旋转对称、能量-时间平移对称等等。

 
对称性意味着规律的普适性，它不仅表现为时空结构，还以运动方程形式体现在物体运动和相互作用系统中。从作用角度看即存在互易性关系：reciprocal 在拉丁语词源就是「向前和向后走的路一样」的意思[40] 。相反，非互易性的存在则意味着出现了某种情况下的守恒破坏和 对称性破缺。
 
由于华裔科学家杨振宁和李政道获得 1957 年诺贝物理学奖，一个比较知名的守恒破坏是宇称不守恒（Parity violation）：在弱相互作用下，互为镜像的粒子运动不对称，K介子自旋在不同手征（chiral）方向磁场中发生了不同的衰变。这种微观下的非互易性，与宏观世界镜像必然对称相比是一个巨大的反常识。
 
不过，就像前面引力的故事一样，在量子力学在复数域的推广中，又有一类「宇称-时间」对称性（Parity-Time，PT）：粒子或系统在空间镜像和时间反演变换下的不变性。对一个与外界无能量交换的保守系统（动能和势能之和为定值）来说，其哈密顿量共轭不变且具有实数特征值。同样还有PT对称性破缺，对一个有能量流入与流出的非平衡开放系统（增益-损耗系统），会伴随着复数特征值出现，此时PT不再守恒，且在相变过程中会出现奇异点（exceptional points）。
 
物理系统某个对称被破坏后往往可以通过另一个对称来弥补，这两个对称的乘积依然守恒。除了PT对称性外，还有CP对称及破缺等等。对粒子系统而言，只有加上电荷的CPT联合对称变换才是适合所有范围守恒的。
 
图2：增益-损耗系统的PT对称性和破缺[24]
 
可见所有物理系统，无论全局还是局域、连续还是离散，在守恒与不守恒，对称与对称性破缺，平衡与非平衡之间，互易与非互易之间，仿佛总是交织着一首二重奏鸣曲，导致种种奇妙的物态涌现和系统相变。互易性与非互易性一起出现在物理学的所有分支中，从力学、热力学、凝聚态物理、电磁学和光学、相对论、量子力学、粒子和纳米物理学到宇宙学中，支撑着世界无数的现象和应用。
 
那么问题来了：这些物理系统的非互易性作用和相变，能否推广到更复杂的宏观世界中去？
 
最近 Non-reciprocal phase transitions 的研究工作，通过序参量的场论方法，结合分岔理论的奇异点研究，捕捉到了三种典型的远离平衡态的自组织非互易性：结群、同步化与斑图形成，并区分了手征相、交换相与混合相三种一般物相，为这一大类非互易临界现象的一般理论奠定了基础。
 

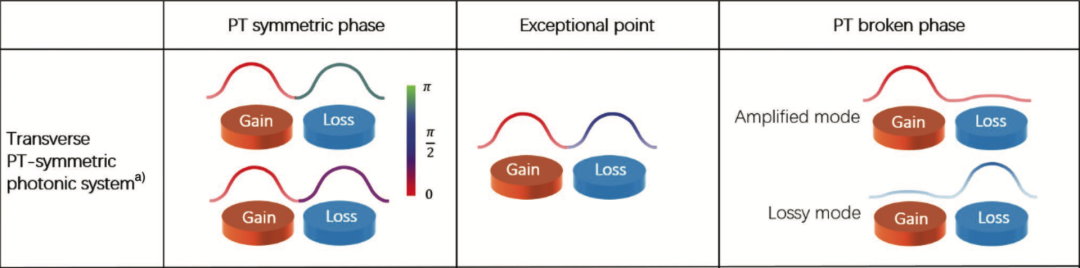
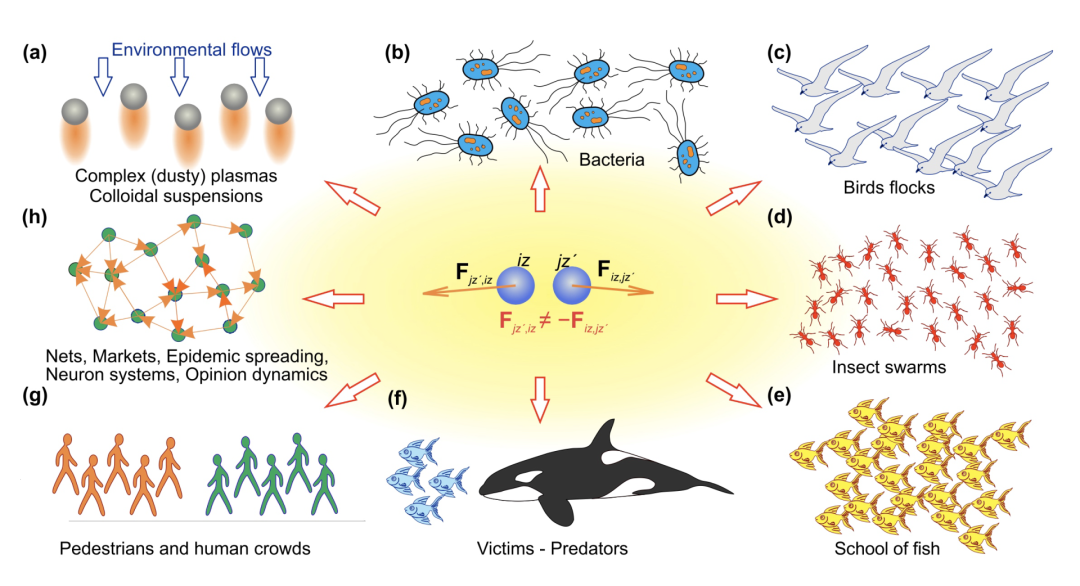
图3：打破牛顿第三定律的「非互易世界」：(a) 环境流中复杂等离子体和胶体悬浮液 (b) 菌群 (c) 鸟群 (d) 昆虫群 (e) 鱼群 (f) 各种捕食者—食饵系统 (g) 行人和人群 (h) 网络、金融市场、流行病传播、神经系统、舆情动态等[25]

 
 



二、非互易性的序参量描述




序参量（order parameter）是一种刻画物理系统相变过程中有序化程度和对称性的指标（标量或矢量）。在连续相变中，它主要度量相变点从零（无序）到非零（有序）之间的变化，数值（模）越大，则系统有序度越高，对称性越差。协同性提出者赫尔曼·哈肯（Hermann Haken）说：
序参量就像一个木偶戏的牵线人，他让木偶们跳起舞来，而木偶们反过来也对它起影响、制约着它[26]。
 
例如在晶格中，最重要的变量是原子远离晶格位置的运动，磁体中则是忽略大量细节后电子间复杂相互作用导致的局部磁化方向。它们都可以用序参量来表示：对空间每个点 x=(x,y,z)，都有一个局部运动或磁化 M(x) 的方向，标明打破向某个方向的对称性。这种从真实空间到序参量空间的映射就构成了序参量场：它把磁体中不同点带到一个包含大小和方向的二维球体表面上。
 
图4：从真实空间的点到序参量空间的运动矢量[27]
 
在非互易性作用中由于系统随时间在演化，故对物种群或场中的每个物种 a，可以用序参量向量 va(t,x) 来模拟：即 a 在时间 t 位置 x 的矢量。那么考虑两个主体 a、b，很容易得到两个序参量关系在时间下的导数：
 
 
其中 Aab 和 Bba 分别是 a → b，和 b → a 的耦合参数矩阵，代表对对方的影响强度，O(∇) 则是被省略的非线性空间导数项。那么考虑一个一般的多体系统（如四体），即可得到表示动力系统序参量演化的一般方程：
 
 
方程（1）表示序参量 va 在 b、c、d 影响下随时间的变化率：它与 vb 、Aab， vb、vc、vd 和 a 与 bcd 的耦合参数矩阵 Babcd 都有关（这里隐式对多体间作用进行了合并）。
 
由于向量 va(t,x) 包含了方向和大小，故在二者有不同改变时，会形成不同的相变模式：方向改变时形成结群（flocking），周期性运动导致同步化（synchronization），纯粹做空间平移运动则是斑图形成（pattern formation）。
 
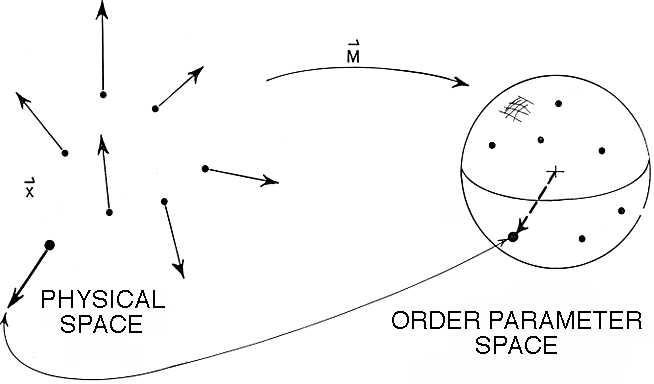
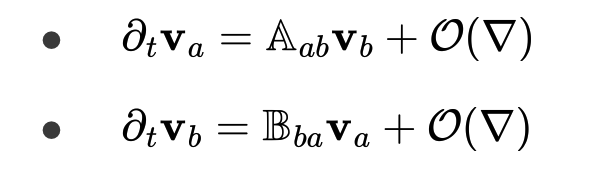
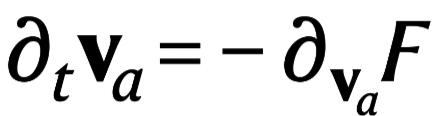对平衡系统相变，由于对能量（自由能） F 有 ，多体之间的耦合系数完全对称；故这里只要允许  Aab ≠ Bba，即可将互易系统的临界现象[28]理论扩展到结群、同步化和斑图形成在内各种形式的非互易系统，包括诸如编码自推进粒子的平均速度、耦合振荡器的平均相位或周期图案的振幅和位置等等。
 
对于其中的同步化过程，作者通过编程为非互易作用的同步机器人进行了实验。种群中有蓝红两种机器人AB，同种为互易作用，对各自的耦合参数则 JAB ≠ JBA：当 JAB>0 时，蓝色试图与红色对齐（同向），JAB<0 时，则试图反对齐（antialign）。实验前这些机器人按照直列（Alignment）或反直列对齐。
 
图5：非互易旋转的机器人
 

实验开始，这些机器人即按照初始参数，没有任何外部调节下自发地顺时针或逆时针旋转，打破了一开始的宇称对称性。即伴随序参量 vA 和 vB 从0到非零的变化，机器人群呈现出了从静态直列到宇称自发破缺的手征运动相，并在稳定下来后使序参量重新趋于零。详见下面视频：



正如第一节图2、图3所示，编程机器人的运动过程非常类似增益-损耗系统和打破PT对称性的非平衡相变，它们在本质上是同一类非互易系统相变。但在运动表现模式上又有所不同，具体而言对应着不同对称性的打破。
 

 



三、运动模式：

结群、同步化与班图形成




诺特定理表明，每一种连续对称性都代表一种守恒量，相应的破缺则让其不再守恒。对方程（1）而言，由于序参量矢量 va(t,x) 包含了方向和大小，因此可以代表主体之间方向和位移可能同时改变的旋转运动、没有位移在时间内的周期运动以及纯粹在空间中的平移运动。
 
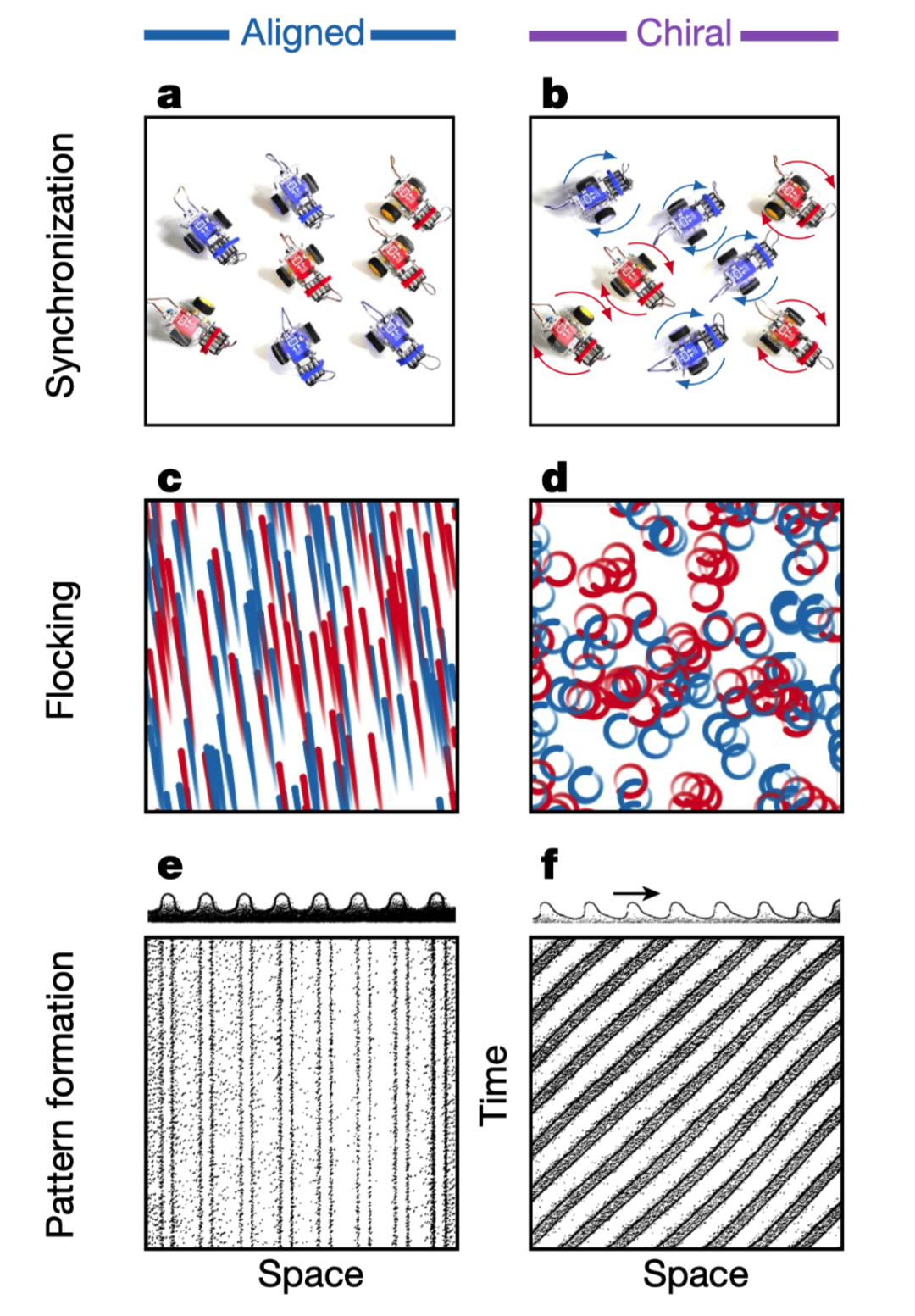
  • 旋转形成通过互相绕圈接近的结群（flocking），它源自空间各向同性（isotropy，无法区分绝对方向、无方向特殊的）而保持的旋转不变性，对应角动量守恒定律。
  • 周期运动导致主体之间的同步化（synchronization），它源自时间平移不变性（即物理定律适用于所有时间），对应能量守恒定律。
  • 平移运动则导致斑图形成（pattern formation），它源自空间平移不变性（空间均匀性），对应动量守恒定律。

以上三种模式，与微观粒子类似，都会在跨越奇异点后打破宇称，形成一种自发对称性破缺的手征相。如图6所示：

图6：非互易作用奇异点相变的机制和例子，序参量耦合参数 JAB≠JBA ，导致了从静态直列到自发打破宇称手征运动的相变。(a,b）非互易同步。被编程为非互易自旋的机器人，自发地顺时或逆时针旋转。(c,d）非互易结群。尽管没有外部扭矩，自推进粒子仍绕圈运行。(e,f）非互易斑图形成。在油-气界面上观察黏性指进（viscous fingering）[15] 实验的一维斑图移动。
 
视频1：非互易结群的分子动力学模拟。底部是自推进粒子各个方向平均的瞬时序参量。
 
 



四、非互易相变：

手征相、交换相与混合相




1. 自发对称性破缺与宏观手征相
 
这些宏观非互易作用下宇称自发破缺的手征相是如何形成的？
 
自发对称性破缺（spontaneous symmetry breaking），和显性对称性破缺（explicitly）不同，它的运动方程和基态保持不变，是系统在时空背景（真空）实际运行时由于存在多个最低能量态（方程的解）而打破了不变性发生相变。自发对称性破缺最初来自固体物理中的超导电性，后被粒子物理用来解释规范玻色子如何获得质量。
 
根据杨-米尔斯理论（Yang–Mills theory），满足局域规范不变性（Gauge invariance）[39]的W玻色子、Z玻色子应当与光子、胶子一样质量为零，但实际测量却并非如此。为此物理学家提出著名的希格斯机制（Higgs mechanism）：存在一种弥漫全空间的量子场即希格斯场，在弱相互作用下会与规范场作用，导致自发对称性破缺，使规范介子产生一种纵向低能态的自由度，并使得 W-、W+和Z三种玻色子获得质量。
 
这个过程被称为 Goldstone 模式（Goldstone mode），它的势函数被形象地表示为一个「草帽图」：
 
图7：Goldstone 模式的自发对称性破缺[41]。原本处在阔边草帽圆顶、保持对称性的球，会不断地被噪声踢向底部一种纵向自由度的低能激发态，从而打破原有的整体对称性。不过在非互易系统中，自发对称性破缺过程还受到横向红色方向做功与路径有关的非保守力作用。
 
在理解了自发对称性破缺和 Goldstone 模式后，让我们考虑两个宇称未显性破缺的主体 A 和 B。对耦合参数JAB 和 JBA，令：


则J+和J-分别代表刻画非互易性作用程度的两个分量。对互易作用（J+=0或J-=0时），序参量 vA 和 vB 会处在同向或反向的两个静态阶段（图8g上左右）。但当非互易作用（JAB≠JBA）且使J+不断增大时，vA 和 vB 就会呈一个固定夹角的恒定角速度 ΩSS 顺或逆时针旋转。即在两个 Ωss=0 的静态相之间，涌现出了一种类似铁磁变化的时间依赖性的非平衡手征相，如图8g上红蓝箭头所示：
 
图8：非互易相变下，奇异点（红点）分岔的手征相自发对称性破缺与两种作用模式。这种非互易「直列-手征」相变过程，同样被看作是PT自发对称性破坏的表现。
 
如图 8h 所示，手征相是由阻尼模式（damped mode，横向非保守力）和 Goldstone 模式这两种过程在某个奇异点凝聚发生的（纵轴为序参量增长率 σ）：

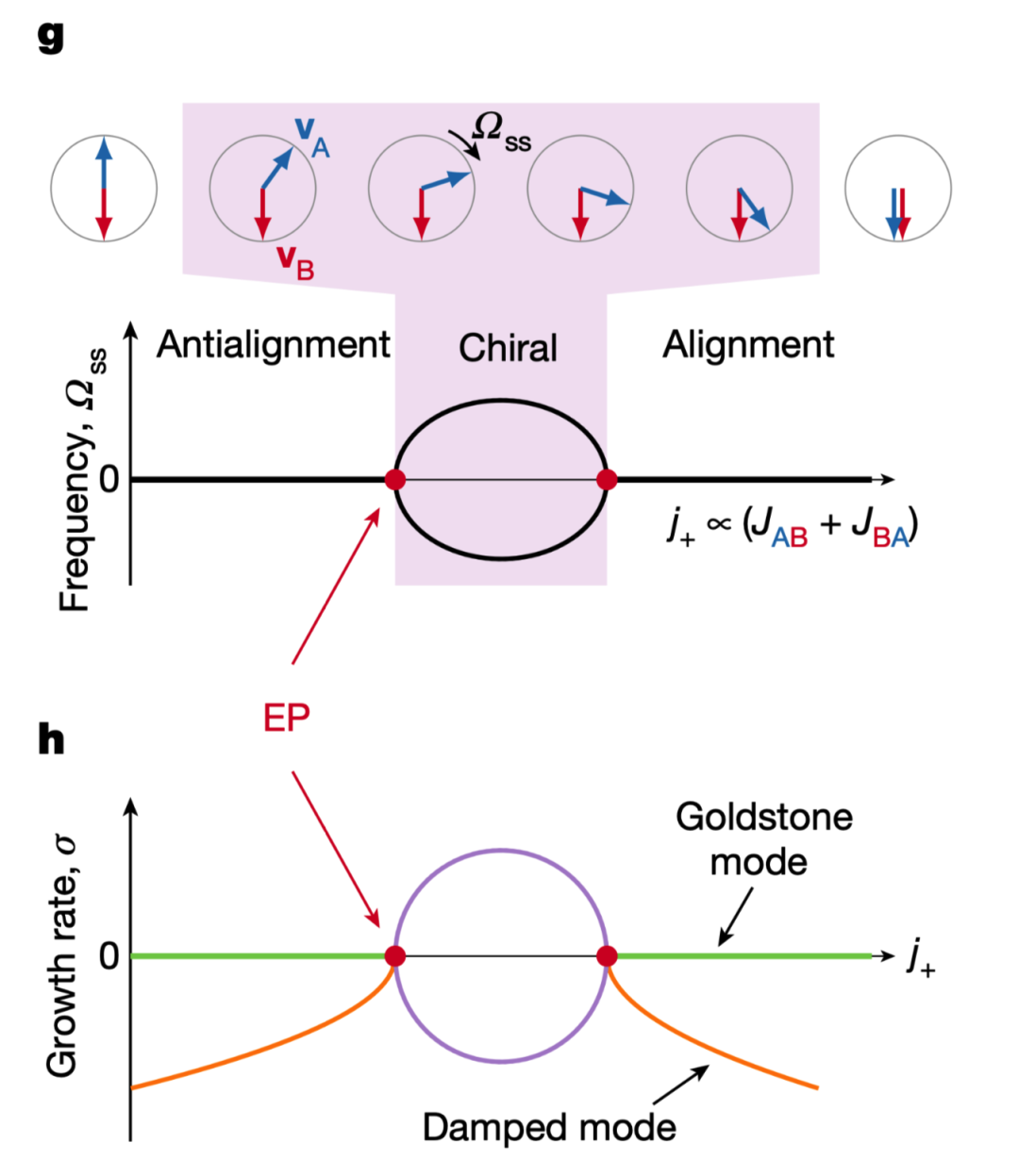
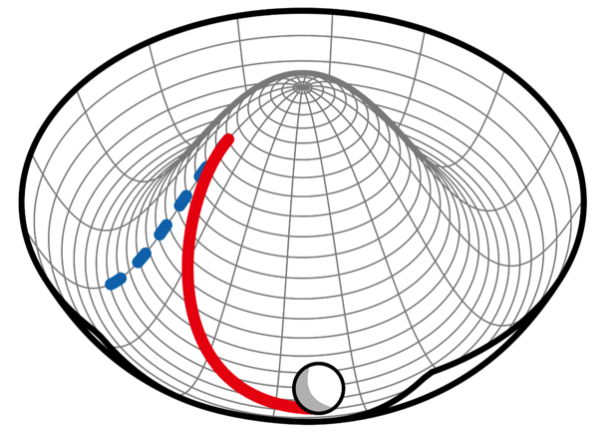
  • 在阻尼模式（橙色），σ < 0，主体因摩擦等介质阻力过大而静止，但阻力随着 J+ 增大而减小；

  • 在 Goldstone 模式（绿色），系统倾向自发对称性破缺的低能稳定激发态，并试图恢复其已破缺的对称性。但当阻尼模式阻力过大， σ=0（球倾向于、但不会掉下去）；

  • 随着J+增加，阻尼减少，当 σ 趋于零时两种模式凝聚成奇异点，此后 Goldstone 模式主导，系统因噪声自发对称性破缺而进入手征阶段（紫色）。且 σ 在最后一个奇异点后重新为0。

 
手征相是由目标相反的主体运动相挫引起的：主体 A 想与主体 B 对齐，但反之不然，这就导致了互相追逃的序参量 vA 和 vB。用编程的红蓝机器人例子来说，除非正好 JAB = -JBA，彼此最终才会追上对方对齐。但由于自然运动中存在不可避免的频率紊乱或噪声（类似于真空作用），又会不断重置激活许多A/B对的运动，使得彼此交互下的手征相变得与宏观现象相关。即系统最终稳态手征相取决于运动噪声和多体效应之间的微妙相互作用。作者经过实验验证，随着主体数增大，序参量标准差降低，即手征相会变得更稳定。
 
手征相可以看作是一种连续对称性自发破缺的动态恢复：Goldstone 模式被噪声所驱动，在相变后，系统则沿着退化基态的流形运行。除了图 4a–f 例子外，手征相还发生在液晶凝固[29]、层状共晶生长[30]、溢流喷泉[31]等自然现象中。
 
2. 时间晶体、交换相与混合相
 
除手征相外，论文作者还发现了一种「交换相」（swap phase，图9b、c绿色区域、9e）：vA 和 vB 沿一个固定方向周期振荡；以及一种「手征-交换混合相」（mixed chiral+swap phase，图9b、c深绿区域），其中交换和手征运动同时发生。
 
图9：不同耦合参数J+和J-下，非互易结群的手征、交换、混合相分布
 
交换相通过丧失时间平移不变性而保持了离散对称性，这和活性（准）时间晶体（active time (quasi) crystal） [32,33] 的特性非常类似。
 
晶体是有序的物质态，其内部的原子或分子按照规则的空间结构排列。晶体形成就是空间平移的自发对称性破缺：例如在水凝结成冰的过程中，冰块整体保持空间平移不变性，但分子却移向低能态形成了以d为距离单位的离散不变性。
 
时间晶体则是一种新的非平衡态物态，它是事件在时空中的有序排列，状态会随着时间自发周期重复。连续状态重复意味着打破了连续时间平移不变性，但由诺特定理可知能量将不再守恒，而这是不可能的。但它依然可以通过类似 Goldstone 模式，减少连续对称性实现离散（准）时间晶体：就像空间晶体遵循动量守恒，内部自发对称性破缺成了以 d 为距离单位的离散空间不变性一样，时间晶体通过约瑟夫森效应（Josephson effect）[34]，在保证能量守恒下，由完整时间平移对称变成周期为 2eV/h 的整数倍的对称，使内部有限状态不断自发周期性重复。——这种丧失连续时间不变性，变成离散对称性的宏观物态相即所谓的交换相。
 
图10：活性准时间晶体的相变，通过丧失时间平移对称性恢复离散对称性。
 
与手征相一样，交换相和混合相超越了特定尺度和领域模型，在非互易性同步和斑图形成中也能观察到它们。例如图11d、e中显示了涡流（反涡流）中的序参量 vA 和 vB 在固定方向角度拓扑缺变（topological defects）的快照。由于 vA 和 vB 不同的自推进速度，会导致涡旋对不断解开和湮灭的密度不同，从而形成调制态和调制行进（traveling modulated）态斑图：
 
图11：涡流和反涡流在不同序参量下拓扑缺变
 
以上流体力学过程上均可以用方程（8）来模拟：


其中奇异矩阵 LEP 代表了奇异点，M(vss⋅∇) 和 D∇2 分别模拟了流体的对流项（Convective term）和扩散项（Diffusive term）。
 

下面总结下基于PT对称性破缺三种不同运动模式下三种相变的关系：
 

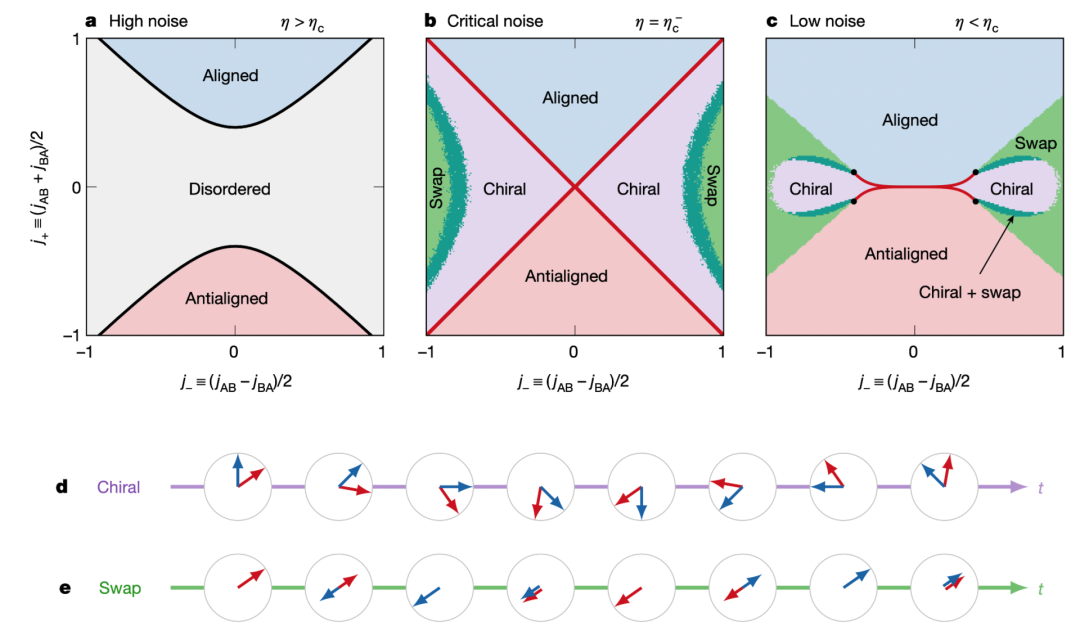
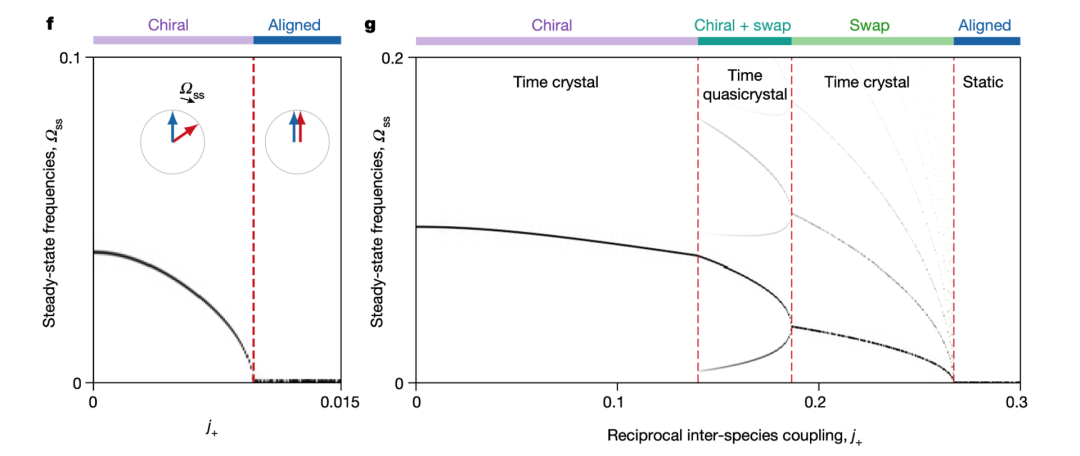
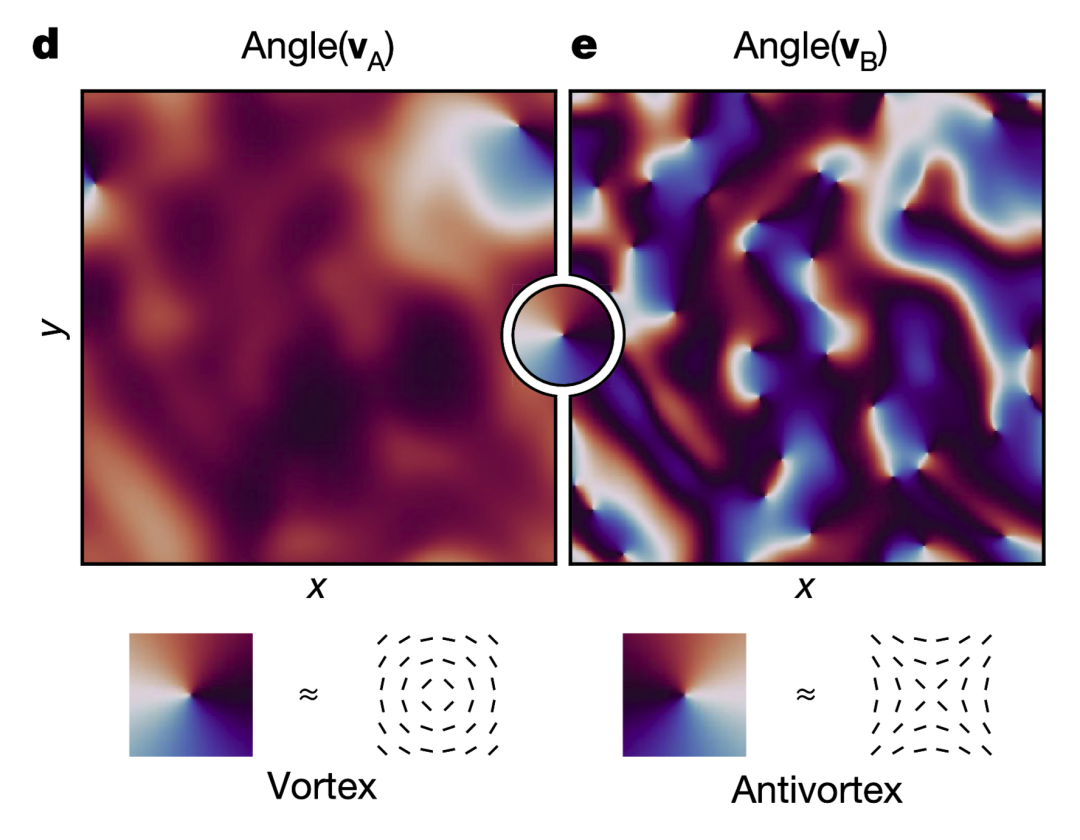
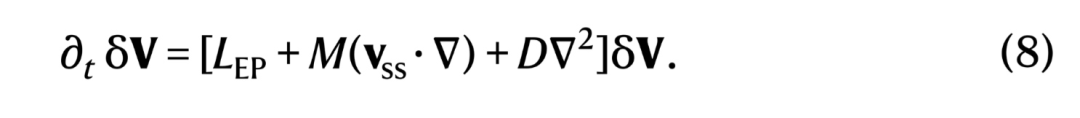
  • 手征、交换、混合三种不同相对比见视频：



  • 三种不同运动模式在三种相变的特征和例子，见对比表格：


*注释：行波态（traveling wave state）/ 行进态（traveling）/ 周期同步（periodic synchronization）/调制态（modulated）/ 调制行进（traveling modulated）/ 行波同步（PS+TW）

 
 



五、识别并分析非互易系统奇异点




那么如何识别一个具有连续对称性的宏观非互易系统呢？图12通过图示展示了这个过程。关键成分是：（i）非互易性，表现为不对称的宏观耦合，和（ii）自发的连续对称性破缺（自发对称性破缺）。

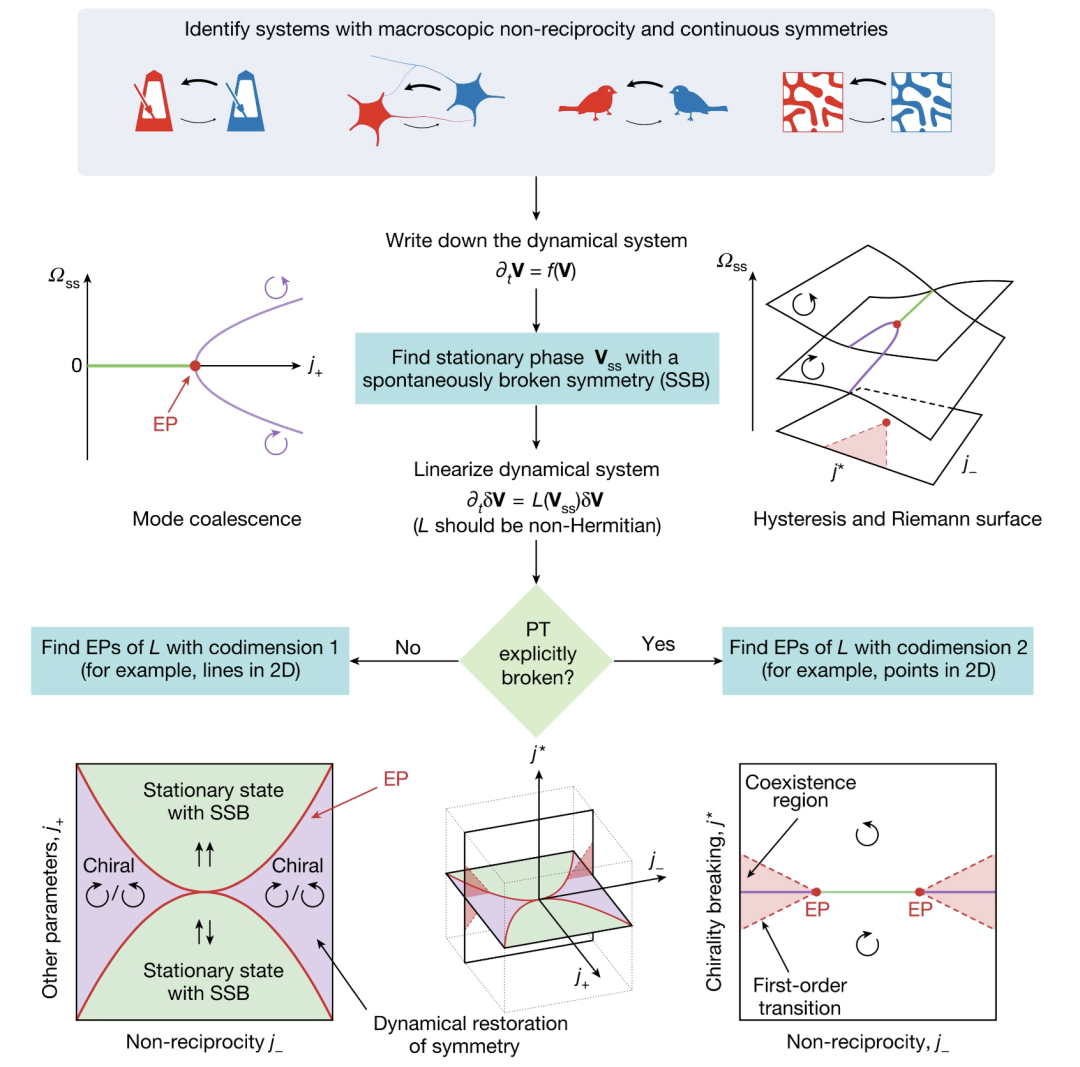
图12：识别和分析奇异点的可视过程

 
（1）首先确定一个系统是否是非互易作用的连续对称性系统。写下动力系统的序参量 V。然后找到一个能够自发对称性破缺（绿色区域）、与时间无关的稳态 Vss（基态），并对其线性化。若其雅各布矩阵线性算子L(V) 在 Goldstone 模式有一个零特征值，此时的奇异点（红点及连续红线）即标志着相变。
 
（2）在耦合参数 j 中区分出显性打破PT的 j*，并计算刻画非互易性的 j- 和 j+：
  • 当 j* = 0 时（图12左），从L中找到编码维为1的奇异点（二维参数空间）。在相变处 Goldstone 模式与一个阻尼模式相撞，这导致了以损失时间平移不变性为代价的对称性的自发动态恢复。在紫色的手征阶段，对应被打破的对称性的等效的两个稳态空间，以一个随机选择的方向（顺时或逆时针）行进。
  • 当 j* ≠ 0 时（下右图），奇异点编码维为2（三维参数空间），以上机制会与由 j* 设定序参量的明确旋转竞争，导致从二维奇异点开始扩展的浅红色区域，且其中顺逆时针状态共存，并以一阶相变和滞后为标志：其复频域形成一个了黎曼曲面（图13）：
 

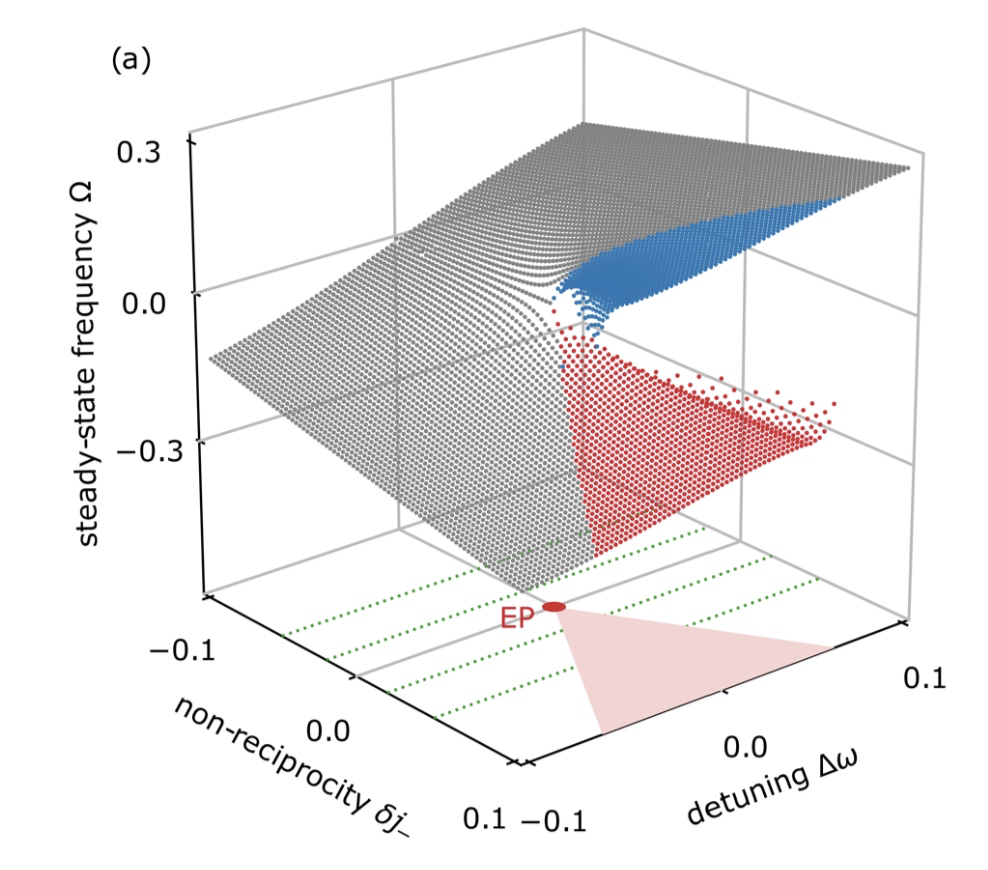
图13：手征 Kuramoto 模型的一阶相变和滞后形成的黎曼曲面[41]

 
 



六、总结：观测量、

守恒流、非互易性、对称性破缺与相变




这篇论文用包含时间参数的序参量场来讨论一般的非互易性作用的演化。正如诺特定理所示，在全局和连续系统中，守恒律和对称性有着一一对应关系，这也包括量子力学中某些离散对称性。而非互易性则来源于系统平衡态的远离和对称性破缺、或自发对称性破缺。
 
就本质而言，所有的对称性都源自某些基本的物理「不可观测量」（Non-observables）。例如，正因为弱相互作用下宇称不守恒，人类才打破了镜像对称性区分出了「左-右」；同样道理，由于空间均匀性和时间均匀性，绝对位置和绝对时间不可区分，所以就产生了动量守恒和能量守恒。
 
有些物理量我们可能永远无法观测，但有些可能限于我们人类的技术和观测水平。而一旦出现某些物理量可观测或不可观测，就意味着非互易和互易性作用之间发生了转化，就会导致某些对称性破缺或恢复（或为了满足数学形式人为弥补），从而可能形成新的物态和物相。
 
根据李政道的总结[35]，在物理学有四组主要的对称性或破缺的对称性：
 
1. 连续时空变换对称性：即洛伦兹协变性。如平移、转动和加速，对应动量守恒、角动量守恒、能量守恒等。这些都是全局对称性，针对是宇宙整体背景。

2. 离散变换：分立对称性。如空间反射 P（镜像、P宇称），时间反演 T，正反粒子共轭 C 宇称和 G 宇称，它们都是局域对称性，针对局域时空点的单独变换，给出物质相互作用。

3. 交换对称性：满足玻色一爱因斯坦统计，或满足费米一狄拉克统计，全同粒子的对称性（例如所有电子的全同性）。即交换任何两个电子，物理世界必定保持相同。由这个对称性可以自然得出泡利不相容原理。

4. 规范变换性。任何粒子集合的物理状态可以用一组复数波函数ψ来描述，包括大小和相位。规范场论认为，不同电荷两个状态之间的相位差永远不可能观测到，即波函数 ψ 乘以一个因子，物理世界保持不变：ψ → ψeiQθ。当因子分别是 1X1、2X2、3X3 的幺正矩阵时，对应以下三种对称性：
1）U(1) 对称性——电荷、超荷、重子数和轻子数的守恒律；
2）SU(2)（同位旋）对称性，质子和中子；
3）SU(3)（色和味）对称性，不同颜色的夸克，量子色动力学。
 
但这四组对称性中，只有前两组是严格的；第三组中的 CPT 的乘积是严格的，但每一个单独的离散对称运算和组合则是不严格的（如PT和CP）；在第四组中，只有 U(1) 对称性和色荷方面的 SU(3) 对称性，被认为是严格的。
 
这些对称和破缺的规律不仅仅针对基本粒子和作用量，在宏观和其它尺度也会产生新的对称性。比如对于铁磁，在温度升高相变前后的伊辛模型就具有不同的对称性。相变前，具有相同磁场方向的原子团的大小不同；但在相变后却是相同的——这形成了一种新的对称性共形不变性（conformal invariance）[36]：即平移、旋转和缩放原子网格，调整微观细节，系统的全局行为也不会改变。共形不变性是物理系统相变的普遍属性，因此相变前后（如降低温度），即可以看成是一种共形不变性恢复和破缺的过程。与之相应的共形几何研究的即保角变换下的不变量。
 
而近些年凝聚态物理在研究量子物体相变时，也发现一大类基于量子纠缠的量子物态。如超低温条件下二维电子气的分数量子霍尔态（fractional quantum Hall state）和量子自旋液体（Quantum spin liquid）。但特殊的是，不同的分数量子霍尔态具有相同的对称性，不能用传统的对称性破缺理论来描述。因此凝聚态物理学家转为用拓扑序（topological order）或量子序（无能隙）对这些物态进行分类。
 
不过，若以全息和纠缠的对称观点来看，这些拓扑序依然可以看成一种高阶代数对称性或范畴对称性（categorical symmetry）[37] [42]。因此杨振宁先生在回顾20世纪物理学发展时所言：“20世纪理论物理的三个主旋律：量子化，对称性，相位因子”，以及对称性支配相互作用的观点，在此意义上继续在当今物理学发展中有效[38]。
 
在下表中归纳了常见的可观测量、对称性、守恒律和不变性之间的关系，以供读者参考。



最后总结。对基础理论物理而言，不可观测量、一定数学变换下的不变性和守恒律、互易性关系、贯穿在每个对称性原理中，相对的则是非互易性作用、对称性破缺或形成某种新的对称性（恢复）导致的相变。
 
正如本文通过序参量场方法给出了基于PT对称性破缺及自发对称性破缺在非互易作用下宏观系统的推广，打通了从量子凝聚态到生物、社会集群、神经网络等微观粒子和宏观多体之间的桥梁一样，其余所有基本物理作用关系都可能以某种方式推广到更普遍的宏观系统中去。无论是基于传统对称性自发破缺思想，还是基于量子纠缠的量子物体的拓扑相变，都可以自觉运用类似思想，从而捕捉到和描述更多新的宏观物态和相变。

 

 

参考文献

[1] Shankar, S., Souslov, A., Bowick, M. J., Marchetti, M. C. & Vitelli, V. Topological active matter. Preprint at https://arxiv.org/abs/2010.00364 (2020).

[2] Uchida, N. & Golestanian, R. Synchronization and collective dynamics in a carpet of microfluidic rotors. Phys. Rev. Lett. 104, 178103 (2010).

[3] Saha, S., Ramaswamy, S. & Golestanian, R. Pairing, waltzing and scattering of chemotactic active colloids. New J. Phys. 21, 063006 (2019).

[4] Nagy, M., Ákos, Z., Biro, D. & Vicsek, T. Hierarchical group dynamics in pigeon flocks.

Nature 464, 890–893 (2010).

[5] Yllanes, D., Leoni, M. & Marchetti, M. C. How many dissenters does it take to disorder a flock? New J. Phys. 19, 103026 (2017).

[6] Lavergne, F. A., Wendehenne, H., Bäuerle, T. & Bechinger, C. Group formation and cohesion of active particles with visual perception–dependent motility. Science 364,  70–74 (2019).

[7] van Zuiden, B. C., Paulose, J., Irvine, W. T. M., Bartolo, D. & Vitelli, V. Spatiotemporal order and emergent edge currents in active spinner materials. Proc. Natl Acad. Sci. USA 113, 12919 (2016).

[8] Ivlev, A. V. et al. Statistical mechanics where Newton’s third law is broken. Phys. Rev. X 5, 011035 (2015).

[9] Lahiri, R. & Ramaswamy, S. Are steadily moving crystals unstable? Phys. Rev. Lett. 79, 1150–1153 (1997).

[10] Montbrió, E. & Pazó, D. Kuramoto model for excitation-inhibition-based oscillations. Phys.

Rev. Lett. 120, 244101 (2018).

[11] Sompolinsky, H. & Kanter, I. Temporal association in asymmetric neural networks. Phys.

Rev. Lett. 57, 2861–2864 (1986).

[12] Hong, H. & Strogatz, S. H. Kuramoto model of coupled oscillators with positive and negative coupling parameters: an example of conformist and contrarian oscillators. Phys.

Rev. Lett. 106, 054102 (2011).

[13] Malomed, B. & Tribelsky, M. Bifurcations in distributed kinetic systems with aperiodic instability. Physica D 14, 67–87 (1984).

[14] Coullet, P., Goldstein, R. E. & Gunaratne, G. H. Parity-breaking transitions of modulated patterns in hydrodynamic systems. Phys. Rev. Lett. 63, 1954–1957 (1989).

[15] Pan, L. & de Bruyn, J. R. Spatially uniform traveling cellular patterns at a driven interface.

Phys. Rev. E 49, 483–493 (1994).

[16] Fleury, R., Sounas, D. L., Sieck, C. F., Haberman, M. R. & Alù, A. Sound isolation and giant linear nonreciprocity in a compact acoustic circulator. Science 343, 516–519 (2014).

[17] Brandenbourger, M., Locsin, X., Lerner, E. & Coulais, C. Non-reciprocal robotic metamaterials. Nat. Commun. 10, 4608 (2019).

[18] Miri, M.-A. & Alù, A. Exceptional points in optics and photonics. Science 363, eaar7709 (2019).

[19]  Scheibner, C. et al. Odd elasticity. Nat. Phys. 16, 475–480 (2020).

[20] Helbig, T. et al. Generalized bulk–boundary correspondence in non-Hermitian topolectrical circuits. Nat. Phys. 16, 747–750 (2020).

[21] Kato, T. Perturbation Theory for Linear Operators 2nd edn (Springer, 1984).

[22] https://www.cantorsparadise.com/noethers-theorem-how-symmetry-shapes-physics-53c416c1f19c

[23] https://blogs.scientificamerican.com/observations/emmy-noethers-mathematics-as-hotel-decor/

[24 ] Parity–Time Symmetry Synthetic Lasers: Physics and Devices

[25] https://www.researchgate.net/publication/329807675_Dissipative_spinodal_decomposition_in_systems_with_nonreciprocal_effective_interactions

[26] 跨学科研究与非线性思维（第二版）(Interdisciplinary Research and Nonlinear)

[27] Order Parameters, Broken Symmetry, and Topology，https://arxiv.org/pdf/cond-mat/9204009.pdf

[28] Hohenberg, P. C. & Halperin, B. I. Theory of dynamic critical phenomena. Rev. Mod. Phys.49, 435–479 (1977).

[29] Oswald, P., Bechhoefer, J. & Libchaber, A. Instabilities of a moving nematic–isotropic interface. Phys. Rev. Lett. 58, 2318–2321 (1987).

[30] Faivre, G., de Cheveigne, S., Guthmann, C. & Kurowski, P. Solitary tilt waves in thin lamellar eutectics. Europhys. Lett. 9, 779–784 (1989).

[31] Brunet, P., Flesselles, J.-M. & Limat, L. Parity breaking in a one-dimensional pattern: a quantitative study with controlled wavelength. Europhys. Lett. 56, 221–227 (2001).

[32] Winfree, A. T. The Geometry of Biological Time (Springer, 2001).

[33] Khemani, V., Moessner, R. & Sondhi, S. L. A brief history of time crystals. https://arxiv.org/abs/1910.10745 (2019).

[34] https://en.wikipedia.org/wiki/Josephson_effect

[35] 李政道《对称与不对称》

[35] 《数学家证明相变的对称性：从旋转对称性到标度不变性》https://mp.weixin.qq.com/s/Pt-mJJ8t8QHm2kz1xuWUgA

[37] Algebraic higher symmetry and categorical symmetry – a holographic and entanglement view of symmetry https://arxiv.org/abs/2005.14178

[38] 《杨振宁：二十世纪理论物理学的主题旋律》https://mp.weixin.qq.com/s/pB-xeH7qlcy-rcbNfhueQQ

[39] http://www.scholarpedia.org/article/Gauge_invariance

[40] What is Nonreciprocity? 10.1103/PhysRevApplied.10.047001

[41] Non-reciprocal phase transitions，Supplementary Information section XI.

[42] Thidjin Tzoh，拓扑序与量子序


（参考文献可上下滑动查看）



复杂科学最新论文


集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅：



推荐阅读



点击“阅读原文”，追踪复杂科学顶刊论文