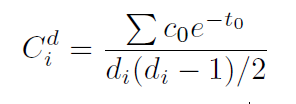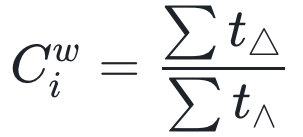复杂系统的动态效应决定了研究的复杂性,我们既不能只观察某一时刻的状态,也不能对复杂系统完全平均化处理。时间作为复杂系统演化过程中的重要维度,起到了何种作用?本文整理自同济大学李翔教授在集智俱乐部网络科学课程第三期的讲座,介绍了时效网络研究范畴和几项具体的时效网络研究,讨论了时效网络的研究意义,为网络科学研究提供了新视角。
研究领域:复杂网络,时效网络
李翔 | 讲者
段月然 | 整理
邓一雪 | 编辑
有一段传统相声叫《关公战秦琼》。不过熟悉历史的朋友都知道,关羽是三国时期的名将,秦琼是隋末唐初的大将,两个人相隔几百年,如何让关公战秦琼呢?
这个典故实际上是用来讽刺不切合实际而盲目指挥的人,关公和秦琼出生于不同年代,根本不可能相战,但由于关羽和秦琼身上相似的特质会不禁引起人们对英雄的比较。在网络科学中,传统的复杂网络建模方式若仅考虑两个主体的相似性而强加关联,而忽略事件(交互)发生的顺序,难免会发生关公战秦琼这种不符合实际的状态。如何处理这种跨越时间、跨越空间的相遇呢?也许时效网络能给出答案。
最初 temporal network 的名称概念进入国内的时候,国内学术界并无统一的中文译名。复旦大学CAN研究室早在2011年就定下来使用“时效”网络来对应于英文的Temporal network,而国内学者也不乏将它翻译为时序网络或时变网络等。那么“时序”和“时效”的区别是什么呢?我们来看几个概念:
时序(time-order):强调了时间的发生顺序,在一个带有时间戳的复杂网络中,时间顺序就天然存在了。
时变(time-varying):通常假定等周期采样,两次获取数据的间隔是等周期的。而在 temporal network 的研究中,数据并不一定是等周期的。
时间演化(time-evolving):演化这个词的出现似乎更早,在 Barabási 提出BA生成模型时就已经有了演化的概念,而演化模型并不一定都是 temporal network。
无论是时序、时变还是时间演化,它们都反映了 temporal network所表征的某一方面时间特征属性。然而,伴随着人类动力学研究的时效网络,在引入时间维度来刻画连边属性的时间特征时,还覆盖了间隔时间、持续时间等新的时间维度性质(例如,阵发(burst)特性)。此外,在后续人们的研究中还提出来time-ordered graph(中文名:时序图)的方法,用于专门刻画时间先后顺序的关连表达,有兴趣的同学可以检索相关的论文。时至今日,再把temporal network直译为时序网络,显然都有以偏概全之嫌了。
我们来看 Petter Holme 在 temporal network 的论文中所提到的例子:假设信息从A开始传递,时刻6第一次传递到B,B有两条路径分别到C和F,由于B只在1和3时刻向F传递信息,因此A的信息无法传递给F。不过,B依然可以在时刻8向C传递信息,以此类推。如果这是一个静态网络,A和F有3条路径可以连通,但在这样一个 temporal network 中,由于信息传递顺序所存在的时间效用,A的信息无论如何都无法传递给F。
因此,用“时效网络”的中文译名来描述 temporal network 显然更贴切,也更符合信达雅的翻译要领。

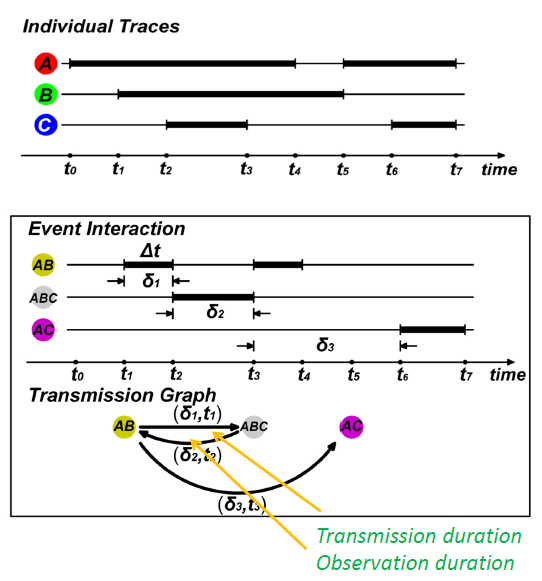
图1. 时效网络的两种可视化方式
P. Holme , J. Saramaki (2012), Temporal networks, Physics Reports, vol. 519, p. 97
时效网络相较于静态网络可以更好地描述人类交互行为的动力学,这可以通过以下两个例子体现。
一项研究通过统计复旦大学中所有行政楼、体育馆、教学大楼等几个主要建筑物用户访问 WiFi 的数据,统计学生和教师的接触情况(这有利于研究一些传染病的传播过程,这个数据集名为“FudanWiFi09”)。图2展示了时效接触网络的构建过程和与传统聚合型接触网络的区别。
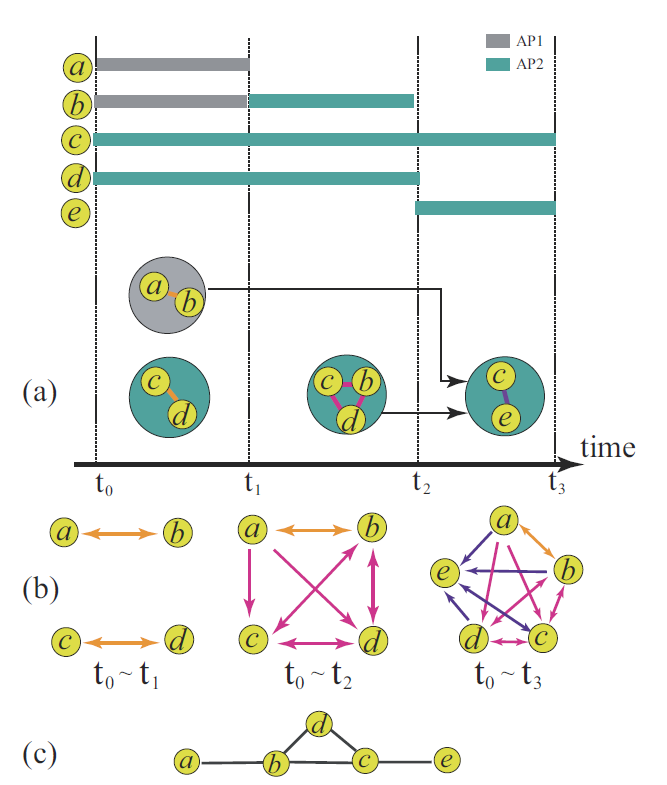
图2. 构建时效接触网络和聚合接触网络。(a) 通过WiFi访问日志转换成对应的交互事件。AP表示WiFi接入点,黑色箭头展示了不同交互事件中个体的时效接触。(b) 构建出相应的时效接触网络,根据边的更新时间着色。(c) 构建出相应的聚合接触网络。
网络可达性定义为节点i在给定观测时间下实际可接触到的节点的数量。类似图1的情况,传统的聚合网络在接触可达性上会出现巨大的偏差。下图也说明了这一点:通过时效接触网络经过30天,平均可达性约为80%,而通过聚合接触网络只需要两三天就可以达到100%的可达性。而时效接触网络下的最大可达性也需要7天左右才能感染整个网络。因此,如果在类似传染病等具有时效接触型网络的研究中使用传统聚合模型就会产生巨大的偏差。
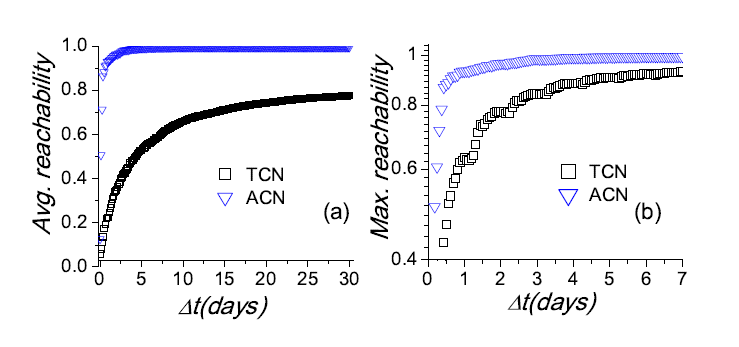
图3. 时效接触网络和聚合接触网络的平均可达性和最大可达性比较
Y Zhang, L Wang, YQ Zhang, X Li, Towards a temporal network analysis of interactive
WiFi users, EPL , 2012, 98, 68002.
网络中个体间这种具有电子标签的二元交互是一种理想的情况,更多的情况是由一个事件产生了组交互的状态,个体因为事件开始发生接触,又因为事件结束离开。这种因为事件交互而产生的组交互也可以用时效网络来刻画。
图4展示了一种新的时效网络建模过程,这次个体不再是在某个时刻出现,而是某一时间段持续出现,将具有重叠时间的个体交互看作一个事件交互(Event Interaction, EI)。构建的传播图是以事件交互为节点,边具有三种规则:(1)source 都在 sink 之前;(2)事件交互中个体一致;(3)当一个 sink 之前有多个 source,任何一组在 source 和 sink 之间的同一事件的用户都不会产生交互。这三种规则基本遵循了1978年 Leslie Lamport 提出事件“发生”先后关系的三条准则。
1978年,Leslie Lamport 给出了定义事件中“发生”的先后关系:
1. 如果a和b是同一过程中的事件,a出现在b之前,那么a发生在b之前。
2. 如果a和b是两个不同过程中的事件,a是b的原因,那么a发生在b之前。
3. 如果a发生在b之前,b发生在c之前,那么a发生在c之前。
Leslie Lamport (1978), Time, Clocks, and the Ordering of Events in a Distributed System, Communications of the ACM, vol. 21, pp. 558-565.
通过传播图的定义可以发现,一部分静态图中不重要的“叶子”节点在传播图中会成为十分重要的hub节点。这种组交互涉及到了网络的高阶状态,这里通过定义组交互为一个节点来处理网络中高阶交互的状态,还可以选择高阶网络建模,会有更多有趣的发现。
1. 时效网络中的节点重要性排名问题
之前的介绍表明,静态图中一些不被关注的叶子节点在时效网络建模下会变得很重要,如果忽视这些节点可能会带来一些麻烦。在网络中衡量节点重要性最简单的方式就是计算节点的度,时效网络中节点的度的定义也会有所不同。回到图4构建的传播图,每个用户的时效度可以定义为用户所在的所有事件交互中的最大值。
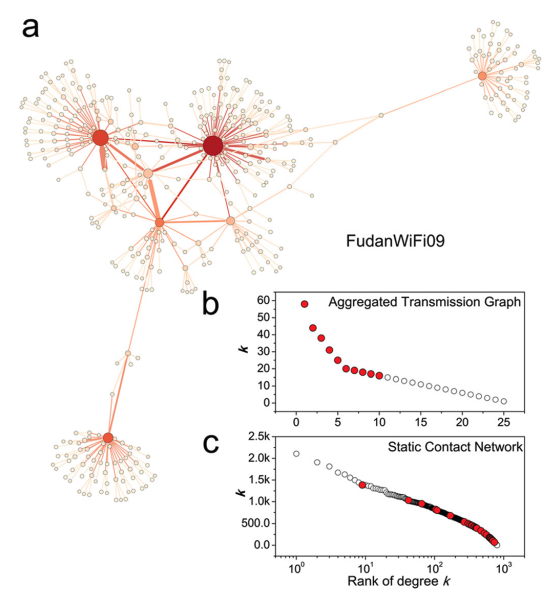
图5. (a)“FudanWiFi09”数据集中传输网络的形态(红色为hub节点);(b) 传输网络中节点的时效度分布(该节点是hub节点的组成部分被标记为红色);(c)静态接触网络中节点的度分布(该节点是传输网络中hub节点的组成部分被标记为红色)
图5展示了在“FudanWiFi09”数据集下具有时间信息的传输网络和静态接触网络度分布情况。我们可以观察到,在传输网络中具有重要作用的用户(图5(b)红色节点)在静态接触网络中几乎都是低度节点(图5(c)红色节点)。这说明,静态接触网络中通常被忽略的低度节点可能参与了时间结构下具有重要作用的hub结构。
我们可以通过一些简单的参数来描述一个网络,如节点数、边数、路径长度等。在对网络结构的研究中,网络的集聚系数用于衡量网络的节点聚集的程度,也就是网络的稠密程度。网络集聚系数从宏观的角度观测了网络中闭合三角形占比情况,但想要了解网络中三角形的具体形态,则需要引入模体的概念。对模体这种中观结构的分析有助于了解不同网络的特征和功能。下面将具体介绍时效网络的集聚性测量和时效网络中模体的识别。
这里介绍两种时效网络集聚系数的计算方法,分别为时间滞后集聚系数(Temporal-delayed Clustering Coefficients)和时间加权集聚系数(Temporal-weighted Clustering Coefficients)。
J Cui, Y Q Zhang, X Li, On the clustering coefficients of temporal networks and epidemic dynamics, IEEE Int. Symposium on Circuits and Systems (ISCAS 2013), 2299-2302.
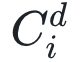 用于表示节点i的集聚系数(这里只以节点集聚系数的计算方法举例),c0表示时效三角形的形成状态,
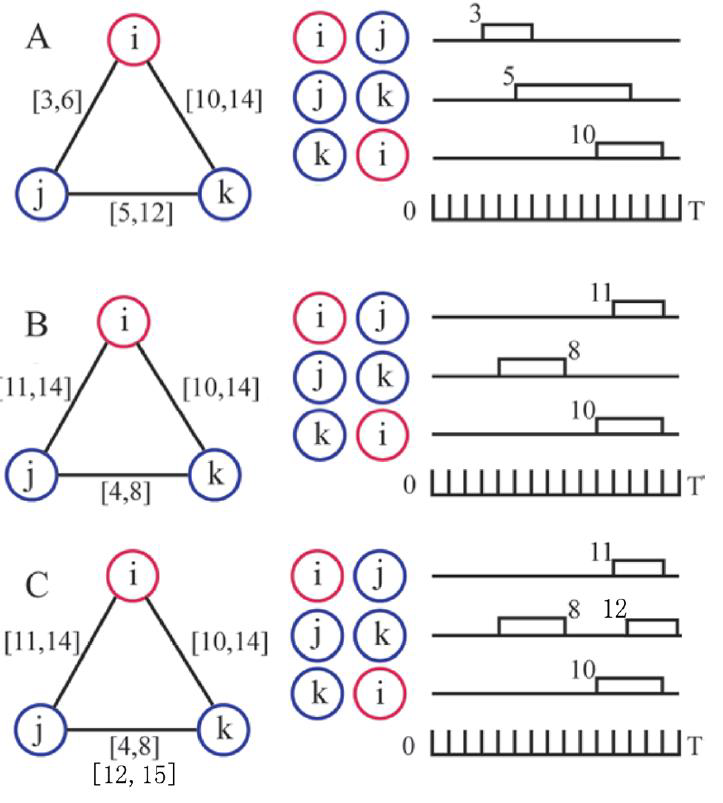
用于表示节点i的集聚系数(这里只以节点集聚系数的计算方法举例),c0表示时效三角形的形成状态,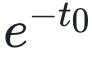 表示时间滞后性。图6展示了时效三角形形成模式:图6A展示的三角形信息通过 i-j-k-i 形成了通路,所以c0=1;图6B展示的三角形中,j-k 结束于 i-j 和 k-i 出现之前,无法形成信息通络,则c0=0;而在图6C中,j-k 在 i-j 和 k-i 出现后又重新出现,也能够形成信息通络,则c0=1。t0表示从观察的起始时间到形成一个时效三角形的时间间隔,
表示时间滞后性。图6展示了时效三角形形成模式:图6A展示的三角形信息通过 i-j-k-i 形成了通路,所以c0=1;图6B展示的三角形中,j-k 结束于 i-j 和 k-i 出现之前,无法形成信息通络,则c0=0;而在图6C中,j-k 在 i-j 和 k-i 出现后又重新出现,也能够形成信息通络,则c0=1。t0表示从观察的起始时间到形成一个时效三角形的时间间隔,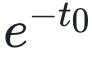 描述了需要多长时间形成一个时效三角形。
时间加权集聚系数更类似于传统集聚系数的计算方式,其数学定义如下:
描述了需要多长时间形成一个时效三角形。
时间加权集聚系数更类似于传统集聚系数的计算方式,其数学定义如下:
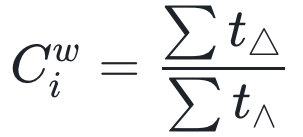
其中t△表示三条时效边重合持续时间,而t∧表示以节点i为中心的三元组存在的持续时间,其数学定义展示在图7中。
对比静态网络的集聚效应,在“FudanWiFi09”数据集使用静态网络的集聚系数计算方法展示出较大的集聚性。而加入时间信息后,时效接触网络的集聚性明显降低,尤其是在时间滞后集聚系数的测度下。对实证数据的仿真也证明,时效网络集聚性测度可以降低传播阈值,传染规模也受到时效网络可达性的限制,可以为预测人类活动中疾病流行和预测提供新视角。
网络模体(Motif)是网络的子图,在实际网络中模体出现的可能性比随机网络的期望值要高。模体是网络的基本拓扑之一,它的大小介于网络个体和社团之间,一般由少数几个节点连接构成。模体揭示了网络的演化规律,它是社团内部成员之间基本的连接模式。
模体目前已经广泛应用于贸易网络、互联网、社会网络、交通运输网络、生物系统等。网络模体的定义是比较清晰简单的,目前模体研究的难点尤其是时效模体主要为如何快速有效地识别网络模体。
Lauri Kovanen等人(2011)定义了时效网络模体,他们认为时效模体是一种具有相同结构的子图,这种相似性也包括事件的时间顺序的相似性。挖掘网络中带有时间信息的模体可以更有效地理解模体在网络中的功能,也可以帮助我们检测或预测大规模社会群体中的突发行为特征。
L. Kovanen, M. Karsai, K. Kaski, J. Kertesz and J. Saramaki (2011) Temporal motifs in time-dependent networks, J Stat Mech 2011: P11005.
本次课程详细地介绍了时效网络的基本概念、建模方法和相关应用。由于复杂系统的动态特征,对系统进行时效网络的建模会引出更多新的研究问题,也将在时间维度下得到与静态模式下完全不同的结果。
无论是网络的时变特征、演化模式,还是网络的时效性,加入时间信息的网络更贴近真实系统,其研究也更灵活而复杂,我们列出一些时效网络的未来供读者探讨:
时效网络用于研究流行病研究一般可分为两类:我们可以将带时间标签的数据用于建模接触网络来模拟传染病传播情况;也可以在时效网络上建模出一个具有时效性的传播模型用于模拟传染病传播情况。
前文介绍了时效网络和静态网络在网络可达性上具有较大的差异,而网络的能控性首先依赖于网络的可达性。无论对实证数据可控性的研究还是对一个带有时间信息的控制方程的研究,时效网络都是值得关注的重要方法。
-
Temporal network + 社区时间不变性
时间变化的背后是否具有一些不变的信息也值得我们思考,比如网络社团。如何界定随着时间变化但依然保持稳定的网络结构还有待研究。
除此之外,时效网络与网络重构、人类动力学、预测等问题的结合也都值得我们关注和研究。这里给出了一些利用时效网络解决问题的案例,如何更好地利用时间信息和时效性解决更多实际问题还有很多开放和值得探索的方向。
-
Cong Li, Yuan Zhang, Xiang Li , Epidemic threshold in temporal multiplex networks with individual layer preference, IEEE Trans. Network Science and Engineering , 2021, 8(1), 814-824.
-
Cong Li, Jing Li, Xiang Li , Evolving nature of human contact networks with its impact on epidemic processes, Complexity , 2021, vol. 2021, article ID: 6643658
-
Wenjing Wang, Xiang Li , Temporal stable community in time varying networks, IEEE Trans. Network Science and Engineering , 2020, 7(3), 1508-1520.
-
Yiqing Zhang, Xiang Li, Athanasios V. Vasilakos , Spectral analysis of epidemic thresholds of temporal networks, IEEE Trans. Cybernetics , 2020, 50(5), 1965-1977.
-
Cong Li, Shumin Zhang, Xiang Li, Can multiple social ties help improve human location prediction? Physica A , 2019, 525, 1276-1288.
-
Xun Li, Xiang Li, Reconstruction of stochastic temporal networks through diffusive arrival times, Nature Communications , 2017, 8, 15729.
-
Peng Yao, Baoyu Hou, Yujian Pan, Xiang Li, Structural controllability of temporal networks with a single switching controller, PLoS ONE , 2017, 0170584.
-
Baoyu Hou, Xiang Li, Guanrong Chen, Structural controllability of temporally switching networks, IEEE Trans. Circuits and Systems I , 2016, 63(10), 1771-1781.
-
Yiqing Zhang, Jing Cui, Shumin Zhang, Qi Zhang, Xiang Li, Modelling temporal networks of human face to face contacts with public activity and individual reachability, European Physical Journal B , 2016, 89:26.
-
Yujian Pan, Xiang Li, Structural controllability and controlling centrality of temporal networks, PLoS ONE , 2014, 9(4), e94998.
个人简介:同济大学教授,上海自主智能无人系统科学中心复杂网络与智能系统研究所主任,复旦大学自适应网络与控制(CAN)研究室主任。1997年毕业于南开大学计算机与系统科学系获学士学位,2002年毕业于南开大学自动化系获博士学位。国家杰出青年科学基金获得者,国家万人计划科技创新领军人才,上海领军人才。主要研究领域为复杂网络科学与集群智能。曾获2005年IEEE电路与系统学会Guillemin-Cauer最佳论文奖、2008年上海市自然科学一等奖、2015年国家自然科学二等奖、上海市第五届十大青年科技英才、中国自动化学会首届青年科学家奖、2019年中国自动化学会TCCT陈翰馥奖等。
CAN研究室主页:http://can.fudan.edu.cn
网络科学集智课堂第三期报名中
从数学建模到多学科应用
从现实社会的关系网到虚拟的互联网,从线下到线上,我们的生活始终没有脱离复杂网络。真实的复杂网络从其诞生开始就不断地演化着。网络节点不断地增加,节点之间的连接不断地增长。然而,复杂网络的形成机制是什么?具有什么样的演化规律?它们的演化机制对网络的功能和动力学行为有什么影响?为了回答这些问题,科学家们对复杂网络的探索从未停止。
网络科学是一个蓬勃发展的崭新交叉学科,可以看做复杂系统的骨架,核心是研究各种大型复杂网络之间的共性和处理它们的普适方法,其研究对于发展复杂系统的基本理论及构建产生了极大的推动作用。
网络科学的第三个十年,已经过去了几年。从国内外网络科学研究的发展趋势来看,各种各样的更复杂的网络模型和结构以及高阶相互作用动力学引起了人们的极大兴趣。为了回应这种迫切需求, 我们网络科学第三期课程将围绕复杂网络的数学建模与应用进行多角度的介绍。
集智学园特邀陈关荣、樊瑛、周进、李翔、张江、闫小勇、刘宗华、石川、虞文武、赵海兴、史定华加入打造第三期课程,欢迎你的加入。
点击“阅读原文”,报名课程