论文题目：

Indirect influence in social networks as an induced percolation phenomenon

论文链接：

https://www.pnas.org/doi/10.1073/pnas.2100151119

一、研究背景：社交网络中的间接作用

渗流理论是统计物理学中的重要理论之一，它通过研究网络节点之间的不同交互作用，很好地捕捉系统中的各种动力学现象，尤其是相变等系统行为。目前已有的相关研究大多都聚焦在节点间的直接作用机制建模上。而最新研究表明，在许多复杂系统中，间接相互作用不仅在其传播动力学中发挥着关键作用，也对网络结构的演化和涌现有着重要影响。例如，对于吸毒、酗酒、肥胖等许多社会行为的传播，一个人可以受到“三度”（即朋友的朋友的朋友）以内的影响。

尽管间接影响在各类真实系统中无处不在，但很少有学者研究间接影响发生的确切机制，或直接影响与间接影响之间的相对强度。在理论方面，目前尚无相关研究基于渗流理论模型来描述间接影响的潜在机制。

近日，南方科技大学胡延庆团队在PNAS发表的最新科研成果弥补了上述研究空白。研究者通过对科学家合作网络的历史数据分析，发现间接合作者对研究领域的影响更大，并基于渗流理论建模揭示网络中间接作用的影响力机制。

二、科学家合作网络：

间接影响对科学家选择方向影响更大

为了研究经验网络中相邻影响的确切机制及其直接或间接性质，该文章利用论文数据集建立科学家合作网络，分析科学家的研究领域如何受到他们的直接（最近）邻居和间接（次最近）邻居的影响。在合作网络里，“行为”指科学家的研究领域，“行为的传播”指科学家留在既定领域或转向新兴领域的倾向。

       表1. 科学家合作网络数据的基本信息。研究选择了物理学中的四组领域：混沌与复杂网络、相变与复杂网络、低维结构的电学性质（EPLD）与低维结构的光学性质（OPLD），以及碳纳米管与石墨烯。每一组的后者（新领域）都吸引着来自前者（旧领域）的科学家。

合作网络中的每一位科学家都被视作网络中的节点。将尚未在新领域发表文章的科学家定义为“影响者”，状态记为1，其他科学家被视为“受影响者”，分别计算每个节点的的直接和间接“影响者”数量。节点i的直接影响者数量为状态是1的邻居数。间接影响则是考虑邻居“影响者”的邻居“影响者”数量最大值m_i（又称诱导指数），以及邻居“影响者”拥有的最大度值d_i（又称度指数）和直接影响指数（又称K核指数）。图1为上述各指数的可视化说明。

图1.“受影响者”i的诱导指数（间接影响指数）m_i  、K核指数（直接影响指数）和度指数d_i计算示例。直接影响指数=2对应节点i的2个状态为1的一阶邻居节点数；诱导指数m_i=3对应节点j的3个状态为1的一阶邻居节点数（即反映节点i的二阶邻居状态）；度指数d_i=6对应节点j的度为6。

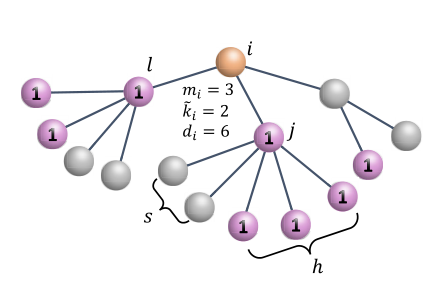
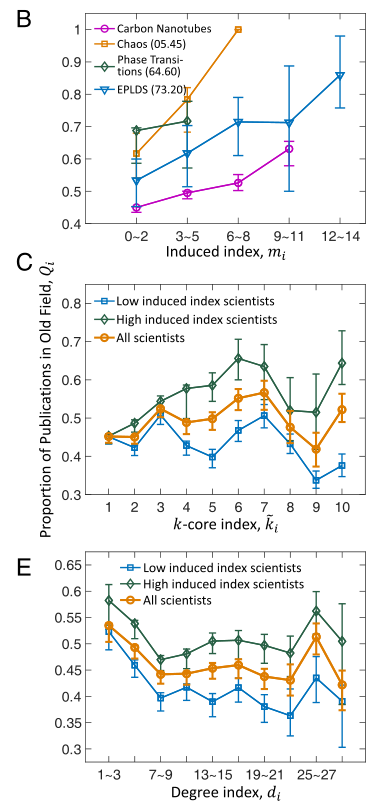
对每个“受影响者”计算在旧领域发文数和总发文数的比值Q_i。Q_i值越高，则说明受那些“扎根”于旧领域的“影响者”的直接影响与间接影响程度越大。图2反映了各指标与受影响程度的关系。Q_i随着诱导指数（间接影响指数）m_i增加，但与K核指数（直接影响指数）或度指数d_i关系较一般。这表明科学家选择研究方向时，间接影响起主导作用，而非直接影响。事实上，研究还发现节点i和h通过节点j（如图1）更有可能在旧领域中合作，这意味着，Q_i和诱导指数m_i的相关性确实能调解合作关系。

图2. 科学家合作网络中，受影响程度与诱导指数（间接影响指数）m_i、K核指数（直接影响指数）、度指数d_i的关系。

三、诱导渗流模型描述网络中的影响机制

研究者们从上述的科学家合作网络中观测到，相对于直接合作者，间接合作者对科学家研究领域的变化影响更大。在该发现的基础上，文中提出诱导渗流模型（induced percolation）来描述网络中的间接影响机制，刻画其与系统宏观行为之间的关系。例如，对于前文的科学家合作网实证现象，诱导渗流模型可被用来解释在何种间接合作情况下，一个科学家或某个科研群体将从原来的研究领域转到新兴领域，或是某个科学家群体将整体都转向新兴领域。

在诱导渗流模型中，每个节点的状态由整数值0或1表示。最初，网络中所有节点的状态均设置为1。最基础的诱导渗流模型的前提是，如果一个节点的诱导指数m_i大于特定阈值m，则节点状态会以h(m_i)=1的概率转为1，反之则转为0。数学表示为：

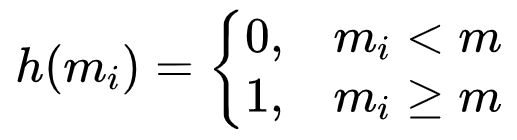
如图3展示了阈值m=2的情景下的诱导渗流机制，节点i保持状态为1的条件是：节点i的至少一条入边来自状态为1的节点（如节点j），并且节点j又有至少m条入边来自状态为1的节点。否则，节点i将在下一时刻状态变为0。m个节点对节点i的影响定义了它们之间的间接交互。在这种间接作用机制下，某些节点将在后续的时间步将其状态从1更改为0，直到无法再进行更改。与以往的键渗流、点渗流或K核渗流相比，诱导渗流的关键在于节点当前的状态不仅受最近邻的影响，还会受到若干次最近邻的影响。

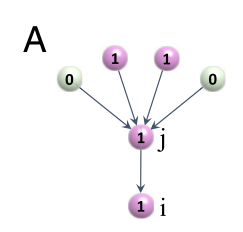
图3. 阈值m=2情景下诱导渗流机制示意图

为描述系统的相变行为，该研究以GOUT（giant out-component）的规模作为表征系统相变的宏观量。例如，在科学家合作网络实证研究中GOUT的规模能反映留在旧领域的科学家数量。GOUT中的任何节点都可以到达系统中最大强连通片，在以往的各类型传播动力学研究中，GOUT能对应于最大的传播覆盖率，并且在给定的传播机制下可作为网络连通性的指标。

诱导渗流过程的相变可以在随机网络上进行解析研究。如图4，定义递推变量x和y，x表示随机选择有向边时，边的起始节点处于激活状态（状态为1）的概率，而y表示随机边使其终点节点处于激活状态的概率。x和y的具体表达式都可以用联合分布P(k_in, k_out)来表示，  P(k_in, k_out)表示随机选择一个节点具有k_in入度和k_out出度。在此基础上，研究者们利用x和y推导出描述GOUT规模的序参量P_∞的表达式，并基于该序参量开展后续分析。

图4.渗流相变关键变量x和y示意图

四、诱导渗流模型的相变

在建立模型理论框架后，研究者在多个具有不同性质的网络中进行诱导渗流实验，并观察各网络中的相变情况。结果表明，对于相同的网络连接模式，相变的类型或顺序取决于边的方向性，即相变本质上是各向异性的。在有向网络上，当m>1（m=1是典型的键渗流情况）时，诱导渗流表现出不连续的（一阶）相变。在无向网络上，相同的渗流过程总是导致连续（二阶）相变。

这些结果与之前的网络渗流模型形成了鲜明对比，之前从未发现网络中边的方向性会从根本上改变相变的类型。这意味着之前广泛研究的渗流模型可能大大低估了边方向不对称性对系统宏观行为的影响。这一观察结果蕴含着更多意义，在生态和社会网络等复杂系统中，发生剧变的可能性可能比原有渗流模型预期的要大得多。

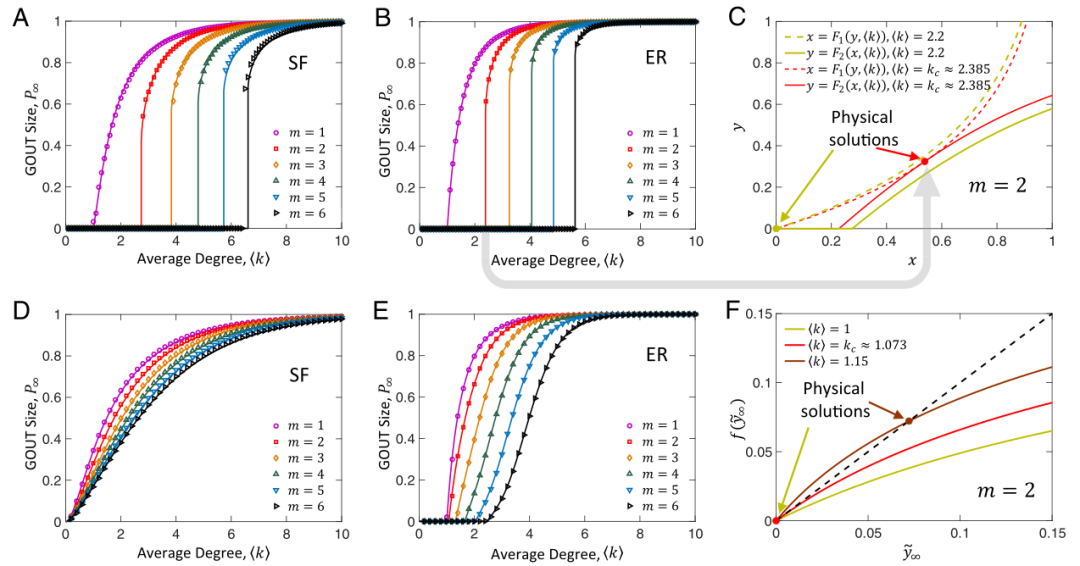
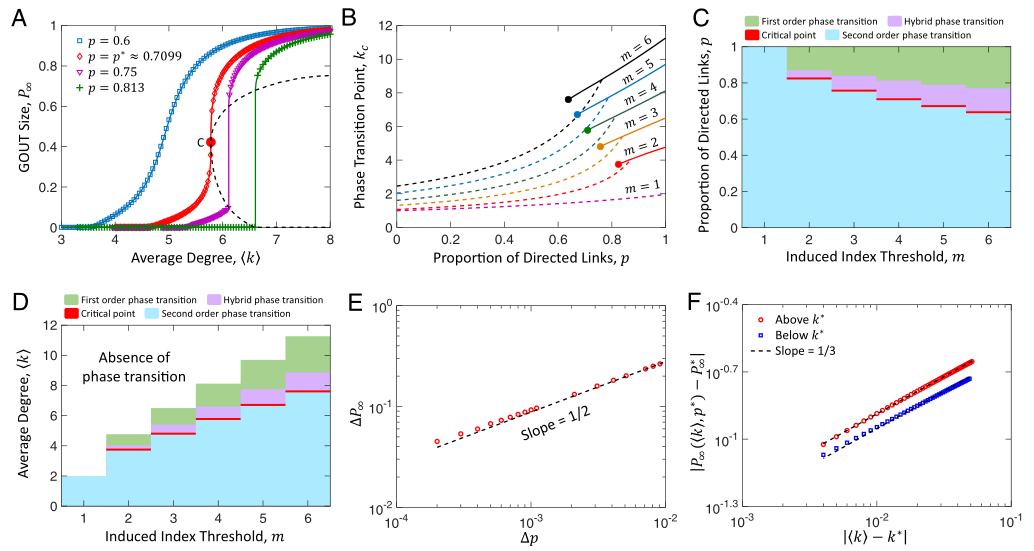
当网络为由有向边和无向边组成的混合网络时，边的方向性引发的各向异性会导致丰富而复杂的行为。具体地说，混合相变出现在具有一定数量的定向边的系统中，即在有向、无向、有向无向混合的网络中会分别出现一阶、连续、混合相变。图6子图A和B显示，通过增加网络中有向边的占比p，序参量P∞随着平均度的增加而增长，从连续相变到包含连续和非连续的混合相变。研究将混合相变首次出现的临界点标记为C点（如图6子图A所示），并发现了一组标度律，使得GOUT与朗道平均场理论预测的C点附近的其他量关联起来。

五、总结与讨论

在不同的社会和生态系统中，越来越多的经验证据表明，间接相互作用在塑造系统的动态行为中起着关键作用。该研究对科学家合作网络的实证研究进一步表明，在行为传播中，间接影响可以超过直接影响。然而，现有的几乎所有模型都关注个体之间的直接相互作用，而间接相互作用的一般影响尚未被研究。该研究首次提出诱导渗流来描述间接相互作用，并发现间接相互作用会产生大量新现象，导致各种可能的相变。这种间接机制导致了与直接作用截然不同的传播结果。

总的来说，该研究证明了网络中有向边的数量决定了相变的顺序，在有向、无向、有向无向混合的网络中分别出现一阶、连续、混合相变；在二级相变的临界点附近，网络的连通片规模会出现奇特的震荡行为。尽管该实证研究只揭示了两度以内的一种影响机制，但可以将其视作为“三度影响”提供特定传播机制的理论基础，并能有助于学者们更好地理解其相关的动力学过程和宏观传播结果。

集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅：

点击“阅读原文”，追踪复杂科学顶刊论文