论文题目：

Nonnegative Decomposition of Multivariate Information

论文链接：

https://arxiv.org/abs/1004.2515

一、如何量化复杂系统中的相互作用？

想象这样一个场景：我们收集到了很多人的身高、体重和性别的信息，现在让我们来训练一个神经网络模型来建模数据中的关系，以身高和体重作为输入，以性别作为输出。这是一个比较基础的机器学习场景。然而我们的问题是，能否在训练之前，就大概估计出每个变量的相对重要性？

理解这个问题的一个基本思维是，若特征之间存在非常复杂的相互作用，则我们需要很多的参数去拟合这种相互作用，否则，只需很少的参数对特征进行线性拟合即可。那么我们能否量化这种相互作用的复杂性呢？

让我们再来看一个场景：社会复杂系统的归因是一个困难的问题。一个典型的例子是，人们常常把萨拉热窝事件定义为一战的导火索，导火索是事情的直接起因，但我们知道真实的情况必然更复杂得多。那么我们能否有一种定量的方法去回答这样的问题：到底是某个事件单独促成了战争的爆发，还是多个事件共同促成了战争的爆发？

从某种视角来看，复杂系统可以看做存在相互作用的多变量系统。而信息论视角是理解变量之间相应关系的重要视角，因此人们发明并拓展了一系列方法，将信息论的思维应用到对复杂系统的理解上。例如，针对两个变量之间的相互作用，我们可以使用互信息（Mutual Information）来衡量当一个变量被观测后，另一个变量的不确定性（熵）的减少。但这种工具的适用场景相当有限，当变量数量增多，其相互作用机制变得复杂时，由于大量变量之间有可能存在协同效应（synergy），因此，我们除了计算原始变量之间的互信息，还要计算变量的两两组合，甚至更多组合之间的互信息。另一方面，在预测问题中，不同自变量之间有可能共享相似的信息，那么不同变量之间共享的这部分信息到底对预测起到了多大作用呢？

为了理解多变量相互作用情况下的信息结构，人们对互信息做了一系列拓展，发明了多种新的工具以分析复杂的相互作用，并试图将这些工具应用于对复杂系统的理解中。

本文将介绍多个源（source）变量作用于一个目标（target）变量时的一些信息分解工具，我们将从互信息出发，进一步讨论多变量情况下的互信息面临的困境，并引入信息的非负分解方法来更好地理解多对一情况下的信息结构。

二、互信息的局限性

信息论奠基人香农（Shannon）认为，“信息是用来消除随机不确定性的东西”。也就是说衡量信息量大小就看这个信息消除不确定性的程度。通过将信息与事件发生的概率结合在一起，香农率先对信息量进行了度量：即信息量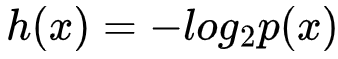，x 为随机变量 X 的一个可能取值，p(x) 表示 X 取值为 x 的概率，h(x) 代表 X 取值为 x 这一事件的信息量。进一步，香农提出了信息熵的概念来衡量一个随机变量可能产生的信息量的期望，即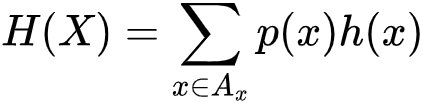。我们也可以将信息熵理解为对事物的不确定性的度量：信息熵越大，事物越具有不确定性，信息熵的单位为 bit。

当两个变量之间存在相互作用时，我们可以通过观测其中一个变量来获知另外一个变量的部分信息，从而减少另一个变量的不确定性。所减少的不确定性大小可以用互信息来度量。例如，一个变量X原本服从这样的分布：X有0.5的概率取0，有0.5的概率取1。那么变量X的信息熵（不确定性）即为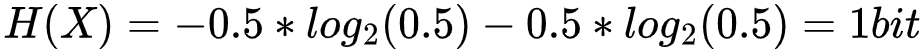。此时假设存在变量Y，Y和X存在相互作用，例如Y=X，当我们观测到Y的取值为1时，X的分布就变成了以1的概率取1，此时X不再具有任何不确定性，其熵变为 0 bit。这减少的1 bit信息是通过观测Y得来的，因此我们称减少的1 bit信息为互信息。

具体来说，互信息衡量的是通过观测Y能够给X减少的不确定性的大小。因此互信息的算法可以是用X原本的不确定性 H(X) 减去当Y被观测条件下的不确定性 H(X|Y)。使用这种思路，我们可以推导出互信息的计算公式为

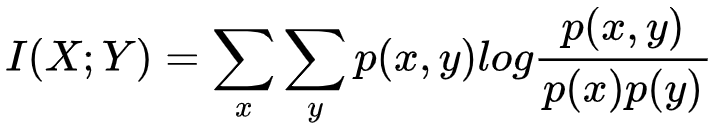
当相互作用的变量数量增多时，互信息的使用便会带来一定的问题，想象这样的场景：存在三个变量R₁, R₂, S，它们都以等概率取0或1，但彼此之间并不独立，其关系为：

R₁=R₂=S

如果我们观测到R₁，便能够确定S的取值，这一过程可以被互信息描述为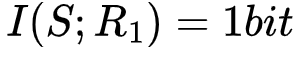。但如果我们提前知道了R₂的取值，那么在R₁被观测之前就知道了S的取值，即S的不确定性已经降为0，此时观测R₁已经不能S带来任何不确定性的降低。这种场景可以用条件互信息的语言来描述为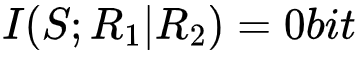，即在已知R₂的条件下，R₁的观测不能降低S的不确定性。在这一例子中，我们把R₁和R₂的位置互换，效果相同。

再考虑这样一个场景，同样是R₁, R₂, S三个以等概率取0或1的变量，它们之间的关系为：

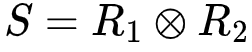（异或）

针对这一场景，在R₂未知的情况下，通过观测R₁，我们不能得到任何关于S的信息，即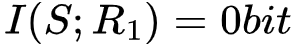，但如果R₂已知，我们即可通过观测R₁获得S的精确取值，即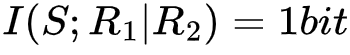，在这一例子中，我们把R₁和R₂的位置互换，效果相同。

在上述第一个例子中，R₁=R₂=S，我们单独观测R₁或R₂所获得的的信息量为1bit，在其中一个被观测后，再去观测另一个，就不再获得额外的信息量。此时我们可以说，R₁和R₂为S提供了一些冗余（redundant）信息。因为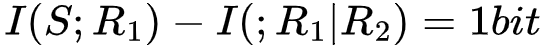，我们还可以知道它们提供的冗余信息量为1 bit。在上述第二个例子中，我们必须同时观测到R₁和R₂才能减少S的不确定性，此时我们可以说R₁和R₂为S提供了协同（syngernistic）信息。因为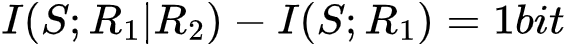，我们可以知道它们提供的协同信息量为1 bit。

但在所有情况下，冗余信息和协同信息都只能二者仅存其一吗？前文提到的冗余信息量的计算方法在更复杂的情况下仍然适用吗？在多变量作用于单变量的更复杂场景中，我们应该如何理解谁贡献了什么信息？这便是接下来要回答的问题。

三、多变量信息分解 

1. 计算冗余信息

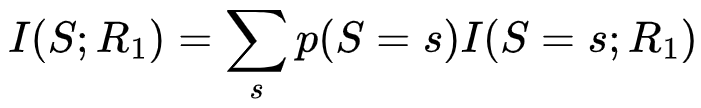
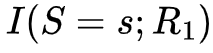其中表示了观测R₁对S取值为s这一事件的不确定性的减少，当然，观测R₂同样可能减少S取值为s的不确定性，我们取以上两个不确定性的最小值，即₁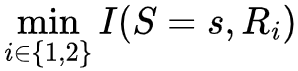，作为R₁和R₂关于S取s的冗余信息量。注意，这里指的是对S取值为s这一事件，R₁和R₂均可提供的信息量，因此这一信息量具有冗余的性质。进一步，冗余信息的期望可以被写成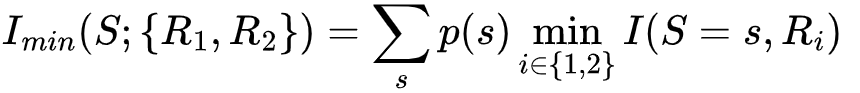

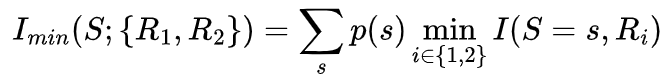
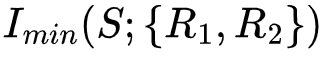在该系统中，容易知道目标变量S的熵为1 bit，从直观角度来理解该系统，我们会发现若R₁被观测，则S就没有任何不确定性了，S的熵降为0，即R₁为S提供了1 bit的信息，若R₂被观测，则我们也能完全知道S的取值，S所需的信息既被R₁提供又被R₂提供，则我们认为R₁和R₂为S提供了1 bit 的冗余信息。我们带入公可知，其计算结果也为1 bit，可见我们的直观分析是正确的。

冗余信息有如下三条重要的性质：

• 首先，冗余信息I_min应该是非负的，可以想象，如果任何源变量对目标变量的任何一个可能取值都无法贡献出公共信息，那么冗余信息即为0。
• 其次，冗余信息应该小于或等于任何一个源变量关于目标变量的互信息，我们可以从冗余信息的计算公式中分析出此性质：观察其计算公式，若针对S=s的每一个取值，A₀都比其他A_i提供了更少的信息，则此时 I_min（S；a）=I_min（S；A₀）。
• 另外，虽然我们通常定义冗余信息为多个源变量对目标变量提供的共同信息，但如果只有一个源变量，根据前述公式，我们仍然可以定义这个源变量为目标变量提供的冗余信息，实际上，经过计算，我们可以发现，这种冗余信息大小即为源变量和目标变量的互信息，即I_{min}(S; {A₁}) = I(S; A₁)。

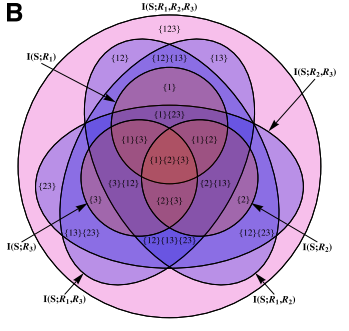
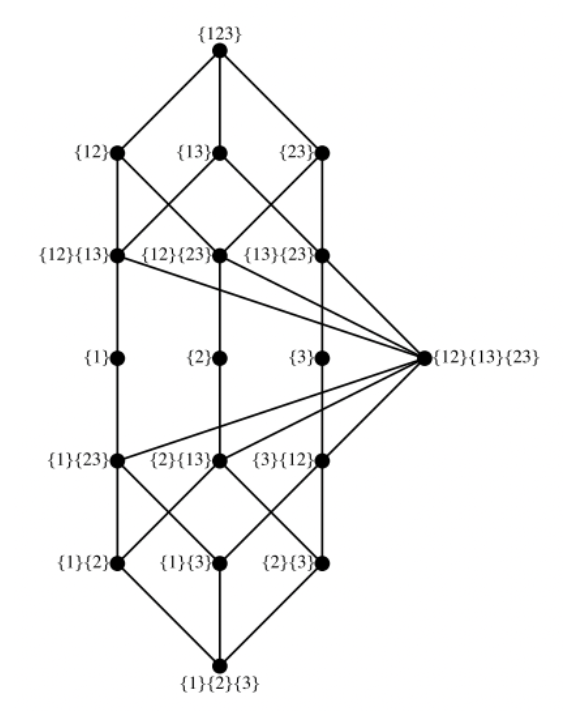
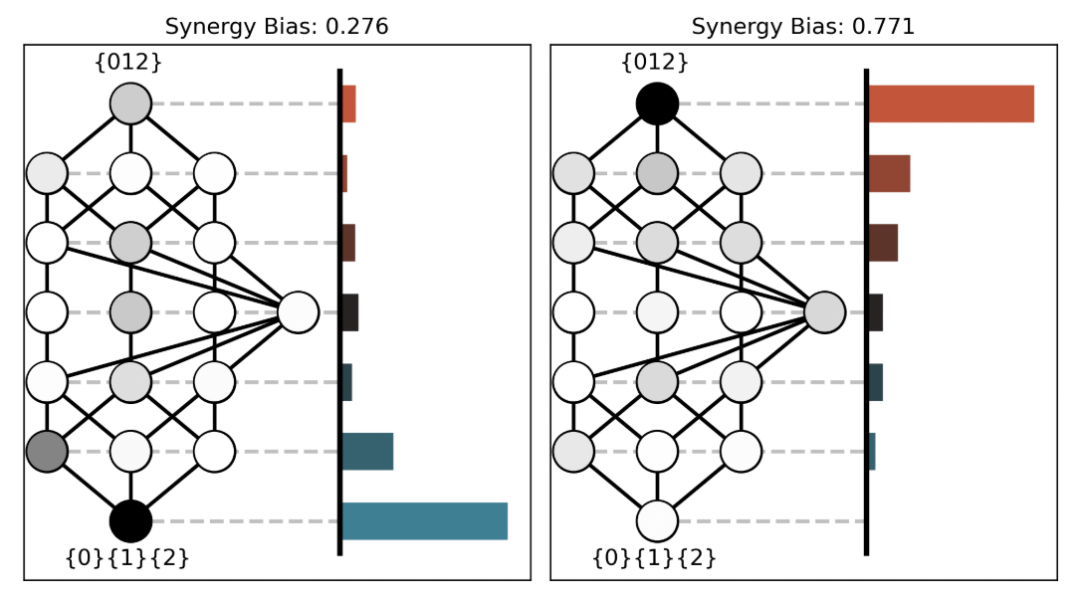
3. 冗余信息的结构

其中符号代表所有该节点的下层节点。

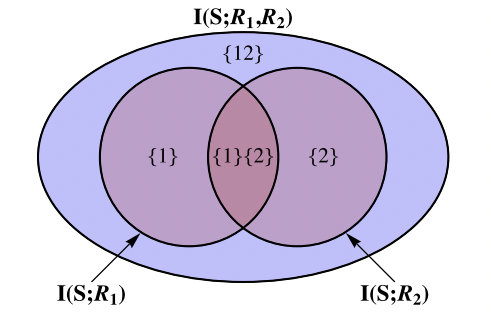
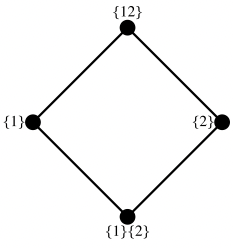
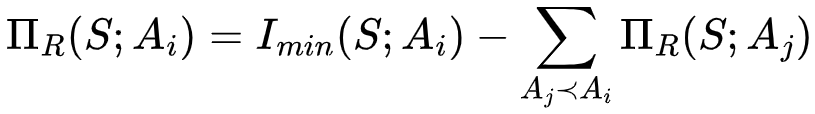
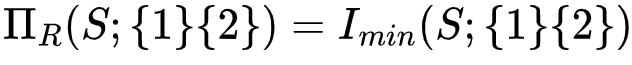我们以前文中的例子进行阐述：位于冗余晶格图上最底层节点{‍‍‍‍‍‍‍‍‍‍‍‍‍‍{‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍1}, {2}}由于没有任何下层节点，因此其信息分解结果即为该节点为目标节点提供的冗余信息量，即。而中间层的节点{1}的信息分解结果为该节点为目标节点提供的冗余信息量（即该节点和目标节点之间的互信息）减去底层节点的信息分解结果的值，即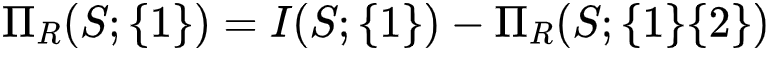。这一部分信息量由节点{1}单独提供，而不包括节点{1}和节点{2}提供的公共信息，因此我们将这一部分信息称之为单独（Unique）信息。

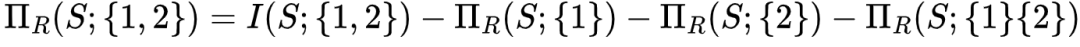通过这一方法，关于节点{1, 2}的信息分解结果即为，这表示仅有该节点，而非任何其余三个下层节点提供的冗余信息，具体来说，这也表示了通过联合观测节点{1}和{2}才能得到的信息，而非单独观测任何一个能得到，而观测另一个得不到的信息，也非节点{1}和{2}都可以为目标变量提供的信息。因此我们将这一信息称之为协同（Synergistic）信息。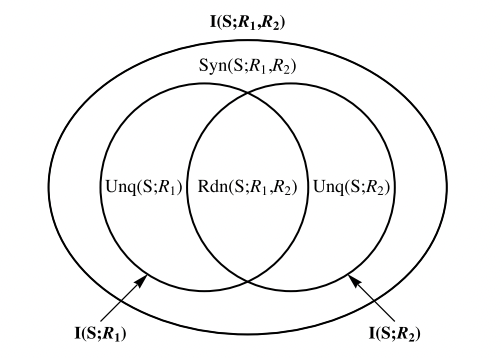

注意观察这张图，越上层的节点大体上对应越高尺度的变量或组合，越下层则是越低尺度的变量或组合，但这种信息分解和尺度以及粗粒化之间的对应关系并不是很明显，后续的文章也有更多的讨论。如果我们自下而上对每个节点的信息分解值进行累加，就得到了总的源到汇的互信息。如果自下而上地计算冗余信息I_min，则该数值会单调地增加，直到最上面的节点，I_min即是源到目标的总的互信息。如果自下而上对每个节点的信息分解值进行积分就得到了每个节点的I_min。

四、应用

 

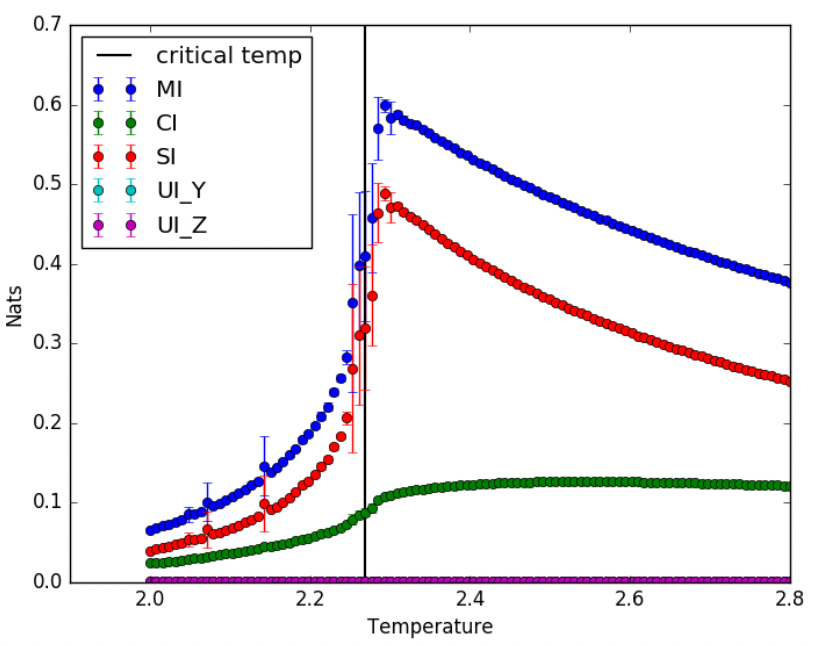
1. 信息分解方法在 Ising Model 中的应用

下图展示了作者将这一方法应用于二维 Ising Model 上的结果。值得说明的是，作者选取二维 Ising Model 中任意节点的四个邻居节点作为源变量，这一节点下一时刻的状态作为目标变量，用我们介绍的这一方法做了源变量关于目标变量的信息的分解。并研究了冗余信息、协同信息和单独信息随着系统温度变化的关系。

 

图6：Ising model 中不同类型的信息随温度的变化

 

在图6中，横坐标代表温度，其中黑线表示Ising model的临界温度，深蓝色的点代表一个节点的四个邻居与它下一时刻状态之间的互信息，红色的点代表分解而来的冗余信息，绿色的点则代表协同信息。根据上图我们可以发现，互信息和冗余信息都在临界温度附近达到了其最大值，在互信息中，冗余信息占据了很大的部分，而协同信息只占据了较小的部分，但随着模型逐渐向无序状态（温度升高）演化，协同信息量几乎保持不变，但冗余信息和互信息的量全部减小。因此，我们或许可以用信息分解的手段作衡量系统是否达到临界态。

 

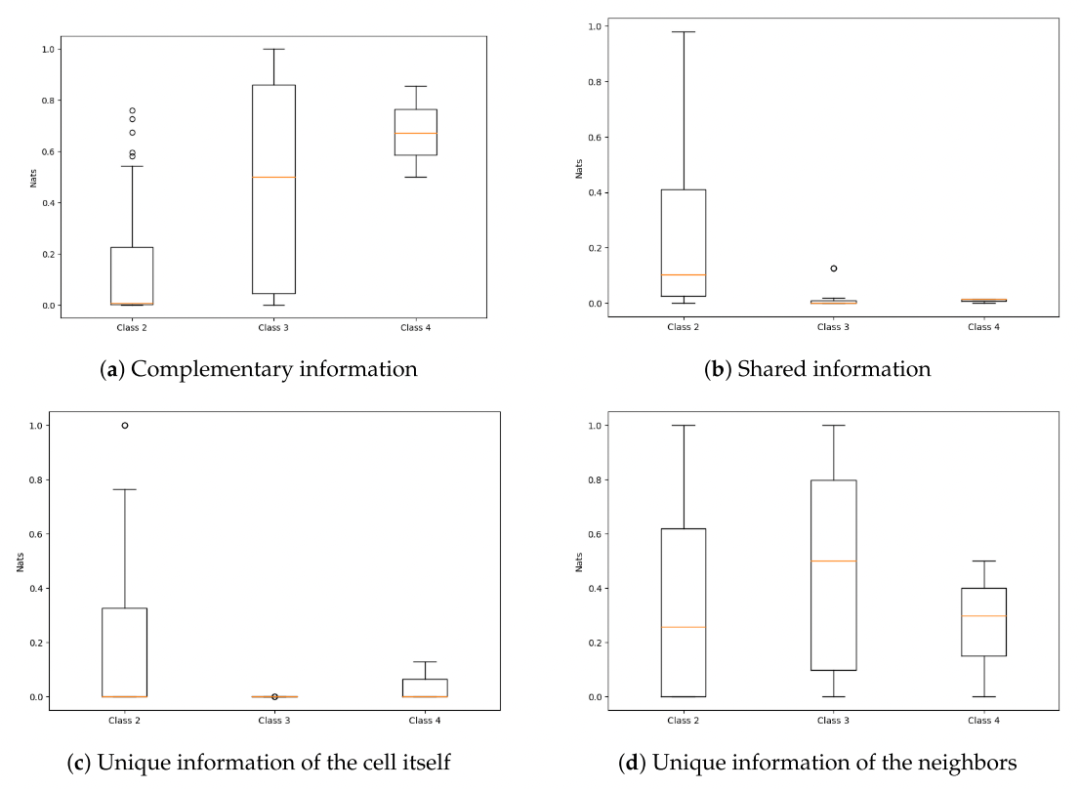
2. 信息分解方法在元胞自动机中的应用

作者还将这一方法应用于研究人员已经很熟悉的一维元胞自动机模型中。我们知道，在一维元胞自动机系统中，每个元胞的取值只能为0或1，它将受到它自己和左右邻居的影响，在未来时刻变化取值，因此共有256种二进制规则。Wolfram根据元胞自动机的演化模式将元胞自动机分为四种类型：

1. 元胞自动机很快演化为纯黑或纯白

2. 元胞自动机演化出周期性的、可重复的模式

3. 元胞自动机演化出混沌

4. 元胞自动机演化可以长时间存在的复杂斑图

 

在元胞自动机实验中，作者以一个元胞及其左右邻居状态作为源变量，这一元胞下一时刻状态作为目标变量，并使用信息分解方法，衡量了源变量之间的协同信息量、冗余信息量，以及元胞自己提供的单独信息量和其邻居提供的单独信息量。在图7中，作者对比了不同类型的元胞自动机中的信息分布。

 

图7：第二、三、四类元胞自动机中信息量的分布

 

根据图7（a），我们可以看到，从第二类，到第三类，第四类，随着元胞自动机的演化模式逐渐趋于复杂，其协同信息（在这里被称为Complementary Information）的量也在不断上升，这说明只有多个源变量高度协同时，才有可能产生复杂的斑图。在图7（b）中，我们看到，其冗余信息（在这里被称为Shared Information）只能在第二类元胞自动机中出现，这意味着若想要演化出混沌或复杂斑图，则源变量中不能出现具有大量冗余信息的情况。在图7（c）和7（d）中，作者对比了这一变量自己和邻居为自己未来提供的单独信息，并发现在混沌或复杂斑图中，邻居提供的单独信息遥远多于自己提供的单独信息。

 

作者还发现一个有趣现象，对于有一些元胞自动机来说，它们在宏观模式上是一致的，但在信息结构方面却迥然不同。如图8：

 

图8: 6号元胞自动机和130号元胞自动机

 

图8展示了两个宏观模式相似但信息结构却大相径庭的元胞自动机，分别是6号和130号。从宏观视角来看，它们的模式是类似的向左下方伸展的条纹，因此都被归类为第二类元胞自动机。但如果我们放大其微观结构，则会发现6号元胞自动机中出现了很多“倒L型区域”，而130号则没有，实际上6号形成“倒L型区域”是比较复杂的，需要多个源变量之间进行协同作用，而130号则不需要，这也解释了为什么两者在信息结构上有巨大的差距。

 

实际上，作者认为，信息分解方法可以作为Worfram对元胞自动机提出的分类的良好补充，Worfram提出的元胞自动机分类仅仅依赖于宏观模式和人的直觉，而并不依赖于信息论的基础。而使用信息分解的方法，我们可以对元胞自动机完成类似的分类，并更加注重元胞自动机微观的演化细节。

 

3. 信息分解方法在因果涌现中的应用

 

信息分解方法可以在总体上衡量一个系统的协同程度，这一功能使得信息分解方法也被用于因果涌现研究，在2020年公开于arXiv的文章“Emergence as the conversion of information: A unifying theory”中，因果涌现的提出者 Erik Hoel 就使用信息分解方法进一步定义了一个系统的协同程度，如图9：

图9：不同系统的协同程度

 

图9向我们展示了两个多变量作用系统，它们所描述的都是三个源变量作用于一个目标变量的情况。在两幅子图中，左边部分描述的是冗余信息晶格，而右边部分则描述了晶格中每一层携带的信息增量。在左图中，信息大多数由冗余信息提供，而右图中信息则大多由协同信息提供。因此，左图是一个冗余系统，右图则是一个协同系统。事实证明，对于类似左图中的信息结构，我们可以通过对其粗粒化增加这一系统的协同程度，进而产生因果涌现效应。

 

五、总结 

 

通过这篇文章，我们介绍了一种信息分解方法，该方法可以帮助我们清晰表述在多个源变量作用于一个目标变量的情况下的信息结构，可以回答一系列具体的问题，例如“谁为结果提供了多少信息？”，“它们为结果提供的信息中，有多少是互相冗余的？”，“有多少信息需要协同考虑多个变量才可以获得？”等等。我们首先定义了冗余信息（Redundant Information），然后通过分析冗余信息的性质，发现冗余信息天然存在着一种结构，进一步通过对冗余信息的分解，我们获得了单独信息（Unique Information）和协同信息（Synergistic Information）的定义和计算方法，从而帮助我们更好地理解了这一信息结构。

 

这篇文章的价值在于，它从某种程度上揭开了我们似乎已经很熟悉的“互信息”的神秘面纱，发明了一种类似“互信息的微积分”的方法，详细拆解了互信息的每一个元素应该如何理解和计算。这篇文章自发表以来便引起了科学家们的巨大兴趣，人们沿着这篇文章的方向进行了诸多探索，这些探索包括定义一些新的冗余信息计算方法，更深入地研究信息结构的性质，以及信息分解方法在不同领域中的应用等等。另一个有趣的现象是，这篇文章一直挂在arXiv上，从2010年至今也并未能正式发表，成为了一个另一个典型的无需杂志认可的经典文章案例。

 

我们还进一步介绍了这一方法在多种复杂系统中的应用，如Ising Model和元胞自动机这类已经被研究人员广泛研究的系统。我们也初步介绍了信息分解方法在因果涌现中的应用。

 

从信息流动的视角理解复杂系统，无疑可以增进我们对复杂性本质的理解。但本文所介绍的方法仍有一定的局限，例如，本文所介绍的方法只能适用于多变量作用于单变量的情况，但在一个复杂系统中，多变量之间存在着相互影响。又如，本文所介绍的方法计算复杂度非常高，导致该方法很难应用于源变量很多的情况，我们在「因果涌现读书会」第二季第二期解读了这篇文章，后面我们还会解读一些基于这篇文章开展的其他进展，这些进展在某种程度上克服了本文的缺点，为我们理解复杂系统提供了更多的工具，欢迎大家加入此次读书会，与我们共同讨论。

‍‍

本季读书会详情与报名方式请参考：

因果、涌现与机器学习：因果涌现读书会第二季启动

点击“阅读原文”，报名读书会