集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「集智斑图」推送论文信息。

扫描下方二维码，关注“集智斑图”服务号，即可订阅Complexity Express：           

 

Complexity Express 一周论文精选

以下是2022年8月8日-8月14日来自Complexity Express的复杂性科学论文精选。如果Complexity Express列表中有你感兴趣的论文，欢迎点赞推荐，我们会优先组织解读~

目录：

1. 面对大规模扰动事件时居民流动性的时空衰减模型

2. 高阈值限制网络合作中叛逃者回避的收益

3. 视觉皮层发育中的自发对称性破缺机制

4. 多尺度模式形成系统中的尺度桥接

5. 有影响力的科学家更倾向于与合作者参与新的课题

6. 通过神经网络中随机性和有序的数字计算

7. 将人与自然关系和人类福祉的非物质维度联系起来

8. 食品安全、营养与心理健康之间联系的系统性证据

1. 面对大规模扰动事件时

居民流动性的时空衰减模型

论文题目：A spatiotemporal decay model of human mobility when facing large-scale crises

论文来源：PNAS

论文链接：https://www.pnas.org/doi/10.1073/pnas.2203042119

流行病、山火和大风暴等大规模极端扰动事件的一个共同特征是，尽管它们在起因和持续时间上有所不同，但都能显著地改变人类的日常流动模式。这些变化在规模和持续时间因情况而异，既能影响扰动带来的后果，也会影响政府的响应能力。基于对美国9000多万人的自然跟踪和匿名移动行为，该研究记录了六次大规模扰动事件（如疾病、山火、风暴等）在空间与时间上的移动差异。研究建立了一个能有效地捕捉大规模极端扰动事件后人类移动性变化的高维异质性模型。从五个不同指标结果来看，无论空间尺度如何，人类流动性变化均呈现出一致的双曲线下降趋势，这种模式被研究者们称为“时空衰减”。

在新冠肺炎应用情景中，该模型还揭示了流动性变化的显著差异——来自高收入地区的居民不仅会在疫情爆发之初大幅度降低出行率，并且会长时间维持这一状态。来自低收入地区的居民表现出更快且更强的双曲线衰减趋势，研究者认为这可能有助于解释不同的新冠感染率。该模型能方便更好地理解和预测极端扰动事件后的居民的流动模式，从而帮助管理层提出更有效的应对措施。

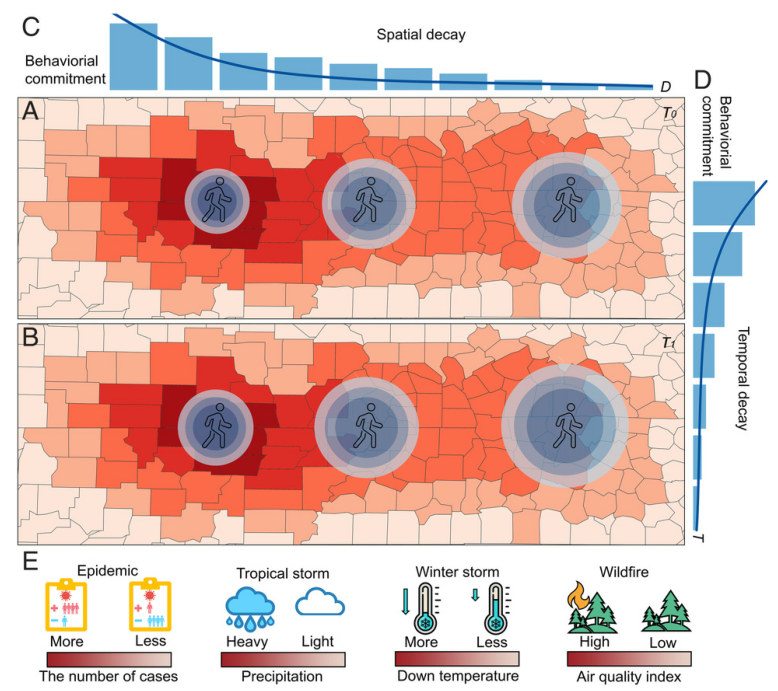
图：大规模极端扰动事件期间人类流动行为的时空衰退趋势。子图A和B分别反映扰动事件不同时期居民的流动行为。所有的居民都可能会减少他们的流动性，但程度不同。居住在扰动中心（深红色区域）的居民明显减少了出行，而居住在较远地区（浅红色区域）的居民则变化幅度较小。在不同的危机中，衡量危机的严重程度的标准各有不同。例如，在疫情情景中采用感染人数、大风暴期间用降雨量来反映。研究假设的衰变模式在空间维度（子图C）和时间维度（子图D）上表现出来。

2. 高阈值限制网络合作中

叛逃者回避的收益

论文题目：Sharp thresholds limit the benefit of defector avoidance in cooperation on networks

论文来源：PNAS

论文链接：https://www.pnas.org/doi/10.1073/pnas.2120120119

考虑一个由栖息地斑块组成的空间网络上的合作博弈，如果参与者判断当地条件不利，他们可以在斑块之间重新定位。随着时间的推移，迁移事件可能会导致同质状态，其中所有斑块都具有相同的合作者和叛逃者（cooperator and defector）的相对密度，或者它们可能会导致自组织模式，其中一些斑块成为安全避风港，保持较高的合作者密度。本文从数学上分析这些状态之间的转变。研究发现，一旦超过一定的连接度阈值，就会形成安全避风港。这一阈值可以解析地与斑块网络的结构相联系，并且具体地与某些网络基序相联系。令人惊讶的是，宽恕的叛逃者回避策略可能对合作者最有利。研究结果表明，生态元社区模型（ecological metacommunity model）中的合作博弈分析在数学上是容易处理的，并有可能将宏观生态模式、行为演化和网络拓扑等主题联系起来。

具体而言，作者研究了一个受生态元群落启发的空间结构种群中的合作模型，其中网络节点并非个体而是代表包含个体间许多相互作用的栖息地斑块，边表示两个斑块通过这些个体的扩散连接在一起（图1A）。每个斑块是博弈的地方，窝藏着合作者和叛逃者子群，由于内部互动和地点之间的移动，他们会随着时间的推移而增长和缩小。元群落模型使人们能够直接和明确地表示物理空间结构的影响。此外，可以使用主稳定函数对它们进行分析，这些函数可以用来理清局部动力学和网络结构的影响。作者利用这一能力来探索不同的移动策略如何影响作为网络结构函数的合作博弈的结果。

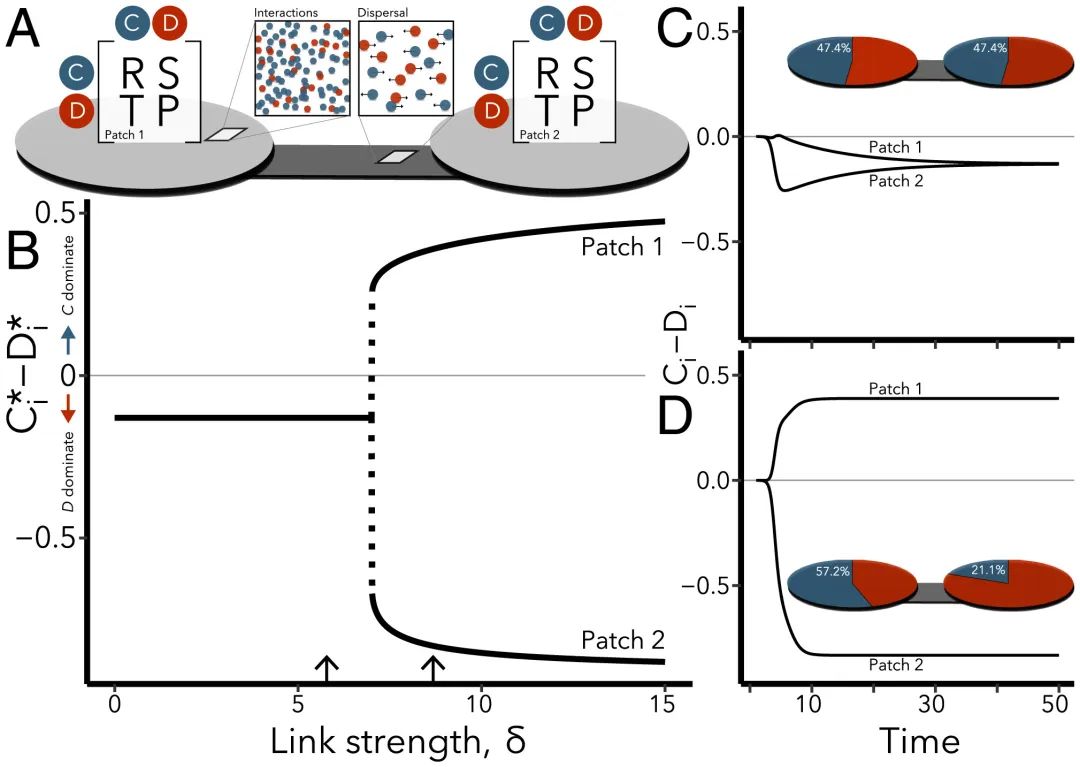
图：两片网络上异质定态的出现。(A) 空间博弈示意图，显示合作者和叛逃者之间的局部回报（Π）关系（灰色圆圈）以及他们之间的扩散路线。(B) 随着链接强度的变化，斑块1和2中两种类型的平衡密度差异。箭头指的是C和D中所示的示例时间序列。初始条件的取值范围是[10^-4，10⁻³]，初始合子密度最大的是斑块1。(C) 均匀稳态，C和D在不同位置具有相同的平衡密度。（嵌入图）显示每种类型在每个嵌块中的比例图。(D) 相同的博弈，但扩散速度更快（更大的δ），显示出在斑块1中出现了具有更高合作者密度的异质稳态。参数为 R=3，S=2，T=5，P=0.2，μ=1，α=3。

3. 视觉皮层发育中的

自发对称性破缺机制

论文题目：Mechanisms for Spontaneous Symmetry Breaking in Developing Visual Cortex

论文来源：Physical Review X

论文链接：https://journals.aps.org/prx/abstract/10.1103/PhysRevX.12.031024

大脑为了能够识别出图片中的局部方向，神经元必须自发打破它们响应函数的平移以及旋转对称性，这是无监督学习的典型例子。在生物学中无监督学习的主要框架是Hebb原理，然而Hebbian学习如何打破这种对称性是一个长期存在的生物物理谜题。理论研究认为，这需要输入到视觉皮层，以逆转它们在远距离上相关性的相对大小。经验测量徒劳地寻找这样的倒置，并报告相反的情况是正确的。

本文正式地通过多层模型的厄米化来解决这个问题，这将它映射到一个零温度相变问题。在新的相图中，只要 (i) 循环相互作用的范围足够长，(ii) Hebbian竞争被适当考虑，这两种对称性就会自发地打破。对称性破缺的一个关键因素是来自同一传入细胞的连接之间的竞争。这样的竞争，加上输入相关性随着距离的简单单调衰减，能够触发图像处理所需的破缺对称相位。作者分析预测了使得这种新机制得以出现的相关长度尺度的相对幅度。这些结果使得实验观察符合 Hebbian 范式，揭示了视觉皮层发育的新机制，并有助于我们对学习和对称破缺之间关系的理解。

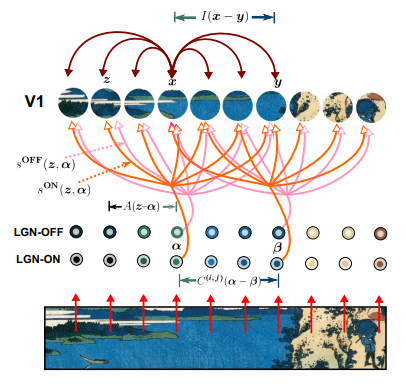
图：模型示意图。初级视觉皮层（Primary visual cortex, V1）是大脑皮层接收视觉感觉信息的第一个区域。上面一行较大的圆圈表示的是单一的突触后细胞层。输入V1的信号来自丘脑外侧膝状核（LGN）， LGN依次接收来自眼睛的信号。

4. 多尺度模式

形成系统中的尺度桥接

论文题目：Bridging scales in a multiscale pattern-forming system

论文来源：PNAS

论文链接：https://www.pnas.org/doi/10.1073/pnas.2206888119

自组织模式的形成对许多生物过程至关重要。反应扩散模型（Reaction–diffusion model）让我们更深入地理解，生物系统如何从同质化开始，发展出空间结构。然而，生物过程本质上涉及多个空间和时间尺度，并随时间从一种模式转变为另一种模式，而不是从同质化到一种模式。为了处理这样的多尺度系统，需要粗粒化方法将动力学约减到大尺度上的相关自由度，但不丢失小尺度上关于模式的信息。

本文提出一种半现象学方法，利用模式形成中的质量守恒（mass conservation），并使得从大尺度动力学重建关于模式的信息成为可能。其基本思想是划分不同区域（粗粒度），并确定每个区域的瞬时色散关系，这最终会表明局部模式形成的不稳定性。作者们通过研究蛋白质模式形成的聚合模型“Min系统”来说明该方法。研究通过模拟首先表明，Min系统在一种空间异质性几何中产生多尺度模式。这一预测被Min系统的体外重建实验证实。利用最近发展的质量守恒反应-扩散系统理论框架，研究表明，总蛋白质密度在大尺度上的时空演化可靠地预测了模式形成动力学。该方法为分析粗粒度方法不适用的复杂系统提供了一个替代和通用的理论框架，原则上可以应用于具有底层守恒定律的广泛系统。

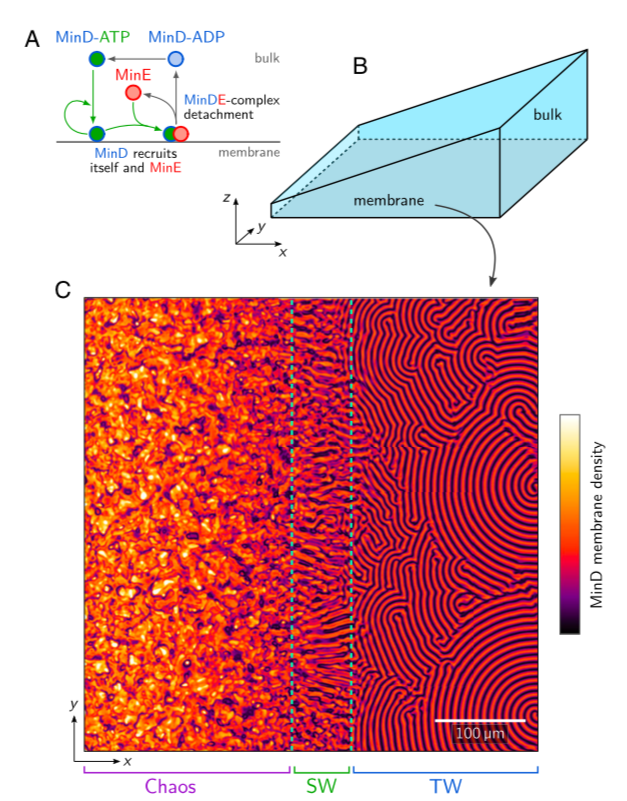
图：(A) Min蛋白反应网络示意图。(B) 楔形几何结构，底面（z = 0）为膜表面，体高H(x)沿x方向线性增加。(C) MinD 的膜密度快照，通过数值模拟如图B所示的几何形状的 Min 动力学得到。沿着膜和不同体高，可以观察到混沌模式（Chaos）、驻波（SW，绿色）和行波（TW）区域。

5. 有影响力的科学家

更倾向于与合作者参与新的课题

论文题目：Impactful scientists have higher tendency to involve collaborators in new topics

论文来源：PNAS

论文链接：https://www.pnas.org/doi/10.1073/pnas.2207436119

在科学研究中，合作是利用新思想、新技能和多种资源进行跨学科研究的最有效的方式之一。尽管在过去科研合作网络已被深入研究，但是关于科学家个体如何选择合作者来开展新课题的问题几乎没有被探索过。此项研究收集了个体科学家职业生涯中的合作统计数据和机制信息，一般来说，合作者涉及的主题比代理人预期的要少得多。研究发现高产科学家倾向于拥有更多的单主题合作者，而高被引（有影响力）的科学家拥有更多的多主题合作者，基于该发现研究还提出了产生这一区别的潜在机制。此外，研究者们还调查了科学家让现有合作者继续参与新课题的案例。结果表明，与高产科学家相比，有影响力的科学家更倾向于与高影响力的科学家在新课题上合作。研究者们也通过调查不同年份和不同学科的活跃科学家来验证以上发现。

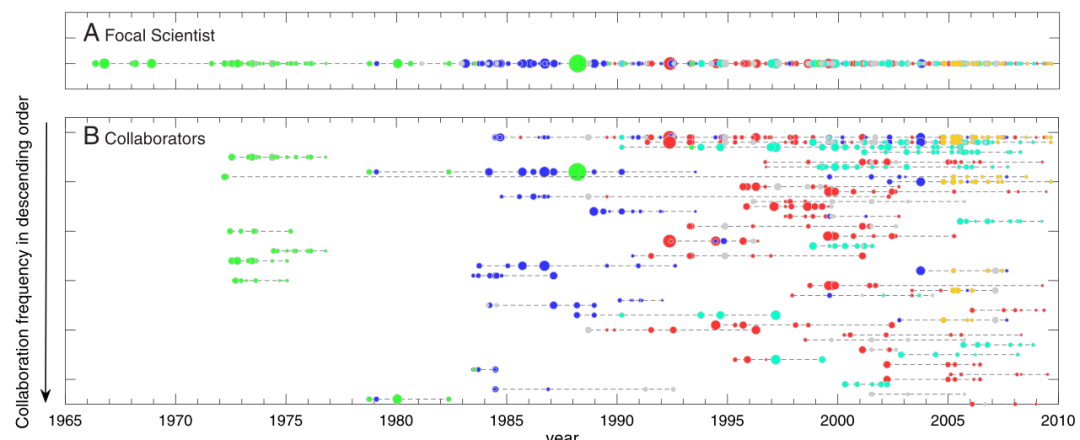
图：科学家的合作者所涉及的主题说明示意图。A显示了一个焦点科学家职业生涯中研究主题的演变。每个节点都是这位科学家发表的论文，节点的颜色代表了这些论文的研究主题。节点大小代表论文的引用次数。B显示了这位焦点科学家的合作者参与的研究主题。合作者按照与焦点科学家合作的论文数量从上到下降序排列。每一行显示一个合作者的成果，上面的每个节点代表一个与焦点科学家合作的论文。

6. 通过神经网络中

随机性和有序的数字计算

论文题目：Digital computing through randomness and order in neural networks

论文来源：PNAS

论文链接：https://www.pnas.org/doi/10.1073/pnas.2115335119

本文提出，大脑中的编码、解码是通过数字计算实现的，通过三个原理：输入的相对序数编码，神经元之间的随机连接，信念投票。由于随机化和相对编码的粗粒化，作者向我们展示对于编码、解码序列的无错误重建，这些原理是完全充分的。特别是，随着输入库的大小呈指数增长，所需的神经元数量线性增长。作者通过重建序列来说明模型，序列包含十亿项目的库。

由此，作者推导出神经元集群中学习和传递信息能力极限的香农方程，然后推广到任何类型的神经网络。根据有效编码的最大熵原理，表明随机连接可以将输入信号中的冗余信息去相关，为神经元创建更紧凑的编码，从而传递更大量的信息。因此，尽管相对编码不可靠，但很少有神经元需要对原始信号进行无错误的区分。最后，作者讨论了这一数字模型在大脑神经生物学发现方面的意义，以及人工智能算法、神经信息理论、数字神经网络设计方面的意义。

图：基于随机排列序数编码的神经集群示意图。这个过程有三个阶段：原始序列的编码、解码和全局信念投票。

7. 将人与自然关系和

人类福祉的非物质维度联系起来

论文题目：Linking the nonmaterial dimensions of human-nature relations and human well-being through cultural ecosystem services

论文来源：Science Advances

论文链接：https://www.science.org/doi/10.1126/sciadv.abn8042

大自然通过其多样的物质和非物质贡献为人类幸福感做出了重大贡献。然而，尽管关于非物质层面的人与自然关系的文献越来越多，但我们缺乏对自然是如何与人类幸福感相联系的系统理解。本文使用文化生态系统服务（cultural ecosystem services, CESs）的概念作为探索该问题的视角。通过系统综述的经过同行评议的论文，我们得出了连接个体文化生态系统服务和人类幸福感各个组成部分的独特方式和机制，并判别各个组成部分的相对影响。随后，我们通过潜在类分析和多重对应分析，来识别它们之间的复杂相互作用，这些分析描述了文化生态系统服务与人类幸福感之间的协同作用和权衡的五种组分。我们批判性地讨论关键的研究趋势和（研究与应用的）差距，并为未来的研究和实践提出方向，以便更广泛地发挥大自然可持续地提升人类幸福感的潜力。

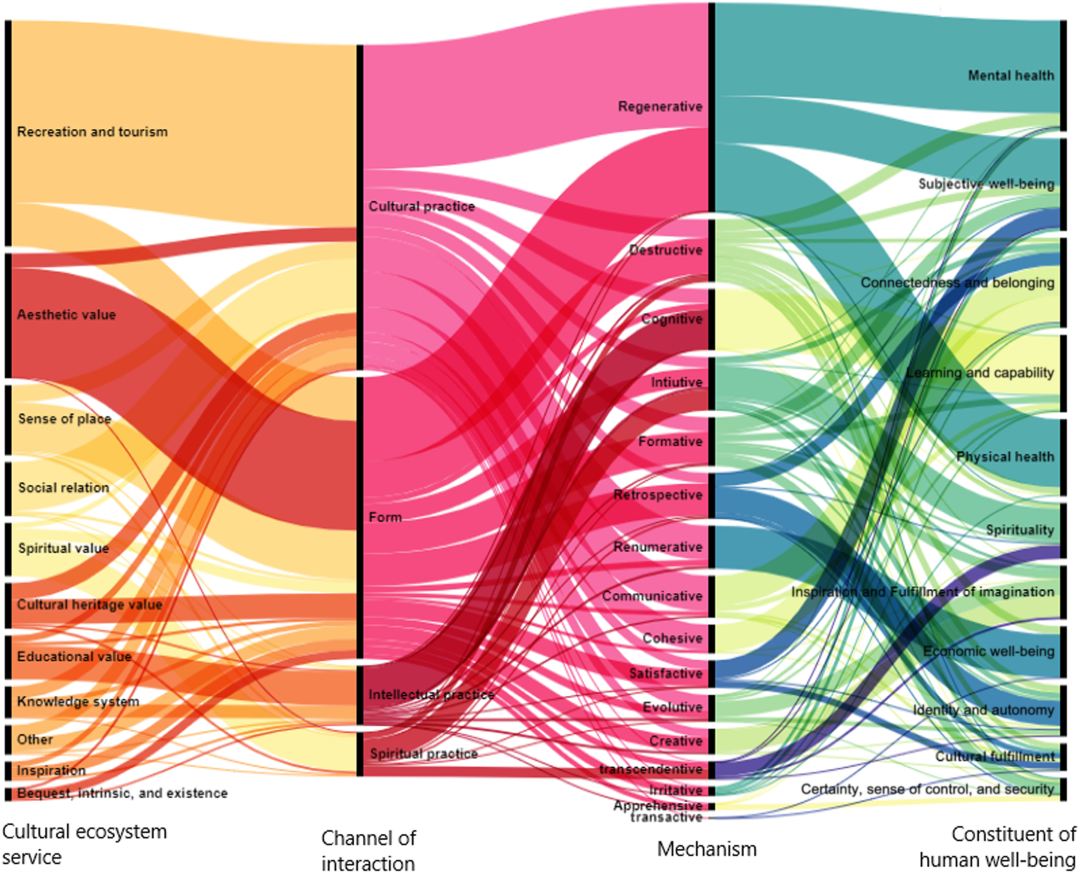
图：在综述文章中，提到的自然生态系统服务发挥作用的方式、机制以及对人类幸福感不同组成部分的频率。连接冲积图中任意两个元素的每条线的宽度代表相关观测的数量（包含1114个独立研究）。线的粗细基本上反映了文献中每个要素的受欢迎程度/可见度，不应被视为将任何两个要素联系在一起的重要性或权重。

8. 食品安全、营养

与心理健康之间联系的系统性证据

论文题目：Systematic evidence and gap map of research linking food security and nutrition to mental health

论文来源：Nature Communications

论文链接：https://www.nature.com/articles/s41467-022-32116-3

食品安全和营养与心理健康之间的联系已经获得了分析研究，但鉴于文献的广度，很难得出结论。此外，对于继续研究几乎没有指导意见。我们搜索了三个数据库，对食品安全及营养与心理健康之间的联系进行分析研究。在30,896个文献中，我们将1945个研究的特点映射到一个交互式的证据和差距图（EGM）上。在这些研究中，生理测量指标（尤其是 BMI）和饮食与心理健康（主要是抑郁症）的关系最为密切。关于婴幼儿喂养、出生方式与焦虑、压力和心理健康相关的营养生物标志物的研究较少。三分之二的研究假设，对食品安全和营养的测量值是会影响心理健康结果的因素。大多数研究是观察性的，次多的研究类型是系统评价。三分之一的研究是在中低收入国家进行的。这张地图对相关研究（食品安全和营养与心理健康之间的联系）的范围和性质进行了可视化分析，可能会指导未来研究的有用建议。

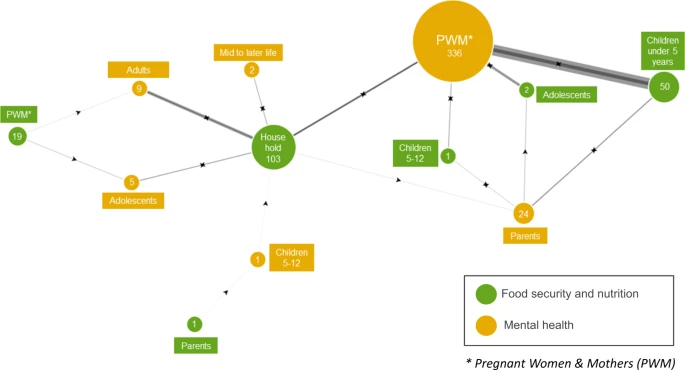
图：研究的网络图显示了一个人群中食品安全和营养，与另一个人群中心理健康之间通过假设关系方向的研究关系频率。点的大小和它们之间的连边的宽度根据研究的数量和文献中假设关系的频率进行调整。根据研究，箭头的方向表示假设的效应方向，相反方向的双箭头表示两个方向在不同的研究中已被假设。

关于Complexity Express

Complex World, Simple Rules.

复杂世界，简单规则。

由于学科交叉融合，大量针对复杂系统的研究成果散落在人工智能、统计物理、网络科学、数据科学、计算社会科学、生命科学、认知科学等等不同领域的期刊会议中，缺乏整合。

 

为了让大家能及时把握复杂系统领域重要的研究进展，我们隆重推出「Complexity Express」服务，汇总复杂系统相关的最新顶刊论文。

 

Complexity Express 是什么？

Complexity Express 每天爬取复杂系统领域最新发表的顶刊论文，每周通过“集智斑图”服务号汇总推送。

 

进入 Complexity Express 页面即可随时查看顶刊论文更新，你也可以通过微信接收研究更新推送和一周汇总。

               

Complexity Express 为谁服务？

• 如果你是复杂系统领域的研究者，可获得重要论文上线通知，每周获取最新顶刊论文汇总。

• 如果你是复杂系统领域的学习者，可了解学界关注的前沿问题，把握专业发展脉络。

• 如果你是传统的生命科学、社会科学等学科中的研究者/学习者，可以从复杂科学和跨学科研究中获得灵感启发。

• 如果你是关注前沿研究发现的知识猎手，可获得复杂系统研究对自然和人类世界的最新洞见。

Complexity Express 栏目也是集智俱乐部公众号的主要选题来源，诚挚邀请你订阅，与我们信息同步。

 

Complexity Express 论文从哪里来？

考虑复杂系统研究往往属于跨学科工作，我们主要抓取综合类和泛物理类/计算机类的顶级期刊，从每周新发表的数百篇论文中精选出与复杂系统相关的论文。

 

Complexity Express 参考影响因子和学者口碑，选择了如下期刊，每日爬取其论文更新：

• Nature

• Science

• PNAS

• Nature Communications

• Science Advances

• Physics Reports

• Physical Review Letters

• Physical Review X

• Nature Physics

• Nature Human Behaviour

• Nature Machine Intelligence

• Review of Modern Physics
• Nature Review Physics
• Nature Computational Science
• National Science Review
• 更多期刊持续增补中，欢迎推荐你认为重要的期刊！

 

如果你在 Complexity Express 中发现了感兴趣的论文，请立刻“点赞”！每周最高赞的论文，集智编辑部将组织专业解读~

 

Complexity Express 追踪哪些领域？

我们力求兼顾热点追踪与领域覆盖，目前筛选的论文主要集中在如下与复杂性关系密切的领域：

• 复杂系统基本理论
• 复杂网络方法及应用
• 图网络与深度学习
• 计算机建模与仿真
• 统计物理与复杂系统
• 量子计算与量子信息
• 生态系统、进化、生物物理等
• 系统生物学与合成生物学
• 计算神经科学与认知神经科学
• 计算社会科学与社会经济复杂系统
• 城市科学与人类行为
• 科学学
• 计算流行病学
• 以及一些领域小众，但有趣的工作

 

由于复杂性研究领域横跨多个学科，研究论文散落在不同的期刊上，很难不重不漏地把握最新工作。针对复杂性领域的论文筛选，我们专门设计了算法。经过数月的训练迭代优化，目前对上述领域爬取准确率达到90%以上。

 

将来我们还会根据你的具体研究领域，推出研究分类与个性化的订阅服务，敬请期待！

 

由于复杂性领域涉及的论文关键词和研究问题纷繁复杂，所以算法难免有不成熟的地方，如果你发现我们有漏掉的重要论文，或者爬到了领域有偏差的论文，欢迎联系我们（小助手微信：swarmaAI），帮助我们持续优化算法。

如果你对科学学、计算术语学等感兴趣并有代码能力，欢迎报名成为集智算法志愿者/实习生（具体请邮件联系算法组负责人huqiao@swarma.org）。

如果你对复杂科学及相关跨学科研究有长期兴趣，并乐于解读分享，欢迎加入集智作者团队（具体请邮件联系编辑部负责人liupeiyuan@swarma.org）。

更多论文

更多复杂性顶刊论文，请到Complexity Express页面查看。订阅即可每周获取更新提醒。

       

点击“阅读原文”，追踪复杂科学顶刊论文