集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「集智斑图」推送论文信息。

扫描下方二维码，关注“集智斑图”服务号，即可订阅Complexity Express：           

 

Complexity Express 一周论文精选

以下是2022年9月5日-9月11日来自Complexity Express的复杂性科学论文精选。如果Complexity Express列表中有你感兴趣的论文，欢迎点赞推荐，我们会优先组织解读~

目录：

1.  分解相互作用系统中的局部时间之箭

2. 时间信号驱动多细胞信息网络的涌现

3. 神经计算的几何学统一了工作记忆和计划

4. 基本网络模体对扰动集体响应的影响

5. 有损电网振荡器模型的多稳定性与异常

6. 中国城市人口老龄化、代际转换与能源消耗 

7. 破碎景观中的多物种共存

8. 超光速信号在闵可夫斯基时空中的不可能性并不排除因果循环 

1.分解相互作用系统中的

局部时间之箭

论文题目：Decomposing the Local Arrow of Time in Interacting Systems

论文来源：Physical Review Letters

论文链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.129.118101

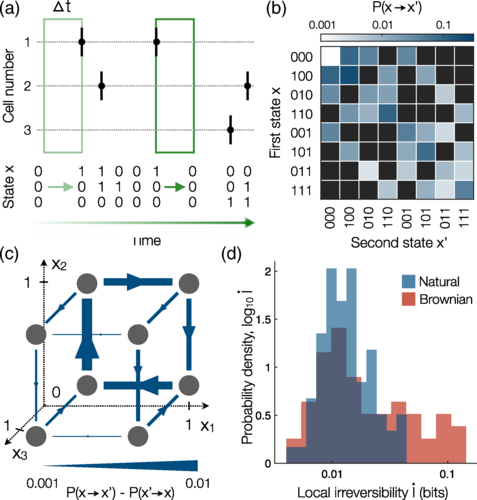
研究人员提出了一个局部时间之箭可以分解的证据，局部时间之箭相当于热力学系统中的熵增。在一个具有多个自由度的系统中，有一个项源于单个变量的不可逆动力学，然后是一系列由变量对、三元组和高阶组合项之间的相关性贡献的非负项。研究人员在噪声逻辑计算的简单模型上说明了这种分解，并将其应用于视网膜神经活动模式的分析，因为它可以响应复杂的动态视觉场景。研究人员发现，即使没有视觉输入，神经活动也会打破细致平衡，这种不可逆性主要来自神经元对之间的相互作用。

图：神经元的局部不可逆性。（a-c）蝾螈视网膜上的一组三个神经元对自然影像做出反应。(a）点标记三个神经元中每个神经元的动作电位次数；（b）8 种不同状态的分布函数；（c）不同状态之间的概率流；（d）对自然电影（蓝色）或布朗刺激（红色）作出反应的 5 个细胞群的局部不可逆性分布概率。

2.时间信号

驱动多细胞信息网络的涌现

论文题目：Temporal signals drive the emergence of multicellular information networks

论文来源：PNAS

论文链接：https://www.pnas.org/doi/10.1073/pnas.2202204119

环境刺激的协调反应对于多细胞生物体来说至关重要。为了克服细胞间的异质性和单个细胞内的噪声信号动力学的障碍，细胞必须与同伴有效地交换信息。然而，人们对由外部信号驱动的集体信息传递的动力学和机制知之甚少。在这里，我们研究了在微流控装置中形成汇合单层并对循环 ATP 刺激做出反应的神经元细胞的钙离子动力学。使用格兰杰推理来重建细胞之间的潜在因果关系，我们发现细胞自组织成空间分散和时序静态的网络，以支持通过间隙连接通道的信息传递。因果网络的连通性取决于外部刺激的时间分布，其中短周期或具有小占空比的长周期会导致连通性降低和网络拓扑结构破裂。我们建立了一个基于可通信的兴奋单元的理论模型，该模型再现了我们的观察。该模型进一步预测，因果网络的连通性在最佳通信强度下是最大的，这一点在实验中得到了证实。我们的研究结果表明，神经元细胞之间的信息传递是由刺激的时间分布进行外部调节，并由细胞间的信息传递进行内部调节。

图：由循环 ATP 刺激驱动的多细胞网络的动力学演变。（A）一个多细胞网络的例子在两个连续的周期之间重连接。三种类型的重连接事件由其各自的速率（每周期的概率）决定：移除一条边（Pdel)，增加一条新边（Padd)，以及翻转现有边的方向（Pflp）。（B）在不同的驱动周期 T 下移除、增加和翻转边的速率。青色表示 T=20 秒，品色表示 T=120秒，黄色表示 T=200 秒。（C）散点图显示连续周期之间增加的（Eadd）和移除的（Edel）边的数量，并以最近邻的总数（Etot）为标准。不同的符号代表 ATP 浓度。圆形表示 10μM，三角形表示 50μM，倒三角表示100μM。

3.神经计算的几何学

统一工作记忆和计划

论文题目：Geometry of neural computation unifies working memory and planning

论文来源：PNAS

论文链接：https://www.pnas.org/doi/10.1073/pnas.2115610119

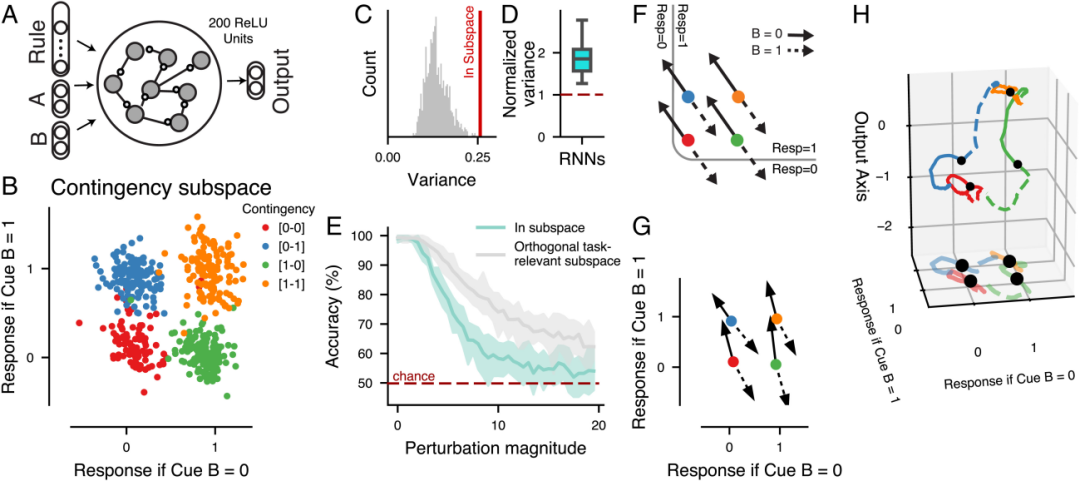
现实世界的任务需要工作记忆、决策和计划的协调，但这些认知功能被不成比例地作为大脑中独立的模块过程来研究。在此，我们提出权变表征（contingency representation），定义为未来行为如何依赖于即将发生的事件的映射，可以统一工作记忆和计划计算。我们设计了一个能够区分不同类型表征的任务。在任务优化的循环神经网络中，我们研究了权变表征的可能电路机制，发现这些表征可以解释工作记忆任务中来自前额叶皮层的神经生理学观察。我们的实验表明，人类行为与权变表征相一致，而不是与工作记忆的传统感官模型相一致。最后，我们对神经数据生成了可证实的预测，以确定神经数据中的权变表征，并将不同的工作记忆模型分离出来。我们的研究结果描述了一种神经表征策略，它可以将工作记忆、计划和依赖环境的决策统一起来。

图：CDL 训练的 RNN 的功能权变子空间。（A）RNN 模型的结构示意图。隐藏层由 200 个全连接的 ReLU 神经元组成。（B）我们通过对晚期延迟期的单元状态进行线性回归，定义了一个权变子空间，以确定“对 B=0 的反应”和“对 B=1 的反应”所沿的两个轴。（C）比较权变子空间与随机二维任务相关子空间的变异量互换试验。（D）对 20 个随机初始化的 RNN 复制了 B 中的分析，并绘制了与同等维度的随机任务相关子空间的平均方差相比，权变子空间所捕获的方差分布。（E）扰动分析的平均 CDL 性能（准确性），其中 RNN 状态在线索 B 开始前的时间点被一个给定规范的随机矢量扰动，该随机矢量可以在权变子空间（青色线）或正交任务相关子空间（灰色线）中。扰动幅度，即扰动的常数，是依次增加的。阴影区域代表重复 RNNs 的 SEMs。红色虚线代表权变行为。（F）利用权变表征的 CDL 反应选择的理论示意图。实线箭头代表由线索 B=0 引起的轨迹，虚线箭头代表由线索 B=1 引起的轨迹。非线性分离矩阵边界（灰色）划分了状态空间的区域，网络将从这些区域过渡到 0 或 1 的反应状态。（G）RNN 模型的平均权变子空间轨迹，从线索 B 的开始到偏移，轨迹被权变和线索 B 划分。x 轴和 y 轴代表权变子空间，而 z 轴是 RNN 模型的输出轴。

4.基本网络模体

对扰动集体响应的影响

论文题目：Impact of basic network motifs on the collective response to perturbations

论文来源：Nature Communications

论文链接：https://www.nature.com/articles/s41467-022-32913-w

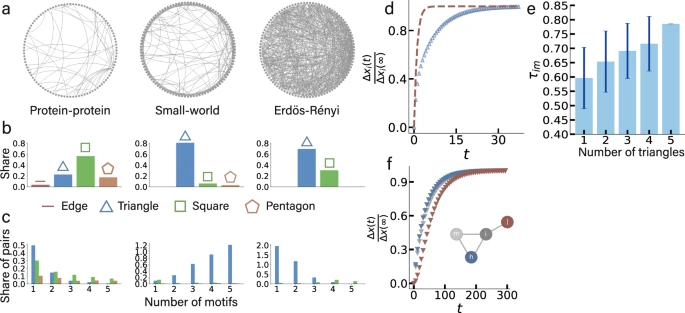
许多集体现象，如网络上的社会经济系统中的流行病传播和级联故障，都是由动力学的扰动引起的。扰动如何在网络中传播、影响和破坏其功能，可能取决于网络、扰动的类型和位置以及传播的动力学。以前的工作分析了传播路径上的节点的延缓效应，提出了一些瞬时传播的“标度”机制，作为网络节点度的函数，但没有考虑三角形等模体（motif） 的情况。然而，经验性网络包括使系统正常运行的模体。在这里，我们表明，传播路径上的基本模体共同决定了以前提出的距离限制传播和度数限制传播的标度机制，甚至停止了它们的存在。我们的结果表明，这些标度制度有一个根本性的偏离，并提供了对自动力学、相互作用动力学和拓扑学特性的相互作用的更深入的理解。

图：随机网络中模体传播动力学的影响。（a）从左到右：蛋白质-蛋白质网络、小世界网络、 Erdös-Rényi（ER）网络。（b）网络的模体份额（边、三角形、正方形、五边形）。（c）作为基本模体（三角形、正方形、五边形）一部分的边的数量。该份额是由作为相应模体一部分的边的数量除以网络大小计算的。（d）作为（独立）边的一部分的目标节点 i（棕色）比作为三角形一部分的其他目标节点 i（蓝色）反应更快。（e）从随机选择的源到其随机选择的相邻目标节点的平均传播时间直方图，是三角形数量（1-5）的函数。（f）扰动响应的四节点网络模型，目标节点 i 及其邻居 j 和 h，对源 m 的扰动。

5.有损电网振荡器模型的

多稳定性与异常

论文题目：Multistability and anomalies in oscillator models of lossy power grids

论文来源：Nature Communications

论文链接：https://www.nature.com/articles/s41467-022-32931-8

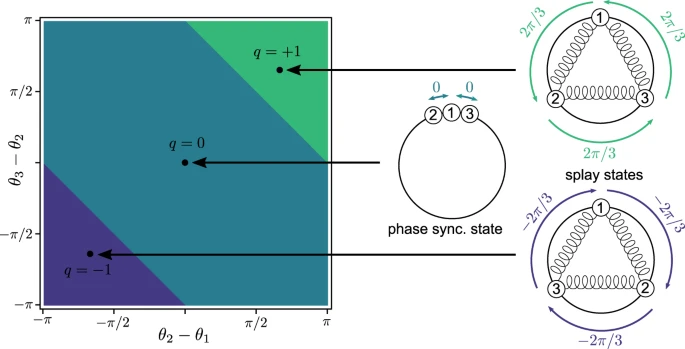
耗散耦合振荡器的分析在电网中具有挑战性和高度相关性。由于耗散耦合引起的网络对称性缺乏，标准数学方法并不适用。近期，研究人员展示了耗散耦合振荡器中的稳定同步状态与其状态空间的绕组分区之间的密切对应关系，这是由网络拓扑引起的几何概念。利用这种绕组分区，研究人员设计算法来计算耗散耦合振荡器的复杂网络的所有同步解决方案。这些几何和计算工具使研究人员能够识别有损网络系统的异常行为。与直觉相反，结果表明，循环流动和耗散可以增加系统的传输能力，并且耗散可以促进多稳定性。研究人员应用构建的几何框架来计算 IEEE RTS-96 测试系统上的功率流，并确定了两个具有不同回路流的高压解决方案。

图：3-环面的投影绕组单元分区（左）和弹簧网络的三个平衡的表示（右）。左侧面板中的彩色区域表示具有相同绕组数的点集，即绕组单元，形成 3-环面的分区。

6.中国城市人口老龄化、代际转换

与能源消耗

论文题目：Aging, generational shifts, and energy consumption in urban China

论文来源：PNAS

论文链接：https://www.pnas.org/doi/10.1073/pnas.2210853119

中国是公认的最大能源消费国，也是人口最多、老龄化速度最快的国家。由于老年人和年轻人在消费行为上的巨大差异和对环境的不同态度，持续的人口结构变化可能会重塑中国基于家庭的能源消费模式。然而，目前的研究在预测中国人口老龄化对能源消费的影响时，很少考虑到人口结构转型过程中的“代际间的认知差异”。在本文中，研究者评估了中国人口结构转型对能源消费的未来影响，并提出了一个能区分年龄和代际效应的理论框架。具体而言，该研究使用“年龄-时期-对列”模型（age- period- cohort, APC）去趋势分析，根据 1992 年至 2015 年中国城市住户调查数据评估年龄和代际效应。结果表明，不同的年龄和代际对于能源的使用倾向存在巨大差异。老年人和年轻一代往往是能源密集型消费者，这会导致老龄化社会的能源消耗更高。因此，研究表明中国的老龄化将在未来导致能源消耗大幅增加。到 2050 年，老年人口的变化消费份额将占住宅能源消费总量的 17% -26%，接近 1.15 亿吨标准煤。这些研究结果强调了将环境教育政策和人口结构转型结合的必要性，以促进儿童和青年的节能行为，实现低碳、可持续发展。

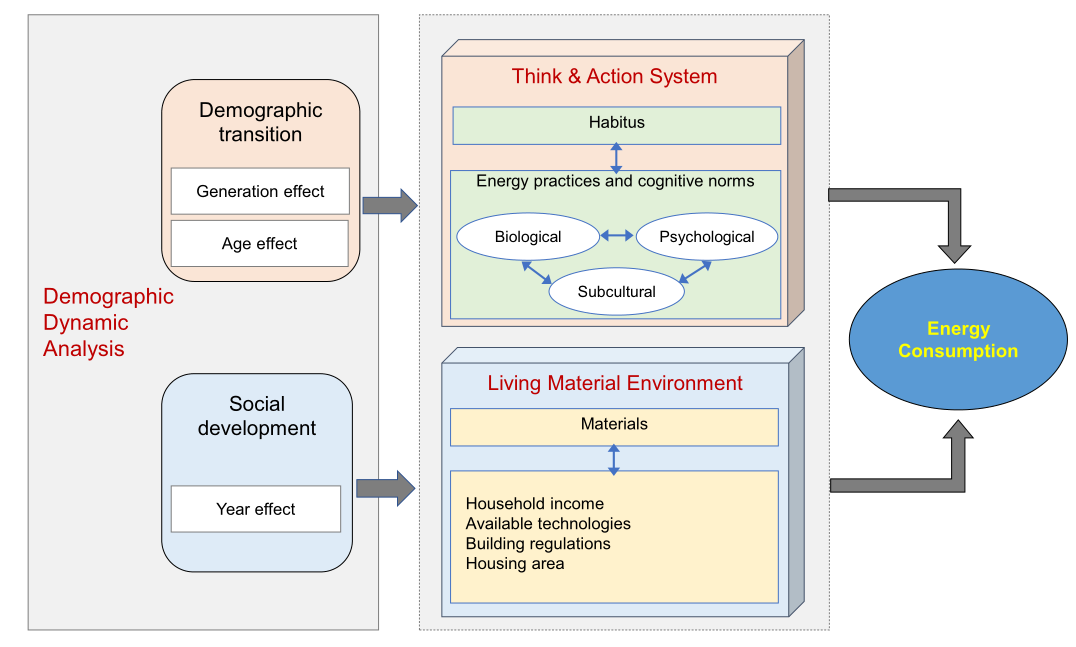
图：人口结构转型对能源消费的影响机制。

7.破碎景观中的多物种共存

论文题目：Multispecies coexistence in fragmented landscapes

论文来源：PNAS

论文链接：https://www.pnas.org/doi/10.1073/pnas.2201503119

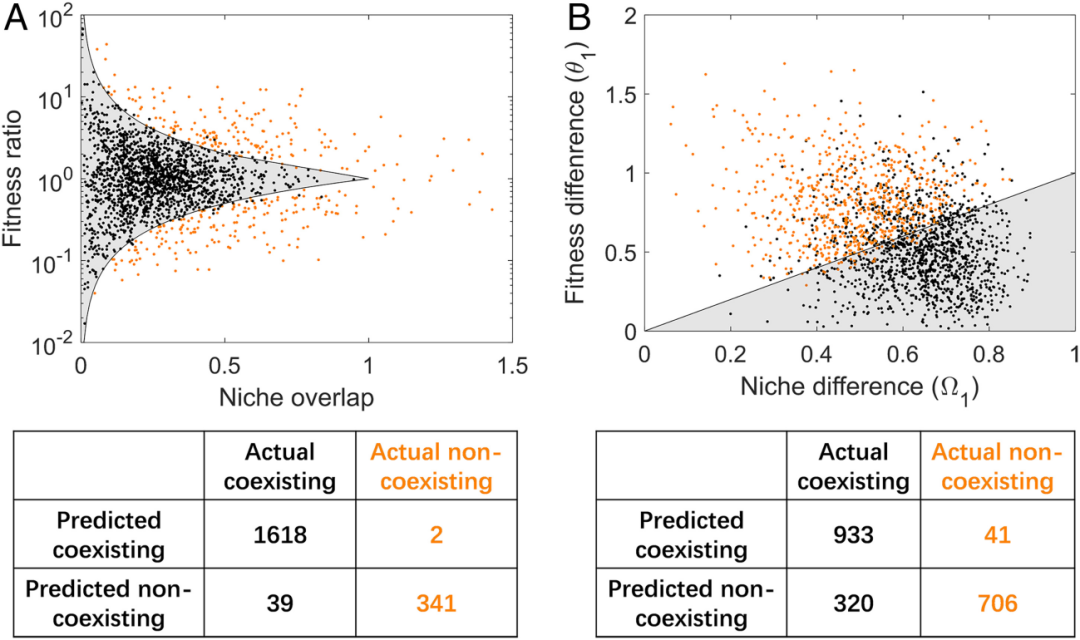
长期以来，空间动力学被认为是生物多样性的一个重要驱动因素。然而，由于缺乏足够的分析工具，我们对现实景观配置下的物种共存的理解一直受到限制。为了填补这一空白，我们建立了一个空间上明确的多个竞争物种的元群落模型，并推导出它们在破碎的异质地貌中共存的分析标准。具体来说，我们提出了元群落的生态位和适应性差异的测量，阐明了空间动力学和栖息地配置如何与局部竞争相互作用，以决定物种的共存。我们用贝叶斯方法对我们的模型进行了参数化，使用了一个 36 年的时间序列数据集，该数据集涵盖了岩石池元群落中的三个水蚤物种，有超过 500 个斑块。

我们的研究结果表明，在灭绝和重新定殖过程中出现了种间变异，包括它们对栖息地大小和环境温度的依赖性。我们发现，这种种间变异通过减少适应性差异和增加生态位差异，有助于水蚤物种的共存。此外，我们的参数化模型可以分离出栖息地破坏和温度变化对物种灭绝的影响。通过整合共存理论和元群落理论，我们的研究提供了平台，以增加我们对物种在破碎的异质景观中的共存以及生物多样性对环境变化的反应的理解。

图：两个（A）和三个（B）竞争物种在破碎的异质景观中的模拟结果。每一点表示 2000 个模拟元群落中的一个，其中所有物种共存（黑色）或至少一个物种灭绝（橙色）。灰色区域表示由我们的标准预测的共存区域。每张图下面的表格显示了预测共存（第一行）或不共存（第二行）以及显示共存（第一列）或排斥（第二列）的模拟元群落的数量（总共 2000 个）。

8.超光速信号在闵可夫斯基时空中的

不可能性并不排除因果循环

论文题目：Impossibility of Superluminal Signaling in Minkowski Spacetime Does Not Rule Out Causal Loops

论文来源：Physical Review Letters

论文链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.129.110401

因果关系是科学的基础，但它以几种不同的形式出现。一种是相对论的因果关系，它与时空结构相联系，禁止在未来之外发出信号。第二个是因果关系的操作性概念，考虑到物理系统之间的信息流和对它们的干预。在论文 [V. Vilasini and R. Colbeck, General framework for cyclic and fine-tuned causal models and their compatibility with space-time, Phys. Rev. A 106, 032204 (2022).] 中，我们提出了一个框架，用于描述一个因果模型何时可以与相对论原则共存，比如没有超光速信号，同时允许循环和非经典的因果影响以及没有信号的因果关系的可能性。

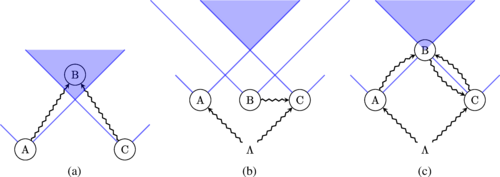
在一个没有超光速因果关系的理论中，超光速信号传递和因果循环在闵可夫斯基时空（Minkowski）都是不可能的。这里我们证明，如果只禁止超光速信号传递，超光速因果关系仍然是可能的，并显示了因果循环在数学上的可能性，这种因果循环可以嵌入闵可夫斯基时空而不导致超光速信号传递。在给定的时空中存在这样的环路，原则上可以用干预措施进行操作验证。这就确定了没有超光速信号的物理原理本身并不足以排除闵可夫斯基时空事件之间的因果循环。有趣的是，排除一个时空中的因果循环所需的条件取决于维度。这种环路在三个空间维度上是否可能，仍然是一个重要的悬而未决的问题。

图：三个因果模型的例子和它们在（1+1）- Minkowski 时空的兼容嵌入。在每个例子中，与模型相关的操作性因果结构用黑色给出，圈出的变量是观察到的节点，而未圈出的则不是，黑色箭头表示因果关系。时空信息用蓝色给出，时间沿纵轴，空间沿横轴。实线代表类光表面，阴影区域对应于所有情况下 A 和 C 的联合未来。

关于Complexity Express

Complex World, Simple Rules.

复杂世界，简单规则。

由于学科交叉融合，大量针对复杂系统的研究成果散落在人工智能、统计物理、网络科学、数据科学、计算社会科学、生命科学、认知科学等等不同领域的期刊会议中，缺乏整合。

 

为了让大家能及时把握复杂系统领域重要的研究进展，我们隆重推出「Complexity Express」服务，汇总复杂系统相关的最新顶刊论文。

 

Complexity Express 是什么？

Complexity Express 每天爬取复杂系统领域最新发表的顶刊论文，每周通过“集智斑图”服务号汇总推送。

 

进入 Complexity Express 页面即可随时查看顶刊论文更新，你也可以通过微信接收研究更新推送和一周汇总。

               

Complexity Express 为谁服务？

• 如果你是复杂系统领域的研究者，可获得重要论文上线通知，每周获取最新顶刊论文汇总。

• 如果你是复杂系统领域的学习者，可了解学界关注的前沿问题，把握专业发展脉络。

• 如果你是传统的生命科学、社会科学等学科中的研究者/学习者，可以从复杂科学和跨学科研究中获得灵感启发。

• 如果你是关注前沿研究发现的知识猎手，可获得复杂系统研究对自然和人类世界的最新洞见。

Complexity Express 栏目也是集智俱乐部公众号的主要选题来源，诚挚邀请你订阅，与我们信息同步。

 

Complexity Express 论文从哪里来？

考虑复杂系统研究往往属于跨学科工作，我们主要抓取综合类和泛物理类/计算机类的顶级期刊，从每周新发表的数百篇论文中精选出与复杂系统相关的论文。

 

Complexity Express 参考影响因子和学者口碑，选择了如下期刊，每日爬取其论文更新：

• Nature

• Science

• PNAS

• Nature Communications

• Science Advances

• Physics Reports

• Physical Review Letters

• Physical Review X

• Nature Physics

• Nature Human Behaviour

• Nature Machine Intelligence

• Review of Modern Physics
• Nature Review Physics
• Nature Computational Science
• National Science Review
• 更多期刊持续增补中，欢迎推荐你认为重要的期刊！

 

如果你在 Complexity Express 中发现了感兴趣的论文，请立刻“点赞”！每周最高赞的论文，集智编辑部将组织专业解读~

 

Complexity Express 追踪哪些领域？

我们力求兼顾热点追踪与领域覆盖，目前筛选的论文主要集中在如下与复杂性关系密切的领域：

• 复杂系统基本理论
• 复杂网络方法及应用
• 图网络与深度学习
• 计算机建模与仿真
• 统计物理与复杂系统
• 量子计算与量子信息
• 生态系统、进化、生物物理等
• 系统生物学与合成生物学
• 计算神经科学与认知神经科学
• 计算社会科学与社会经济复杂系统
• 城市科学与人类行为
• 科学学
• 计算流行病学
• 以及一些领域小众，但有趣的工作

 

由于复杂性研究领域横跨多个学科，研究论文散落在不同的期刊上，很难不重不漏地把握最新工作。针对复杂性领域的论文筛选，我们专门设计了算法。经过数月的训练迭代优化，目前对上述领域爬取准确率达到90%以上。

 

将来我们还会根据你的具体研究领域，推出研究分类与个性化的订阅服务，敬请期待！

 

由于复杂性领域涉及的论文关键词和研究问题纷繁复杂，所以算法难免有不成熟的地方，如果你发现我们有漏掉的重要论文，或者爬到了领域有偏差的论文，欢迎联系我们（小助手微信：swarmaAI），帮助我们持续优化算法。

如果你对科学学、计算术语学等感兴趣并有代码能力，欢迎报名成为集智算法志愿者/实习生（具体请邮件联系算法组负责人huqiao@swarma.org）。

如果你对复杂科学及相关跨学科研究有长期兴趣，并乐于解读分享，欢迎加入集智作者团队（具体请邮件联系编辑部负责人liupeiyuan@swarma.org）。

更多论文

更多复杂性顶刊论文，请到Complexity Express页面查看。订阅即可每周获取更新提醒。

       

点击“阅读原文”，追踪复杂科学顶刊论文