无量纲数和标度律提供了对物理系统性质的深刻见解。对于控制方程不完备的多变量系统,经典的量纲分析和相似理论(similitude theory)无法识别一组唯一的无量纲数。本文介绍了一种机械数据驱动的方法,将量纲不变性原理嵌入到两级机器学习中,从少量且带噪音的测量数据中识别主导的无量纲数和控制律(包括标度律和微分方程)。这种被称为无量纲学习(dimensionless learning)的方法是一种基于物理学的降维学习技术。它可以将高维参数空间削减为少量物理上可解释的无量纲参数,大大简化了复杂过程设计和系统优化。
关键词:无量纲数,标度律,机器学习,瑞利-贝纳德对流
论文题目:Data-driven discovery of dimensionless numbers and governing laws from scarce measurements
论文地址:https://www.nature.com/articles/s41467-022-35084-w
所有的物理定律都可以用无量纲关系表示为更紧凑的形式。无量纲数是一些物理量的幂律单项式(power-law monomials)。无量纲数没有物理尺度(例如质量、长度或能量),从而具有尺度不变性,即当系统的长度、时间尺度或能量尺度发生变化时,无量纲数是不变的。在物理、物理化学、流体力学、固体力学、热力学、电磁学、地球物理学、生态学以及工程学等领域,已经发现了超过1200个无量纲数。
使用无量纲数描述物理过程或系统有几个显著的优势,包括减少变量的数量,支持跨尺度实验,以及增加物理可解释性。首先,无量纲数可以减少描述物理过程的变量,从而大大简化问题,减少了理解和设计物理系统所需的实验数量。例如,雷诺数(Reynolds number)是流体力学中一个著名的无量纲数,以 Osborne Reynolds 的名字命名。他在1883年研究了流体在管道中的流动,基于流体密度、平均流体速度、管道直径和动态粘度四个物理量定义了雷诺数,它能比四个物理量更好地判断管道中流体的特性(层流或湍流)。其次,无量纲数的尺度不变性在相似理论中有至关重要的作用。航空航天、核工程和海洋工程昂贵且危险的实验可以通过小尺度实验来理解和预测,原因就在于所有尺度的实验,无量纲数都是相同的,其几何、动力学和运动学也都具有完美的相似性。第三,无量纲数是几个物理量的比值,因此在物理上具有可解释性,可以洞见复杂系统的行为。
尽管无量纲数具有重要的科学意义和广泛的应用,从实验中发现新的无量纲数及其关系(即标度律)仍然具有挑战性,特别是对于缺乏完整控制方程的复杂物理系统而言。对此,惯用的解决方法是量纲分析,它基于π定理(Pi theorem)检查物理系统的单位,并产生一组满足量纲不变性原理的无量纲数。然而,量纲分析有几个众所周知的局限性。其一,根据π定理得出的无量纲数不是唯一的。其二,量纲分析本身不能揭示无量纲数之间的数学关系。标度律的建立很大程度上依赖领域专家的经验以及长期的试错。
针对这些问题,近日发表在 Nature Communications 的一篇文章提出了一种机械的数据驱动方法,称为无量纲学习(dimensionless learning)。该方法通过两个流程从数据中发现科学知识。第一个流程将量纲不变性原理(即物理定律独立于测量数据的基本单位)嵌入到两级机器学习中,从复杂物理系统带噪声的实验数据中发现主导的无量纲数和标度律,所研究的对象包括瑞利-贝纳德对流(Rayleigh–Bénard convection),激光熔融金属过程的蒸汽压缩动力学,以及3D打印中的孔隙形成。第二个流程将无量纲学习与稀疏促进技术(sparsity-promoting technique)结合起来,从数据中识别无量纲齐次微分方程和无量纲数。
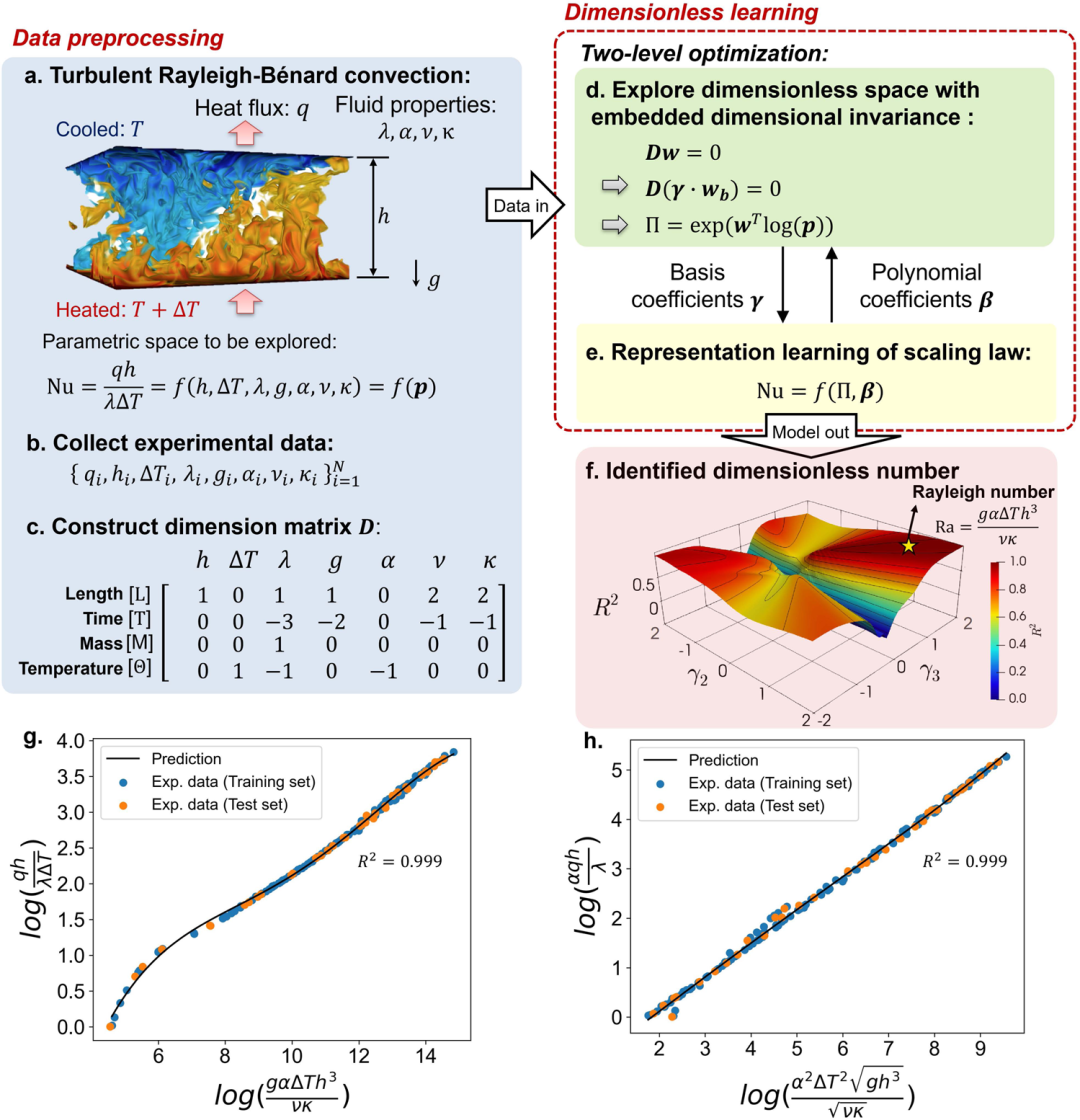
本文通过瑞利-贝纳德对流(Rayleigh–Bénard convection)这一经典流体力学问题来演示无量纲学习的第一个流程。该流程的目标是从实验数据中重新发现瑞利数(Rayleigh number,Ra)这一无量纲数。瑞利数以瑞利勋爵命名,他在1916年研究了一种非等温浮力驱动的流体,现在被称为瑞利-贝纳德对流,是研究自下而上加热容器中水平平面流体热流动的典型系统。由于浮力、流体粘度和重力的影响,内部流体可以发展出复杂的湍流动力学(图1a)。
图1.所提出的无量纲学习在瑞利-贝纳德对流中的演示。(a)瑞利-贝纳德对流示意及其相关物理量。(b)实验测量的物理量。(c)构造输入变量的量纲矩阵 D。(d)二级优化的第一级,训练关于基向量的系数 γ。(e)二级优化的第二级,优化表征学习中的未知系数β。(f)以R2度量的无量纲空间,R2 最大的位置标有黄色星号,对应瑞利数。(g)识别出 Nu 和 Ra 间的一维标度律。(h)发现两个无量纲数间的线性标度律。
无量纲学习的第二个工作流程,是从时变数据中识别量纲齐次微分方程和无量纲数。该流程将稀疏促进方法与无量纲学习结合。在上一流程的瑞利-贝纳德问题中,量纲不变性被嵌入机器学习。与此类似,这一流程将另一个基本的物理不变性——对称不变性——用于增强稀疏促进方法SINDy(sparse identification of nonlinear dynamics,一种用于从数据中发现系统动力学模型的算法),将其称为对称不变 SINDy。
该流程从卡门涡街问题的模拟快照中识别基本的控制方程和无量纲数,图2为其示意图。这一流体力学问题涉及三个直径为 l 的圆柱体(图2-a)。通过改变流体密度 ρ、动态粘度 μ、入口速度 v 和上下游间的压差p0,可以模拟出不同的流体流动模式。
图2.无量纲学习与对称不变 SINDy 的结合,用于识别包含雷诺数的 Navier-Stokes 方程。(a) 原始数据由参数模拟产生。为实现对称不变性,将原始数据沿 y=x 翻转,得到另一组转换后的数据。(b) 将原始数据和转换后数据合并用于对称不变 SINDy,从而隐含地将对称不变性融入到 SINDy 中,以确保对称不变项具有相同的系数。(c)优化对称不变 SINDy,得到了每种模拟情况下识别出的临时控制方程。有些系数接近于常数,有些系数根据模拟情况而变化,其它候选项的系数则都为零。(d)应用无量纲学习方法识别变化系数的显式表达。要探索的参数空间包括五个参数,引入量纲不变性后需要优化基系数 γ 和拟合系数 β。(e)将已发现的回归系数(1/Re)代入临时控制方程,得到了稳定的量纲齐次控制方程,与涡量形式的 Navier-Stokes 方程一致。
无量纲学习是一项强有力的技术,可从多个层面的数据中识别科学知识:物理特征层面的无量纲量,代数方程层面的标度律以及微分方程层面的控制方程。与之对比,纯数据驱动方法很容易在小数据集或噪声数据集上过度拟合,无量纲学习则将量纲不变性和对称不变性的基本物理知识作为约束纳入数据驱动模型,以便在有限且带噪声的数据上表现良好。嵌入的物理不变性缩小了学习空间,消除了变量之间的强相关性。
该方法本质而言是一种基于物理学的降维方法,它将物理特征表示为无量纲数,并将数据点转换为不受单位和尺度影响的低维模式,从而显著改善了表征学习的可解释性,能够对系统定性和定量分析。
无量纲学习不仅可广泛用于物理、化学和生物系统,还尤其适用于工程问题。先进材料加工和制造,输送药物流体的精确控制,太阳能系统设计等工程问题都涉及大量具有不同尺度或单位的可调参数,而无量纲学习可以将问题简化为仅涉及少量具有明确意义的无量纲参数,以指导工程应用。
跨尺度、跨层次的涌现是复杂系统研究的关键问题,生命起源和意识起源这两座仰之弥高的大山是其代表。而因果涌现理论、机器学习重整化技术、自指动力学等近年来新兴的理论与工具,有望破解复杂系统的涌现规律。同时,新兴的因果表示学习、量子因果等领域也将为因果涌现研究注入新鲜血液。
集智俱乐部特别组织「因果涌现」系列读书会,深入研读相关文献,激发科研灵感。目前已经进行了两季,聚集了500+成员,积累了大量论文解读资料。欢迎感兴趣的朋友报名,加入因果涌现社区,并解锁对应录播权限。
读书会详情与报名方式请参考:
因果涌现读书会启动:连接因果、涌现与自指——跨尺度动力学与因果规律的探索
因果、涌现与机器学习:因果涌现读书会第二季启动