PRL：测量活性物质系统中的局部熵产生

导语

时间反转对称性破缺和熵产生是非平衡态系统的普遍特征，在活系统和生命系统的物理学中占有重要地位。但这类复杂系统具有多个自由度，其状态空间的高维度使得系统的熵产生率难以测量。近日发表于 Physical Review Letters 的新研究介绍了一种测量活性物质系统中局部熵产生率的方法，并在理论、模拟和活性布朗粒子与大肠杆菌的实验中做了验证。该方法可用于对熵产生率的量化及可视化。

关键词：非平衡系统，活性物质，熵产生，时间对称性破缺，信息论

Matteo Paoluzzi | 作者

郭瑞东 | 译者

梁金 | 审校

邓一雪 | 编辑

论文标题：

Model-Free Measurement of Local Entropy Production and Extractable Work in Active Matter

论文地址：

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.129.220601

一个影片中，如果处于平衡态的流体中分子相互碰撞，那么向前和向后播放时看起来是一样的。这一过程的“熵产生率”（entropy production rate）——用来量化这种对称性的参数ーー为零，而大多数其他过程都为非零，这意味着被观测的系统处于非平衡态。

研究人员知道如何计算简单模型系统的熵产生率。但是在实验中测量这个参数是一个开放问题。现在，以色列理工学院的 Sungham Ro、纽约大学的 Buming Guo 和他的同事们开发了一种测量局部熵产生率的方法[1]。他们使用模拟和对细菌的观察来演示这项技术（图1）。这种方法包括比较正向和时间反转的粒子轨迹，可以让研究人员揭示局部熵产生率对复杂生命系统（从细胞到组织）的全局动力学的影响。

图1. 研究人员开发了一种方法，可以直接测量活性物质系统的局部熵产生率。图中，活性布朗粒子通过一系列漏斗被驱动到环结构的中心。熵产生率高的区域是黄色，熵产生为零的区域是黑色。

1. 活性物质系统

活性物质系统是由能量消耗主体组成、表现出复杂集体行为的的系统[2-4]。典型例子是鸟群和鱼群，它们之前存在大量的相互作用，可以群体俯冲或旋转。这些系统由于持续的能量消耗[5]，在单主体（single-agent）层次上打破了时间反转对称性，因此活性物质系统在局部尺度上熵产生率非零[6]。

科学家还知道，活性物质系统在全局尺度上打破了时间反转对称性，人们观察到这些主体集体组织成一种模式，比如鱼群或鸟群，其长度尺度比主体本身大得多。然而，我们不知道，全局和局部时间反转对称性破缺之间存在何种联系。仅仅知道全局系统的局部熵产生率非零，并不能告诉我们太多关于系统行为的信息。例如，它告诉我们系统作为一个整体离平衡态有多远，但不告诉我们系统处在远离平衡态的哪个位置。此外，我们对系统在中等尺度上的热力学性质变化仍然一无所知。了解这一点，可以让科学家将活性物质系统的局部动力学与其全局模式形成联系起来，使他们能够利用其中一个来预测另一个。

为了获得这些信息，科学家曾建议使用基于场论的方法（field-theoretical approaches）计算局部熵产生率，但这个想法只在几个特定的模型中进行了测试[7-9]。采用场论捕捉熵产生率，需要收集向前过程中的“平稳”（stationary）轨迹（类似电影的帧），然后将这些帧与时间反转的影像中的帧进行比较。这种比较应该可以让我们量化系统中非平衡行为最明显的区域。然而，准确地量化平稳轨迹和时间反转轨迹之间的差异是具有挑战性的[10]。Ro, Guo 和同事们的工作接受了这一挑战。

2. 测量局部熵产生

在这项研究中，研究小组考虑了一种通用的活性物质系统，该系统由在空间中随机移动的自推进粒子组成，进行“持续性”随机游走——粒子大致沿直线移动的一种特定类型的随机游走。

研究者将系统分散到网格上，将网格的每个点与一个整数联系起来，取一组有限数值中的一个值，取决于该位置是否有粒子（图2）。分配给每个点的值随时间变化，组成一个特定的时间序列。对于时间反转的影片，团队获取这些序列中的每一个，并反向播放：最后一个值变成第一个值。

模型获得两个影片中的序列，并使用一个称为交叉解析长度（cross-parsing length）的参数进行比较，交叉解析长度在信息理论中用于量化两个序列中共享模式的数量[11]。在正向和反向影片中共享的模式越多，它们在时间上就越对称，熵产生率就越低。因此，交叉解析长度与局部熵产生率有关。

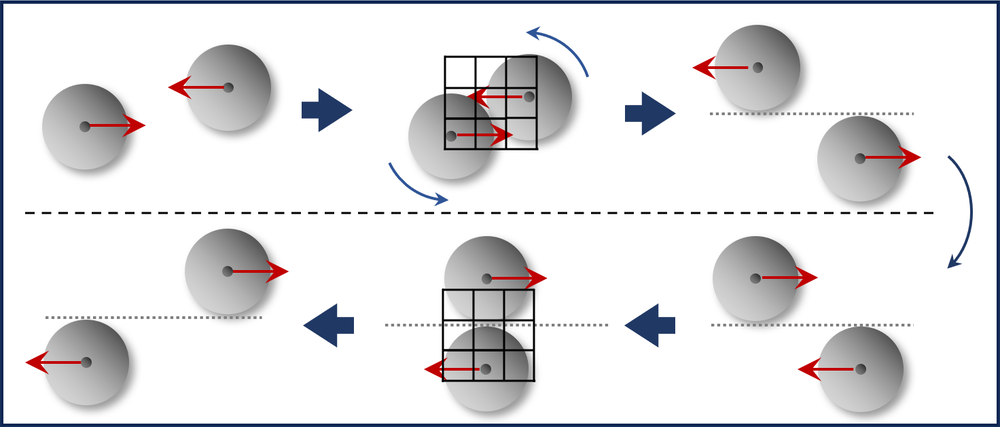
图2. 图片展示了活性粒子之间的碰撞如何打破时间反转对称性。上面一行记录碰撞前（左）、碰撞中（中）和碰撞后（右）两个活性粒子的位置。下面一行显示了碰撞过程的时间反转。这两个场景中的最终状态是不同的，导致这些正向和反向影片之间缺乏共享模式，从而系统的熵产生率为非零。

为了对他们的方法进行基准测试，Ro、Guo 和同事们将其应用于活性布朗粒子的数值模拟上，这些布朗粒子经历所谓的运动诱导相分离——粒子在密集的团簇中移动较慢，形成一个具有密集和稀疏区域的系统；还在大肠杆菌通过漏斗导入特定区域的实验中进行了验证。对于布朗粒子的数值模拟，他们发现熵产生率在密集和稀疏区域之间的边界处最高，在中心处最低。在大肠杆菌实验中，他们发现漏斗周围的熵产生率最高。

3. 探索非平衡态

Ro、Guo 和同事们引入的计算方法将使研究人员能够开始更详细地探索天然和人造活性物质系统的非平衡特性。原则上，这可能引导人们进一步研究，非平衡特征如何在生命系统中传播，以及这些特征如何与系统形成的模式相联系。例如，它可以让科学家为细胞创建非平衡态的“地图集”，并更好地理解非平衡态如何对应到生物体的集体行为。

原文链接：

https://physics.aps.org/articles/v15/179

参考文献

1. S. Ro et al., “Model-free measurement of local entropy production and extractable work in active matter,” Phys. Rev. Lett. 129, 220601 (2022).

2. M. C. Marchetti et al., “Hydrodynamics of soft active matter,” Rev. Mod. Phys. 85, 1143 (2013).

3. C. Bechinger et al., “Active particles in complex and crowded environments,” Rev. Mod. Phys. 88, 045006 (2016).

4. M. J. Bowick et al., “Symmetry, thermodynamics, and topology in active matter,” Phys. Rev. X 12, 010501 (2022).

5. E. Fodor et al., “Irreversibility and biased ensembles in active matter: Insights from stochastic thermodynamics,” Annu. Rev. Condens. Matter Phys. 13, 215 (2022).

6. E. Fodor et al., “How far from equilibrium is active matter?” Phys. Rev. Lett. 117, 038103 (2016).

7. C. Nardini et al., “Entropy production in field theories without time-reversal symmetry: Quantifying the non-equilibrium character of active matter,” Phys. Rev. X 7, 021007 (2017).

8. F. Caballero and M. E. Cates, “Stealth entropy production in active field theories near Ising critical points,” Phys. Rev. Lett. 124, 240604 (2020).

9. M. Paoluzzi, “Scaling of the entropy production rate in a 𝜙4 model of active matter,” Phys. Rev. E 105, 044139 (2022).

10. E. Roldán and J. M. R. Parrondo, “Entropy production and Kullback-Leibler divergence between stationary trajectories of discrete systems,” Phys. Rev. E 85, 031129 (2012).

11. J. Ziv and N. Merhav, “A measure of relative entropy between individual sequences with application to universal classification,” IEEE Trans. Inform. Theory 39, 1270 (1993).

集智俱乐部因果涌现社区

跨尺度、跨层次的涌现是复杂系统研究的关键问题，生命起源和意识起源这两座仰之弥高的大山是其代表。而因果涌现理论、机器学习重整化技术、自指动力学等近年来新兴的理论与工具，有望破解复杂系统的涌现规律。同时，新兴的因果表示学习、量子因果等领域也将为因果涌现研究注入新鲜血液。

集智俱乐部特别组织「因果涌现」系列读书会，深入研读相关文献，激发科研灵感。目前已经进行了两季，聚集了500+成员，积累了大量论文解读资料。欢迎感兴趣的朋友报名，加入因果涌现社区，并解锁对应录播权限。

读书会详情与报名方式请参考：

因果涌现读书会启动：连接因果、涌现与自指——跨尺度动力学与因果规律的探索

因果、涌现与机器学习：因果涌现读书会第二季启动

推荐阅读