网络科学在不同研究领域的应用数量一直在迅速增加。令人惊讶的是,理论的发展和特定领域的应用往往是相互独立的,这就有可能造成理论进步与实践应用之间产生脱节。最近,发表于 Nature Communications 讨论了这一问题,并提出了保证更成功的应用和可重复的结果的相关建议。这篇文章强调以统计学为基础的方法论来解决网络科学中的挑战。这种方法允许人们用生成模型来解释观测数据,自然地处理内在的不确定性,并加强理论和应用之间的联系。
Leto Peel, Tiago P. Peixoto & Manlio De Domenico | 作者
刘志航 | 译者
刘培源 | 审校
邓一雪 | 编辑
论文题目:
Statistical inference links data and theory in network science
https://www.nature.com/articles/s41467-022-34267-9
1. 绪论
2. 连接网络科学中的数据和理论
3. 模糊的数据质量
4. 表示方法的选择
5. 方法的适用性
6. 展望
网络科学是对复杂系统的研究,该系统由基本单元(以节点表示)和它们的相互作用或关系(以链接表示)组成[1,2]。这种数学抽象提供了将相互作用的系统作为一个整体来研究的机会,并使我们能够发现重要的见解。如果我们将系统作为一个简单的单元集合来研究,我们可能会错过这些见解,例如将系统简化为各部分的总或任何其他天真的聚合。此外,网络科学指向一个统一的范式,可以用来描述属于不同科学领域的系统,但仍然可以被映射为一个由相互作用的元素组成的网络。事实上,这种整体处理方法已被用于研究各种复杂系统,包括生物(从细胞生物学[3-5]到神经回路[6-8]和生态食物网[9-11])、技术(从耦合的基础设施[12,13]到通讯系统[14,15])和社会系统(从社会技术关系[16-19]到动物互动[20,21]),加强了我们对社会[22,23]、生命[24-26]和疾病[27-29]以及它们的组合[30-35]中的涌现现象的理解。
尽管如此多的学科接受了这种整体论思想,但我们也许会惊讶地发现,网络科学理论的发展与在特定领域的应用往往是孤立的。这种脱节的后果是:(1)一般的网络科学方法的开发通常不考虑基础数据的出处;(2)网络科学方法被误用或断章取义。出现这些问题的原因是:一方面,方法的开发和测试往往很少考虑固有的不确定性,以及现成经验数据的不完整性,甚至没有深入了解其来源和测量程序。另一方面,涉及到数据收集和后续分析的原始经验性工作,往往采用现成的方法,这些方法可能与数据或研究领域不相容。也许这种理论和应用的脱节可以被认为是一种简单而方便的专业化分工,当个别研究者在某一领域内进行专业研究时,这种分工自然会发生。有人可能会说,这种专业化是合理的,为解决特定的挑战提供了更有效的途径,甚至是科学研究的竞争环境中蓬勃发展的必要条件。
在这里,我们将讨论在网络科学这样一个多样化和跨学科的领域中,这种脱节所带来的一些风险以及各种各样的潜在问题。从忽视目标研究问题的理论泛滥到应用方法忽视基本假设和限制。使用不恰当的方法或盲目应用方法来代替清晰的理解,有可能在网络科学有机会完全绽放之前就凋谢,并会破坏那些从理论到应用问题的科学家们二十多年来为对话和争鸣所做的努力。
我们想强调的核心问题是,方法和实践之间的脱节会抹去数据(即实际测量的东西)和抽象(即基础网络表示)之间的关键区别。很多时候,研究人员会选择从手头的测量结果到网络表征画一条最短的线,而忽略了一个事实,即网络元素之间的实际交互通常只在观察中间接表现出来。这种情况的发生有多种原因,包括测量的不确定性、数据的不可控性或不恰当的选择表示。
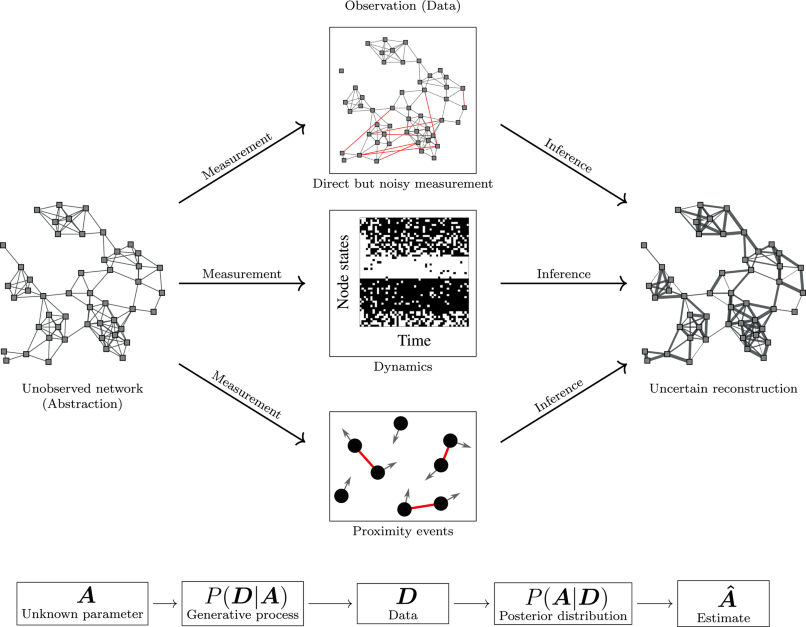
在此,我们认为最合适的解决方案是将网络分析作为一个统计推断问题,因为实际的网络抽象其实隐藏在视图之外,需要在给定间接数据的情况下进行重构。我们在方框1中说明了这一点,在那里我们展示了一些间接测量的例子,包括完整和错误的网络、时间序列动力学和邻近事件,它们只间接地指向需要重构的底层网络结构。
在这项工作中,我们将关注三个密切相关的因素,由于上述网络科学理论与实践之间的差距,这些因素往往被忽视:(1)模糊数据的质量。(2)表示方法的选择。(3)方法的适用性。我们认为,为了缩小这一差距,有必要采用以模型为中心的方法来进行数据驱动的网络分析,这需要一个适当的抽象水平来描述研究对象(通常在数据中无法直接观察到),以及一个推断步骤,使我们能够从手头的(可能是间接的)数据中提取这一抽象概念。提供这种联系的方法应该从第一性原理中推导出来,并且应该为特定的应用领域量身定做。
我们将展示由于模糊了数据和抽象之间的区别而导致的典型陷阱,最近为解决这些问题所做的工作,以及现有的挑战和未探索的开放问题。我们主要关注网络的结构分析,因为确定网络结构通常是任何网络分析的第一步。然而,我们提出的观点同样适用于对网络的经验测量分析,即在网络上发生的动力学过程。
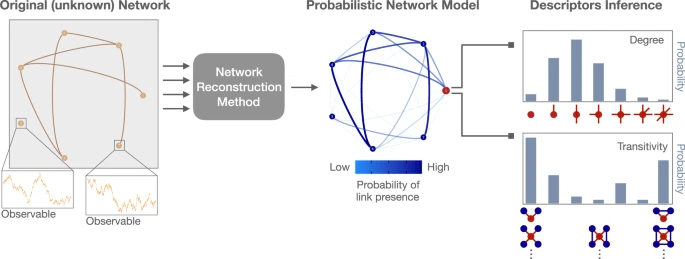
方框1:网络科学中数据与理论的联系。一般来说,不应该把作为结果给出某种观测数据 D 的相互作用网络 A 与数据本身混为一谈。相反,我们需要认识到,数据 D 是测量过程 P(D∣A) 的结果,它以未见的网络为条件,但在某种程度上不可避免地与它脱钩。为了估计底层网络,我们需要执行一个推理步骤 P(A∣D),这需要包括我们对网络和数据如何产生的建模假设。由此产生的估计值会有一个不确定性,反映了实验设计、测量的准确性和特定重构问题的整体可行性。
当考虑网络数据时,测量的不确定性几乎被普遍忽视,实证研究经常是假设真实系统的网络表示是完全准确的情况下进行的,这种做法在既定的实证领域早已被抛弃,是站不住脚的。由于实际原因,观测数据通常是不完整的,研究人员会面临数据集是否具有代表性或有偏的,以及在何种程度上具有代表性的问题。举个简单的例子,调查数据中的受访者可能会以不同的方式解释问题,从而有可能产生不一致的情况[36],对植物和授粉者物种之间相互作用的观察可能会因为偶然性[37],或因为一些物种比其他物种更难发现而错过授粉接触。此外,即使数据收集过程足够准确,可以忽略这些不确定因素,但总是有可能包含转录或复制错误。这对一个实验者来说可能是微不足道的,但网络科学背景的异质性意味着不同程度上是潜在的问题,而且常常被完全忽略。
一个典型的例子是 Zachary 的空手道俱乐部网络,它代表了一个空手道俱乐部的成员之间的社交互动[38]。这个网络是发展网络科学方法的最简单和最广泛使用的社会网络之一,最常被用作标准测试网络,而不是作为研究对象。值得一提的是,论文中一个明显的转录错误,它妨碍了对数据进行完全明确的计算:记录的邻接矩阵包含一个可证明的错误,因为条目(23,34)为零,而条目(34,23)为非零,尽管该网络是无向的。这种模糊性在原论文中提出的矩阵的加权和非加权版本中都会出现。此外,即使人与人之间的互动被 Zachary 完整无误地手工记录下来,研究界也无法获得基本的原始数据(直接观察、调查、学校记录)以及相关的不确定性。这种基本测量信息的缺乏,严重限制了最终能从这些数据中了解到的情况。
每当收集关于真实世界的数据时,测量错误和遗漏的可能性应该被认为是通则,而不是例外。通常情况下,那些在特定应用领域工作的研究人员很清楚这些问题,以及这些模糊性在其特定领域的影响。例如,研究社交媒体上人类行为的计算社会科学家会意识到,他们从平台 API 收到的数据是一个完整数据集中可能有偏的子集[39],特定平台的用户集不一定能代表一般人群[40]。然而,在经过预处理并公开提供的数据中,这种特定领域的知识很少被记录,网络科学的计算工具就是在这些数据的基础上发展起来的。缺乏描述原始数据质量的元数据意味着,许多网络科学的工具是建立在隐含的假设之上的,即网络的构建是完美的,数据中没有错误或遗漏,这一点很少能够被证明。正因为如此,所有的数据都含有一定量的不确定性,这一颇具争议的事实几乎从未被纳入网络分析及其结论中,对这一事实的任何认识(最多)都只是作为一种事后的告诫或免责声明。
这里的核心问题不是准确性本身,而是缺乏误差评估。网络数据在本质上并不比任何其他类型的经验数据更少或更准确。然而,网络数据中的误差很容易在网络分析中被放大,而且由于其依赖网络结构的高度非线性性质,其方式很难预测,这使得我们很难估计最终结论的不确定性。图1说明了这个问题,我们模拟了两个经验网络的噪声,一个是高中生之间的友谊[41],另一个是政治博客之间的超链接连接[42]。这些网络本身是经过测量的,因此包含它们自己的未知误差。然而,为了本模拟的目的,我们假设它们是完整的,没有任何错误。基于这个虚构的“真实”网络,我们模拟一条边没有被记录(“假阴性”),其概率为 p,而一条非边被记录为边(“假阳性”)的概率为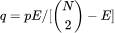 其中N和E是原始网络中的节点和边的数量。以这种方式选择概率 q,使观察到的边的预期数量与原始网络中的相同。人们可能会天真地认为,这种均匀的测量误差的影响仅仅是为原始网络的网络描述符(descriptors)的值引入波动。相反,我们观察到系统性的偏差,将这些值转移到特定的方向,使它们不再与原始网络的值相似,重要的是,它们可以隐藏现有的结构或放大现有的结构。
其中N和E是原始网络中的节点和边的数量。以这种方式选择概率 q,使观察到的边的预期数量与原始网络中的相同。人们可能会天真地认为,这种均匀的测量误差的影响仅仅是为原始网络的网络描述符(descriptors)的值引入波动。相反,我们观察到系统性的偏差,将这些值转移到特定的方向,使它们不再与原始网络的值相似,重要的是,它们可以隐藏现有的结构或放大现有的结构。
图1:从噪声网络中测得的网络描述符(descriptors)及其重构。我们研究了两个经验网络:(a)高中生之间的友谊和(b)政治博客之间的超链接,用模拟的缺失边概率 p 和假的边概率 来测量。我们考虑的是以这种有噪声的方式测量出来的网络(“未重构”),以及用参考文献中的贝叶斯方法得到的重构的网络[53]。在进行了 M 个独立的噪声测量后得到的重构网络。我们显示了在每种情况下获得的相应随机行走过渡矩阵的平均局部聚类系数和谱隙的值。误差条对应于后验分布的标准偏差。横线表示原始网络的真实值。
来测量。我们考虑的是以这种有噪声的方式测量出来的网络(“未重构”),以及用参考文献中的贝叶斯方法得到的重构的网络[53]。在进行了 M 个独立的噪声测量后得到的重构网络。我们显示了在每种情况下获得的相应随机行走过渡矩阵的平均局部聚类系数和谱隙的值。误差条对应于后验分布的标准偏差。横线表示原始网络的真实值。
这里需要指出的是,网络科学的早期工作承认网络数据容易出错[43],并为从观察到的网络中推断出缺失链接的任务奠定了基础,这就是后来的链路预测[44]。Goldberg 和 Roth [43]开发了启发式方法来利用新发现的网络的“小世界”特性[45],其他人则使用节点属性来预测缺失的链路[46,47]。从那时起,出现了许多关于链接预测主题的文献[44,48-50],包括研究时序演化网络未来链接的预测[51]。然而,这些工作似乎是在他们自己的“链路预测”研究领域中发展起来的,与网络分析的其他部分几乎没有互动(明显的例外是 Clauset 等人[49]和 Guimerá 等人[48]的工作,他们将链路预测作为一个统计推理问题,基于生成网络模型)。将一个问题分解成独立的子任务可以为我们组织科学发展提供很大的好处,但是这种分离带来的风险是,这些子任务本身就成为一个世界,而它们是一个更大的难题,这一事实很容易被遗忘。在链路预测的具体案例中,研究人员倾向于关注核心理论问题,但往往忽略了基本的实际问题,例如,最强调的是根据最有可能出现的边进行排序,但没有强调应该预测多少条边或错误分类成本的不对称性的影响。将链路预测作为一个排序问题,可以使不同的方法很容易地相互比较,但它本身并没有提供一个完整的方法,可供从业者随时使用。正因为如此,关于链路预测的大量文献并没有产生大量的实际链路预测。
幸运的是,最近,不确定的网络数据的想法已经恢复,并开始回到主流,一些研究人员提出了一个研究议程,致力于在理论上和实践中纳入网络测量中存在的误差和影响。这个方向的第一步是接受数据和抽象之间的基本区别,并接受这样一个事实:无论我们做什么测量,都不一定是我们想要研究的“网络”,而是至少包括一定量的失真。因此,研究一个网络应该以网络重构为框架,我们已经在方框1中介绍了这一点。这个想法通过制定生成模型来实现,生成模型结合了噪声测量(表示为在底层网络 A 下观察数据 D 的概率 P(D∣A) )和潜在的网络结构(编码为先验概率 P(A) ),并通过贝叶斯后验分布,使用这些信息来确定哪些网络更有可能位于某个给定的观察背后。
这种方法是可以任意扩展的,因为我们可以根据需要替换我们的测量模型和先验网络,纳入适当的领域知识,以更好地适应任何特定的应用。
在社会网络的背景下,Butts[36]已经实现了上述方法,以考虑到网络数据的报告错误。Newman[52]也用上述方法展示了如何用多个独立的网络测量值来重构一个网络,这个网络比我们用单个测量值得到的更准确。在 Guimera 等人[48]、Clause t等人[49]和 Airoldi 等人[50]的开创性工作的基础上,Peixoto[53]扩展了这一框架,引入了结构化的网络先验,可以发现潜在的模块化网络结构,并利用这些信息来确定什么更有可能是基础网络,即使是在进行单一网络测量,且误差未知的情况下。Young 等人[54]建立了一个一般的设置,在进行多次测量的情况下,从业人员可以指定一个任意的测量模型。
图1还显示了用参考文献[53]的方法重构网络得到的结果。它更接近于真实值(即使是单次测量,M=1),并且随着独立测量次数的增加而渐进地接近它们。这类结果说明了两个要点:i)更合理的方法是纳入而不是忽视测量误差的可能性,即使在数据的不确定性信息不可用的情况下,也能改善分析;ii)只有进行适当的误差量化(如图1中的多次测量M>1),并在分析中考虑到这些误差,最终才能得到准确的结果。尽管已经有了实现第一种方法的方法,但这些方法仍然可以进一步发展,纳入更现实和多样化的网络模型,并使其在计算上更有效率。然而,这些方法将不可避免地遇到重构的基本限制,只有在数据采集阶段纳入适当的误差量化,这些限制才能被解除。这意味着,只有当网络科学的经验实践不再遗漏这些关键信息时,准确的网络分析才有可能。
尽管离普遍的实践还很远,但我们看到网络科学界至少已经考虑到了数据的不确定性问题,而且对网络重构的重视程度也越来越高,这是很有希望的。然而,需要注意的是,不仅是链接,而且节点(以及它们的属性,或元数据)也可能包含错误,这些错误经常出现在节点身份方面。例如,考虑一个合作网络,其中的节点是作者,如果他们曾一起工作过,就会有联系。这些网络可以从文献计量学数据中构建,但定义一个节点需要在多个出版记录中匹配单个作者。错误很容易出现,因为不同的作者可能有相同的名字,可能导致多个节点被折叠成一个节点,而且一个作者可能有不同的合作者和机构,或者一个名字有多种拼法,可能将一个节点表现为多个节点。这些问题因记录节点属性的错误或差异而进一步加剧,例如,作者的隶属关系往往在不同的期刊上采用不同的格式。
这种节点的不确定性在网络科学文献中还没有真正得到足够的重视。然而,解决这些不确定性之前已经在不同数据源的实体匹配方面进行了探索[55,56]。这个问题通常被称为实体解析,但也有其他名称,如记录链接、重复数据删除、对象识别和身份不确定性等等。虽然这个领域的很多工作没有应用于我们通常表示为网络的数据,但是后来的工作利用了网络结构,以改善匹配[57-59]。
选择相关的变量是任何科学学科中最困难的任务之一,而在网络科学中可能更成问题,因为它涉及的是允许多种表述的复杂系统。
在进行网络分析时,仔细思考什么是节点,什么是边,应该是常见的做法。Butts[60]已经明确提出了这个问题,他警告说定义什么是节点和边是一个对网络分析有关键影响的核心选择。Butts 认为,由于网络的表示总是对基础系统的一种近似,它的构建是一种理论行为,不可能没有假设,而这些假设又需要被明确和审查。
正如我们已经提到的,将网络的特定数学描述与实际的基本调查对象相混淆并不困难。事实上,通常的做法是从手头的数据到网络表征的最短路径,通常被称为“网络”,即使在许多情况下,这可能是忽略了数据和抽象之间的关键区别,对于这些区别,在进入分析阶段之前,至少应该检查一下有许多替代方案。事实上,上面讨论的测量误差的遗漏可以被看作是这种短视的一个特殊症状,但潜在的问题往往远远超出这个范围。作为一个简单的例子,我们可以采取任何网络,并通过用节点取代边来将其转化为相应的线图,大大改变网络的属性[61,62]。从纯数学的角度来看,这两种表示方法都不能被视为“网络”,因为这种转换是可逆的。虽然在大多数情况下,情况远没有这么模棱两可,然而,考虑这样一种可能性是不太常见的,即在某些数据中观察到的成对关系应该更好地理解为某种隐藏关系的间接表现,它可能完全涉及不同的单位,甚至根本不涉及。
再次,我们可以用 Zachary 的空手道俱乐部作为一个简单的例子。在最初的论文中,报告的网络是基于多种观察到的社会互动的一些未知函数,这些函数实际上隐藏了所选择的基本表征。Zachary 网络中的每个链接到底告诉我们空手道俱乐部成员之间的社会互动是什么?由于不知道 Zachary 精确地测量了什么,以及如何测量,因此无法从报告中提取任何真正的科学理解。
一旦我们要求我们的网络抽象是生成过程的一部分,我们就能解决这个问题的很大一部分,这个数学模型至少在原则上能够重现我们观察到的任何数据 D,条件是看不见的网络 A 是一个未知参数。这表现为方框1中的概率 P(D∣A)。可以说,只有当这样的模型被实际阐述时,我们才最终对我们的网络抽象意味着什么以及它与数据的关系有了精确的定义。在决定了生成模型之后,重构网络的推理程序直接来自于后验分布 P(A∣D),由公式(1)给出,以一种有原则的方式。剩下的是与推理的可操作性、效率和可行性有关的理论和技术问题,但不再是其可解释性。估计的不确定性和随后的分析的统计意义是这种方法的自然结果。
在下文中,我们将说明因忽视或避免上述规定而产生的常见陷阱。
(I)基于相关性和阈值的重构。我们认为,不仅要了解网络数据的出处,而且要明确我们希望从中提取的基本抽象,这一点至关重要。也许这个问题最好的系统例子是对时变信号的研究,其中每个节点产生一个时间序列,负责耦合不同节点动态的底层网络结构是未知的,从数据到网络的最短线路是考虑时间序列之间的相关性,作为一个加权的“相关网络”的“边”。然而,最基本的是,相关性与因果关系有根本的不同,在许多情况下观察到的相关性是各单位之间间接因果关系的结果,或者事实上根本没有因果关系。
有人可能会说,尽管不充分,但相关性是因果关系的必要证据,因此识别相关性的模式可能会产生关于潜在因果关系的洞察力。事实上,对于纯粹的观察性数据(即没有能力进行干预),最终可能没有其他选择[63]。然而,天真地对待这个问题是一个值得高度关注的原因。我们用一种有很大缺陷但常用的基于相关性的提取关联的方法来说明这一点,即如果两个时间序列的相关性超过预定的阈值,就认为它们之间存在关联。我们可以通过一个基本的例子看到这种方法是如何失败的。考虑三个变量 X(t)、Y(t) 和 Z(t),它们分别代表时间序列,其中 X(t) 和 Y(t) 只是 Z(t) 的噪声扰动,例如:
其中ϵ1 和 ϵ2 是独立的噪声项。显然,在给定 Z(t) 的情况下,X(t) 和 Y(t) 是有条件独立的,但是 X(t) 和 Y(t) 会有一个非零的相关性,可以超过任何任意的阈值。因此,相关阈值处理将假定在 X(t) 和 Y(t) 之间存在一条边,即使不存在。
然而,尽管这种限制在某些学科中是众所周知的,但在其他学科中却经常被忽视,从而导致了一些基于相关阈值的工作。在图2中,我们用一个在食物网[64]上模拟的伊辛模型的简单例子来说明这种表示方法是多么的不合适。Ising 模型是统计力学中铁磁性的一个简单的数学模型,其中每个节点在给定的时间内处于两种状态 {-1, +1} 中的一种。连边间的相互作用使相邻的节点状态以较大的概率对齐或反对齐。请注意,我们选择伊辛模型进行说明,不是因为它的现实性,而是因为它的简单性和易于解释。在临界温度下从模型中抽取 M=105 个独立样本后,我们计算节点之间的成对相关性,并选择那些高于阈值 t 的节点作为我们暂定的重构网络的边。当 t 的值在整个范围内变化时,所产生的相关网络从未达到与真正的基础网络有多大的相似度。我们在图2中进一步显示,典型的网络描述符根据所选择的阈值有很大的不同。虽然有可能选择一个特定的 t 值,使一个给定的描述符与真实的网络相匹配,但这些特定的值对所有的描述符来说是不一致的。这种不一致性给那些在这种分析基础上选择“最佳阈值”的研究带来了关键问题,因为这种最佳阈值会随着描述符的变化而变化,从而使全局优化的概念失效。即使阈值被选为与真实网络的距离最小——这在实践中是不可能完成的任务,因为真实的网络是不存在的——大多数描述符仍然是严重扭曲的。
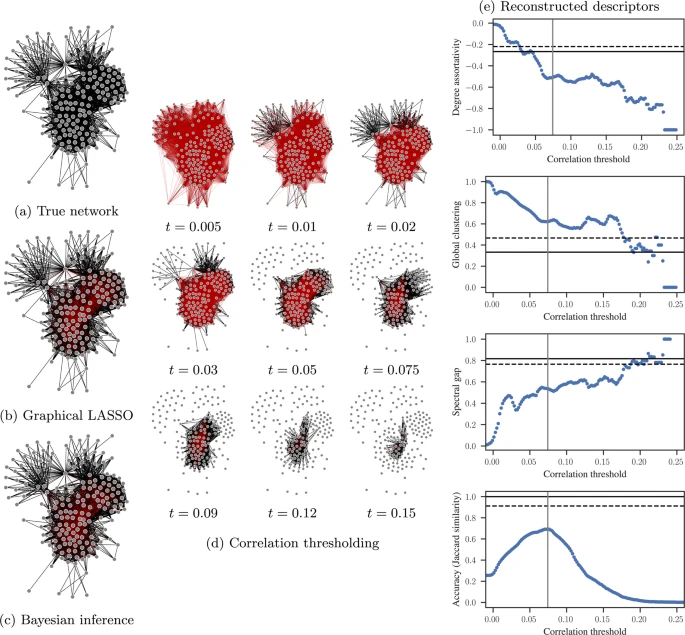
图 2:行动中的网络重构。经验食物网的重构(左上),来自临界温度下伊辛模型的 M=105 个样本。左图:(a)真实的原始网络,与通过使用图形化套索算法( LASSO);(b)推断稀疏精度(反协方差)矩阵得到的重构网络进行比较。在真实网络中不存在的边缘被染成红色。图形化的 LASSO 假设数据来自一个多变量的高斯,这显然是一个错误的规范。然而,即使这个错误的模型也比天真的相关阈值法表现得更好。用参考文献中的贝叶斯方法得到的结果[68],它与数据生成过程相匹配,因此提供了一个更准确的重构,显示在面板(c)。中图:(d)通过将超过阈值 t 的成对相关性视为网络中的边而得到的网络,如图例所示。右图:(e)描述符–从通过相关性阈值处理获得的网络中测得——作为相关性阈值 t 的函数。水平实线标志着为真实网络获得的值,水平虚线标志着用贝叶斯推断获得的值。右下角的图显示了真实网络和重构网络之间的杰卡德相似度(Jaccard index),在所有数字中,垂直线标志着具有最大杰卡德相似度的阈值。
事实上,这个问题的一般解决方案是再次认识到数据(相关性)和抽象(网络)之间的区别,并接受从间接数据推断或重构隐藏网络的观点。这样的想法并不新鲜:早在20世纪70年代,关于多变量分析的文献就把这个问题框定为协方差选择[65],认识到条件独立性可以用精确矩阵(协方差矩阵的逆)中的零来模拟。这方面的一个经典方法是图形化的套索算法[66],它将一组时间序列建模为多变量高斯,并推断出一个与数据一致的稀疏精度矩阵。我们在图2中看到,即使有这种错误的模型,我们也能比天真的相关阈值法更好地重构网络。
我们还可以更进一步,把这个问题放在与公式(1)完全相同的推理框架下,因为它代表了一个非常普遍的重构环境。对于这个问题,数据 D 不是嘈杂的网络测量值,而是代表节点状态随时间演变的一组时间序列,即伊辛模型的样本[67]。这种重构方法已经在参考文献中得到证明[68]。我们在图2中展示了它在我们的例子中是如何表现的,在相同的数据下,它取得了远远优于阈值方法的准确性。这种优越性能的原因是直接的。公式(1)允许我们以一种正式的方式阐明我们对底层网络和数据如何产生的先验知识。公式(1)也给了我们直接从这些信息的组合中得出的推论。如果我们的假设是正确的,那么我们就有了一个可证明的最佳方法,因为没有其他方法能够与之竞争。否则,所产生的推论代表了我们知识的最佳状态,一旦发现更好的假设,就可以用同样的框架将其与之前的假设进行比较。
无论最终设计并使用什么重构程序来代替上述处方(甚至是按原样获取数据的程序),在形式上都等同于一个特定的后验分布,其中隐含的模型规范确实存在,但被隐藏起来,使得它难以表达或分析。然而,它的隐性特征并不能免除它的论证。因此,我们认为,模型规格需要被明确化,这样它们就可以被轻易地判断出来,而不是被保护起来不受审查。
试图绕过这种建模途径没有合理的科学论据,尽管很难或无法详细说明可能的数据生成机制可能证明是一种技术障碍:例如,当时间序列不是来自已知的、可处理的过程,如伊辛模型或脉冲耦合振荡器[69];在这种情况下,任何动力学的生成模型最多只是一种近似,目前的研究挑战包括开发一个通用框架来克服这些限制。一种可能性是尝试与网络本身一起推断动力学,这可能是以非参数方式近似的,例如使用贝叶斯符号回归[70]。
(II)基于接近性的重构。所谓的“邻近网络”提供了网络分析的一个很好的例子,在这种分析中,一个给定的观察被直接映射到一个直接的网络表示,往往绕过了任何潜在的抽象。在这些分析中,有时间标记的边与两个人之间的接近事件相关联,也就是说,当他们的距离超过预先定义的距离阈值或面对面的互动被记录下来的时间点[71-73]。
这些重要的工作使得一系列关于时间网络的研究非常有成效[74],通过提供丰富的可解释的网络数据,在此基础上发展了有意义的理论,以及对网络方法的评估和比较。然而,与“相关网络”类似,重要的是要考虑到这些接近事件可能会或可能不会产生所需的信息,这取决于具体背景。例如,在重构社会关系时,物理上的接近[73]可能不那么有意义。偶然的相遇可能是由于共同的环境而发生的,例如,进入同一个电梯,在食堂吃饭,或共用公共交通工具,这并不表明有意义的社会关系。另一方面,面对面的互动可以排除由于单纯的接近而产生的相遇[72],但它们仍然忽略了互动的背景和性质,超出了它们的时间和持续时间。一个更具挑战性,但可以说更有信息量的方法是阐明我们想考虑的不同种类的潜在配对关系,以及它们如何通过生成模型影响接近事件(例如,与单纯的熟人相比,亲密的朋友在空间和时间上的互动应该有多大不同?) 以这种方式推断这些类型的潜在社会关系将比使用原始空间数据作为主体更适合于大多数社会动力学的分析。
我们强调,对于任何特定的数据来说,没有固有的正确的网络表示,这完全取决于所寻求的答案。事实上,在传染病的传播研究中,临近网络提供了一个很好的表示方法,例如,它主要依赖于身体接触的时间和临近程度,而不依赖于是什么促成了这种临近。精心设计的受控实验中,精心选择和校准的个人传感器,以检测相关物理和时间范围内的接近程度,已被用于重构潜在的传播途径网络,并研究减轻传染的策略的效果[75-83]。然而,即使在这种情况下,所选择的网络表征是令人信服的,人们仍然需要考虑在何种程度上可以从数据中提取。使用异质或未校准的设备,以及环境效应(物体、墙壁、地板等的吸收/反射)扩大了检测到的接近事件和潜在传输之间的差距[84]。适当地选择表示方法永远不会消除对推断步骤的需要,该步骤从数据中提取感兴趣的基本对象,具有一定的不确定性。
(III)基于具体粒度规定的重构。为分析选择相关的时间或空间尺度,也称为粗粒度,是各种应用学科(不仅仅是网络科学)需要解决的另一个无处不在的困难问题。一个给定的尺度选择,或系统中被测量的方面,将不可避免地掩盖较小尺度的信息,或未被测量的方面。因此,基于特定选择的直接网络表示可能只提供了整个系统的不完整或扭曲的画面。
一个很好的例子是空间网络,如城市系统或更大范围内的网络。在这种情况下,偏差的来源是可修改的区域单位问题,当基于点的测量被汇总到限定的地理区域时,就会出现这种问题[85]。考虑到人类移动网络,GPS 数据被用来推断一个城市或一个国家的不同部分之间的流动:点数据被汇总到空间和时间上的一个选定的颗粒度,而没有明确的线索表明必须使用哪个尺度。不幸的是,这种选择会极大地影响重构的网络拓扑结构,将结果限制在这种特定的时空粒度上,不容易对观察到的现象进行概括[86,87]。因此,在以这种方式对空间数据进行粗粒度分析时,必须认识到分辨率的影响,并谨慎地选择适当的分辨率或平行探索多个分辨率。
还有一些例子,相关性和空间粒度的问题甚至可以混合起来。一个典型的例子是重构人脑中的连接。一种方法是通过基于扩散的成像技术来实现[88]。在这种情况下,结构连接是通过像扩散张量成像这样的方法推断出来的,同时用三维建模来表示神经束。使用这种方法,困难在于追踪物体三维图像中的神经束,并汇总几个人的测量结果。由于不同个体的大脑在解剖学上并不完全相同,这就需要使用模板来对大脑进行包裹。这个过程中涉及到的尺度选择,如感兴趣的区域(即节点),有可能会引入一个偏差。输出链路可以代表道的数量或拥有这些道的概率,但所产生的网络将取决于用于建模的具体方法,并再次取决于阈值选择。
另外,所谓“功能连接”的测量是基于大脑区域局部活动的 fMRI 数据。它也依赖于选择一个图集来定义节点,以及选择一种方法来捕捉时间序列之间的相关性,从而有可能由于选择一种方法而引入一种偏见。在这种情况下,连接代表活动的相关性,而不是物理神经束:网络科学家不认为这种连接是有形网络的一部分,而是在某些条件下(如静止状态或任务表现)绘制共同激活的脑区的一种方式。关于更广泛和更专业的讨论,我们参考[89]。
然而,结果是,使用这种启发式方法推断的拓扑信息取决于时间序列的长度,并倾向于高估某些模式[90]。这些被误报的模式对我们理解人脑有非同小可的后果,如人脑的小世界性特征[91],与小包的数量有很大的关系[92]。更具体地说,Papo 等人解决了网络神经科学家如何利用标准的系统级神经影像技术,在大脑功能网络的背景下解释“小世界”构造的问题,而不考虑物理上的人脑本身是否是一个小世界网络,我们参考了他们的工作[91]。
同样,似乎缺乏的是通过生成模型(在任何测量之前)明确阐述什么构成了大脑区域之间的连接,以及这与测量数据的关系。例如,一旦把它作为一个重构问题,推断出的特征与负责观察到的共同激活模式的基础网络有关,那么应用于功能连接的网络模型就是可能的[68,93]。
(IV)基于状态空间和时间相关性的重构。另一种重构方法是把观察到的时间序列看作是一个(未知的)动力学系统的结果,该系统一般可写为:
其中 xi(t) 是大小为 N 的网络中第 i 个单元的状态变量,Fi 编码状态变量及其耦合的非线性函数,ξi(t) 是一个平均值为零的噪声项,x = {x1, x2, . . , xN} 表示系统的状态向量。这种表示方法允许人们将重构任务作为一个逆向问题的解决方案,其中动力学系系统理论提供了一套强大的工具来描述状态空间重构和不变度量方面的基本动力学特征。
也许这种方法最典型的例子来自 Marc Timme 和合作者的工作[94-98]。大体上,这些方法是基于寻找最小的网络(即边缘耦合的最小 ℓp-norm ),该网络与非线性系统(通常是耦合振荡器,但泛化是可能的[99])的未确定的反转相兼容。这种分析方法在动力系统理论和网络重构之间提供了一种揭示性的联系。然而,一个缺点是,它只提供了推断网络的点估计,即没有不确定性评估的单一网络估计。
另一个例子来自于大气动力学的应用,在大气动力学中,数据可以在时空网格上获得,降维和重构的组合被用来测试关于基本机制的假设[100]。另一种应用于极端降雨事件的方法,引入了一种技术,纠正由于多重比较造成的偏差——与建立 Bonferroni 网络[101]的精神相似——并与网络分析相结合,以揭示可能由称为罗斯比波的物理机制控制的全球远程连接模式[102]。最近,发现算法与条件独立性测试的适当结合被用来推断由合成系统和真实世界系统验证的网络,后者是基于气候系统和人类心脏的已知物理机制[103]。
在某些情况下,在假设非线性确定性动力学起作用的情况下,也可以推导出关系,而不需要明确地要求对支配动力学方程的了解[104]。这就是经验动力学模型的情况——容纳非平衡和非线性动力学等理想情况,可用于无方程建模和预测[105],并在网络动力学方面有新的应用[106]——以及其他基于状态空间重构的方法[107]。
由于相互连接的单元的复杂动力学通常可以由一组耦合的 ODE 来描述,其中每个方程由一个编码主体的自我动力学的项,以及一个编码其他主体的影响的项组成,因此可以通过使用完整的正交基来近似解决反问题。按照这个规定,人们可以使用观察到的时间序列来估计模型的未知系数,为每个主体制定一个线性反问题。这种方法在应用于广泛的问题时证明是成功的,从研究小鼠群体的社会同步性到相互依赖的电化学振荡器[108]。
虽然上面提到的方法大大接近我们提出的一般推理程序,但总的来说,它们还没有完全实现。这是因为它们通常避免明确定义生成模型,并试图从时间序列的时间相关性中重构基础网络。尽管这些方法经常被说成是为了发现因果关系,但这实际上是一个错误的说法,也是一个假设一个事件在另一个事件之前可以作为因果关系证明的事后推理谬误的例子。尽管正如我们已经提到的,纯粹从观察数据中完全消除因果关系的希望不大,但一个适当的推理框架将赋予与数据相符的每一组可能的因果关系以同等的后验概率,只要它们在先验中也是同等可能的。这将把数据中存在的因果关系模糊性转化为不确定性估计,这是上述大多数方法所缺乏的,因为它们只产生一个“点估计”,即一个没有相关误差评估的单一网络。
此外,对那些声称“无模型”的重构方法应持一定程度的怀疑态度,因为这可以说是不可能的。这是因为我们可以反向使用公式(1)的贝叶斯公式,从任何推理程序 P(A∣D) 中获得与之兼容的相应生成模型 P(D∣A)。因此,重构方法不可能没有模型;最多只能在方法的技术实现背后将它们遮蔽起来。这种不能轻易检查不可避免的建模假设的情况,必须伴随着任何可以想象的重构方法,使这些所谓的无模型方法成为黑箱,应该小心处理。理想的情况是,建模假设应该明确,以邀请审查、模型选择和科学过程的通常迭代。
(V)基于对扰动的反应的重构。在某些情况下,人们观察一个系统单位的时间过程,但也有机会:(i)用小的扰动作用于系统并记录其动态响应,或者(ii)获取已知扰动发生在空间和时间的特定点的数据。
在这种情况下,可以可靠地总结为受控扰动实验,人们可以开发特别的方法来利用系统的响应来重构未知的拓扑结构。例如,有可能量化弛豫后的渐进响应,此时系统已经达到了一个新的动态平衡状态,可以用响应矩阵[109]来捕捉。这种方法使人们能够捕捉到一个节点对其本地邻域的影响,并在不同的复杂系统中恢复一些明显无处不在的缩放规律,在细胞动力学和在线社交网络的人类动力学中找到应用[110]。
对于特定类型的动力学(例如,流行病传播或信息扩散),扰动可以在每个时间步骤中通过指定一个单元的状态变化来编码,以响应其邻居在先前时间步骤中的相应状态变化。在这种情况下,底层动力学方程可以用典型的易感-感染-易感(SIS)模型来写,通过将重构问题映射到解决一个凸优化问题,如压缩感应[111]。虽然这种方法在其工作假设下是强大的,但它只限于所考虑的动力学系统类别。然而,它提供了一个有希望的程序,可以适用于其他反问题。事实上,将重构问题转化为稀疏信号重构问题的相同技巧可以应用于其他情况,如进化游戏和通信过程,其中另一种凸优化方法,即 LASSO,甚至可以用于存在噪声的时间序列和部分缺失的节点数据[112]。
另一种可能性是利用充分驱动信号的不变措施的反应来重构系统单元之间的物理相互作用。在温和的假设下,可以证明平均驱动信号的矢量可以与响应差异和基本动力学的雅可比矩阵(Jacobian matrix)直接相关。受控扰动实验的数量越多,重构的精度就越高。然而,往往实现许多这样的实验是不现实的:为此,人们可以利用压缩感知来寻找相应的优化问题的解决方案,在重构经验网络方面取得显著的准确性,如果蝇的昼夜钟网络[97]。这种技术很强大,但其性能可能关键取决于可用实验的数量。
许多网络科学技术的核心是计算网络描述符,如度分布、聚类、中心性、最大模块化[1]。收集这些描述符的目的是,它们可以对网络的特性进行有意义的总结,比如根据某种重要性的衡量标准来确定有影响力的节点,或者描述小规模和中规模的结构。
然而,以黑箱方式使用描述符的情况并不少见,没有充分考虑它们的原始背景、局限性和可解释性,只是简单地提出,很少讨论报告值的含义。这种对网络描述符的漫不经心的应用意味着,即使我们理解了某个描述符所测量的内容,该描述符在特定的背景下也可能无法提供有意义的信息。例如,一个描述符可能会因为基本的统计数据而失去适用性,比如当我们用平均度数来总结度数分布时,尽管前者是重尾的,从而使平均度数没有代表性。不适用性也会由于基本的解释问题而发生,例如,当描述符(如最短路径)应用于边缘代表统计相关性或概率的网络时,不再具有相同的意义。
在下文中,我们将强调当网络描述符以不恰当的方式被使用时出现的一些常见问题。
(I)制定零模型和测试假设。有些描述符衡量的是随机零模型的平均值的偏差,比如模块度[113]——衡量网络被组织成同种社区的倾向,以及富人俱乐部系数[114]——衡量高度联系的节点相互连接的倾向。因此,这些描述符有一些假设(即零模型的假设),这些假设几乎肯定不会是普遍适用的,而且常常被忽视。
这些网络描述符取决于具体背景,因此不能直接解释其绝对值,例如,一个最大模块化为 Q=0.9 的网络不一定比另一个 Q=0.6 的网络有更强的社区结构(事实上,即使是完全随机的网络也可以有高的模块度值[115])。因此,通常有必要将观察到的数值与明确说明和适当选择的零模型下的数值分布进行对比。以这种方式使用零模型需要决定网络中的哪些元素应该是随机的,但如何做出这个决定在很大程度上仍然是一个开放的问题。回答这个问题的关键是确定网络的哪些属性对给定的问题很重要,因此需要固定,哪些属性可以改变。例如,为了确定一个特定的节点特征是否与网络结构有关,我们看到了一些例子,这些例子是基于将网络统计量与空分布进行比较,这些空分布要么是固定网络结构并改变节点特征[116,117],要么是固定度分布并重新连接链接[118],或者是两者的组合[119]。目前还不清楚在给定的情况下,我们应该选择哪种零模型。在许多情况下,试图说出网络不是什么(即选择一个零模型)不能完全与关于网络可能是什么(即生成模型)的假设脱钩,因此,试图将第一种方法作为完全绕过第二种目标的手段通常是命途多舛。
此外,虽然针对零模型的测试可以是很好的做法,当它允许我们很容易地排除缺乏特定兴趣属性的明确定义的场景时,我们可以说,只要我们试图从数据中提取的答案需要超过一个单一的标量值,它就会从根本上被误导。当我们试图拒绝一个零模型时,我们只能回答哪个模型对数据不负责任的问题。当我们的假设涉及详细的多维结构时,这个答案充其量是不相关的。在最坏的情况下,它诱发了一个严重但常见的误解,即没有证据证明零模型意味着有另一个没有被明确检验的假说存在的证据。这种错误的一个突出例子是使用模块度最大化的社区检测120。尽管这种非统计学方法的许多严重缺点早已在理论和方法学论文中得到确认和研究[115,121-123],但模块度最大化仍然被广泛采用,特别是在特定领域的应用中。虽然模块化值本身衡量的是对零模型的偏离,但当它被最大化时,它不具备统计学上的正则化,因此它甚至在完全随机的图中也能找到高分的分区,这完全是由于随机波动[115,124]。这导致许多研究人员建议计算模块度的统计意义,当与完全随机网络的零模型相比时[125]。然而,不难看出,以这种方式来构思问题其实是不合适的。我们在图3中说明了这一点,我们展示了一个完全随机的图,增加了几条非随机的边,形成了一个由 6 个节点组成的嵌入式完全子图。尽管非常小,但考虑到零模型,对网络的这种修改是非常不可能的,因此它导致最大模块化的值大大偏离了从零模型得到的值。因此,当遇到这样的网络时,我们会自信地得出结论——正确的结论——完全随机网络的零模型应该被拒绝,正如我们在图3a中看到的那样。然而,这并不意味着所发现的社区结构——节点的实际划分——在统计上是有意义的。我们可以通过检查发现的实际分区看到这一点,如图3b所示。我们看到,尽管模块化的高分值对应于在某种程度上被识别的社区的分区,但它也发现了许多与网络背后的实际生成过程无关的其他社区,也就是说,它们代表了直接由零模型的随机性产生的密度波动[126]。
图3:用零模型和生成模型评估群落结构。(a)N=100 个节点的完全随机网络的零模型的最大模块化值 Q 的分布。垂直线标志着该网络的修改版本所遇到的数值,如文中所述,该网络有一个嵌入的 6 个节点的完全子图。
上述答案之所以不合适,是因为我们问错了问题:模块化的最大值是否具有统计学意义基本不重要,重要的是发现的分区在多大程度上可以归因于零模型。要回答这个问题,实际上把它翻过来,并试图确定哪个模型更有可能对数据负责,而不是哪个零模型应该被拒绝,这样做会更有成效。这种想法构成了基于随机区块模型(SBM)[126-129]的现代推理方法的主干,它为每个可能的网络分区 b 赋予了一个后验概率:
其中 P(A∣b) 是 SBM 的可能性,这是一个考虑到网络模块化结构的网络结构生成模型。正如我们在图3c中看到的,当应用于同一个网络时,这种方法不仅可以完美地识别出完全子图,而且还可以正确地确定其余的节点属于同一个分区,也就是说它们都有相同的概率连接到网络的其他部分。这种方法效果更好,因为它相当于问了一个更合适的基本问题:网络最可能被分成的组是什么?除了通过公式(4)之外,不可能以任何其他方式回答这个问题;尽管我们可以以许多方式选择其部分[129]。顺便提一下,用这种方法我们也能比通过模块化更明确地拒绝完全随机网络的零模型。原因是完全随机的网络相当于具有单一组的 SBM 的一个特例,对于它我们能够写出一个精确的后验概率。然而,尽管这种方法在概念上、理论上和实践上都有优势,但它还没有达到某些应用领域。
通过问自己为什么这些方法没有渗透到网络科学的全部领域,我们可以找出一些可能性。一个特别的问题是,研究人员受制于寻找下一个重大突破的动机,而不是探索现有方法之间的等价性[130,131],或者重新审视先前的工作或既定的信念(例如,节点属性不是真正的社区[132],网络数据是不确定的[43],阈值化相关矩阵是徒劳的[65]),并可能重新发明车轮[133]。社区检测提供了一个特殊的案例,因为 SBM 最早是在几十年前开发的[134,135](尽管其推断的稳健和有效的方法是在过去十年才开发的)。自从引入社群检测问题[136]以来,我们看到了大量的方法被开发出来,造成了理论上的不一致。一个不幸的结果是,这些方法中有许多可以被看作是 SBM 框架原则性较低的变种或近似[130]。这种对问题空间的特定部分的过度探索,几乎肯定是以忽视网络聚类的其他相关问题为代价的[126,137]。
(II)对重构不确定性的考虑。还有一些实际情况,人们对数据提出了错误的问题。由于任何现实世界的测量都会受到测量误差的影响,所以在估计网络描述符时,应该考虑到它们以及它们的传播,这是标准的做法。这将使我们能够量化我们估计的不确定性,并在不同的测量和实验中比较结果,就像任何定量学科一样。相反,如果缺乏这样一个合适的程序,就不可避免地导致无法在不同的实验中进行比较的估计,从而导致不容易解决的矛盾结果。
让我们再考虑一下这样的情况:底层网络结构不为人知,但有可能从节点上测量一些信号(见图4)。很多时候,相关或因果分析被用来表示系统单元之间的功能关系,并从这种表示中连续计算网络描述符。
图4:在不确定性下测量网络描述符。在许多实际问题中,网络的结构无法直接观察,而信号(如物理变量的时间过程)可以从其单元中测量。在应用了第二节中描述的有效的重构方法后,结果可以通过每个成对链接存在的边际概率以一种方便的方式进行总结,代价是损失了全部联合分布中的一些信息。请注意,这些概率的集合并不代表一个加权或有向网络,在相应的图上进行任何标准的网络分析都是错误的。事实上,在这种情况下,单个节点或整个网络层面的单一测量被概率分布所取代,编码测量一个特定值的可能性。例如,在一个大小为 N 的网络中,代替单个节点 i 的度数 ki 的是估计该节点具有度数k的概率 P(ki = k),k = 0,1,…,N。同样地,节点 i 的跨度 ci 被替换为该节点具有跨度 c 的概率 P(ci = c),这可能对应于多个局部配置而不是一个特定的配置,如图中右侧所示。这种概率分布可以在用于建立概率网络模型的贝叶斯推理框架内得到[106]。
在应用有效的重构方法后,如第(II)节所述,也有可能以一种方便的方式总结节点 i 和 j 之间存在边缘的边际概率 pij,以现有的数据为条件,以损失完整联合分布中的一些信息为代价。这个步骤在某些情况下可能是必要的,例如,当一个合理的动力学模型还不清楚的时候。
其结果是一个概率网络,但不能简单地作为一个传统的网络来分析,因为概率并不代表传统的权重。请注意,在所考虑的情况下,概率网络模型是任何有效的重构方法的结果:没有办法将从统计程序测得的链接升级为真正的链接。
在这种情况下,没有一个网络描述符可以只用一个数字来正确表示。例如,让我们考虑度,这是最简单的节点中心性测量,它计算其传入和传出链接的数量。如果每个链接都有一定的概率存在,那么度本身就成为一个随机变量,需要一个概率分布来描述。因此,例如,报告 i 的度数等于3,对于从其单元信号的观察中重构的系统来说是没有意义的:相反,评估节点 i 的度数为 3 的概率等于 10% 或者评估它在一个置信区间或可信区间内为 3 是有意义的。虽然这种评估对统计学家来说可能显得很自然,但它仍然被忽视了。促进这种估计的方法仍然没有得到很好的发展,只是在最近才出现[106],主要集中在特定的问题上,如耦合振荡器的网络[138],通过使用随机矩阵理论[139]重新定义零模型或提出能够保留节点强度的特殊配置模型[140]。然而,基于贝叶斯推理的重构提供了一个优雅而统一的框架,也自然而然地使我们能够满足这种要求。
网络科学的巨大前景建立在数十年来各学科为发展共同语言所做的共同努力之上,同时也伴随着进一步推进这种语言的责任,使之超越每个学科孤立的内在有限视角。巩固网络科学的好处并不局限于它自己的社区:事实上,要求加强方法论标准会催化不同学科之间的交叉融合。
因此,在不久的将来,重要的是不要忽视对严格的理论和方法的需求,对它们的谨慎应用,以及对其结果的谨慎解释。网络科学不是构建任意的网络和计算网络统计数据的表格。相反,它应该是一个全面的框架,可以增加价值,让我们测试新的假设,确定新的见解和解释:方法和应用已经并将继续塑造网络科学。
为了充分实现其潜力,必须通过承认网络科学的跨学科性质来维护和加强方法与应用之间的联系。收集来自广泛背景的科学家,为思想的交叉融合提供了巨大的机会,但这只有在我们都相互理解的情况下才会奏效。为了加强理论和应用之间的联系,我们必须建立一个共同的认识论理解,反映在我们的方法论和共同语言中。我们还应该警惕简单地将一个领域的术语移植到另一个领域,例如,网络社区不一定意味着社会或生态社区[117],网络可控性不一定意味着我们可以进行精神控制[141]。
展望未来,我们需要对我们在应用网络方法时做出的选择进行更多的批判性思考。网络科学是一门相对年轻的学科,但它是建立在数学、物理学和计算机科学等成熟的方法论学科以及它所采用的所有应用领域的坚实基础之上的。随着它走向成熟的新阶段,该领域需要巩固最佳实践,就像其他成熟领域所发生和继续发生的一样。例如,最好避免纯粹的启发式(重新)构建网络和不谨慎地应用网络统计,要遵循本工作中讨论的那些良好做法。
尽管听起来很有吸引力,我们可以把这么多复杂的系统表现为网络,以利用一套通用的工具,但最终我们应该远离创造一刀切的解决方案。相反,我们应该更紧密地合作,开发严格的方法,纳入相关的领域知识,并允许我们更深入地探究和直接解决那些只有通过将系统视为一个整体才能回答的问题。
在这里,我们展示了生成模型是如何为实现这些共同目标提供有希望的手段的。生成模型是可扩展的,可以很容易地适应于明确编码关于复杂系统和我们如何观察它们的特定假设和假定。统计推理使我们能够拟合这些模型,并比较对竞争假设的支持程度。以这种方式开发端到端的模型,承认了网络分析的过程,从数据到结论,本身就是一个复杂的系统。分析过程中的任何阶段都是独立的,因此不应该被孤立地处理。我们在整个分析过程中的设计决定应该是相互联系的,这样,具体的选择可以相互参考[54,68,93,142]。
基于我们的分析,我们可以为网络科学的下一步发展及其对特定领域挑战的应用确定一套简洁的最佳实践。首先,我们必须了解网络数据的出处,并通过生成模型,明确希望从其中提取的基本抽象。理想情况下,我们选择的抽象不应该依赖于空间和/或时间粒度的任意选择,或者我们至少应该证明所产生的分析对这种选择不敏感。第二,我们必须在理论上和实践中纳入网络测量中的错误和不完整的存在和影响。第三,当开发一个新的分析方法时,我们应该在合成数据上验证它,以保证找到预期的结果。如果一种方法的有效性不能在受控的合成实验中得到证明,那么当它被应用于经验数据时得到的结果就没有什么价值。
在特定经验科学领域的研究人员眼里,我们所讨论的大部分内容可能看起来是标准和既定的准则。我们在这里强调的是,如果不更普遍地采用严格的方法论,就会出现一些微妙的问题。网络科学界的特点是其成员的异质性背景,这是我们社区的优势之一。然而,这种异质性也意味着,上述的许多观点,作为一个整体,并没有得到普遍的认可,因此需要强调。例如,在特定学科范围内容易识别的方法学缺陷,即使应用于相同的数据,在更广泛的网络科学范围内,也不可避免地会导致有争议的结果。因此,有必要超越个别学科的特定语言和实践,积极地进行交叉授粉,以便在我们的多学科领域获得一个共同的最佳实践标准。
只有在负责任地使用并具有适当水平的方法论严谨性的情况下,网络科学的工具才能让我们对复杂系统的结构、功能和动力学有独特的洞察力。
-
Newman, M. E. J. The structure and function of complex networks. SIAM Rev.45, 167–256 (2003).
-
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M. & Hwang, D. U. Complex networks: Structure and dynamics. Phys. Reports.424, 175–308 (2006).
-
Guimerá, R. & Nunes Amaral, L. A. Functional cartography of complex metabolic networks. Nature433, 895–900 (2005).
-
Yu, H. et al. High-quality binary protein interaction map of the yeast interactome network. Science (New York, N.Y.)322, 104–110 (2008).
-
Costanzo, M. et al. The genetic landscape of a cell. Science327, 425–431 (2010).
-
Bassett, D. S. et al. Dynamic reconfiguration of human brain networks during learning. Proc. National Acad. Sci.108, 7641–7646 (2011).
-
Bullmore, E. & Sporns, O. The economy of brain network organization. Nat. Rev. Neurosci.13, 336–349 (2012).
-
de Vico Fallani, F., Richiardi, J., Chavez, M. & Achard, S. Graph analysis of functional brain networks: practical issues in translational neuroscience. Philosophical Transactions Royal Society B: Biological Sci.369, 20130521 (2014).
-
Bascompte, J., Jordano, P. & Olesen, J. M. Asymmetric coevolutionary networks facilitate biodiversity maintenance. Science312, 431–433 (2006).
-
Ings, T. C. et al. Ecological networks–beyond food webs. J. Animal Ecol.78, 253–269 (2009).
-
Pilosof, S., Porter, M. A., Pascual, M. & Kéfi, S. The multilayer nature of ecological networks. Nat. Ecol. Evolution.1, 1–9 (2017).
-
Rosato, V. et al. Modelling interdependent infrastructures using interacting dynamical models. Int. J. Critical Infra.4, 63–79 (2008).
-
Buldyrev, S. V., Parshani, R., Paul, G., Stanley, H. E. & Havlin, S. Catastrophic cade of failures in interdependent networks. Nature464, 1025–1028 (2010).
-
Pastor-Satorras, R., Vázquez, A. & Vespignani, A. Dynamical and correlation properties of the internet. Phys. Rev. lett.87, 258701 (2001).
-
Mahadevan, P. et al. The internet as-level topology: three data sources and one definitive metric. ACM SIGCOMM Computer Communication Rev.36, 17–26 (2006).
-
Watts, D. J. A simple model of global cades on random networks. Proc. National Academy Sci.99, 5766–5771 (2002).
-
Kossinets, G. & Watts, D. J. Empirical analysis of an evolving social network. Science311, 88–90 (2006).
-
Fowler, J. H. & Christakis, N. A. Cooperative behavior cades in human social networks. Proc. National Acad. Sci.107, 5334–5338 (2010).
-
Stella, M., Ferrara, E. & De Domenico, M. Bots increase exposure to negative and inflammatory content in online social systems. Proc. National Acad. Sci.115, 12435–12440 (2018).
-
Silk, M. J., Finn, K. R., Porter, M. A. & Pinter-Wollman, N. Can multilayer networks advance animal behavior research? Trends Ecol. Evolution.33, 376–378 (2018).
-
Cai, W., Snyder, J., Hastings, A. & D’Souza, R. M. Mutualistic networks emerging from adaptive niche-based interactions. Nat. Commun.11, 1–10 (2020).
-
Christakis, N. A. & Fowler, J. H. The spread of obesity in a large social network over 32 years. New England J. Medicine.357, 370–379 (2007).
-
Gallotti, R., Valle, F., taldo, N., Sacco, P. & De Domenico, M. Assessing the risks of ?infodemics? in response to covid-19 epidemics. Nat. Human Behaviour.4, 1285–1293 (2020).
-
Montoya, J. M., Pimm, S. L. & Solé, R. V. Ecological networks and their fragility. Nature442, 259–264 (2006).
-
Bastolla, U. et al. The architecture of mutualistic networks minimizes competition and increases biodiversity. Nature458, 1018–1020 (2009).
-
Pocock, M. J., Evans, D. M. & Memmott, J. The robustness and restoration of a network of ecological networks. Science335, 973–977 (2012).
-
Goh, K. I. et al. The human disease network. Proc. National Acad. Sci.104, 8685 (2007).
-
Vidal, M., Cusick, M. E. & Barabási, A.-L. Interactome networks and human disease. Cell144, 986–998 (2011).
-
Halu, A., De Domenico, M., Arenas, A. & Sharma, A. The multiplex network of human diseases. NPJ Systems Biol. Applications.5, 1–12 (2019).
-
Keeling, M. J. & Eames, K. T. Networks and epidemic models. J. Royal Society Interf.2, 295–307 (2005).
-
Colizza, V., Barrat, A., Barthélemy, M. & Vespignani, A. The role of the airline transportation network in the prediction and predictability of global epidemics. Proc. National Acad. Sci.103, 2015–2020 (2006).
-
Balcan, D. et al. Multiscale mobility networks and the spatial spreading of infectious diseases. Proc. National Acad. Sci.106, 21484–21489 (2009).
-
Gómez-Gardenes, J., Soriano-Panos, D. & Arenas, A. Critical regimes driven by recurrent mobility patterns of reaction–diffusion processes in networks. Nat. Phys.14, 391–395 (2018).
-
Zhang, J. et al. Changes in contact patterns shape the dynamics of the covid-19 outbreak in china. Science368, 1481–1486 (2020).
-
Arenas, A. et al. Modeling the spatiotemporal epidemic spreading of covid-19 and the impact of mobility and social distancing interventions. Phys. Rev. X.10, 041055 (2020).
-
Butts, C. T. Network inference, error, and informant (in)accuracy: a Bayesian approach. Social Networks.25, 103–140 (2003).
-
Young, J.-G., Valdovinos, F. S. & Newman, M. E. J. Reconstruction of plant-pollinator networks from observational data. Nat. Commun.12, 3911 (2021).
-
Zachary, W. W. An Information Flow Model for Conflict and Fission in Small Groups. J. Anthropological Res.33, 452–473 (1977).
-
Morstatter, F., Pfeffer, J., Liu, H. & Carley, K.Is the sample good enough? comparing data from Twitter’s streaming api with Twitter’s firehose. In Proc. of the International AAAI Conference on Web and Social Media, vol. 7 (2013).
-
Mislove, A., Lehmann, S., Ahn, Y.-Y., Onnela, J.-P. & Rosenquist, J.Understanding the demographics of Twitter users. In Proc. of the International AAAI Conference on Web and Social Media, vol. 5 (2011).
-
Moody, J. Peer influence groups: identifying dense clusters in large networks. Social Networks.23, 261–283 (2001).
-
Adamic, L. A. & Glance, N.The political blogosphere and the 2004 U.S. election: divided they blog. In Proceedings of the 3rd international workshop on Link discovery, LinkKDD ’05, 36-43 (ACM, New York, NY, USA, 2005).
-
Goldberg, D. S. & Roth, F. P. Assessing experimentally derived interactions in a small world. Proc. National Acad. Sci.100, 4372–4376 (2003).
-
Lü, L. & Zhou, T. Link prediction in complex networks: A survey. Physica A: Statistical Mechanics Applications.390, 1150–1170 (2011).
-
Watts, D. J. & Strogatz, S. H. Collective dynamics of ’small-world’ networks. Nature393, 409–10 (1998).
-
Taskar, B., Wong, M.-F., Abbeel, P. & Koller, D. Link prediction in relational data. Adv. Neural Inform. Proc. Sys.16, 659–666 (2003).
-
Popescul, A. & Ungar, L. H.Statistical relational learning for link prediction. In IJCAI workshop on learning statistical models from relational data, vol. 2003 (Citeseer, 2003).
-
Guimerá, R. & Sales-Pardo, M. Missing and spurious interactions and the reconstruction of complex networks. Proc. National Acad. Sci.106, 22073 –22078 (2009).
-
Clauset, A., Moore, C. & Newman, M. E. J. Hierarchical structure and the prediction of missing links in networks. Nature453, 98–101 (2008).
-
Airoldi, E. M., Blei, D. M., Fienberg, S. E. & Xing, E. P. Mixed Membership Stochastic Blockmodels. J. Mach. Learn. Res.9, 1981–2014 (2008).
-
Liben-Nowell, D. & Kleinberg, J. The link-prediction problem for social networks. J. American Society Inform. Sci. Technol.58, 1019–1031 (2007).
-
Newman, M. E. J. Network structure from rich but noisy data. Nat. Phys.14, 542–545 (2018).
-
Peixoto, T. P. Reconstructing Networks with Unknown and Heterogeneous Errors. Phys. Rev. X.8, 041011 (2018).
-
Young, J.-G., Cantwell, G. T. & Newman, M. E. J.Robust Bayesian inference of network structure from unreliable data. arXiv:2008.03334 [physics, stat] (2020).
-
Newcombe, H. B., Kennedy, J. M., Axford, S. & James, A. P. Automatic linkage of vital records. Science130, 954–959 (1959).
-
Fellegi, I. P. & Sunter, A. B. A theory for record linkage. J. American Statistical Association.64, 1183–1210 (1969).
-
Pasula, H., Marthi, B., Milch, B., Russell, S. J. & Shpitser, I.Identity uncertainty and citation matching. In Advances in neural information processing systems15, 1425–1432 (2003).
-
McCallum, A. & Wellner, B. Conditional models of identity uncertainty with application to noun coreference. Adv. Neural Inform. Process. sys.17, 905–912 (2004).
-
Dong, X., Halevy, A. & Madhavan, J.Reference reconciliation in complex information spaces. In Proc.of the 2005 ACM SIGMOD international conference on Management of data, 85–96 (2005).
-
Butts, C. T.Revisiting the Foundations of Network Analysis. Science. https://www.science.org/doi/abs/10.1126/science.1171022. (2009). American Association for the Advancement of Science.
-
Whitney, H. Congruent graphs and the connectivity of graphs. American J. ematics.54, 150–168 (1932).
-
Harary, F. & Norman, R. Z. Some properties of line digraphs. Rendiconti del Circolo Matematico di Palermo9, 161–168 (1960).
-
Pearl, J. Causality: Models, Reasoning and Inference (Cambridge University Press, Cambridge, U.K.; New York, 2009), 2nd edition edn.
-
Ulanowicz, R. E. & DeAngelis, D. L.Network analysis of trophic dynamics in south florida ecosystems. US Geological Survey Program on the South Florida Ecosystem 114 (2005). http://sofia.usgs.gov/projects/atlss/atlssabsfrsf.html.
-
Dempster, A. P. Covariance selection. Biometrics157-175 (1972).
-
Friedman, J., Hastie, T. & Tibshirani, R. Sparse inverse covariance estimation with the graphical lasso. Biostatistics9, 432–441 (2008).
-
Nguyen, H. C., Zecchina, R. & Berg, J. Inverse statistical problems: from the inverse Ising problem to data science. Adv. Phys.66, 197–261 (2017).
-
Peixoto, T. P. Network Reconstruction and Community Detection from Dynamics. Phys. Rev. Lett.123, 128301 (2019).
-
Rosenblum, M. et al. Reconstructing networks of pulse-coupled oscillators from spike trains. Phys. Rev. E.96, 012209 (2017).
-
Guimerá, R. et al. A Bayesian machine scientist to aid in the solution of challenging scientific problems. Sci. Adv.6, eaav6971 (2020).
-
Eagle, N. & (Sandy) Pentland, A. Reality Mining: Sensing Complex Social Systems. Personal Ubiquitous Comput. 10, 255–268 (2006).
-
Cattuto, C. et al. Dynamics of Person-to-Person Interactions from Distributed RFID Sensor Networks. PLOS ONE.5, e11596 (2010).
-
Stopczynski, A. et al. Measuring Large-Scale Social Networks with High Resolution. PLOS ONE.9, e95978 (2014). Publisher: Public Library of Science.
-
Holme, P. & Saramäki, J. Temporal networks. Phys. Reports.519, 97–125 (2012).
-
Gemmetto, V., Barrat, A. & Cattuto, C. Mitigation of infectious disease at school: targeted class closure vs school closure. BMC Infect. Dis.14, 695 (2014).
-
Voirin, N. et al. Combining High-Resolution Contact Data with Virological Data to Investigate Influenza Transmission in a Tertiary Care Hospital. Infect. Control Hospital Epidemiol.36, 254–260 (2015).
-
Fournet, J. & Barrat, A. Epidemic risk from friendship network data: an equivalence with a non-uniform sampling of contact networks. Sci. Reports.6, 24593 (2016).
-
Fournet, J. & Barrat, A. Estimating the epidemic risk using non-uniformly sampled contact data. Sci. Reports.7, 9975 (2017).
-
Sapienza, A., Barrat, A., Cattuto, C. & Gauvin, L. Estimating the outcome of spreading processes on networks with incomplete information: A dimensionality reduction approach. Phys. Rev. E.98, 012317 (2018).
-
Ciaperoni, M. et al. Relevance of temporal cores for epidemic spread in temporal networks. Sci. Reports.10, 12529 (2020).
-
Cencetti, G. et al. Digital proximity tracing on empirical contact networks for pandemic control. Nat. Commun.12, 1655 (2021).
-
Barrat, A., Cattuto, C., Kivelä, M., Lehmann, S. & Saramäki, J. Effect of manual and digital contact tracing on COVID-19 outbreaks: a study on empirical contact data. J. Royal Society Interface.18, 20201000 (2021).
-
Colosi, E. et al. Screening and vaccination against COVID-19 to minimise school closure: a modelling study. Lancet Infect. Dis. 22,977–989 (2022).
-
Leith, D. J. & Farrell, S. Coronavirus Contact Tracing: Evaluating The Potential Of Using Bluetooth Received Signal Strength For Proximity Detection (2020). Number: arXiv:2006.06822 arXiv:2006.06822 [cs, eess].
-
Gehlke, C. E. & Biehl, K. Certain effects of grouping upon the size of the correlation coefficient in census tract material. J. American Statistical Association.29, 169–170 (1934).
-
Gallotti, R., Bazzani, A., Degli Esposti, M. & Rambaldi, S. Entropic measures of individual mobility patterns. J. Statistical Mechanics: Theory Experiment.2013, P10022 (2013).
-
Gallotti, R., Louf, R., Luck, J.-M. & Barthelemy, M. Tracking random walks. J. Royal Society Interface.15, 20170776 (2018).
-
Fornito, A., Zalesky, A. & Bullmore, E. Fundamentals of Brain Network Analysis (Academic Press, Amsterdam; Boston, 2016), reprint edition edn.
-
Korhonen, O., Zanin, M. & Papo, D. Principles and open questions in functional brain network reconstruction. Human Brain Mapping.42, 3680–3711 (2021).
-
Zanin, M., Belkoura, S., Gomez, J., Alfaro, C. & Cano, J. Topological structures are consistently overestimated in functional complex networks. Sci. Reports.8, 1–9 (2018).
-
Papo, D., Zanin, M., Martínez, J. H. & Buldú, J. M. Beware of the small-world neuroscientist! Front. Human Neurosci.10, 96 (2016).
-
Arslan, S. et al. Human brain mapping: A systematic comparison of parcellation methods for the human cerebral cortex. NeuroImage170, 5–30 (2018).
-
Hoffmann, T., Peel, L., Lambiotte, R. & Jones, N. S. Community detection in networks without observing edges. Sci. Adv.6, eaav1478 (2020).
-
Timme, M. Revealing Network Connectivity from Response Dynamics. Phys. Rev. Lett.98, 224101 (2007).
-
Shandilya, S. G. & Timme, M. Inferring network topology from complex dynamics. New J. Phys.13, 013004 (2011).
-
Timme, M. & adiego, J. Revealing networks from dynamics: an introduction. J. Physics A: ematical Theoretical.47, 343001 (2014).
-
Nitzan, M., adiego, J. & Timme, M. Revealing physical interaction networks from statistics of collective dynamics. Sci. Adv.3, e1600396 (2017).
-
adiego, J., Maoutsa, D. & Timme, M. Inferring Network Connectivity from Event Timing Patterns. Phys. Rev. Lett.121, 054101 (2018).
-
adiego, J., Nitzan, M., Hallerberg, S. & Timme, M. Model-free inference of direct network interactions from nonlinear collective dynamics. Nat. Commun.8, 2192 (2017).
-
Runge, J. et al. Identifying causal gateways and mediators in complex spatio-temporal systems. Nat. Commun.6, 8502 (2015).
-
Tumminello, M., Micciche, S., Lillo, F., Piilo, J. & Mantegna, R. N. Statistically validated networks in bipartite complex systems. PloS one6, e17994 (2011).
-
Boers, N. et al. Complex networks reveal global pattern of extreme-rainfall teleconnections. Nature566, 373–377 (2019).
-
Runge, J., Nowack, P., Kretschmer, M., Flaxman, S. & Sejdinovic, D. Detecting and quantifying causal associations in large nonlinear time series datasets. Sci. Adv.5, eaau4996 (2019).
-
Harnack, D., Laminski, E., Schünemann, M. & Pawelzik, K. R. Topological Causality in Dynamical Systems. Phys. Rev. Lett. 119, 098301(2017).
-
Ye, H. et al. Equation-free mechanistic ecosystem foreting using empirical dynamic modeling. Proc. National Acad. Sci. United States of America112, E1569–76 (2015).
-
Raimondo, S. & De Domenico, M. Measuring topological descriptors of complex networks under uncertainty. Phys. Rev. E.103, 022311 (2021).
-
Stavroglou, S. K., Pantelous, A. A., Stanley, H. E. & Zuev, K. M. Unveiling causal interactions in complex systems. Proc. Natl. Acad. Sci.117, 7599–7605. http://www.pnas.org/lookup/doi/10.1073/pnas.1918269117 (2020).
-
Wang, S. et al. Inferring dynamic topology for decoding spatiotemporal structures in complex heterogeneous networks. Proc. National Acad. Sci. United States of America115, 9300–9305 (2018).
-
Barzel, B. & Barabási, A.-L. Universality in network dynamics. Nature Physics advance online publication http://www.nature.com/nphys/journal/vaop/ncurrent/full/nphys2741.html (2013).
-
Barzel, B., Liu, Y.-Y. & Barabási, A.-L. Constructing minimal models for complex system dynamics. Nat. Commun.6, 1–8 (2015).
-
Shen, Z., Wang, W.-X., Fan, Y., Di, Z. & Lai, Y.-C. Reconstructing propagation networks with natural diversity and identifying hidden sources. Nat. Commun.5, 4323 (2014).
-
Han, X., Shen, Z., Wang, W.-X. & Di, Z. Robust reconstruction of complex networks from sparse data. Phys. Rev. lett.114, 028701 (2015).
-
Newman, M. E. J. & Girvan, M. Finding and evaluating community structure in networks. Phys. Revi E.69, 026113 (2004).
-
Zhou, S. & Mondragón, R. J. The rich-club phenomenon in the internet topology. IEEE Commun. Lett.8, 180–182 (2004).
-
Guimerá, R., Sales-Pardo, M. & Amaral, L. A. N. Modularity from fluctuations in random graphs and complex networks. Phys. Rev. E.70, 025101 (2004).
-
Bianconi, G., Pin, P. & Marsili, M. Assessing the relevance of node features for network structure. Proc. National Acad. Sci.106, 11433–11438 (2009).
-
Peel, L., Larremore, D. B. & Clauset, A. The ground truth about metadata and community detection in networks. Sci. Adv.3, e1602548 (2017).
-
Ehrhardt, B. & Wolfe, P. J. Network modularity in the presence of covariates. Siam Rev.61, 261–276 (2019).
-
Cinelli, M., Peel, L., Iovanella, A. & Delvenne, J.-C. Network constraints on the mixing patterns of binary node metadata. Phys. Rev. E.102, 062310 (2020).
-
Fortunato, S. Community detection in graphs. Phys. Reports.486, 75–174 (2010).
-
Fortunato, S. & Barthélemy, M. Resolution limit in community detection. Proc. National Acad. Sci.104, 36–41 (2007).
-
Good, B. H., de Montjoye, Y.-A. & Clauset, A. Performance of modularity maximization in practical contexts. Phys. Rev. E.81, 046106 (2010).
-
Ghasemian, A., Hosseinmardi, H. & Clauset, A. Evaluating Overfit and Underfit in Models of Network Community Structure. IEEE Transactions on Knowledge and Data Engineering1-1 (2019).
-
McDiarmid, C. & Skerman, F. Modularity in random regular graphs and lattices. Electronic Notes in Discrete ematics.43, 431–437 (2013).
-
Reichardt, J. & Bornholdt, S. When are networks truly modular? Physica D: Nonlinear Phenomena.224, 20–26 (2006).
-
Peixoto, T. P. Descriptive vs. inferential community detection: pitfalls, myths and half-truths. arXiv:2112.00183 [physics, stat] (2022). ArXiv: 2112.00183.
-
Karrer, B. & Newman, M. E. J. Stochastic blockmodels and community structure in networks. Phys. Rev. E.83, 016107 (2011).
-
Decelle, A., Krzakala, F., Moore, C. & Zdeborová, L. Asymptotic analysis of the stochastic block model for modular networks and its algorithmic applications. Phys. Rev. E.84, 066106 (2011).
-
Peixoto, T. P. Bayesian Stochastic Blockmodeling. In Advances in Network Clustering and Blockmodeling, 289–332 (John Wiley & Sons, Ltd, 2019).
-
Young, J.-G., St-Onge, G., Desrosiers, P. & Dubé, L. J. Universality of the stochastic block model. Phys. Rev. E.98, 032309 (2018).
-
Newman, M. E. J. Equivalence between modularity optimization and maximum likelihood methods for community detection. Phys.Rev. E.94, 052315 (2016).
-
White, H. C., Boorman, S. A. & Breiger, R. L. Social structure from multiple networks. i. blockmodels of roles and positions. American J. Sociology.81, 730–780 (1976).
-
Price, Dd. S. A general theory of bibliometric and other cumulative advantage processes. J. American Society Inform. Sci.27, 292–306 (1976).
-
Holland, P. W., Laskey, K. B. & Leinhardt, S. Stochastic blockmodels: First steps. Social Networks.5, 109–137 (1983).
-
Nowicki, K. & Snijders, T. A. B. Estimation and Prediction for Stochastic Blockstructures. J. American Statistical Ass.96, 1077–1087 (2001).
-
Girvan, M. & Newman, M. E. J. Community structure in social and biological networks. Proceedings of the National Academy of Sciences99, 7821 –7826 (2002).
-
Schaub, M. T., Delvenne, J.-C., Rosvall, M. & Lambiotte, R. The many facets of community detection in complex networks. Appll. Network sci.2, 4 (2017).
-
Cecchini, G. & Pikovsky, A. et al. Impact of local network characteristics on network reconstruction. Physical Review E.103, 022305 (2021).
-
MacMahon, M. & Garlaschelli, D. Community Detection for Correlation Matrices. Phys. Rev. X.5, 021006 (2015).
-
Masuda, N., Kojaku, S. & Sano, Y. Configuration model for correlation matrices preserving the node strength. Phys. Rev. E.98, 012312 (2018).
-
Medaglia, J. D., Zurn, P., Sinnott-Armstrong, W. & Bassett, D. S. Mind control as a guide for the mind. Nature Human Behaviour.1, 1–8 (2017).
-
Avella-Medina, M., Parise, F., Schaub, M. & Segarra, S. Centrality measures for graphons: Accounting for uncertainty in networks. IEEE Transactions on Network Science and Engineering (2018).
集智斑图顶刊论文速递栏目上线以来,持续收录来自Nature、Science等顶刊的最新论文,追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能,每周通过微信服务号「我的集智」推送论文信息。扫描下方二维码即可一键订阅:




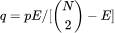 其中N和E是原始网络中的节点和边的数量。以这种方式选择概率 q,使观察到的边的预期数量与原始网络中的相同。人们可能会天真地认为,这种均匀的测量误差的影响仅仅是为原始网络的网络描述符(descriptors)的值引入波动。相反,我们观察到系统性的偏差,将这些值转移到特定的方向,使它们不再与原始网络的值相似,重要的是,它们可以隐藏现有的结构或放大现有的结构。
其中N和E是原始网络中的节点和边的数量。以这种方式选择概率 q,使观察到的边的预期数量与原始网络中的相同。人们可能会天真地认为,这种均匀的测量误差的影响仅仅是为原始网络的网络描述符(descriptors)的值引入波动。相反,我们观察到系统性的偏差,将这些值转移到特定的方向,使它们不再与原始网络的值相似,重要的是,它们可以隐藏现有的结构或放大现有的结构。
 来测量。我们考虑的是以这种有噪声的方式测量出来的网络(“未重构”),以及用参考文献中的贝叶斯方法得到的重构的网络[53]。在进行了 M 个独立的噪声测量后得到的重构网络。我们显示了在每种情况下获得的相应随机行走过渡矩阵的平均局部聚类系数和谱隙的值。误差条对应于后验分布的标准偏差。横线表示原始网络的真实值。
来测量。我们考虑的是以这种有噪声的方式测量出来的网络(“未重构”),以及用参考文献中的贝叶斯方法得到的重构的网络[53]。在进行了 M 个独立的噪声测量后得到的重构网络。我们显示了在每种情况下获得的相应随机行走过渡矩阵的平均局部聚类系数和谱隙的值。误差条对应于后验分布的标准偏差。横线表示原始网络的真实值。