重整化群是普适性和相变理论的基石,是检验动力系统对称性和组织尺度的有力工具。然而,由于不同尺度之间的相关性,它在复杂网络中的应用特别具有挑战性。近日发表于 Nature Physics 的一项研究提出一个基于拉普拉斯重整化群扩散的复杂网络方法,能够在异质网络中识别出合适的时空尺度。
Konstantin Klemm | 作者
郭瑞东 | 译者
朱欣怡 | 审校
邓一雪 | 编辑
Laplacian renormalization group for heterogeneous networks
https://www.nature.com/articles/s41567-022-01866-8
重整化(Renormalization)是一种基于重复粗粒化过程的技术,用于研究统计物理学中的尺度不变性和临界性。最近 Nature Physics 的研究[1],“针对异构网络的拉普拉斯重整化群”,扩展了重整化工具箱,允许探索现实世界网络的尺度不变性。
想象一下从艾菲尔铁塔顶部拍摄一系列照片:塞纳河上的一艘划艇,巴黎圣母院的西立面,继续扩大视野,可以看到整个巴黎的全景。游客在不同的空间尺度上,会看到新鲜且变化的城市印象。另一方面,物理学家最为欣慰的则是,无论尺度放大或缩小,所观察的事物仍然相似。分形结构,如科赫曲线,就具有一种内在的自相似性。
伊辛模型从顺磁到铁磁相变的临界点,可通过粗粒化过程的不变性确定。重整化群是研究物理系统中这种尺度变换效应的一套技术。Pablo Villegas 及其同事的论文 [1],将重整化的范围扩大到超越网格结构的任意网络系统。
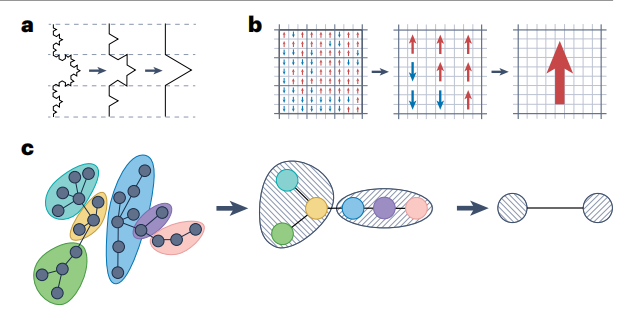
尺度不变性在物理学和数学的不同领域有很多例子。以分形结构为例,它具有内在的自相似性(图1a)。这样的例子还包括伊辛模型在顺磁-铁磁相变的临界点(图1b),这可以通过粗粒化下的不变性来确定(图1b)。由 Leo Kadanoff [2] 提出的 Ising 模型重整化方法是将系统细分为大小相等的块,并将每个子系统的自旋合并为重标度系统的一个块自旋。一旦耦合强度和温度等参数在变换下保持不变,就表明达到了尺度不变性。
Villegas 及其同事扩大了重整化群的应用范围,将其扩展到超越网格结构的任意网络系统。各种生物和技术网络,如生物体的新陈代谢通路及互联网,在适当的块形成方案下具有尺度不变性。然而,并非所有的网络结构都具有这种性质。人工网络,如随机图和随机块模型(stochastic block models)就未能通过尺度不变性测试。
图1.几何和网络系统中的迭代粗粒化。(a)科赫曲线,一个递归构造的分形,通过反转局部构造规则进行粗粒化。(b)正方形网格上的伊辛模型,用 Kadanoff 的块方法进行粗粒化(每个 3×3 块中的上/下自旋被大多数自旋方向所取代)。(c)树状网络(左图)被划分成不同颜色的方块。粗粒度网络(中图)中的超级节点集中了每个区块的节点,该过程通过重复寻找块(条纹气泡)进行粗粒化。这就引出了两节点的网络(右图)。
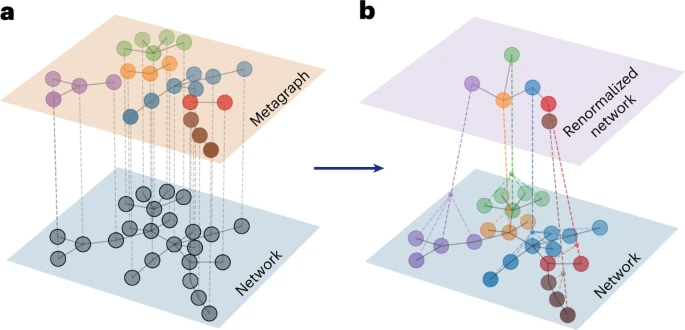
二十多年来,物理学家一直在分析这类真实的网络数据和模型。是什么阻碍了使用现有的重整化技术对网络进行改造?kadanoff 的方法假设了一个基本的几何空间,再把空间分割成块,所有的连边都是短程的,仅连接邻接块中的网格点。但是,网络,纯粹是由边的存在与否定义的。节点不需要附着特定的空间坐标。即使它们有了坐标,连边也不必需是短程的。在人类大脑中,两个神经元之间的间距是微米级的,而轴突(在神经元之间传输脉冲的纤维)的长度可达数厘米。
图2. Kadanoff 方法的示意图。(a)下层为 BA 网络,不同的颜色识别 Kadanoff 超节点。(b)每个块成为单个与原块中每条连边相关联的节点。
这些长程连边的一小部分足以赋予网络小世界属性[3]——在社交网络中被通俗地称为“六度分隔”。任何两个人都由熟人组成的较短的连边被连接起来——如果熟人网络是二维网络,那么距离要比预期短得多。在一个小世界网络中,网络的直径(任意两个节点之间的平均距离)随着节点的数量对数缩放。对任意维度的网格,这可以看作直径标度所具有的无穷维度极限(infinite dimension limit)。因此,大多数真实世界网络表现出的小世界网络特性,实际上描述了有限维度的缺失,从而阻碍了网络在低维欧氏空间中的嵌入。
之前的网络重整化方法[5]尝试通过将网络嵌入到一个二维双曲空间,模拟为庞加莱圆盘(Poincaré disk)解决了这个问题。将所需的块投影到圆盘的边界,呈现为这个一维流形中的簇。这种方法揭示了来源于生物、技术和社会的几个真实网络中明确的尺度不变性。此外,它与来自隐藏度量空间的现有网络理论有着很强的联系。这个研究的不足之处在于,该方法是为可嵌入到双曲几何的网络量身定制的,不适用于其他网络结构,如网格。
Villegas 等人完全摒弃几何学的假设,考虑网络上的扩散过程。他们认为块是扩散过程中具有显著概率流的节点集合(图1c)。概率向量按照热方程(heat equation,即热传导方程)的网络版本演化,由拉普拉斯矩阵(Laplacian Matrix)控制。该矩阵是著名的用于向量计算的拉普拉斯算子的离散对应物。
就像传统的拉普拉斯算子,网络拉普拉斯算子在时间和空间尺度紧密耦合。尤其值得注意的是,网络拉普拉斯算子的特征向量就像在弹性介质中振荡的驻波。波数随着相关特征值变化[6]ーー波越短,振动越快。
Villegas 和同事们利用空间与时间之间的联系,用动量空间方法补充他们的块重整化技术。这里粗粒化投射最大特征值的特征向量,从而消除了网络拉普拉斯算子中的最小空间尺度。此外,粗粒化不仅在空间上展开,而且在时间尺度上展开,使得该方法可以用于动力系统的重整化[7]。
这种基于拉普拉斯算子的粗粒化方法及早期的双曲嵌入法,并不是物理学在网络分割(network partition)方面的首次尝试。更多例子有:基于盒计数(Box-counting)的网络维度估计[8]和社团结构检测[9],这是过去20年开发的一系列分割方法。这些方法大部分是在没有考虑重整化理论的前提下研发的。然而,通过比较新的粗粒化方法和已有的粗粒化方法,可以获得有价值的见解。人们可能希望,基于网络的尺度不变性的鲁棒表征,可以揭示不只一个,而是一组网络分割方案。
但是这一切都是为了什么呢?现实世界网络是有限尺寸的。它们在每个粗粒化步骤中都会收缩,因此重整化总是流向平凡解——单个孤立的节点。那么,我们如何证明网络的尺度不变性呢?一个启发式方法是,通过比较粗粒化前后网络的节点度数分布和其他网络指标来证明。
Villegas 和同事们也发现了扩散过程本身的空间尺度不变性,正如时间无关的熵产生速率所表明的那样。这些研究结果令人兴奋,同时还有一个个基于案例的令人信服的启发式论点。这些发现让我们越来越接近网络尺度不变性这一概念,以及与重整化群取得一致。
本文翻译自:https://www.nature.com/articles/s41567-022-01842-2
原文题目“A zoom lens for networks”。
1. Villegas, P., Gili, T., Caldarelli, G. & Gabrielli, A. Nat. Phys. https://doi.org/10.1038/
s41567-022-01866-8 (2023).
2. Kadanof, L. P. Phys. Phys. Fiz. 2, 263 (1966).
3. Watts, D. J. & Strogatz, S. H. Nature 393, 440 (1998).
4. Eguíluz, V. M., Hernández-García, E., Piro, O. & Klemm, K.
Phys. Rev. E 68, 055102 (2003).
5. García-Pérez, G., Boguñá, M. & Serrano, M. Á. Nat. Phys. 14, 583–589 (2018).
6. Biyikoğu, T., Leydold, J. & Stadler, P. F. Laplacian Eigenvectors of Graphs: Perron–Frobenius and Faber–Krahn Type Theorems (Springer, 2007).
7. Lesne, A. A comparative introduction to the renormalization methods used in statistical mechanics and for dynamical systems. In Workshop on Renormalization in Mathematics and Physics (IHP, 1996); https://www.lptmc.jussieu.fr/user/lesne/rg-IHP-2.pdf
8. Song, C., Havlin, S. & Makse, H. A. Nature 433, 392–395 (2005).
9. Fortunato, S. & Newman, M. E. J. Nat. Phys. 18, 848–850 (2022).