开放的流网络（Open Flow Network），或流动网络，也简称流网络(Flow Network)是指一类特殊的加权有向的复杂网络。其中，有向连边表示能量、物质、货币、信息、注意力等流动的方向，连边的权重则表示流量。开放性体现为网络中存在着源和汇两类特殊的节点代表环境。目前，开放流网络这种模型已经被应用到了生态能量流分析、国际贸易流分析、投入产出关系、大规模的人类行为、集体注意力流等多个学科背景中去了。

南京大学的王成军老师和芝加哥大学的吴令飞博士开发了一个开源工具包Flownetwork，将常用的计算都集成到了一起。初学者可以直接调用该包完成各种有关开放流网络的计算。

该包的主要功能如下：https://github.com/chengjun/flownetwork（或点击阅读原文）

操作演示

首先需要安装flownetwork的包，打开一个终端输入：

pip install flownetwork

然后可以在jupyter notebook（或者其他的地方）中导入安装包：

# import packages  from flownetwork import flownetwork as fn import networkx as nx import matplotlib.pyplot as plt  print(fn.__version__)

然后进行注意力网络的分析：

首先我们可以用help语句来查看一下这个流网络的结构：

help(fn.constructFlowNetwork)

Help on function constructFlowNetwork in module flownetwork.flownetwork: constructFlowNetwork(C)    C is an array of two dimentions, e.g.,    C = np.array([[user1, item1],       [user1, item2],       [user2, item1],       [user2, item3]])    Return a balanced flow networ

在了解了这个网络的架构之后，我们就可以自己创建一个流网络：

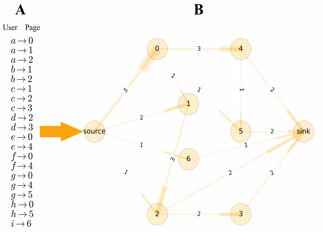
demo = fn.attention_data gd = fn.constructFlowNetwork(demo)

为了更好的了解这个流网络的结构，我们可以利用matplotlib画出这个demo的流网络：

# drawing a demo network fig = plt.figure(figsize=(12, 8),facecolor='white') pos={0: np.array([ 0.2 ,  0.8]),  2: np.array([ 0.2,  0.2]),  1: np.array([ 0.4,  0.6]),  6: np.array([ 0.4,  0.4]),  4: np.array([ 0.7,  0.8]),  5: np.array([ 0.7,  0.5]),  3: np.array([ 0.7,  0.2 ]),  'sink': np.array([ 1,  0.5]), 'source': np.array([ 0,  0.5])} width=[float(d['weight']*1.2) for (u,v,d) in gd.edges(data=True)]  edge_labels=dict([((u,v,),d['weight']) for u,v,d in gd.edges(data=True)])nx.draw_networkx_edge_labels(gd,pos,edge_labels=edge_labels, font_size = 15, alpha = .5)  nx.draw(gd, pos, node_size = 3000, node_color = 'orange',  alpha = 0.2, width = width, edge_color='orange',style='solid') nx.draw_networkx_labels(gd,pos,font_size=18)  plt.show()

然后我们就画出了这个demo的流网络图：

利用下面这条语句，我们查看一下这个demo的一些信息：

nx.info(gd)

如果网络没有达到平衡的话，我们就对网络进行流平衡：

# balancing the network # if it is not balanced  gh = fn.flowBalancing(cd) nx.info(gh)

计算网络的流矩阵，存储在m中：

# flow matrix
m = fn.getFlowMatrix(gd)  m

我们可以看到输出的流矩阵的信息是下面这样子的：

matrix([[ 0.,  1.,  0.,  0.,  3.,  1.,  0.,  0.,  0.],    [ 0.,  0.,  3.,  0.,  0.,  0.,  0.,  0.,  0.],    [ 0.,  0.,  0.,  2.,  0.,  0.,  0.,  0.,  2.],    [ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.,  2.],    [ 0.,  0.,  0.,  0.,  0.,  1.,  0.,  0.,  2.],    [ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.,  2.],    [ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.,  1.],    [ 5.,  2.,  1.,  0.,  0.,  0.,  1.,  0.,  0.],    [ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.]])

计算网络的马尔科夫矩阵：

fn.getMarkovMatrix(m)

我们可以看到输出的马尔科夫矩阵是下列数组的形式：

array([[ 0.,  0.2   ,  0.,  0.,  0.6   ,0.2   ,  0.,  0.,  0.],   [ 0.,  0.,  1.,  0.,  0.,0.,  0.,  0.,  0.],   [ 0.,  0.,  0.,  0.5   ,  0.,0.,  0.,  0.,  0.5   ],   [ 0.,  0.,  0.,  0.,  0.,0.,  0.,  0.,  1.],   [ 0.,  0.,  0.,  0.,  0.,0.33333333,  0.,  0.,  0.66666667],   [ 0.,  0.,  0.,  0.,  0.,0.,  0.,  0.,  1.],   [ 0.,  0.,  0.,  0.,  0.,0.,  0.,  0.,  1.],   [ 0.55555556,  0.22222222,  0.11111111,  0.,  0.,0.,  0.11111111,  0.,  0.],   [ 0.,  0.,  0.,  0.,  0.,0.,  0.,  0.,  0.]])

接着我们计算无穷步长的累积马尔科夫转移矩阵：

fn.getUmatrix(gd)

我们可以看到输出的矩阵是下面这个样子的：

matrix([[ 1.,  0.2   ,  0.2   ,  0.1   ,  0.6   ,0.4   ,  0.], [ 0.,  1.,  1.,  0.5   ,  0.,0.,  0.], [ 0.,  0.,  1.,  0.5   ,  0.,0.,  0.], [ 0.,  0.,  0.,  1.,  0.,0.,  0.], [ 0.,  0.,  0.,  0.,  1.,0.33333333,  0.], [ 0.,  0.,  0.,  0.,  0.,1.,  0.], [ 0.,  0.,  0.,  0.,  0.,0.,  1.]])

最后来统计一下节点的耗散数据：

# return dissipationToSink,totalFlow,flowFromSource fn.networkDissipate(gd)

计算网络中给定节点1的出流和入流：

fn.outflow(gd, 1) fn.inflow(gd, 1)

计算网络中流的平均长度：

fn.averageFlowLength(gd)

计算流网络的平均时间矩阵：

fn.getAverageTimeMatrix(gd)

最后我们进行画图操作：

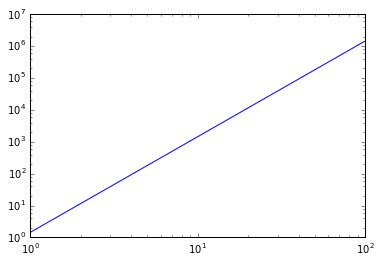
首先将流网络转为树图，然后做出 y = (x+x*[0,1))**3的函数图像(双对数坐标系<log, log>下,近似直线) ：

fig=plt.figure(figsize=(9.9)，facecolor="white" ax=fig.add_subplot(111) fn.plotTree(gd,ax) plt.show()  from random import random x=np.array(range(1,100)) y=(x+random()*x)**3  plt.plot(x,y) plt.xscale('log') plt.yscale("log") plt.show()

这样我们就画出了第一张图：

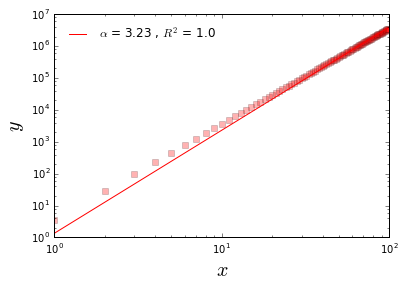
然后我们对: y = (x+x*[0,1))**3的函数图像做最小二乘法线性拟合(双对数条件下,近似直线) ：

fn.alloRegressPlot(x,y,"r","s","$x$","$y$",loglog=True)

画指数截断的幂律分布图：

rg = np.array([ 20.7863444 ,   9.40547933,   8.70934714,   8.62690145,  7.16978087,   7.02575052,   6.45280959,   6.44755478,  5.16630287,   5.16092884,   5.15618737,   5.05610068,  4.87023561,   4.66753197,   4.41807645,   4.2635671 ,  3.54454372,   2.7087178 ,   2.39016885,   1.9483156 ,  1.78393238,   1.75432688,   1.12789787,   1.02098332,  0.92653501,   0.32586582,   0.1514813 ,   0.09722761]) fn.powerLawExponentialCutOffPlot(rg, '$x$', '$p(x)$')

得到如图所示：

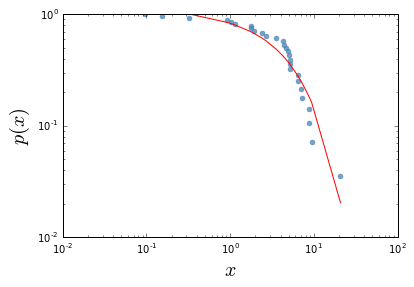
画出DGBD图：

fn.DGBDPlot(rg)  fn.DGBDPlot(rg)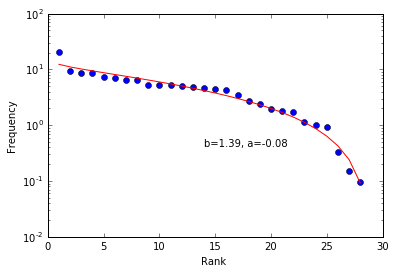

画幂律分布图及拟合曲线：

from networkx.utils import powerlaw_sequence pl_sequence = powerlaw_sequence(1000,exponent=2.5)  fig = plt.figure(figsize=(4, 4),facecolor='white') ax = fig.add_subplot(111) fn.plotPowerlaw(pl_sequence,ax,'r','$x$')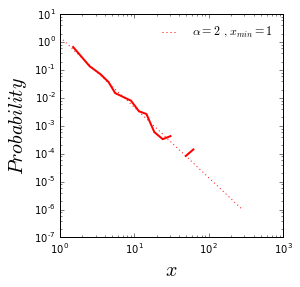

画出CCDF图：

fig = plt.figure(figsize=(4, 4),facecolor='white') ax = fig.add_subplot(111) fn.plotCCDF(pl_sequence,ax,'b','$x$')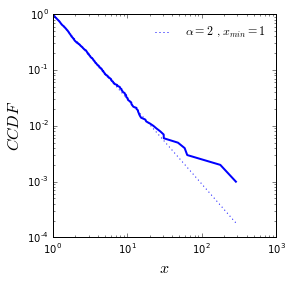

画出基尼系数图：

bins, result, gini_val = fn.gini_coefficient(np.array(pl_sequence))  plt.plot(bins, bins, '--', label="perfect") plt.plot(bins, result, label="observed") plt.title("$GINI: %.4f$" %(gini_val))  plt.legend(loc = 0, frameon = False) plt.show()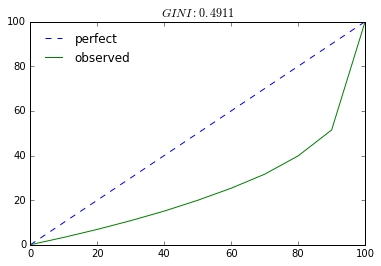

参考资料

http://wiki.swarma.net/index.php/Python 集智wiki上面编写的关于流网络的算法
http://wiki.swarma.net/index.php/%E5%9F%BA%E4%BA%8E%E9%A9%AC%E5%B0%94%E7%A7%91%E5%A4%AB%E9%93%BE%E7%9A%84%E6%B5%81%E7%BD%91%E7%BB%9C%E5%88%86%E6%9E%90 集智wiki上编写的关于基于马尔科夫链的流网络分析