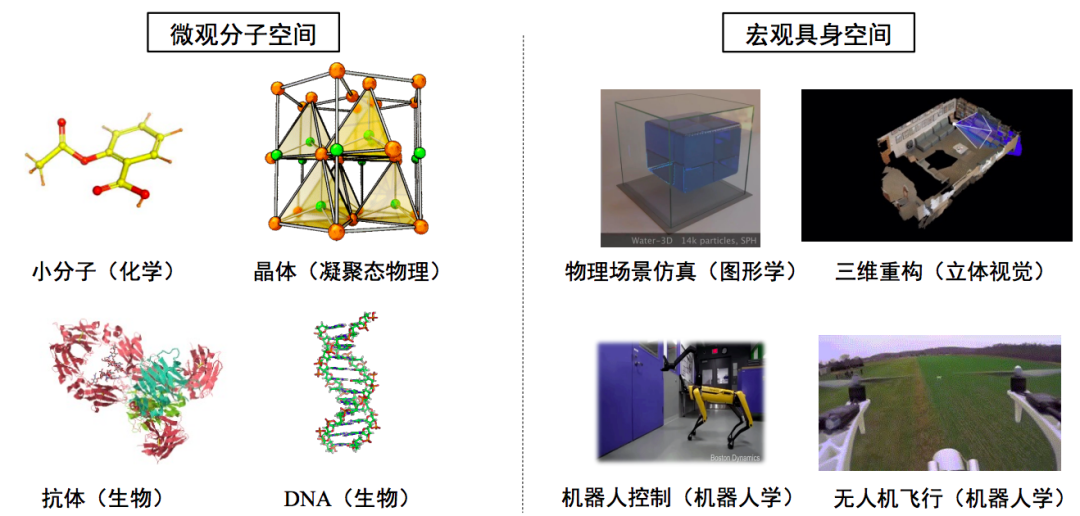
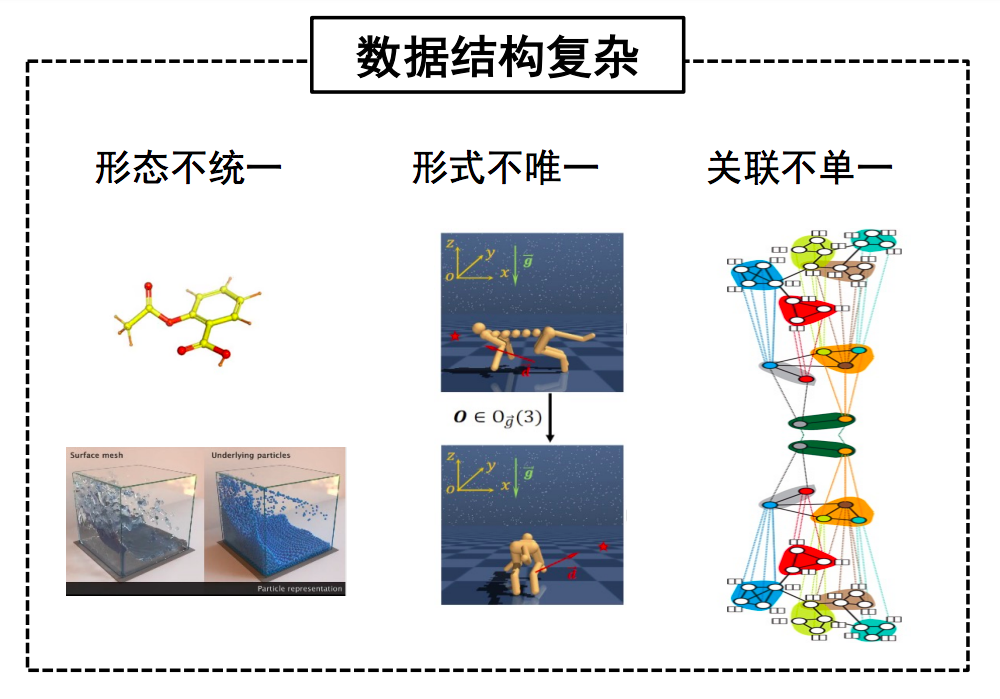
物理空间的数据和任务非常复杂,从微观的分子空间到宏观的具身空间,不仅研究尺度发生巨大变化,数据结构也没有统一的形态、唯一的形式,并且变量间的关联方式也是多样的。如何处理如此复杂多样的数据结构,是一个十分具有挑战的问题。
图1. 从微观分子空间到宏观具身空间,数据结构复杂
几何深度学习旨在寻找一种通用化的数据表示,并以此为基础设计模型,其核心是从对称性或者不变性出发,将几何性质嵌入到机器学习流程当中,更好地刻画数据的内在结构和变化规律,提高算法的表示、泛化、通用能力。
Michael Bronstein 是牛津大学计算机科学教授,几何深度学习(geometric deep learning)概念的提出者。
Michael M. Bronstein, Joan Bruna, Taco Cohen, Petar Veličković. Geometric Deep Learning: Grids, Groups, Graphs, Geodesics, and Gauges, https://arxiv.org/abs/2104.13478
Michael Bronstein et al, Geometric foundations of Deep Learning. https://towardsdatascience.com/geometric-foundations-of-deep-learning-94cdd45b451d
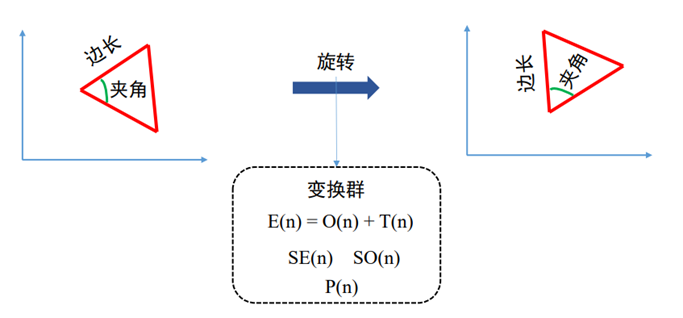
举例来说,下图中左边的三角形经过旋转变换,与右边的三角形是全等的,两者对应的边长和夹角是相等的,这便是欧式空间中的对称性,或者说不变性。
从对称性出发,我们可以对不同的深度学习模型做统一的解释和分类。比如说,CNN具有平移不变性,网络可以对出现在图片中不同位置的同一物体做同样的分类;RNN 具有时移不变性,输入序列整体前移或后移若干 token 并不会影响网络的输出;GNN 则具有顺序不变性,不管一个节点的邻居以怎样的顺序输入网络,经过聚合函数得到的结果都是一样的。
几何深度学习中的一个重要模型是几何图神经网络(Geometric GNN)。
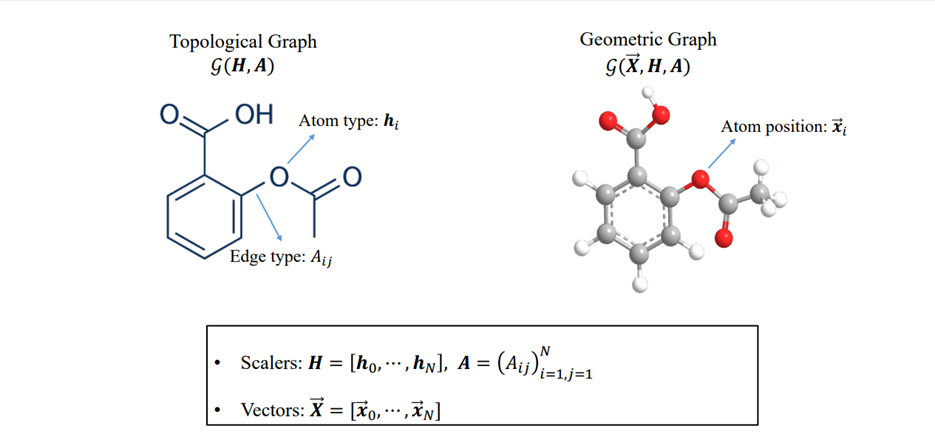
科学领域中的分子、蛋白质、抗体、晶体等物质,以及宏观物理世界中不同形状的物体,均具有特定的空间几何结构,构成了一类重要的数据形态——几何图。与社交网络中的拓扑图不同,几何图中的节点占据一定的空间位置。
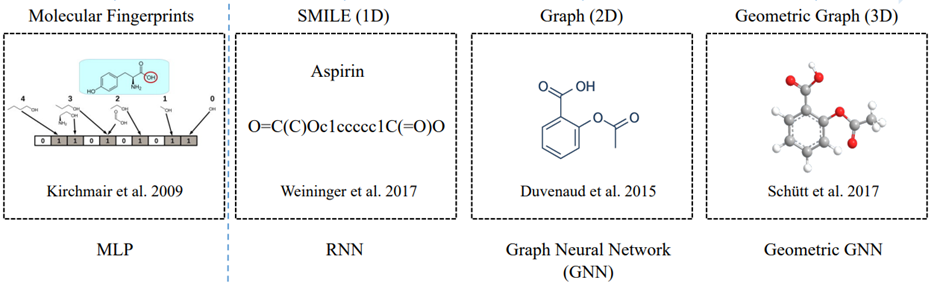
近年来,几何图神经网络由于有效嵌入了对称性,具有良好的解释性、泛化性和通用性,在分子系统表示上得到了广泛应用。以小分子的表示为例,我们可以看到,模型不断发展,可以表征愈加高维的几何性质:
图4:小分子表征模型的发展:多层感知机(MLP),递归神经网络(RNN),图神经网络(GNN),几何图神经网络(Geometric GNN)
最初的 MLP 依赖的是人为提取的特征,即不同的官能团是否存在于分子中(0维);RNN 以分子序列为输入,在一维空间中表征分子序列结构;GNN 则以平面化的分子图为输入,在二维空间中表征分子的拓扑结构。以上几种表征分子的方法都进行了不同程度的简化。而最新的几何图神经网络以分子的几何图为输入,在三维空间中表征分子的空间结构。
下图展示了二维的拓扑图和三维的几何图的区别。除了原子类型和原子键类型之外,几何图还包括了原子的三维坐标,因此也包含了键长键角等信息。
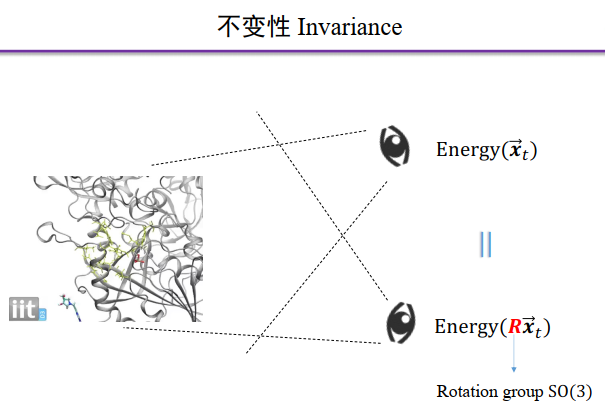
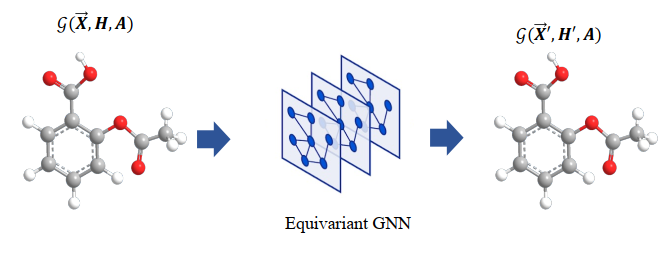
以上是从输入数据的特征对模型做出的区分。此外,我们还可以从对称性出发理解不同的模型。为此我们首先需要了解与对称性有关的两个概念:不变性(Invariance)与等变性(Equivariance)。下图以三维空间里的药物分子为例进行说明。
一种药物的效果通常与它和靶点结合的牢固与否有关,并且可以通过自由能进行判断:自由能越低,结合强度越大。自由能就是一个具有旋转不变性的量:无论我们从何种角度观察这个物理事件,或者如何旋转这个分子以及与它结合的蛋白质,两者结合的自由能都不会改变。用数学语言来说,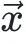 代表关注的物理对象的坐标集合,旋转可以表示为旋转矩阵R,旋转后的坐标为
代表关注的物理对象的坐标集合,旋转可以表示为旋转矩阵R,旋转后的坐标为 ,<求自由能> 表示为函数Energy(),那么
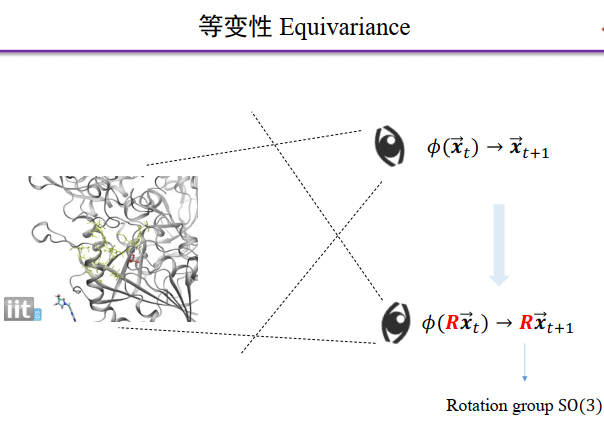
,<求自由能> 表示为函数Energy(),那么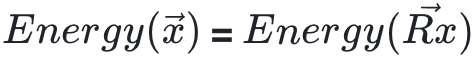 。我们可能也会关心药物分子的运动轨迹:给定t时刻的坐标
。我们可能也会关心药物分子的运动轨迹:给定t时刻的坐标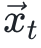 ,我们想用一个函数
,我们想用一个函数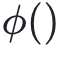 预测下一时刻的坐标
预测下一时刻的坐标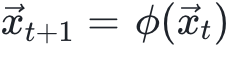 ,那么
,那么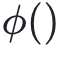 就应该是具有旋转等变性的:经过旋转R,下一时刻的坐标
就应该是具有旋转等变性的:经过旋转R,下一时刻的坐标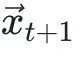 变成了
变成了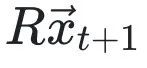 ,
,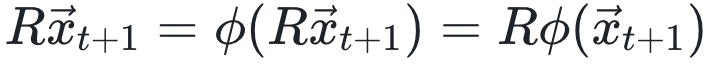 。
。
图6:(左)三维空间中的旋转不变性示意图,(右)三维空间中的旋转等变性示意图
借助等变性和不变性的概念,我们来看看几种不同 GNN 的特点:
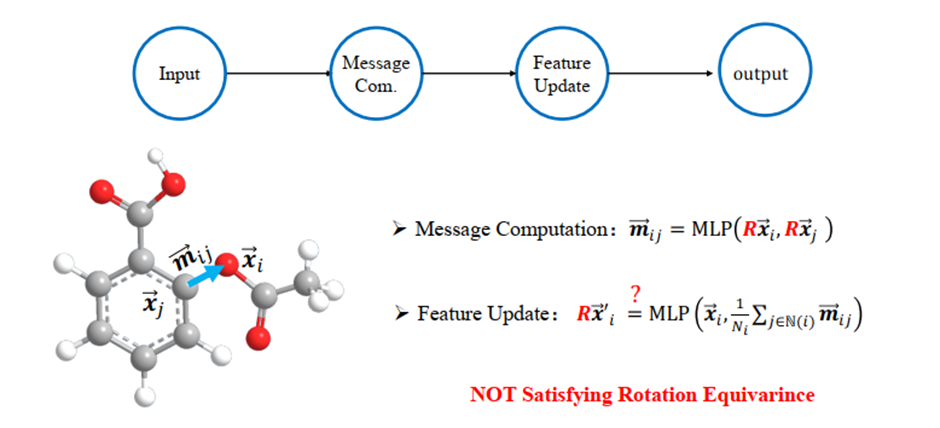
图7:One-layer GNN,不满足旋转等变性
单层的 GNN 通过 message computation(也称message passing)和 feature update 两步操作得到一个输出。其中 message computation 以当前节点和任一邻居节点的特征作为输入,经过一个 MLP,得到该邻居的message;feature update 则是以节点当前特征和不同邻居 message 的聚合为输入,经过另一个 MLP,得到节点更新后的特征。可以看到,由于要经过两个不同的 MLP,其中包含了若干非线性变化,最终网络输出的节点特征更新是不满足旋转不变性或等变性的。
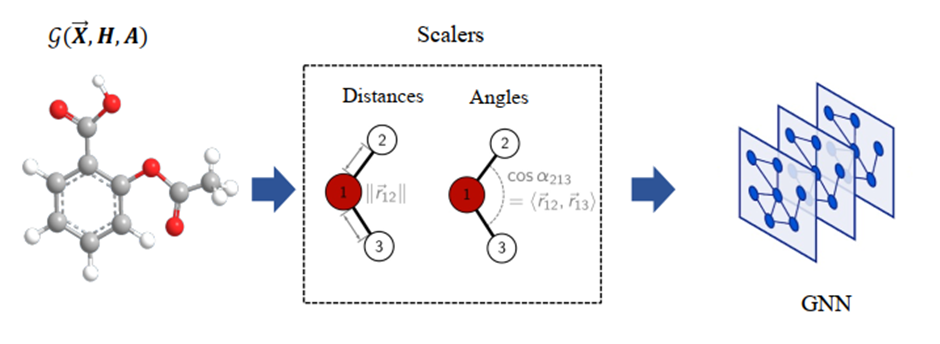
前面我们提到,在欧式空间中,长度和夹角是不会因为旋转而发生变化的。不变GNN就利用了这个几何性质,把原子的坐标替换为了原子键长度和夹角,因此无论怎样变换坐标系,输入是不变的,输出也就是不变的,因此可以用普通的图神经网络进行处理。
但这样的方法也存在一些缺陷,它只能描述局部的几何关系,丢失了全局子图间的相对位置关系。就像毕加索的画作,各五官被打乱又重新组合在脸上,看起来完全失真了。因此该缺陷也被称为毕加索问题(Picasso Problem)。 基于 WL-test 的图同构检测算法无法检测出此类区别,因此辨别能力与 WL-test 相当的GNN结构都会面临同样的问题。
图9:毕加索问题(Picasso Problem),变形的人脸
Johannes Gasteiger, Janek Groß, Stephan Günnemann. Directional Message Passing for Molecular Graphs. ICLR 2020.
简称DimNet,在GNN引入了带方向的消息传播。
Schütt et al. Equivariant message passing for the prediction of tensorial properties and molecular spectra, ICML 2021
Johannes Gasteiger, Florian Becker, Stephan Günnemann. GemNet: Universal Directional Graph Neural Networks for Molecules. NeurIPS 2021.
简称GemNet,一种不变GNN,考虑了球面坐标,效果值得信赖。由DimNet的主要作者打造。
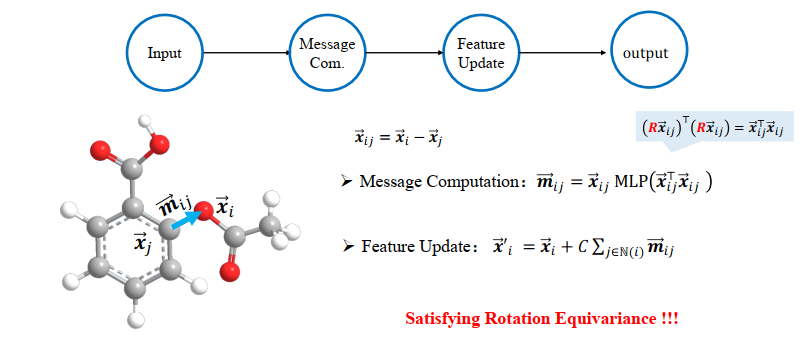
等变 GNN 则在每一层网络中都保留了节点的坐标信息,能很好地解决以上问题。计算每一层的输出时,等变 GNN 也进行了特别设计。首先,用相对坐标代替绝对坐标,满足了平移不变性;其次,在进行 message computation 时,以内积为输入,满足了旋转不变性,于是最终的输出满足了旋转等变性。
Nathaniel Thomas, Tess Smidt, Steven Kearnes, Lusann Yang, Li Li, Kai Kohlhoff, Patrick Riley. Tensor field networks: Rotation- and translation-equivariant neural networks for 3D point clouds. 2018.
这篇论文简称张量场网络TFN,是最早同时满足旋转、平移等变的GNN,在分子动力模拟上进行验证,领域必读文章。
Victor Garcia Satorras, Emiel Hoogeboom, Max Welling. E(n) Equivariant Graph Neural Networks. ICML 2021.
瞩目的 EGNN,目前被广泛使用的等变图神经网络模型,领域必读文章。
Johannes Brandstetter, Rob Hesselink, Elise van der Pol, Erik J Bekkers, Max Welling. Geometric and Physical Quantities Improve E(3) Equivariant Message Passing. ICLR 2022.
简称SEGNN,在EGNN基础上引入了 higer-degree 不可约表示,基于这篇文章可以概括性学习E3不变表示相关知识。
以上思想可拓展到多通道输入的几何特征,得到多通道等变 GNN(GMN)。此外,还有基于球谐函数、基于群论等方式设计的等变GNN,感兴趣的读者可以自行查阅。
Equivariant Graph Mechanics Networks with Constraints, ICLR 2022
Geometrically Equivariant Graph Neural Networks: A Survey. arXiv:2202.07230.
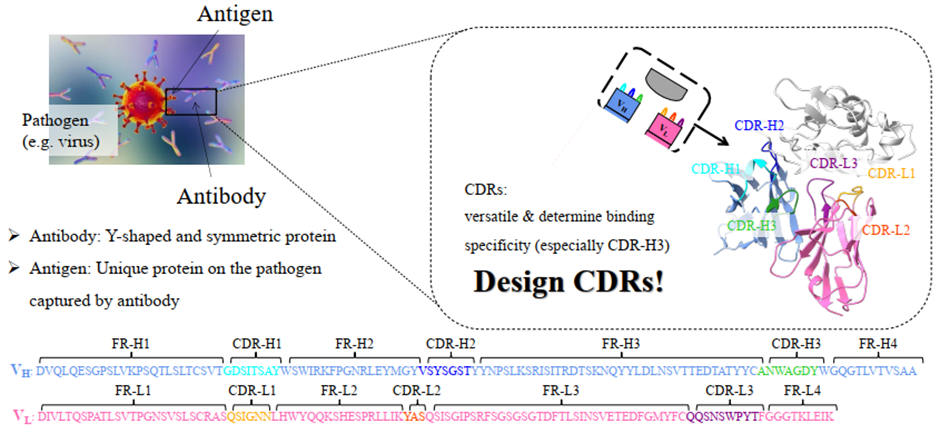
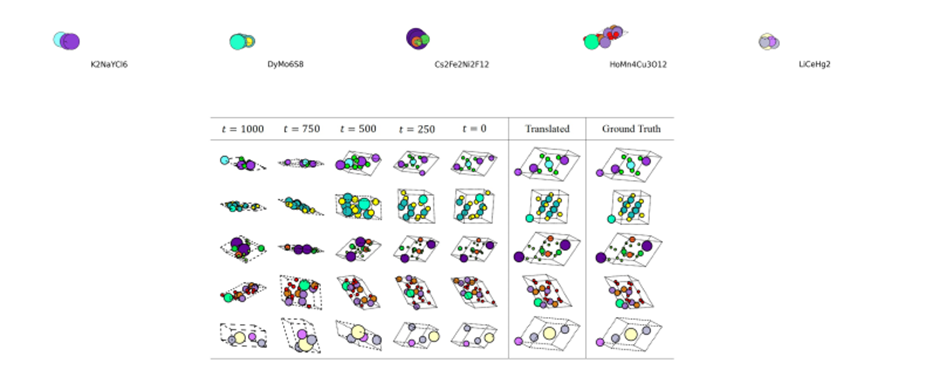
抗体药物与普通小分子药物相比,具有更好的特异性,更少的副作用,也更受青睐。在抗体设计中,我们最关心的是抗体Y字型顶端与抗原结合的可变区域。这些区域实质上是折叠的蛋白质,展开后是氨基酸序列,其中分布着一些相对短的序列,它们表现出极强的多样性,被称为CDRs(complementarity determining regions)。研究证明 CDRs 与抗体特异性识别抗原的能力相关,并且具有高度可变性,因此我们可以人为设计。设计中通常保持其他部分不变,只需要确定构成CDR的氨基酸序列和CDR的三维结构。
Xiangzhe Kong, Wenbing Huang, Yang Liu. Conditional Antibody Design as 3d Equivariant Graph Translation, ICLR 2023 (杰出论文提名)
简称 MEAN,使用等变图神经网络完成抗体 CDR 区域1D氨基酸序列和3D结构的同时生成和优化。
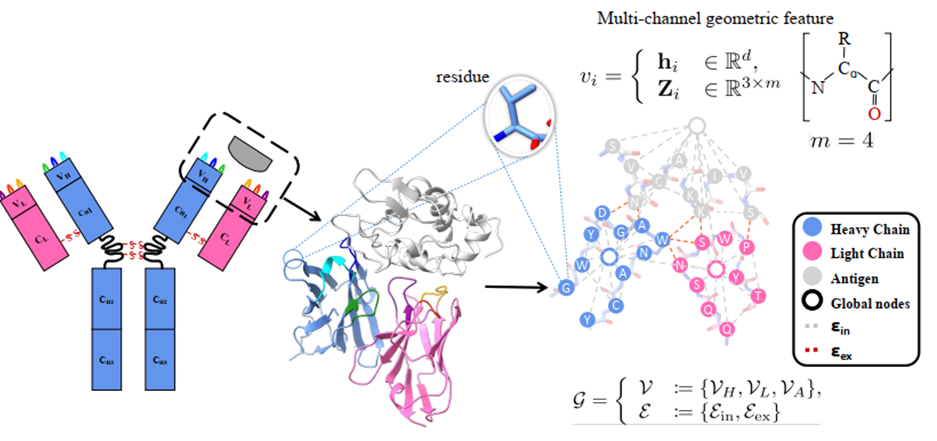
我们现在将抗体设计问题转化为了生成模型设计问题:设计一个生成模型,输入抗原抗体结合部,生成能够与抗原紧密结合的 CDR。自然地,该生成模型应该具有旋转等变性:旋转抗原抗体结合部,生成的 CDR 是经过同样旋转的CDR。多通道等变注意力网络(Multichannel Equivariant Attentive Networks,MEAN)即为这样一种等变 GNN。我们将抗原抗体结合部转化为几何图,每个氨基酸视作一个点,包含两部分(通道)特征,:氨基酸类型特征、:构成氨基酸的基团的坐标;将这些特征输入训练好的多通道等变注意力网络,即可生成相应的 CDRs。
此外,等变图神经网络还可以用于晶体生成和催化剂设计:
晶体的最小重复单元为晶格。晶格是一个包含若干不同种类原子的平行六面体。只需要确定晶格的不同边长及其夹角,以及包含的各原子的坐标,即可以不断重复该晶格而得到晶体。由于晶格具有旋转不变性,因此等变图神经网络也可以用于晶体生成。
Rui Jiao, Wenbing Huang, Peijia Lin, Jiaqi Han, Pin Chen, Yutong Lu, Yang Liu. Crystal Structure Prediction by Joint Equivariant Diffusion on Lattices and Fractional Coordinates. ICLR 2023 Workshop ML4Materials
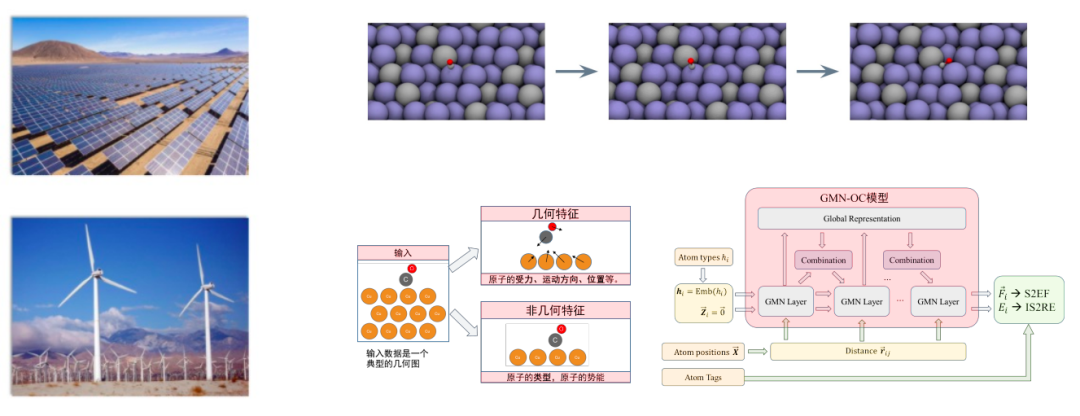
催化剂的催化原理是降低系统发生反应所需要的能量,所以催化剂设计问题可以转化为物理系统能量预测问题,而能量也具有旋转不变性,因此我们可以使用等变图神经网络来预测物理系统能量,而无需再使用密度泛函理论(density functional theory,DFT)求解薛定谔方程。该方法获得了 NeurIPS 2022 Open Catalyst 比赛的冠军。
https://opencatalystproject.org/challenge.html
https://www.youtube.com/watch?v=dFRlpw51Okk
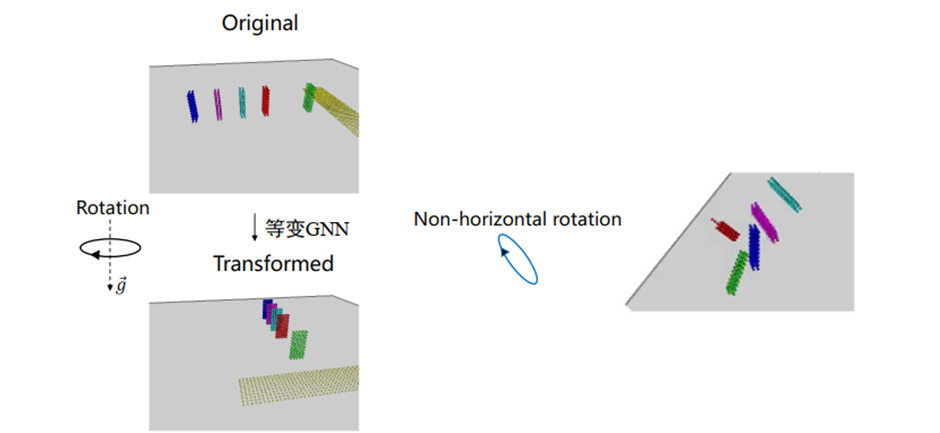
宏观具身空间和微观分子空间最大的区别就是,重力的作用不可忽略,而重力将使得对称性破缺。如果旋转轴平行于重力方向,观测到的物体运动轨迹是旋转等变的;但如果旋转轴与重力方向有夹角,那么物体的运动将不再满足旋转等变性。
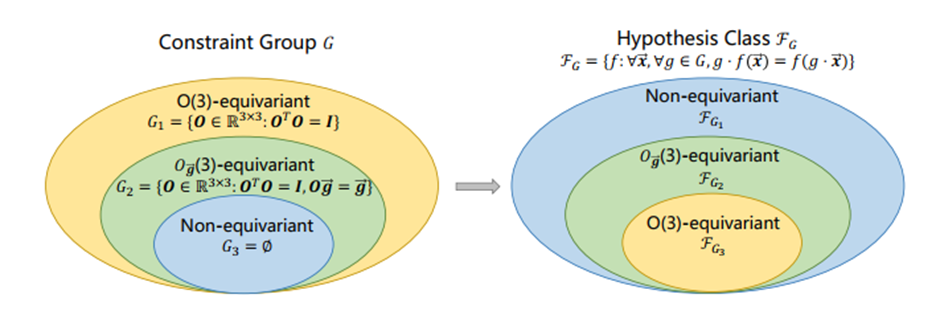
在这样的情况下,我们需要用子等变性描述宏观物理空间的性质,而非前文所提的完全等变性。下图表示了完全等变性(黄色)、重力子等变性(绿色)和非等变性(蓝色)间的关系。从左图,约束(即模型需要满足的性质)来看,子等变性是完全等变性的一个子集;而从右图,约束诱导的模型空间来看,子等变性诱导的模型空间则包含了完全等变性诱导的模型空间,也就是子等变图神经网络(Subequivariant Graph Neural Networks,SGNN)。
Jiaqi Han, Wenbing Huang, Hengbo Ma, Jiachen Li, Josh Tenenbaum, Chuang Gan. Learning Physical Dynamics with Subequivariant Graph Neural Networks, NeurIPS 2022 (Spotlight)
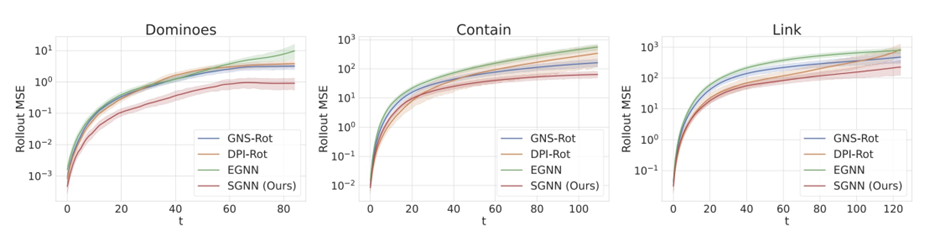
实验结果表明,SGNN 能够比其他类型的图神经网络更真实地模拟物理场景。
图18:物理场景模拟误差,子等变图神经网络(SGNN)vs 其他GNN
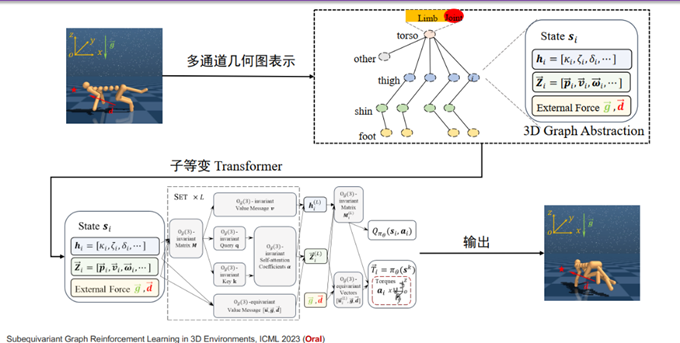
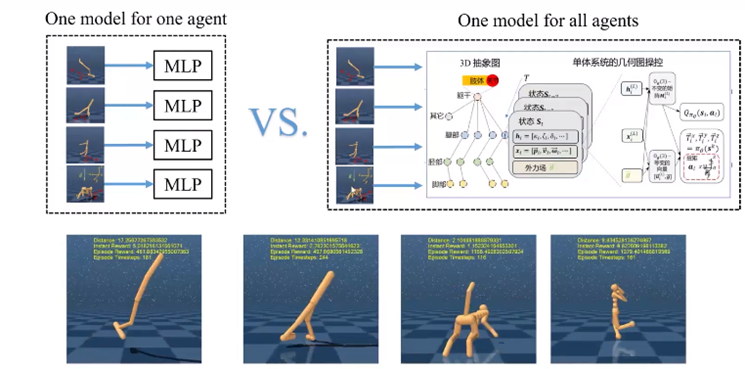
在智能体运动控制上,几何图神经网络也有明显的优势。机器人也可以用图来表示:关节作为点,链接关节的肢体作为边。类似于将分子的表征从2D拓扑图扩展到了3D几何图,几何图神经网络也可以把机器人的建模从2D扩展到3D。再结合重力子等变性,我们就得到了3D子等变强化学习。
Runfa Chen, Jiaqi Han, Fuchun Sun, Wenbing Huang. Subequivariant Graph Reinforcement Learning in 3D Environments, ICML 2023 (Oral)
实验表明,该方法对水平旋转不敏感,能自适应调整方向差异,并且实现了用同一个模型处理不同的智能体。

https://pattern.swarma.org/article/243?from=wechat
黄文炳,中国人民大学高瓴人工智能学院助理教授、博导。曾在清华大学智能产业研究院担任助理研究员,腾讯AI Lab担任高级研究员。研究方向包括几何机器学习理论方法,及其在智能药物发现、物理场景理解与模拟、智能体感知与决策等跨领域任务上的应用。代表性工作包括:训练深度图神经网络的方法 DropEdge;面向大规模图的图神经网络高效训练方法 AS-GCN;针对抗体生成的多通道等变注意力网络 MEAN。
现实世界中大量问题的解决依赖于算法的设计与求解。传统算法由人类专家设计,而随着人工智能技术不断发展,算法自动学习算法的案例日益增多,如以神经网络为代表的的人工智能算法,这是算法神经化求解的缘由。在算法神经化求解方向上,图神经网络是一个强有力的工具,能够充分利用图结构的特性,实现对高复杂度算法的高效近似求解。基于图神经网络的复杂系统优化与控制将会是大模型热潮之后新的未来方向。
为了探讨图神经网络在算法神经化求解的发展与现实应用,集智俱乐部联合国防科技大学系统工程学院副教授范长俊、中国人民大学高瓴人工智能学院助理教授黄文炳,共同发起「图神经网络与组合优化」读书会。读书会将聚焦于图神经网络与算法神经化求解的相关领域,包括神经算法推理、组合优化问题求解、几何图神经网络,以及算法神经化求解在 AI for Science 中的应用等方面,希望为参与者提供一个学术交流平台,激发参与者的学术兴趣,进一步推动相关领域的研究和应用发展。读书会从2023年6月14日开始,每周三晚 19:00-21:00 举行,持续时间预计8周。欢迎感兴趣的朋友报名参与!




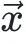 代表关注的物理对象的坐标集合,旋转可以表示为旋转矩阵R,旋转后的坐标为
代表关注的物理对象的坐标集合,旋转可以表示为旋转矩阵R,旋转后的坐标为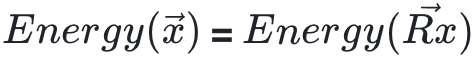 。我们可能也会关心药物分子的运动轨迹:给定t时刻的坐标
。我们可能也会关心药物分子的运动轨迹:给定t时刻的坐标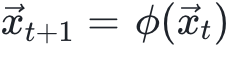 ,那么
,那么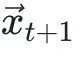 变成了
变成了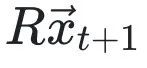 ,
,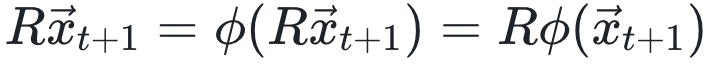 。
。