前沿速递:超越幂律度分布的无标度网络

关键词:复杂网络,无标度性,幂律分布,网络连通性度量


论文题目: Scale-free networks beyond power-law degree distribution 论文地址:https://www.sciencedirect.com/science/article/abs/pii/S0960077923010755?dgcid=authorBook
复杂网络在各个领域中通常被认为是无标度的,这是一种统计特性,通常仅由节点度数 k 的幂律分布来表征。然而,这种表征是不完备的。在真实世界网络中,度与度之间的距离(degree–degree distance) η 的分布是一种类似于 k 的简单基于链接的网络连通性度量,它似乎表现出比 k 更强的幂律分布。虽然 η 的发现提供了无标度性的另一种表征,但却引发了一个根本性问题:k 和 η 的幂律是否代表相同的无标度性?
为了回答这个问题,本文研究了 k 和 η 分布之间的精确渐近关系,证明每个具有 k 幂律分布的网络也具有 η 幂律分布,但反之则不然。这促使研究者引入两个网络模型作为反例,它们具有 η 幂律分布但没有 k 幂律分布,分别使用偏好依附和适应性机制构建。当模拟真实世界网络时,这两个模型每个只需要拟合一个模型参数就可以显示出良好的准确性。这些研究结果表明,η 是无标度性更合适的指标,并可以更深入地理解无标度网络的普适性和基本机制。
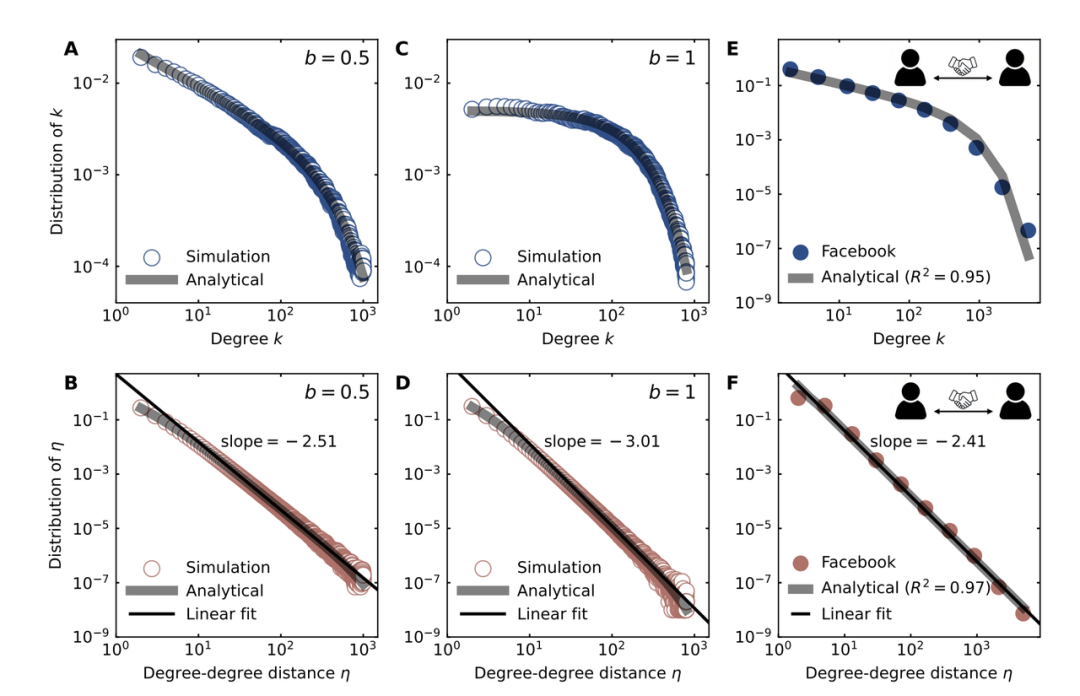

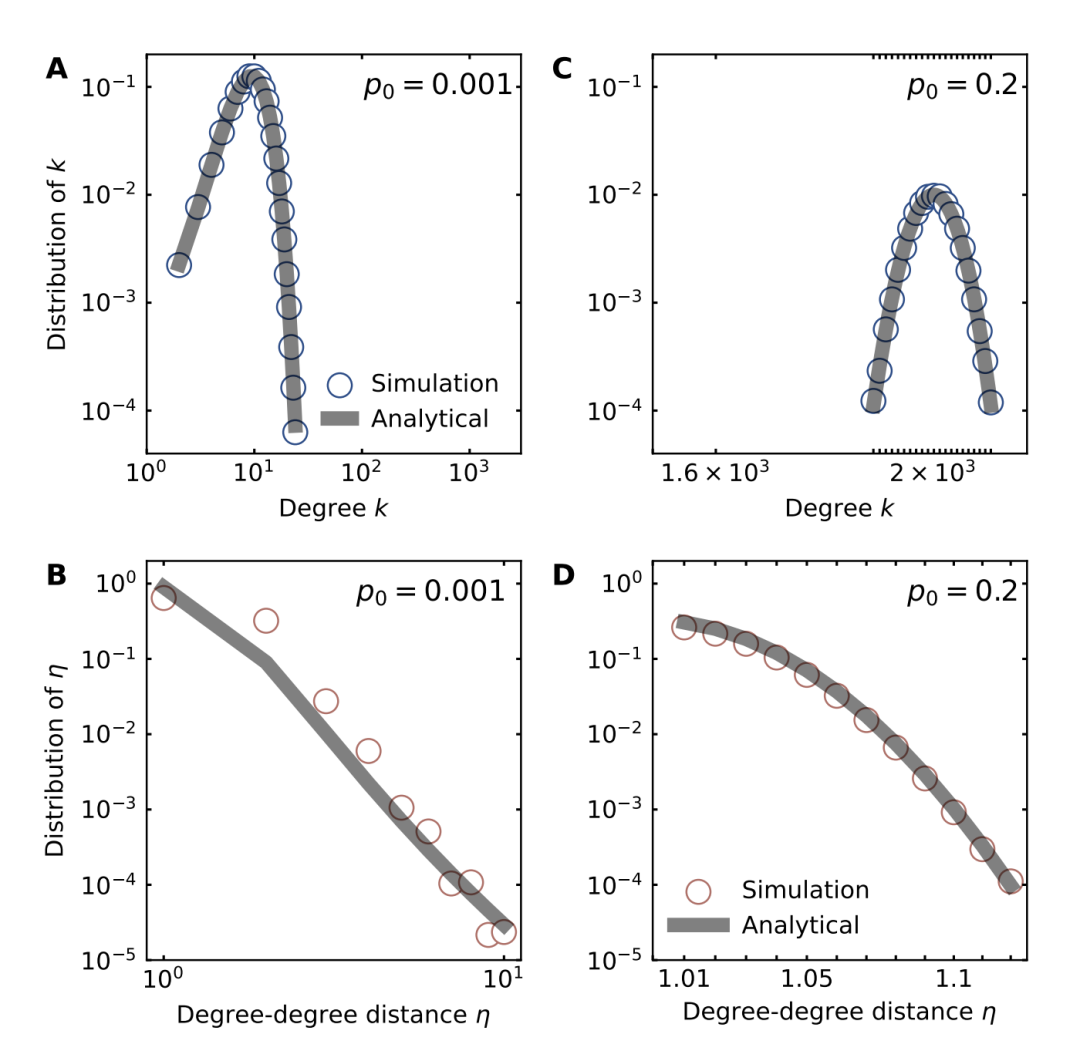
图3. 连接概率固定的 Erdos– Rényi 网络的 k 和 η 分布。
复杂科学最新论文

推荐阅读










