如何从一个复杂系统的原始数据中发现错综复杂的因果结构并识别因果涌现?如何利用因果机制推断系统未来的状态和演化?机器学习、互信息分解、因果推断等新兴技术将为我们提供新的解决方案。由北京师范大学系统科学学院张江教授、清华大学计算机科学学院崔鹏副教授,以及瑞典卡罗琳斯卡医学院高级研究员 Hector Zenil 合作在 Entropy 杂志发起的 Causality and Complex Systems 特刊正在征稿中,集智俱乐部因果涌现社区成员对特刊中的已发表的论文做了简单介绍,欢迎对相关话题感兴趣的研究者投稿。
研究领域:复杂系统,因果涌现,因果科学,机器学习,信息论
复杂系统无处不在。系统复杂性的一个原因是,大型系统中不同层次上广泛存在纠缠的因果结构。在复杂系统中,因果关系可能是涌现的,这意味着如果对系统进行适当的粗粒化操作,那么更强的因果关系可能只在宏观层面而不是微观层面观察得到。更进一步,自上而下的因果关系,即系统中的宏观状态变量影响微观状态变量,也可以在活系统或社会系统中观察到。
然而,我们如何从一个复杂系统的原始数据中发现这些错综复杂的因果结构并识别因果涌现,以及如何利用这些因果机制推断系统未来的状态和演化,这些都是重要而又困难的问题。机器学习、互信息分解、因果推断等新兴技术将为我们提供新的解决方案。
在本期特刊中,我们将重点关注但不限于以下主题:
因果发现(Causal discovery)
因果推断(Causal inference)
因果涌现(Causal emergence)
自上而下因果(Downward causality)
因果的信息论测量(Information theoretic measure of causality)
信息分解(Information decomposition)
因果表征学习(Causal representation learning)
基于因果的机器学习(Machine learning based on causality)
基于机器学习的重整化(Renormalization based on machine learning)
Entropy 杂志 Causality and Complex Systems 特刊目前仍在征稿中,欢迎对相关话题感兴趣的研究者投稿,会议文章也可投稿。
期刊:Entropy (ISSN 1099-4300)
主题:因果与复杂系统(Causality and Complex Systems)
https://www.mdpi.com/journal/entropy/special_issues/causality_complex_systems
目录
1. 生物与技术中的动力因、形式因、质料因和目的因
2. 线性动力系统因果估计的自助抽样法比较综述
3. 因果涌现中的神经信息挤压器
4. 闪烁涌现:涌现的信息论方法中的局部性问题
5. 信息几何进行因果性分析的比较
6. 使用收敛交叉映射推断环境因素与呼吸道感染之间的因果关系
7. 基于核格兰杰因果性的精神分裂症 MEG 网络分析
1. 生物与技术中的
动力因、形式因、质料因和目的因
论文题目:Efficient, Formal, Material, and Final Causes in Biology and Technology
论文地址:https://www.mdpi.com/1099-4300/25/9/1301
作者:George F R Ellis,开普敦大学数学
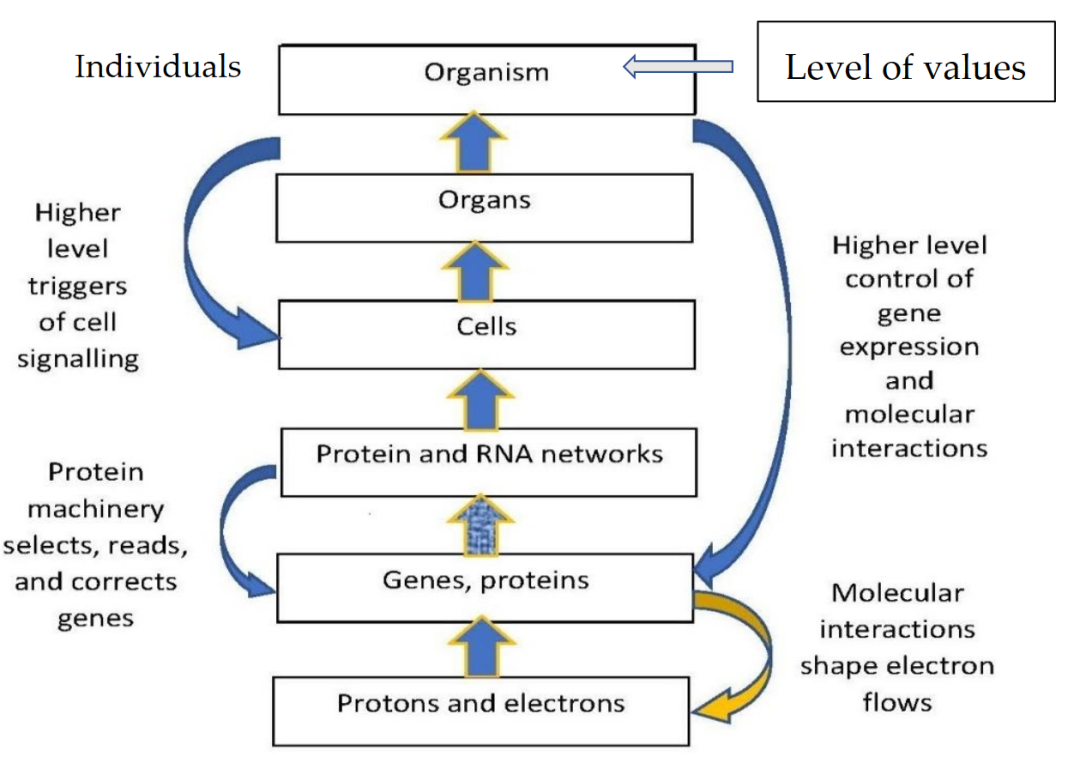
像生命体这样一个复杂系统,往往有多个层级,比如最底层是原子和电子,再往上是基因和蛋白质、RNA网络、细胞、器官一直到整个有机体。一方面还原论告诉我们,任何现象可以还原到它的一部分进行因果地解释,比如细胞间的行为可以追溯到原子的变化,可另一方面我们又认为基因与细胞都应该具有独立的因果能力,两者产生了矛盾。对此,作者提出每个层级都有各自真正的因果关系,并定义有效因果:系统S在某层级L上,有法则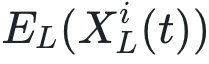 ,能够在给定初值
,能够在给定初值 的条件下确定未来每个时刻的值
的条件下确定未来每个时刻的值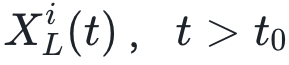 。
图1. 生命体复杂系统的层级结构,自上而下与自下而上的相互作用发生互动
进一步,这种有效因果关系来自向上和向下因果作用的组合,比如某些细胞的死亡导致脑卒中,进而导致某一部分脑组织细胞的死亡。作者基于亚里士多德的四因说(形式因、质料因、动力因和目的因),在大量例子中阐释不同类型的因果作用,论证多个层级上的涌现是真实的,无法在某个底层的物理层级上解释所有的现象。
。
图1. 生命体复杂系统的层级结构,自上而下与自下而上的相互作用发生互动
进一步,这种有效因果关系来自向上和向下因果作用的组合,比如某些细胞的死亡导致脑卒中,进而导致某一部分脑组织细胞的死亡。作者基于亚里士多德的四因说(形式因、质料因、动力因和目的因),在大量例子中阐释不同类型的因果作用,论证多个层级上的涌现是真实的,无法在某个底层的物理层级上解释所有的现象。
论文题目:Comparison of Bootstrap Methods for Estimating Causality in Linear Dynamic Systems: A Review
论文地址:https://www.mdpi.com/1099-4300/25/7/1070
作者:Fumikazu Miwakeichi, Andreas Galka,日本统计数学研究所,德国基尔大学
这项研究中,作者对四种不同的自助抽样法(Bootstrap Method)在时间序列数据中评估因果分析显著性的性能进行了全面比较。为此通过线性反馈系统产生了多变量的模拟数据。这里调查的方法包括无相关相位随机化 Bootstrap(uPRB),它通过在频域随机化相位来生成无交叉相关变量的替代数据;时间偏移 Bootstrap(TSB),它通过在时间域随机化相位来生成替代数据;平稳 Bootstrap(SB),它计算弱相关平稳观测的标准误差并构建置信区间;以及AR-Sieve Bootstrap(ARSB),一种基于自回归(AR)模型的重采样方法,用于逼近底层数据生成过程。
uPRB 方法可以准确识别变量之间的相互作用,但在某些变量中无法检测到自反馈。尽管TSB方法效果不如uPRB,但它也无法检测到某些变量之间的反馈。SB方法给出了一致的因果结果,尽管随着均值分块宽度的增加,它检测自反馈的能力会减弱。ARSB方法表现出优越的性能,在所有变量中准确检测到自反馈和因果关系。关于冲击响应函数(IRF)的分析,只有ARSB方法能够在所有变量中准确检测到自反馈和因果关系,并与连接图相吻合。其他方法在检测性能方面存在显著的变化,有些检测到了误报,而其他仅能检测到自反馈。
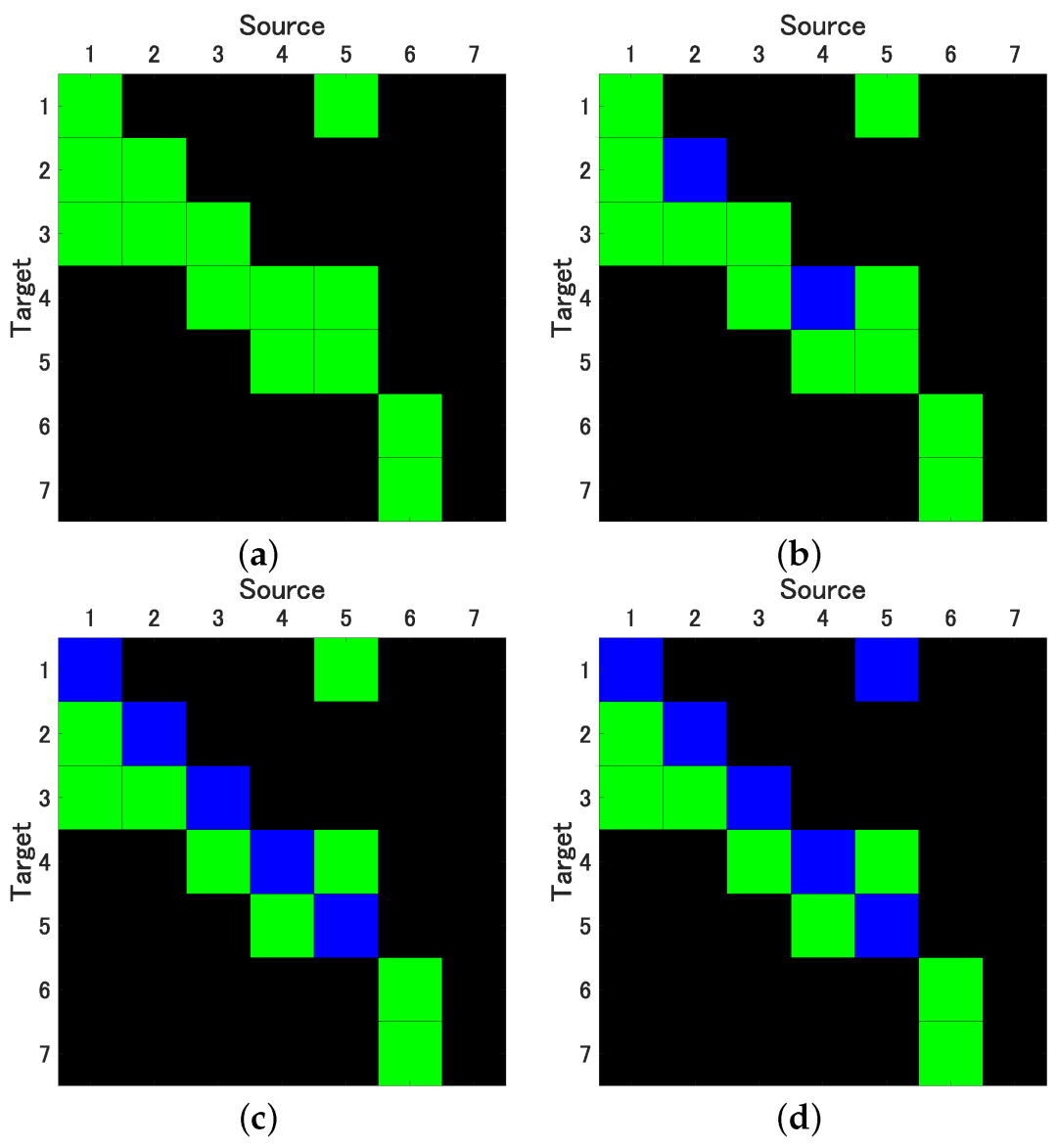
图1.(a)用平均块宽度 w = 5 的相关平稳 Bootstrap (cSB)评价 Granger 因果关系的结果; (b) 平均块宽度 w = 10 和(c) w = 40 的不相关平稳 Bootstrap (ucSB); (d) 时间移位自助法
对于SB方法,研究中确定了最佳平均块宽度w,选择5、10、20和40的值。如图1a所示,无论选择的平均块宽度如何,cSB方法始终产生正确的因果关系结果。相比之下,ucSB方法在 w = 5 时产生了正确的因果关系结果,但自反馈的检出率随着w的增加而降低(见图1b,c)。
图2. 显著性 IRFlms 的二维表示。a显示了每个变量(m = 1, …, 7)分配的影响的 IRFs,ucARSB评估其显著性。cSB方法对于前五个变量的结果几乎与ARSB方法完全相同。然而,它检测到了从第六个到第七个变量的响应,构成了一个错误的正检,这在均值块宽度的所有测试值中都观察到。uPRB方法主要检测到直接耦合变量之间的因果关系(c)。此外,还出现了假阳性,例如第一个和第七个变量之间的互相响应以及第五个和第六个变量之间的互相响应。在评估的自助法中,无论测试的均值块宽度如何,ucSB方法都展现出最弱的检测性能,仅检测到自反馈(d)。
论文题目:Neural Information Squeezer for Causal Emergence
论文链接:https://www.mdpi.com/1099-4300/25/1/26
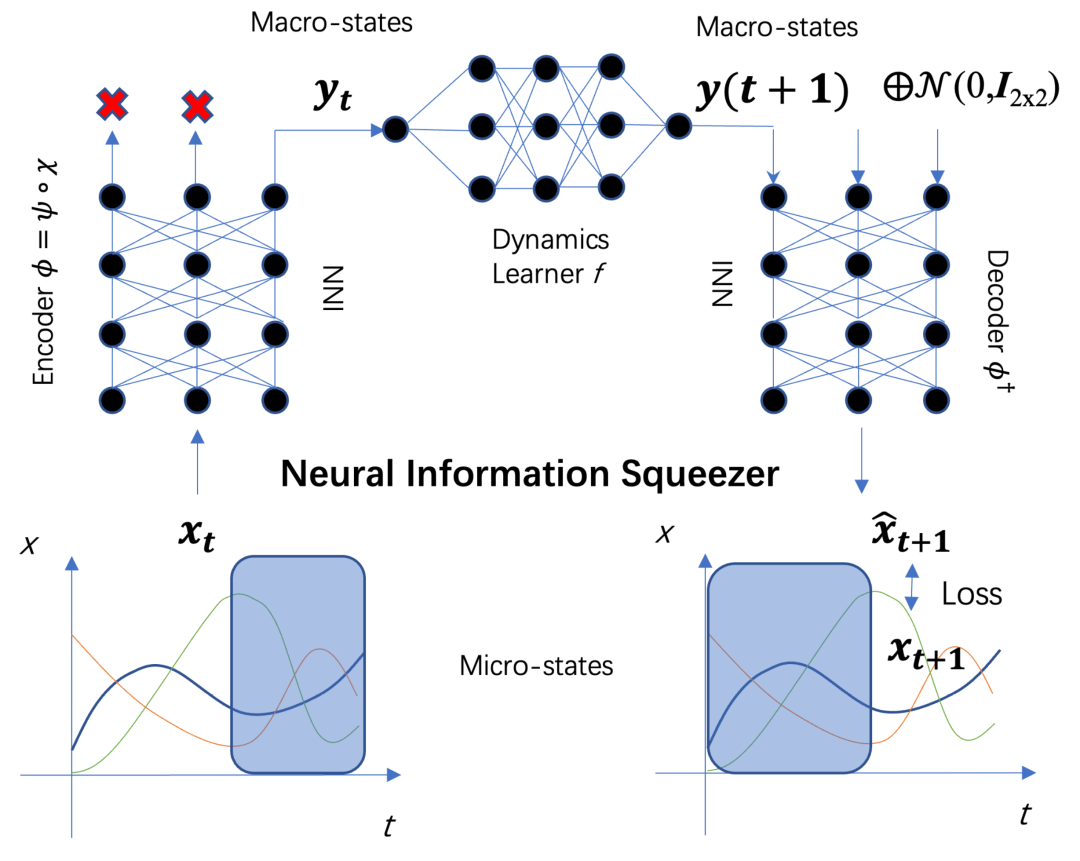
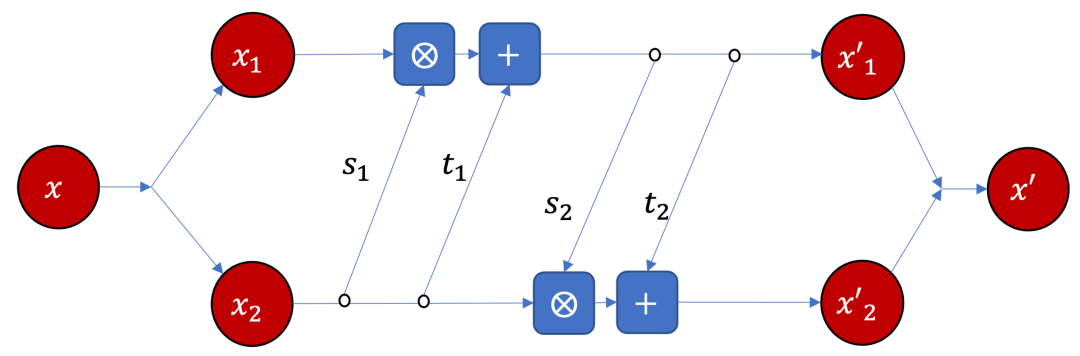
通过神经网络,我们可以对一些动力学模型进行相应的预测。在先前的研究中,我们将因果涌现识别问题表述为在微观动力学精确预测的约束下,宏观动力学的有效信息(effective information,EI)的最大化问题。本文提出一个通用的机器学习框架,称为神经信息挤压器(Neural Information Squeezer, NIS)来解决这个问题。通过使用可逆神经网络对粗粒度策略进行建模,我们可以将从高维到低维的任何映射分解为一系列信息转换、可逆过程和信息丢弃过程。这样,该框架不仅可以以精确的方式控制信息的转换和丢弃,还可以从理论上对整个框架进行数学分析。
NIS由三个组件组成:编码器、动力学学习器和解码器。编码器将微观状态映射到宏观状态 ,这种映射可以分为两个步骤。第一步是双射(可逆)映射,不丢失信息,并由可逆神经网络实现,第二步是通过丢弃p维上的信息,将p维向量投影到q维,p>q。可逆网络可以用RealVnp网络实现。
在模块中,输入向量可以分为两部分,两个向量将被缩放、平移和再次合并。解码器将下一时间步长的预测的宏状态转换为下一时间步骤的微观状态的预测。通过学习系统动力学,得到映射方程,动力学学习器是一个常见的参数为 𝛽的前馈神经网络,它将在宏观层面上学习有效的马尔可夫动力学。随后我们可以通过学习到的模型,进行有效信息EI的预测,从而计算从p维到q维的约减中,是否产生因果涌现。
论文题目:Flickering Emergences: The Question of Locality in Information-Theoretic Approaches to Emergence
论文地址:https://www.mdpi.com/1099-4300/25/1/54
作者:Thomas F Varley,印第安纳大学生理与脑科学系
目前在量化涌现领域,有两个主流的量化框架,分别是 Hoel 提出的因果涌现框架和 Rosas 提出的信息分解计算。在对系统多尺度建模下,使用信息论的工具分析和计算微观态与宏观态的信息传递。这两个框架有一个共同特点,均会计算出一个特定的指标,根据该指标值的大小来识别是否有涌现发生。比如 Hoel 认为,如果宏观的有效信息(effective information)比微观的有效信息更大,则发生涌现。而在信息分解框架下,如果协同信息计算出大于0,则认为发生涌现。但整体上被判断出发生涌现的系统不一定每个部分或状态上都是涌现的。比如一个鸟群因为捕食者或其它因素暂时被冲散开,此时它并没有我们所关心的涌现现象,但不会被有效信息或协同信息反映出来。所以我们能否给出一个系统发生涌现时更精细的结构?
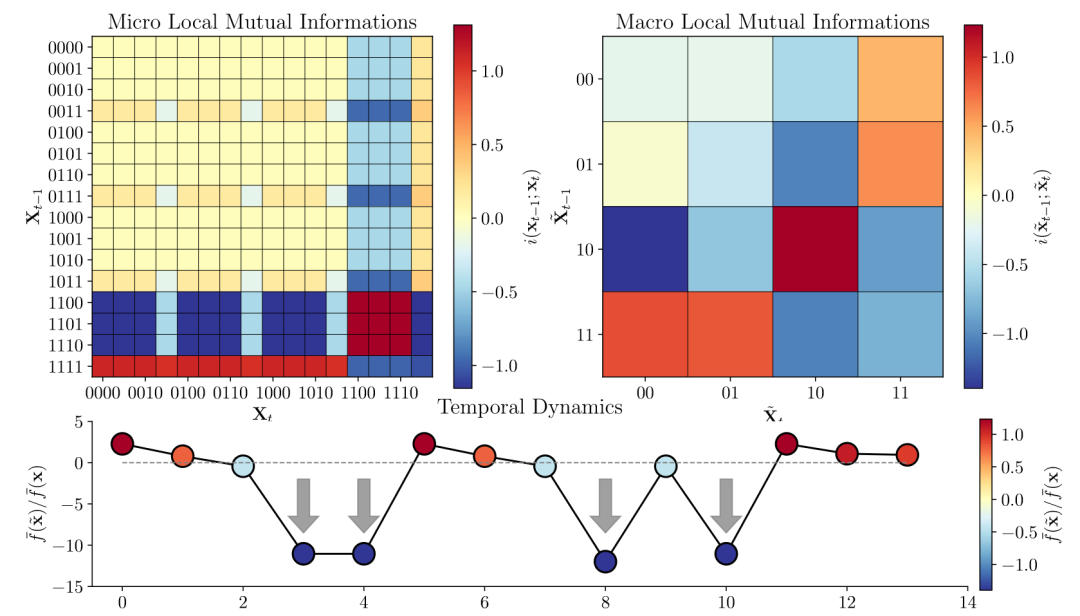
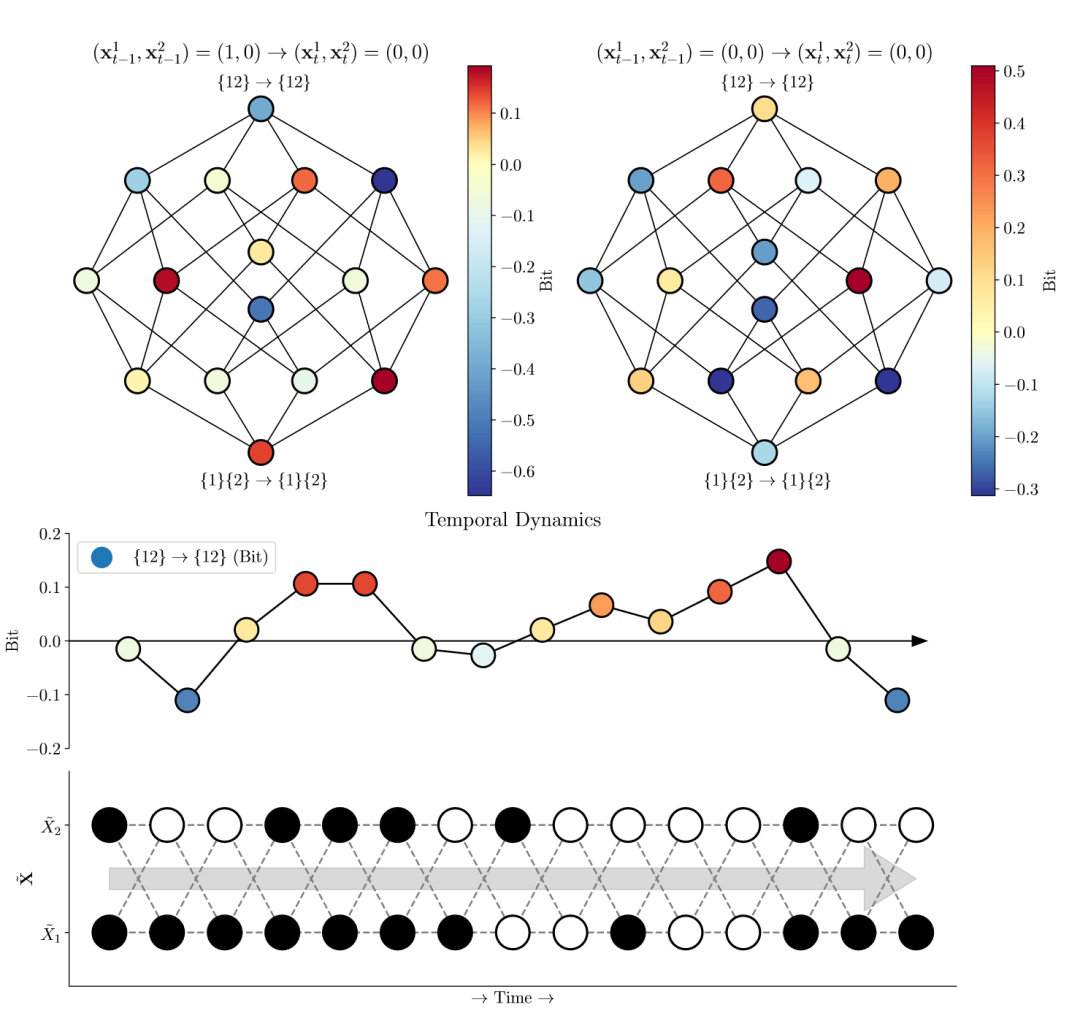
作者基于局部信息论的理论,分别对两个框架进行扩展,得到局部有效信息和局部高阶关系。如果我们发现所有的局部没有表现的非常一致,也就是说,我们更应该把它看成一系列局部的集合而不是一个整体的时候,称这种现象为闪烁涌现(flickering emergence)。在具体计算上,只需要把过剩熵(excess entropy)的计算里互信息替换为局部互信息。局部互信息的期望即为整体的互信息。在这种拓展的视角下,作者重新计算以前的经典案例,发现闪烁涌现的现象非常普遍。
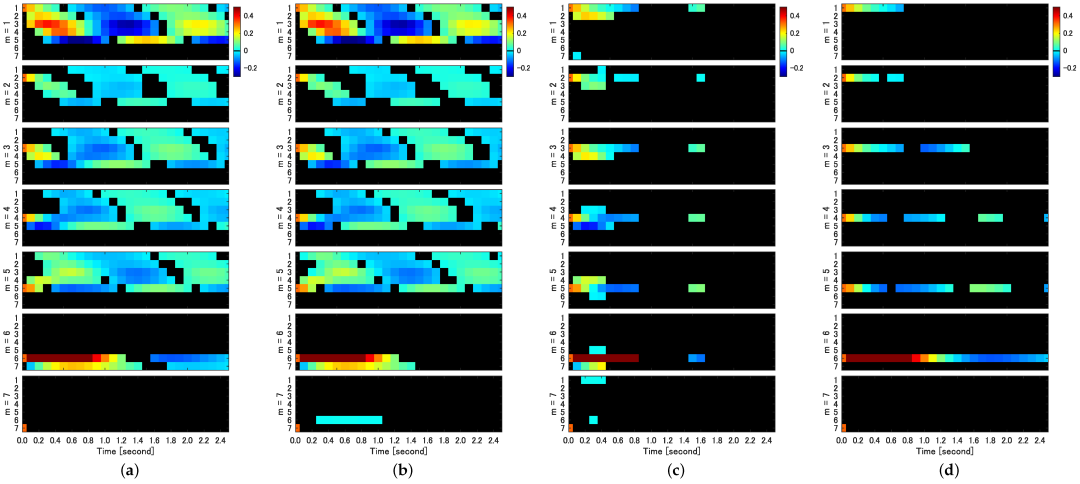
图1. 上:微观和宏观马尔科夫转移矩阵的局部有效信息的分布。每一对事件之间的转移都对应一个局部有效信息的值。下:考虑微观马尔科夫矩阵上的一个随机游走,每一时刻可以得到微观(分母)和宏观(分子)上的局部有效信息。箭头所指为微观局部有效信息为正,而宏观局部有效信息为负,说明在这些地方粗粒化是糟糕的。
图2. 上:信息分解的晶格图,其中每一个结点(表示宏微观变量各分量之间的信息传递)都被计算。中:随着时间变化,宏观变量之间与微观变量独立的信息传递大小的变化。其中小于0的部分表示宏观变量传递了误导信息。下:展示了观测数据,即一个二维变量的时间序列。
论文题目:Causality Analysis with Information Geometry: A Comparison
论文地址:https://www.mdpi.com/1099-4300/25/5/806
作者:Heng Jie Choong, Eun-jin Kim, Fei He,英国考文垂大学
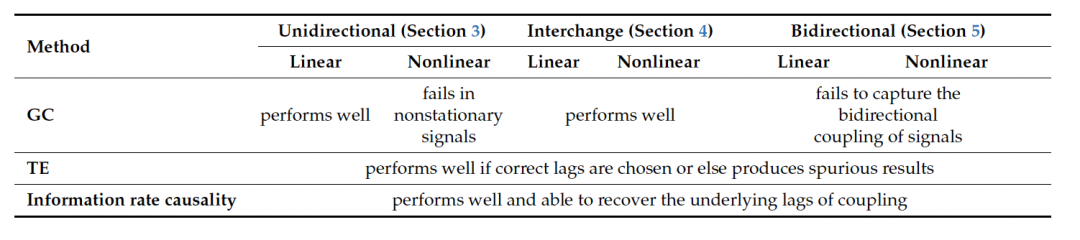
目前在用于量化因果关系的各种分析方法中,最广泛使用的方法是:格兰杰因果性(Granger causality,GC)和转移熵(Transfer Entropy,TE),这两种方法都依赖于根据较早时间另一个过程的知识来提高对一个过程的预测。尽管有相同的概念,它们用于量化因果关系的方法完全不同。GC基于通过比较在建模信号时加入随机过程 x1(t) 信息来预测 x2(t) 信息和仅使用 x2(t) 本身信息的线形自回归模型的误差来进行定量研究,但线性模型不能适应现实世界信号内可能存在的非线性和非平稳效应。另一方面,TE是一种无模型方法,采用了统计依赖性方法来访问因果性。虽然TE不受任何特定模型或线性假设的限制,但对于高斯过程,它可以产生与GC类似的结果。因此,这两种方法在应用于非线性、非平稳数据或非参数模型时都各自存在局限性。
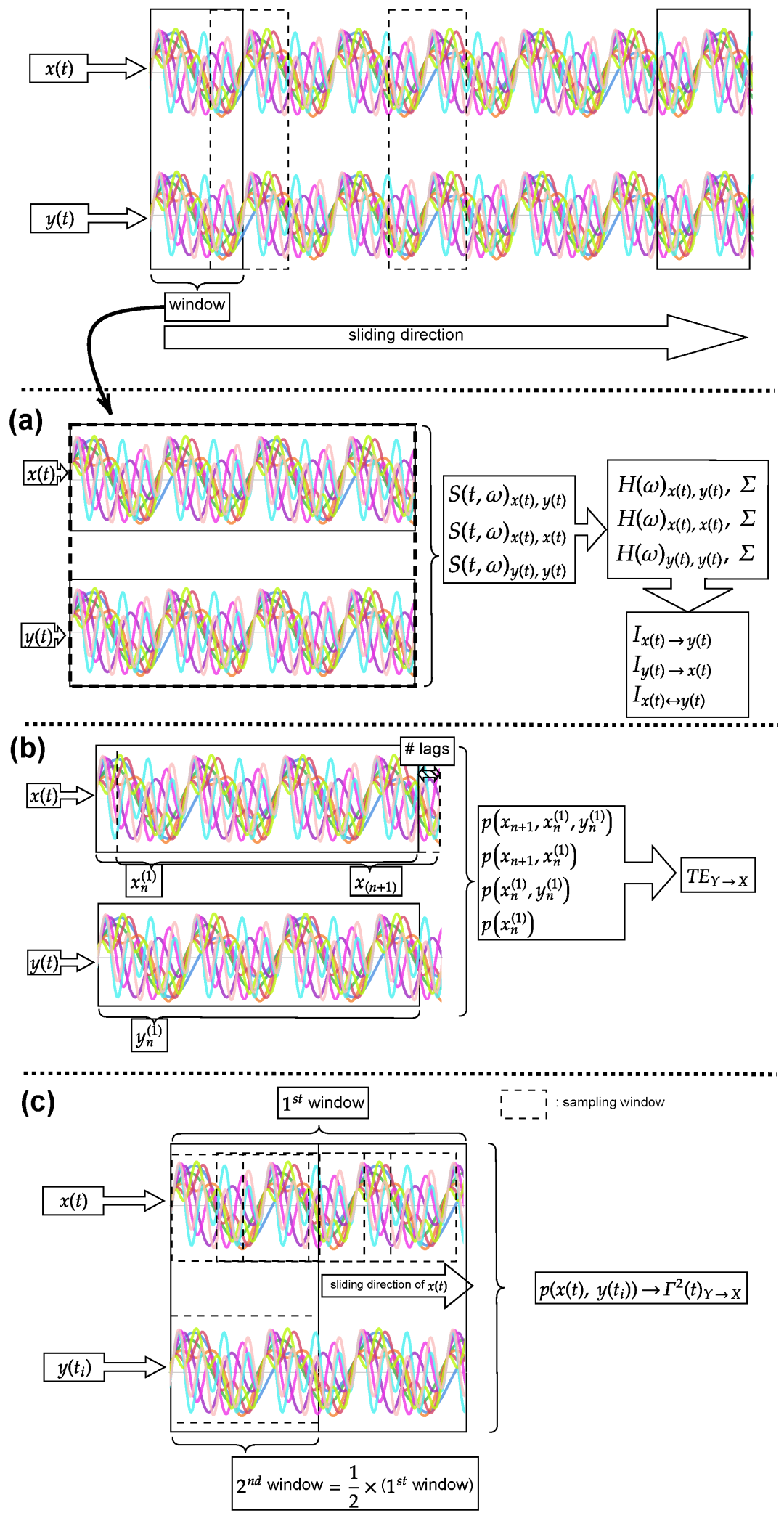
在这项研究中,作者提出了一种通过信息几何来量化因果性的替代方法,克服了这些限制。对于时间依赖的概率分布,可以通过信息速率和信息长度来测量随着时间变化的分布。信息速率(Γ(t))度量了分布变化的速率,而信息长度(𝓛)度量了分布的总变化。为了研究因果关系,作者考虑了两个随机过程 x1(t) 和 x2(t) ,并评估了联合概率分布的信息速率。这些过程之间的因果关系可以通过信息速率的变化(统计变化或分布的变化),同时让另一个过程保持不变来量化。例如, x2(t) 引起 x1(t) 的信息速率被定义信息速率因果性。
图1. 上:不同方法量化因果性的实现过程。(a)GC来量化因果性的实现过程;(b)TE来量化因果性的过程;(c)信息几何来量化因果性的实现过程,图像中每种颜色的线条都代表了不同的模拟。在本研究中,每个窗口包含0.5s的数据点,并与前一个窗口重叠0.25s。因果关系分析在每个窗口内进行。这里将ti表示为在过程中保持不变的参考时间。因此,p(x1(t), x2(ti)) 是通过在时间ti保持过程x2(t)静态的情况下对过程x1(t)随时间t演变而采样的概率分布。由于信息速率只能量化分布中的变化,因此信息速率因果性是在感兴趣的每个时间窗口内评估,而不是在整个时间序列过程中评估,以确定过程之间的耦合是否仍然存在。
作者生成一些通过模拟包含单向和双向时间序列信号中的线性和非线性相互作用的不同类型的离散自回归模型生成的数据,来去对比三种方法的效果。他们的研究结果显示,信息速率因果性在本文探讨的多个示例中能更好地捕捉线性和非线性数据的耦合,优于GC和TE。
图2. 上:不同模型中GC、TE和信息速率因果性的性能。一般来说,GC在线性和平稳信号下表现良好;只有在选择正确的滞后时,TE表现良好;信息速率因果性表现良好,可以恢复信号的潜在滞后。
6. 使用收敛交叉映射
推断环境因素与呼吸道感染之间的因果关系
论文题目:Inferring a Causal Relationship between Environmental Factors and Respiratory Infections Using Convergent Cross-Mapping
论文地址:https://www.mdpi.com/1099-4300/25/5/807
作者:Daipeng Chen, Xiaodan Sun, Robert A. Cheke,西安交通大学,荷兰莱顿大学,英国格林尼治大学
人群中呼吸道感染的发生率与许多因素有关,其中环境因素如空气质量、温度和湿度引起了广泛关注,特别是空气污染在发展中国家引发关切。尽管呼吸道感染与空气污染之间的相关性众所周知,但建立它们之间的因果关系仍然很困难。最近的研究揭示了在气候变化期间呼吸道感染和环境因素之间存在广泛的相关性。尽管相关性并不意味着因果关系,但在复杂系统中,相关的变量可能潜在地共享信息并增加系统的复杂性。
为了解决系统过于复杂难以参数化的问题,研究人员开发了一种称为经验动态建模(EDM)的非参数框架,旨在使用观察到的时间序列来分析复杂系统。在EDM方法中,收敛交叉映射(Convergent Cross-Mapping,CCM)专门用于检测复杂系统中的因果关系。
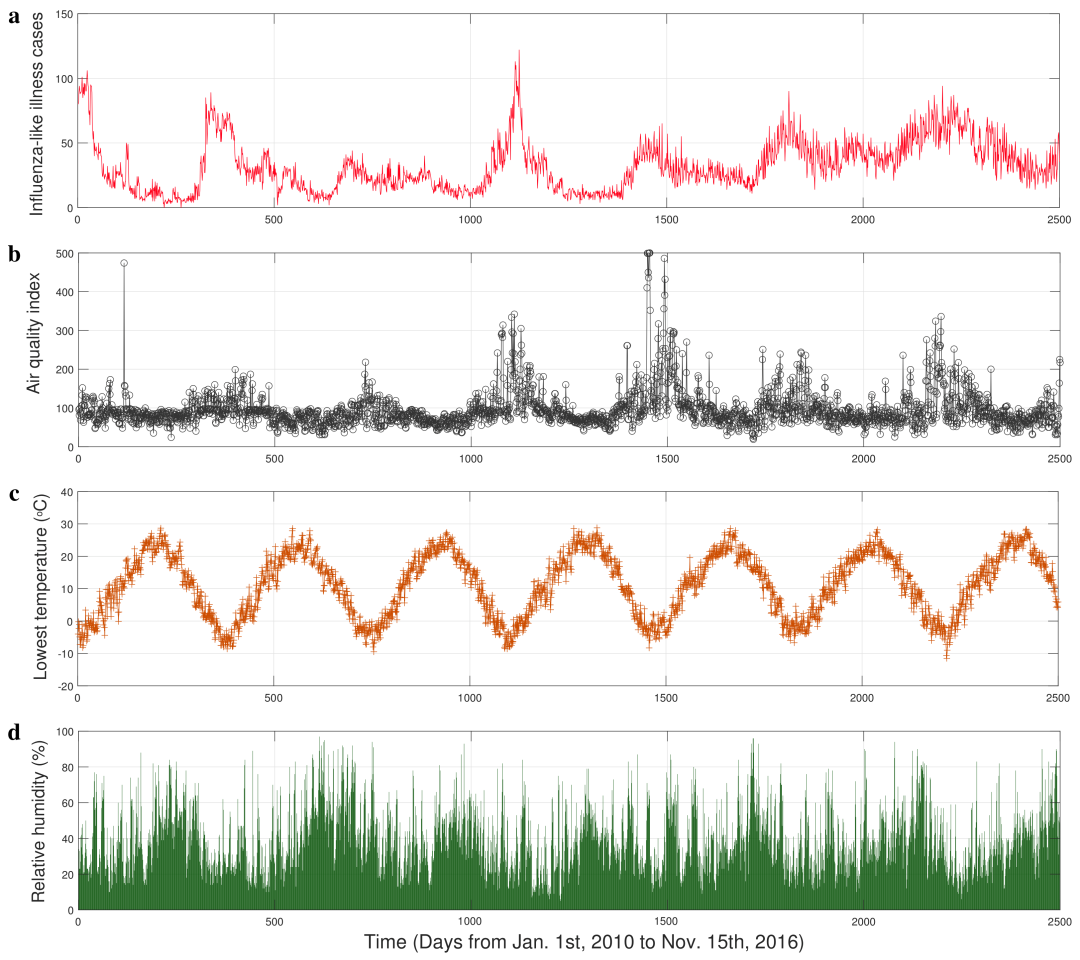
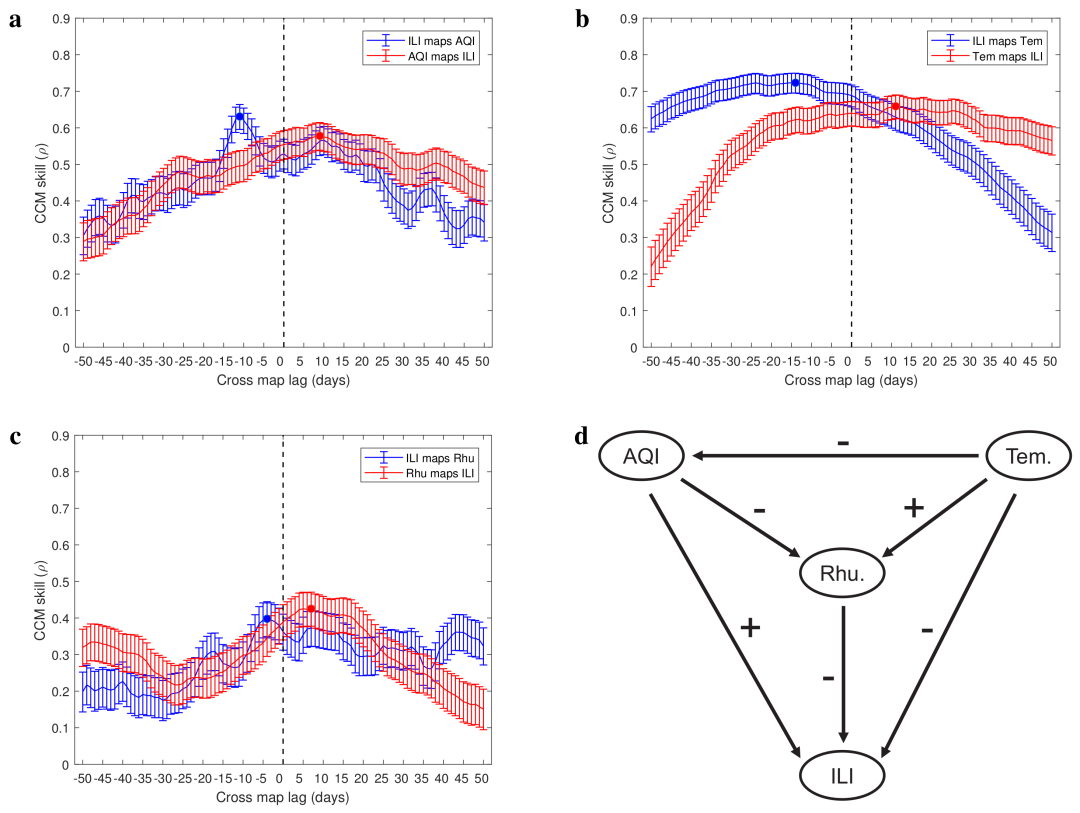
研究人员在数学模型生成的合成数据上验证了这个新过程。对于中国陕西省2010年1月1日至2016年11月15日的真实数据,首先通过小波分析调查流感样疾病病例、空气质量指数、温度和湿度的周期性来确认改进后的方法适用。接下来说明了空气质量(由AQI量化)、温度和湿度对日常流感样疾病病例产生影响,并且特别是呼吸道感染病例随着AQI的增加而逐渐增加,并且存在11天的时间延迟。
图1. 西安市流感样疾病(ILI)病例和实验因素的时间序列图。(a) 从七家医院收集的流感样疾病(ILI)病例;(b) 实时空气质量指数(AQI);(c) 最低日温度;(d) 相对湿度。
图2. 四个变量(流感样疾病病例(ILI)、空气质量指数(AQI)、温度、湿度)之间的因果关系证据。
7. 基于核格兰杰因果性的
精神分裂症 MEG 网络分析
论文题目:Schizophrenia MEG Network Analysis Based on Kernel Granger Causality
论文题目:https://www.mdpi.com/1099-4300/25/7/1006
作者:Qiong Wang,Wenpo Yao, Dengxuan Bai, Wanyi Yi, Wei Yan, Jun Wang,南京邮电大学,南京医科大学
网络分析是探索不同病理生理条件下复杂脑结构的重要手段。为了分析这些结构,我们首先需要构建可解释的网络。该工作作者采用多元非齐次多项式核格兰杰因果(MKGC)来构建有向加权网络,来表征精神分裂症患者的脑磁图特征(MEG)。
作者首先基于耦合自回归过程生成数据,并与二元线性格兰杰因果和二元非齐次多项式核格兰杰因果方法进行比较,检验MKGC方法的有效性。测试结果表明,MKGC优于其他两种方法,具有更好的非线性表征能力。随后,作者将MKGC方法应用于构建精神分裂症(SCZs)患者的有效连接网络。
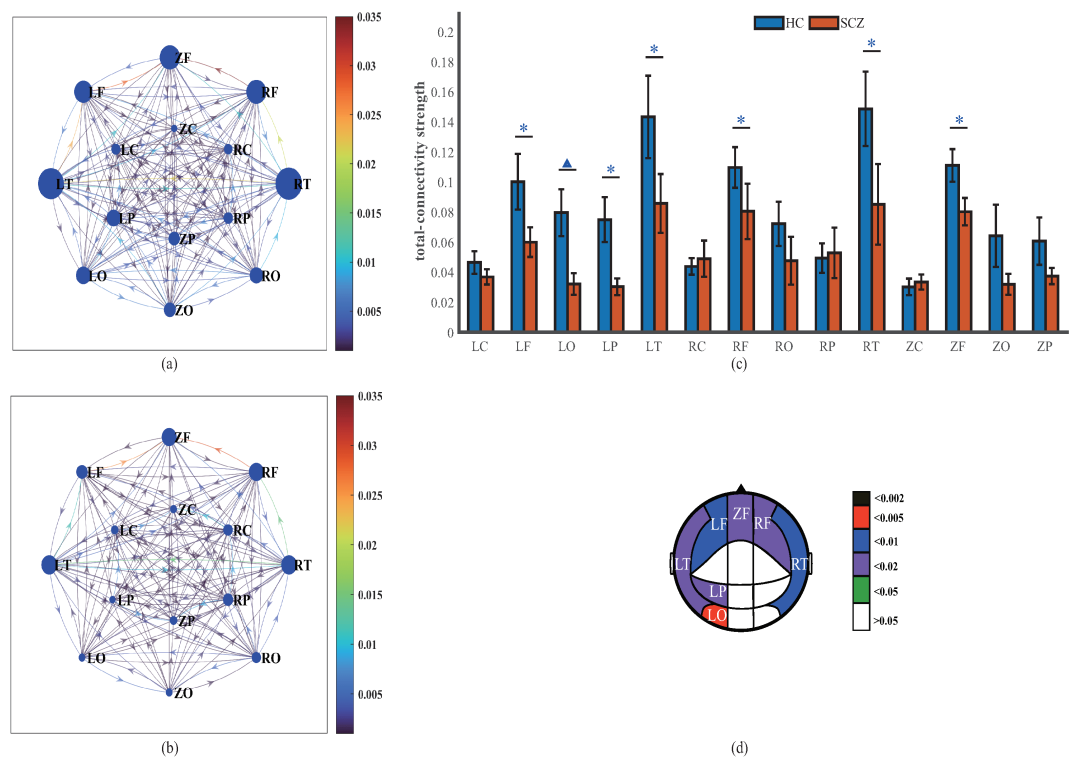
作者测量了三个网络特征,即强度、非均衡性和复杂性,来表征精神分裂症的 MEG。研究结果表明,相比精神分裂症患者,健康对照 (HCs) 具有更密集的有效连接网络。在连接强度方面,最显著的差异出现在右侧额叶网络 (p = 0.001)。所有受试者的外连通性最强发生在颞区,组间差异最显著的是左枕区 (p = 0.0018)。健康对照组的大脑皮层的额叶区、颞叶区和枕叶区的总连通性强度高于精神分裂症患者。SCZs患者的全脑非平衡特征显著高于HCs组 (p = 0.012);然而,香农熵的结果表明,健康对照组网络比精神分裂症患者的具有更高的复杂性。
总之,结果表明SCZs对大脑网络的相互作用有负面影响,基于MKGC的网络分析方法可以为识别SCZs脑网络的动态结构和探讨SCZs的病理生理机制提供可靠的方法。
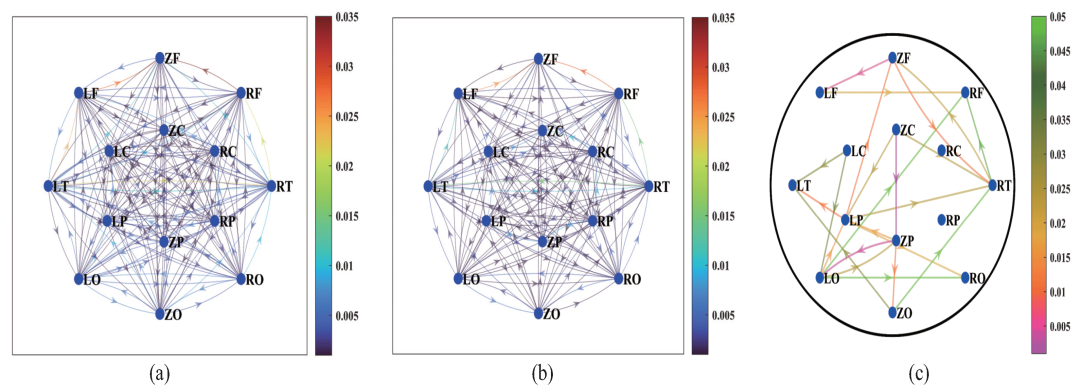
图1. 健康对照组HCs (a) 和精神分裂症患者SCZs (b) 在脑区层面的有效连通性网络。图中节点表示14个脑区,节点间的连接表示脑区间因果关系,箭头表示连接的方向。
图2. 大脑区域之间的总连通性(total connectivity)。可以看到不同大脑区域的总连通性强度差异巨大(d)。
新信息论:从分解到整合
因果涌现读书会第四季招募中
什么是意识?意识能否度量?机器能否产生意识?对于意识问题,人们可能即将迎来一个大的突破,各种有关意识的理论正如雨后春笋般展现出勃勃生机。其中神经科学家 Giulio Tononi 的整合信息论(IID)被认为是最有前景的意识理论之一。如果说意识是大脑神经活动的一种涌现结果,那么刻画涌现便成为理解意识过程中一个重要环节。因果涌现理论目前发展出两个派别,除了 Erik Hoel 的有效信息因果涌现框架,还有一个是 Rosas 的信息分解(PID)框架,此后 Rosas 基于此进一步提出融合整合信息论的信息分解框架 ΦID,尝试构建新的意识理论。
一边是信息整合(IIT),一边是信息分解(PID),看似分裂,实际上都是对香农经典信息论的进一步发展。因果涌现读书会第四季「新信息论:从分解到整合」由北京师范大学系统科学学院教授、集智俱乐部创始人张江老师领衔发起,旨在梳理信息论领域的发展脉络,从香农的经典信息论开始,重点关注整合信息论和信息分解这两个前沿话题,及其在交叉领域的应用。希望通过对这些“新信息论”度量指标的深入探讨,帮助我们理解什么是意识,什么是涌现,并找到不同学科,不同问题背后的统一性原理。
点击“阅读原文”,报名读书会

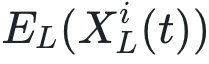 ,能够在给定初值
,能够在给定初值 的条件下确定未来每个时刻的值
的条件下确定未来每个时刻的值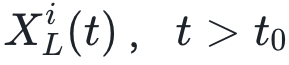 。
。