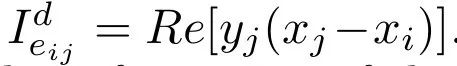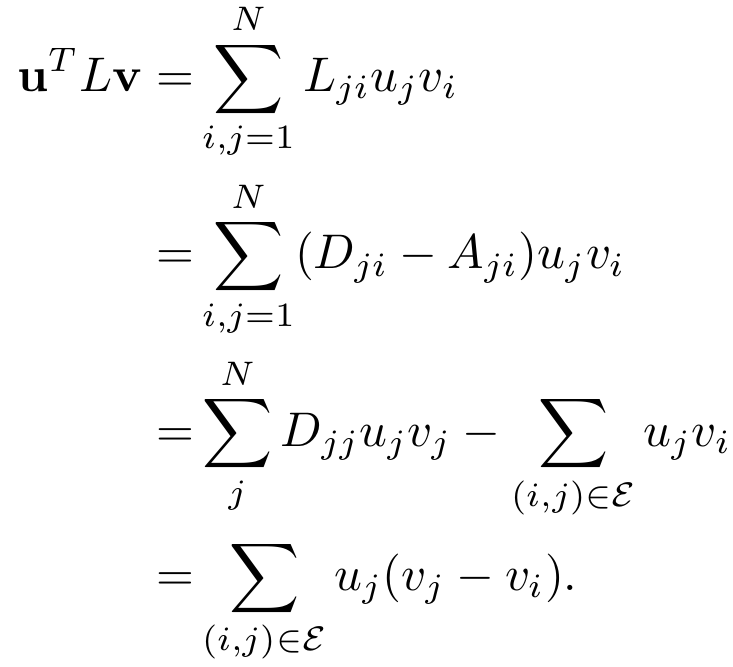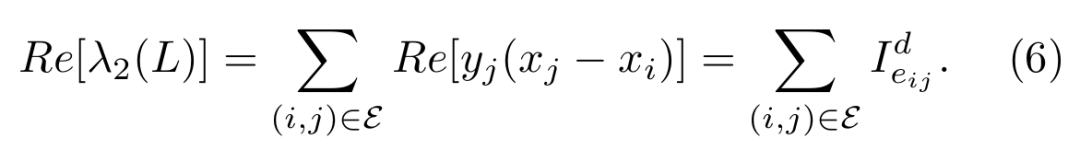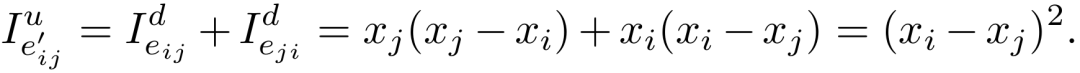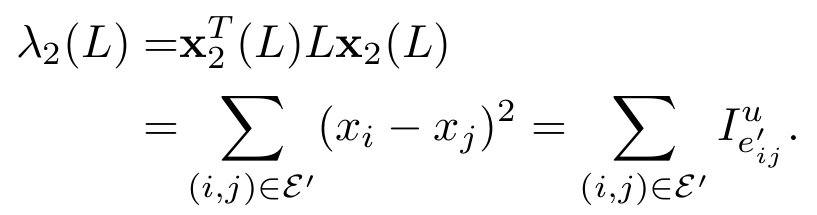PRE前沿速递：复杂网络中有向边的动力学贡献值

导语

寻找网络中的关键节点和关键边是网络科学中的一个最重要、最基本的问题。基于动力学的复杂网络节点中心性已有不少研究，而基于动力学的网络边中心性或交互的中心性成果相对匮乏。去年我们在PRL发表了关于无向网络边和圈的重要性量化工作 [1]，事实上复杂网络有向交互比无向交互更赋挑战性，同时也带了更多的变化和趣味性。例如，无向网络中的边对于网络动力学一定是正向的贡献，但在有向网络中的边是否一定也是正向的贡献呢？如何判断有向边是正向贡献还是负向贡献？具体贡献为多少？有向边的位置和方向如何影响动力学？近日发表于PRE的这篇文章通过分析Fiedler值（Laplacian 矩阵非零最小特征值的实部），回答了这一系列问题。

关键词：有向网络，边重要性，网络动力学，二八律

陆君安、周进、蒋思杨 | 作者

本文介绍我们最近发表在 PHYSICAL REVIEW E 上的论文 :

论文题目：

Fiedler value: The cumulated dynamical contribution value of all edges in a complex network, Phys. Rev. E 109, 054301 (2024)

论文地址：

https://doi.org/10.1103/PhysRevE.109.054301

论文作者：蒋思杨、陆君安、周进、代勤瑞

网络科学理论已经被广泛应用于生物网络、神经元网络、工业电网、群体智能等重要领域。一个共有的、核心的问题是明晰网络结构对于动力学的影响，这具有十分重要的意义。复杂网络节点重要性已有不少研究 [2]，我们提出了基于一致性动力学节点或者节点组重要性指标，通过图的Laplacian矩阵的删后矩阵 (Grounded) 最小特征值刻画 [3,4]。而网络边的重要性或交互的重要性研究相对较少 [5,6]，我们同样从一致性动力学角度出发，研究无向网络中边、圈、高阶结构的重要性，提出了Fiedler向量排序法作为衡量指标 [1,7,8]。本文中我们进一步将无向边研究推广至有向边，并发现了很多有趣的结论。

一、有向边的动力学贡献值

Fiedler值（Laplacian 矩阵非零最小特征值的实部）是网络一致性动力学中的重要指标[9]，用于衡量网络的同步能力、扩散速度等。本文我们将基于Fiedler值定量分析复杂网络中每一条有向边的动力学贡献。

有向边的重要性受位置和方向的影响，如何给出某一指标同时包含这两个信息？我们利用网络动力学和非对称矩阵特征值扰动理论[10]，导出衡量网络中有向边对动力学的敏感性指标。设网络中的有向边为e_ij，表示i→j，对边施加扰动ω，扰动后的Fiedler值的一阶变化量为：

这刻画了边在权重动态变化时对网络动力学的影响，越敏感的边越重要，越容易影响网络的动力学。因此我们将一阶变化量定义为边的动力学贡献值：

其中x为λ₂(L)对应右特征向量，y为λ₂(L)对应左特征向量，我们称之为左右Fiedler向量，它们共同提供了边贡献值的位置信息和方向信息。右特征向量提供了有向边起点和终点的信息，左特征向量仅提供了终点的信息。进一步地根据拉普拉斯矩阵的特征：

我们得到了Fiedler值在网络科学框架下的描述。Fiedler值可视为网络中所有有向边动力学贡献值之和：

如此，一个代数意义下的等式被赋予了网络动力学的意义。我们不仅提出了每条边的动力学贡献值，还得到了所有边值的总和为网络动力学的经典指标Fiedler值。那么，每条边对Fiedler值的贡献便得到了清晰的量化。

二、无向边的动力学贡献值

无向网络是特殊的有向网络，左右Fiedler向量相同。我们将无向边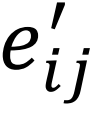的动力学贡献值定义为两条有向边（e_ij和e_ji）的贡献之和：

结果与直接对无向边整体进行扰动分析一致[5,6]，无向边消除了方向信息，只有位置信息，由Fiedler向量决定。进一步地，我们同样得到：

无论是有向网络还是无向网络，Fiedler值均可视作网络中的所有边动力学贡献值之和。并且该结果对于加权网络依然成立。

三、仿真示例

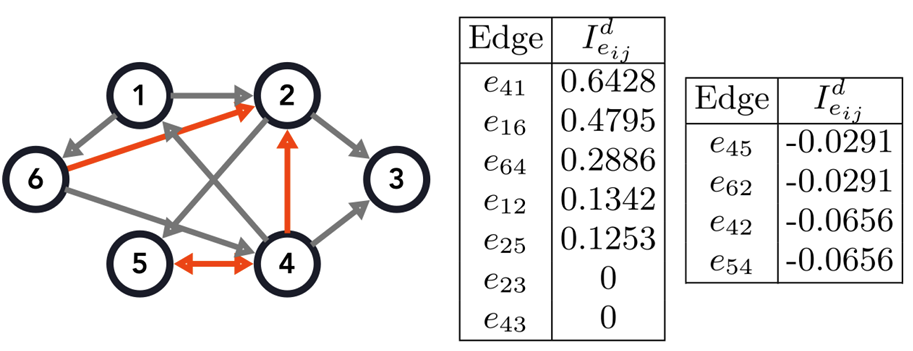
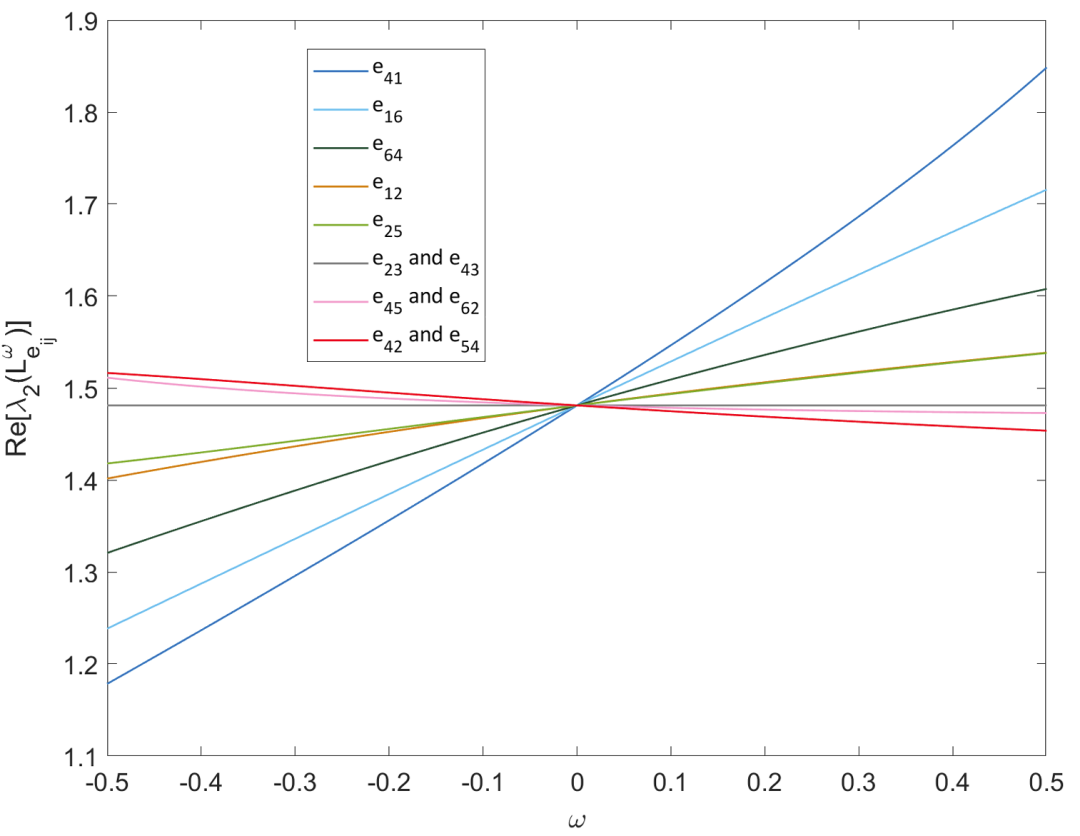
我们首先在图1中检测了一个有向网络的边动力学贡献值，不仅有效识别出了网络中的负向贡献边，并且发现尽管定义要求充分小的ω，仿真显示贡献排序依旧稳定在一个相对大的ω范围。此外，验证了所有边的动力学贡献值求和为Fiedler值Re(λ₂)=1.4811。

图1 一个有向网络中边的动力学贡献值及其-依赖性仿真

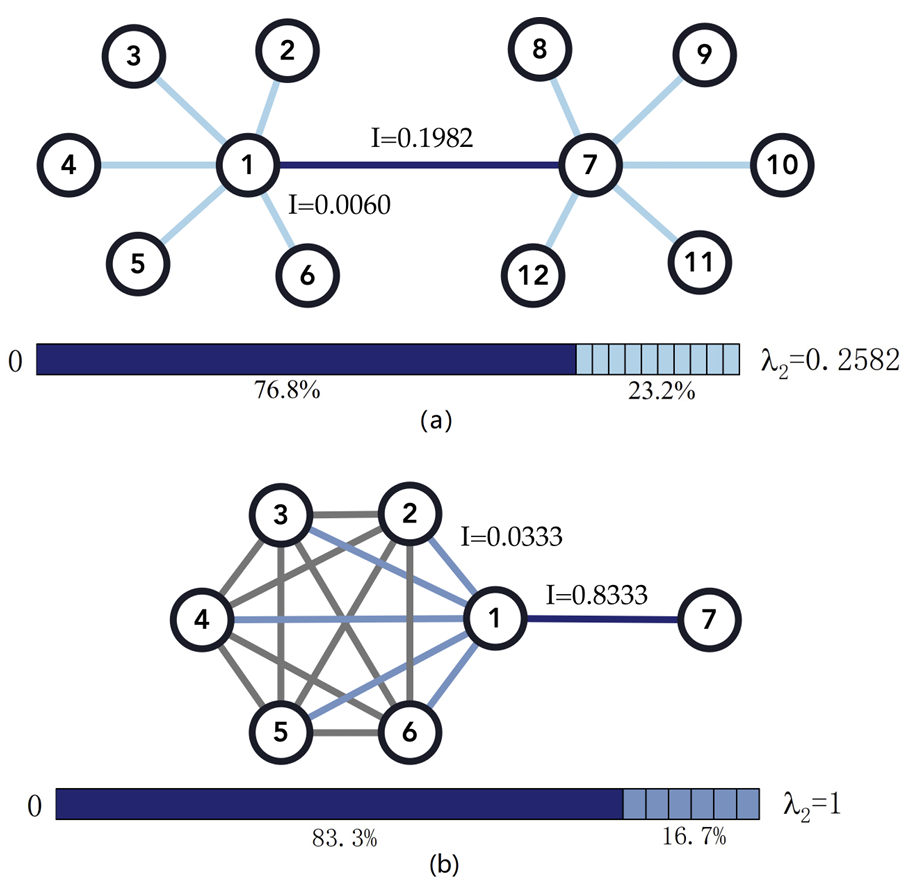
图2 两个无向网络中边的动力学贡献值及其对应的动力学贡献百分比

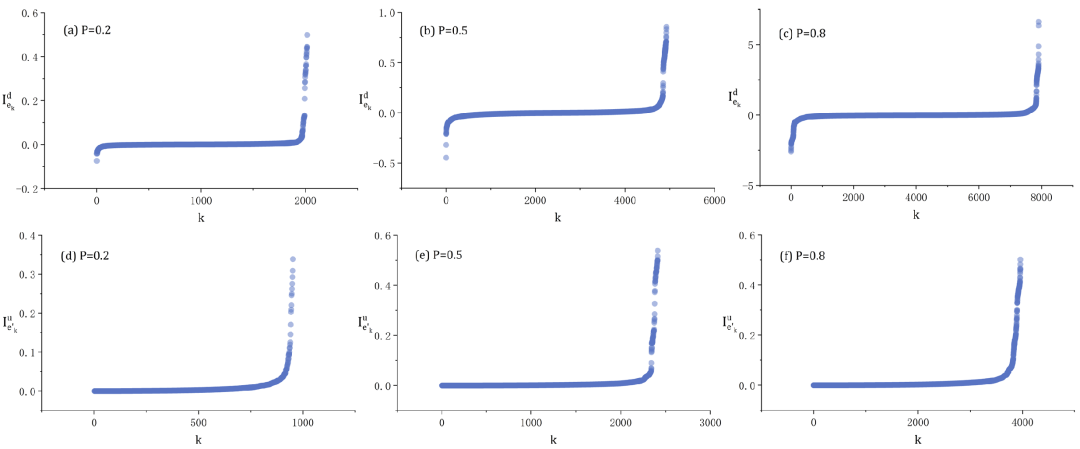
接下来我们在图2中验证了两个典型的无向网络的相关结果，结果与我们的直观感受符合，并发现在这样的度差异较大的网络中，往往少数边占大比例的动力学贡献值（边贡献的“二八定律”）。进一步地，我们在图3中对度差异相对较小的随机网络中检测了所有边贡献值的分布情况，结果同样验证了边贡献的“二八定律”：网络中大部分边对网络动力学的贡献值占比很少，极少数边对网络动力学贡献值占比很大。并且对于有向边来说，存在负向贡献的边，虽然这样的边为数不多，但对网络动力学有着负面影响。

图3 不同连边概率下随机网络的边动力学贡献值分布图（上：有向网络，下：无向网络）；k为边序号，每一个蓝色点表示一条边的贡献值

最后我们在图4中对实证猫脑网络进行了研究，发现仅一条有向边e_27,25就能占到90%以上的贡献，通过扩散仿真验证了大幅度减小这一条边的权重后，的确能极大地影响扩散速度。同时发现这条边具有鲜明的特征：25号节点本为网络的领导者，现收到了跟随者的反馈（图1中最重要的边也是如此）。这些发现可望在真实场景中得到进一步应用。

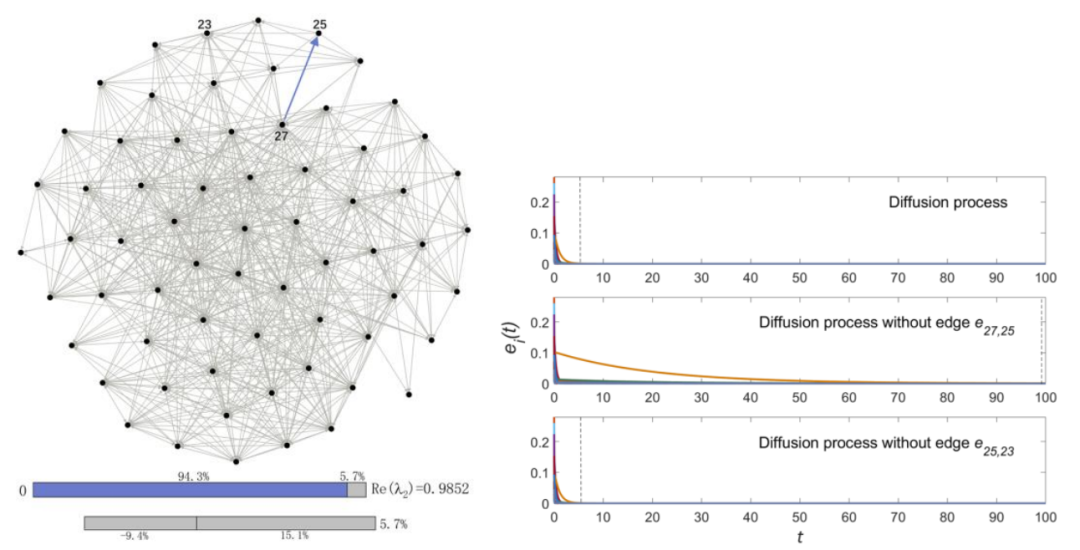
图4 猫脑网络中边动力学贡献图及扩散仿真（从上到下依次为原网络的扩散仿真，以及在大幅度减权最重要边e_27,25(94.3%)和次重要边e_25,23(0.5%)后的扩散仿真）

总之，文章首次定量刻画了有向边与网络重要动力学指标 Fiedler 值的本质关系。仅需两个特征向量，便可量化网络中所有有向边的动力学贡献；并在网络科学框架下对Fiedler值有了新的阐述。动力学贡献值、动力学贡献百分比对扩散分析、牵制控制同步起指导作用，对于动力学与网络结构关系的研究具有重要的意义。可望在最优网络设计、网络的鲁棒性、脆弱性以及网络攻击和防御等方面得到广泛的应用。

参考文献

[1] S.Y. Jiang, J. Zhou, Michael Small, J. A. Lu, and Y. Q. Zhang, Searching for Key Cycles in a Complex Network, Phys. Rev. Lett. 130, 187402 (2023).

[2] L.Y. Lü, D.B. Chen, X.L. Ren, Q.M. Zhang, Y.C. Zhang, and T. Zhou, Vital nodes identification in complex networks, Phys. Rep. 650, 1-63 (2016).

[3] J. Zhou, X. H. Yu, and J. A. Lu，Node Importance in Controlled Complex Networks, IEEE Trans. Circuits Syst. II Express Briefs. 66 (3): 437-441 (2019).

[4] H. Liu, X. H. Xu, J. A. Lu, G. R. Chen, and Z. G. Zeng, Optimizing Pinning Control of Complex Dynamical Networks Based on Spectral Properties of Grounded Laplacian Matrices, IEEE Trans. Syst. Man Cybern. 51(2): 786-796 (2021).

[5] H.T. Zhang, Z.Y. Chen and X.Y. Mo, Effect of Adding Edges to Consensus Networks With Directed Acyclic Graphs, IEEE Trans. Autom. Control 62: 4891-4897 (2017).

[6] H.T. Zhang, H.S. Cao and Z.Y. Chen, A Necessary and Sufficient Condition of an Interfering Reverse Edge for a Directed Acyclic Graph, IEEE Trans. Autom. Control 67: 4885-4891 (2022).

[7] J. Zhou, Y.Q. Zhang, J.A. Lu and G.R. Chen, Introducing a New Edge Centrality Measure: The Connectivity Rank Index, IEEE Trans. Syst. Man Cybern. 54(5): 2757-2764 (2024).

[8] J. Zhou, B. Li, J.A. Lu, and D.H. Shi, Selection of simplexes in pinning control of higher-order networks, Scientia Sinica Informationis (in Chinese) 54: 708-718 (2024).

[9] X.F. Wang and G.R. Chen, Synchronization in Small-World Dynamical Networks, Int. J. Bifurc. Chaos 12: 187-192 (2002).

[10] J. H. Wilkinson, The Algebraic Eigenvalue Problem (Clarendon Press, Oxford, 1965).

本文作者简介

陆君安：武汉大学数学与统计学院二级教授、博士生导师。在复杂网络动力学、同步控制和识别、多层网络、非线性动力学、混沌及应用数学相关领域取得创新性成果，在Phys. Rev. Lett.、Physics Reports、Phys. Rev. E、SIAM J. Control Optim、SIAM J. Appl Dyn Syst、IEEE TAC、Automatica等期刊上发表学术论文270余篇，引用10000余次，合著4部，H指数47。2014至2019年入选爱思唯尔(Elsevier)中国高被引学者榜（数学类）。曾获2008和2016年度国家自然科学二等奖、2007年度教育部自然科学一等奖、2013年度和2006年度湖北省自然科学一等奖和二等奖、1996年度国务院政府特殊津贴。

周进：武汉大学数学与统计学院教授，博士生导师。主要研究方向为多层网络、高阶网络、同步、控制、非线性系统等等。在SCI、EI发表学术论文57篇，其中第一或通讯作者论文51篇，包括物理学顶刊Phys. Rev. Lett.，控制学三大顶刊IEEE Trans. Automat. Contr. (长文和短文)、 Automatica 和SIAM J. Control Optim. 论文被国内国际引用总计2817次，单篇论文引用前两位分别是758次和657次。曾获国家自然科学二等奖、湖北省自然科学一等奖、教育部自然科学一等奖、全国优秀博士论文提名及湖北省优秀博士论文，主持国家自然科学基金项目四项。2021年在“集智俱乐部”组织的第二期和第三期复杂网络课程中，分别做了题为“复杂网络的同步”和“多层网络及其动力学”的专题讲座。

蒋思杨：武汉大学数学与统计学院2023级博士研究生。主要研究方向为网络重要性结构识别、同步控制、生物网络等。研究成果以第一作者发表在Phys. Rev. Lett., Phys. Rev. E。2021年在“集智俱乐部”组织的第二期复杂网络课程中，参与了“网络同步”的书籍领读。

高阶网络社区

随着对现实世界探索的不断深入，人们发现在许多真实的复杂系统中，组成系统的个体之间不仅存在二元交互关系，也广泛存在多个体同时（或以特定顺序）进行交互，即高阶交互现象。为此，研究人员分别发展出了基于超图、单纯复形、依赖关系等的网络高阶表示模型，为复杂网络分析和研究提供了新的思路。

由电子科技大学吕琳媛老师、任晓龙老师及中国地质大学（北京）管青老师在集智俱乐部联合发起了【高阶网络读书会】。读书会围绕高阶交互网络的基本概念、模型、方法与应用等研究进行研讨，按照「基础理论」+「深入理论」+「案例研讨」的模式展开。读书会第一季已经圆满结束，第二季正在筹备中。现在报名加入可以解锁第一季全部录播视频并加入社群交流。