本文是北京师范大学系统科学学院教授张江老师在参加完2007年 Wolfram 暑期学校后撰写的文章,介绍了计算机科学、数学家和理论物理学家 Stephen Wolfram 的开创性著作《一种新科学》(A New Kind of Science)中的基本概念,从元胞自动机到计算等价性原理,从计算宇宙到虚拟层级、自指。
《一种新科学》作为 Stephen Wolfram 的开创性著作,在人工智能蓬勃发展的今天重新焕发生机。该书探讨的简单程序生成复杂性、计算普遍性和涌现行为等核心概念,与现代AI和大语言模型的基本原理高度吻合。最近社区成员韩司阳等老师积极推动《A New Kind of Science》在国内的翻译出版工作,集智俱乐部联合社区成员韩司阳、章彦博、徐恩峤、张江一起联合发起「《一本新科学》读书会」,从9月1日起,每周日上午10:00-12:00开始系列的讨论,欢迎大家加入读书会,做读书会分享或者认领翻译任务。
本次读书会主要是为了聚集更多对这本书和这套理论感兴趣的探索者一起深度交流碰撞,并组织有能力的研究者一同将这本20年的经典巨作翻译成中文版;同时也是想借此机会,能够深入重读经典,挖掘与当前人工智能和大模型研究有着深刻联系,学习Wolfram的跨学科方法和对自然界模式的研究,为AI算法优化和系统设计提供了新视角。
研究领域:复杂科学,元胞自动机,计算等价性原理,复杂性阈值,通用计算系统,虚拟层级,自指
张江 | 作者
目录
1. 虚拟世界
2. 历史
3. 什么是NKS
3.2 替代系统(Substitution systems)
4. 聆听计算的声音
5. CA模拟股市
6. 关于“黑客帝国”的物理学
7. 计算宇宙之间的纽带
8. 从复杂性走向通用性
9. 计算宇宙中的黑洞
10. 走向现实
2007年1月,著名科学杂志《Nature》第445期刊登了这样一篇文章:《Social Sciences: Life’s A Game》(社会科学:生活就是一场游戏)。主要介绍一小群社会科学家用大型网络游戏进行社会科学研究的工作。无独有偶,2007年8月,著名科学杂志《Science》317卷也刊登了一篇题为:《The Scientific Research Potential of VIRTUAL WORLDs》(虚拟世界中科学研究的潜力)的文章,指出目前正发生在两个大型虚拟世界:魔兽世界(World of Warcraft)、第二生 (Second Life) 之中的事情,尤其强调了一批科学家在其中做的一系列有关社会学和人类学的试验,它们不仅给各种社会研究提供了平台,而且预示了一种崭新的研究科学的方向。
网络游戏、虚拟世界也能成为科学研究方向?一点不假,不是你不明白,这个世界变化快。其实,早在2002年,一名叫做Edward Castranova的经济学家就突发奇想,将网络游戏Everquest视为一个真实的在线王国而计算它的GDP,结果发现,它的总量排名世界第14位!不管我们愿意不愿意,网络游戏已经成为了一种不可小觑的力量而存在。我们需要认真、严肃地对待这一现象了。
然而,真正的科学研究需要抛开那些眼花缭乱的3D模型和天方夜谭的游戏故事,究竟什么才是一个计算机模拟的世界?为什么计算机可以创造这些眼花缭乱的虚拟世界?这需要从最最简单的计算宇宙模型开始。
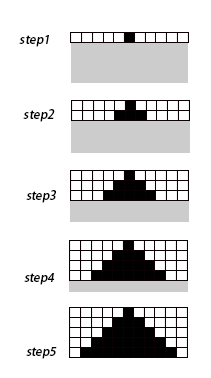
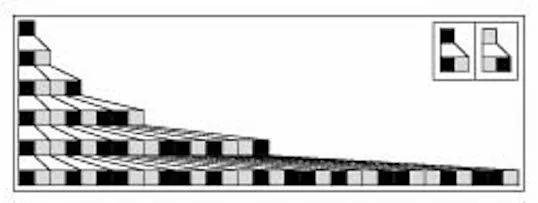
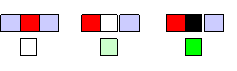
考虑一排方格,每个格子都有黑、白两种颜色,如下图:
其中黑色的方格有左右两个邻居(用灰色进行表示)。那么每个方格就可以根据它的两个邻居以及它自己的颜色按照一定的规则而改变颜色,例如,一个可能的规则如下:
这是一个规则列表,第一排为所有可能的三个输入方格的颜色,下面的一排表示根据这些不同情况,中心的方格应该变成什么颜色。例如第三个规则上面是黑白黑,下面是黑,则当一排方格中有三个方格刚好是黑白黑的时候,中心的方格就变成黑色。
这样,一排方格之中的每一个都可这样按照此规则更新自己的颜色而得到一排新的方格排列,进一步,我们可以再次应用这组规则到新得到的方格上,这样又会得到一排新的方格。可以不停的重复下去……
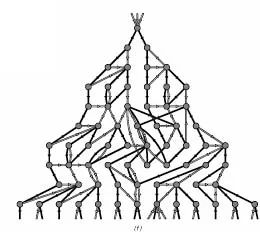
如果我们把每次应用规则得到的方格排成一排一排的,就可以得到下面的图:
我们可以很容易将这个游戏的玩法编成程序,在计算机上实现它。这个游戏的学名叫作元胞自动机(又称细胞自动机,英文是:Cellular Automata, 简称CA)。然而这跟我们要探讨的网络游戏、大型计算机虚拟世界有什么关系呢?实际上,这个程序就是一个虚拟世界的简单原型。(有关元胞自动机的详细介绍,请看这里:http://www.swarmagents.com/complex/models/ca.htm)
我们知道,所谓宇宙就是指空间和时间的总合。空间中的物质按照物理规则运动。那么,在这个简单的元胞自动机中,这一排方格就是宇宙的空间,不同颜色的方格相当于宇宙中的物质,那个更新规则就是这个虚拟宇宙空间中的物理规则。而每一步更新就可以看作是宇宙时钟的一次嘀嗒。因此,空间、时间、物理全都有了,它就是一个最简单的人造的虚拟世界。
我们所生活的真实宇宙只有一个,它的物理规则也是固定死的。然而,对于人造的虚拟宇宙来说,我们就相当于是上帝,拥有了更改物理规则的权利,这样,我们可以通过改变规则而创造出各种不同的宇宙,例如,我们把规则改为:
显然,不同的规则能够创造不同的虚拟世界。有了虚拟世界的最小的模型,我们就能够进行科学分析来。我们可以像物理学家一样做实验,看看在不同的物理规则下,宇宙会是什么样子的。我们可以像生物学家一样对虚拟世界中的各种花纹“生物”进行分类,等等。就好比当年伽利略发明望远镜一样,有了元胞自动机这个最小的虚拟宇宙,科学家们就可以打开一扇窗,去观察另一种完全不同的虚拟世界了。研究这门科学的学问就叫做 A New Kind of Science (一种新科学,简称NKS),他的创始人就是大名鼎鼎的史蒂芬·沃尔弗莱姆(Stephen Wolfram)。
任何一门学科的发展都有其历史,而有关元胞自动机这样的虚拟宇宙的研究则可以追溯到上世纪的一名伟大的科学家:冯·诺依曼(von Neumann)。我们都知道冯·诺依曼是第一台计算机的设计师,还是博弈论的创始人,但很少有人知道,在他的晚年(大概1940年左右),他在研究一个有趣的课题:人造机器的自我繁殖。

Von Neumann 和他的著作《Theory of Self-reproducing Automata》
冯·诺依曼考虑一台机器在一个充满了各种机器部件的池塘里面游来游去,它可以拾起一些部件,并将不同的部件组装到一起……,那么,有没有可能一台机器将不同的组件组装到一起形成一个新机器,而这台新机器和它自己是一模一样的呢?这样的机器就是一台能够进行自我繁殖的机器!
有了这个目标,冯·诺依曼却在自己的科研进展中遇到了障碍。一个关键问题是,当时的人工机器部件非常昂贵,要开发出一台真正的能够自我繁殖的机器需要耗费大笔的资金。这个时候,他的好朋友——一个名叫乌拉姆(Ulam)的数学家给他提供了一条宝贵的建议:为什么不在一个虚拟的世界中创造你的自繁殖机器呢?就比如一个二维的棋盘世界?
对呀,虚拟世界有很多好处,其中最大的好处就是可以省去大笔的经费。于是,冯·诺依曼采纳了乌拉姆的建议,真的在一个二维的虚拟世界中设计出了这样一台能够自我繁殖的机器。后来,人们就将这个二维的虚拟世界模型叫做二维的元胞自动机。
冯·诺依曼的这一工作影响了后来的很多人,包括著名的遗传算法之父 John Holland,人工生命之父 C.G. Langton,还包括当时还很年轻的 Wolfram。

Wolfram是一个具有传奇经历的人,他于1959年出生在伦敦,曾就读于牛津大学。15岁的时候,他就发表了第一篇学术论文;22岁的时候,由于他的杰出成绩而获美国著名的Mac Arthur大奖,并成为此奖项最年轻的获奖者。后来,他曾先后到普林斯顿高级研究院、伊利诺伊斯大学当教授,专职从事科研。
在1980年代中期,Wolfram从早期的高能物理研究领域转向了用计算机探索复杂性科学的研究,正是在那个时期,他发表了多篇有关一维元胞自动机理论的论文,而奠定了他在该领域的权威位置。然而,正当他的学术生涯蒸蒸日上的时候,Wolfram 毅然辞去了他在伊利诺伊斯大学的教职,原因是当时的大学体制很难专门拨经费支持他在元胞自动机这个“怪异”的领域中的研究。
虽然 Wolfram 放弃了他辉煌的学术生涯,却开辟了另一片崭新的天空。他于1986年亲手创办了以他自己命名的Wolfram Research公司,开始开发著名的数学软件Mathematica,并凭借着该软件的商业成功而成为亿万富翁。然而,就在他商业刚刚成功的时候,他却毅然再次走进了书房,在计算机前摆弄起了计算机程序,因为元胞自动机、复杂性科学对于他来说太诱人了!
就这样,在1991年第二版Mathematica面世的时候,他躲进了书房开始了长达10多年的写作。终于,2002年5月,A New Kind of Science 面世了。这本洋洋洒洒的厚达1000多页的大部头创造了多项奇迹:整本书很少看见数学公式,而全部用图形进行科学推理甚至证明;全书分成正文和批注两部分,而批注却占据了1/3的空间;整本书没有参考文献,所有的历史相关工作介绍都放到了批注中;书中提出了很多大胆的猜想,如:我们生活的世界就是一个被计算机模拟出来的世界等等。Wolfram的过火挑衅行为惹毛了美国学术界。然而,这并不影响该书的流行,甚至一跃成为当年亚马逊网站的销量排行首位。
就是这样,在一片唏嘘和争议声中,Wolfram的新科学走过了五个年头。然而,Wolfram的新科学究竟在讲什么?他能给复杂性科学多少本质的贡献呢?让我们来正式开始我们的NKS之旅。
很多人都认为,NKS就是一个研究元胞自动机的科学。事实上,这种认识是不完全的。如果用一句话概括,那么NKS就是一种研究各种“计算宇宙”的科学。而所谓的“计算宇宙”,就是指由各种简单的计算机程序创造的世界。我们来看几个例子:
3.1 图灵机
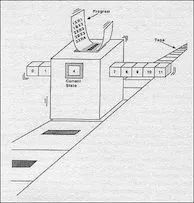
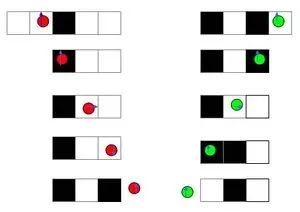
我们都知道阿兰图灵这个人,他最早提出了计算机的原型:图灵机。所谓的图灵机就是指一个抽象的机器,它有一条无限长的纸带,纸带分成了一个一个的小方格,每个方格有不同的颜色。有一个机器头在纸带上移来移去。机器头有一组内部状态,还有一些固定的程序。在每个时刻,机器头都要从当前纸带上读入一个方格信息,然后结合自己的内部状态查找程序表,根据程序输出信息到纸带方格上,并转换自己的内部状态,然后进行移动。
在NKS中,我们可以把不同时刻的纸带像一维元胞自动机一样排在一起形成一个二维的世界。而机器头可以用一个黑点表示,如图:
小黑箭头就是图灵机的读写头,它会在纸带上移来移去画出漂亮的折线。机器头的不同状态对应这个小黑箭头的不同朝向,而机器头遵循的规则就对应了这样一组图标:
这是一个具有两个方格颜色、三个内部状态(分别对应了三种不同的箭头角度)的图灵机。第一条规则表示如果机器头当前读入的方格是黑色的,且内部状态为1,那么机器头就把黑色擦去,并且右移一格,内部状态由1转成2,……
传统的计算机科学将图灵机视为一种计算的工具,即给图灵机编写适当的规则表让它完成某种计算任务,例如计算1+3。但是在NKS中,我们关心的不再是计算任务,而就是观察当给定一组规则后,程序如何行为。也就是说,NKS仅仅关心图灵机在一维纸带上写出的图形。因此,不同的程序在相同的纸带上经过多步计算能够形成非常不同的图形。例如,下面就是一个3种颜色,2种状态的图灵机产生的图形:
我们看到了一副漂亮的图形,它就是用图灵机画出来的。因此,给定简单的规则,放手让程序演化,这就是NKS研究计算宇宙的方法。(有关图灵机的更详细介绍,请参看:http://www.swarmagents.com/vm/articles/turing.pdf)
3.2 替代系统(Substitution systems)
另外一种计算机科学中常用的计算模型就是抽象的重写规则系统,例如,重写规则:A–>AB,B–>BA。从一个字符串开始经过反复重写,可以得到非常复杂的字符串。NKS的研究方法仍然是将不同步骤得到的字符串排成一行一行的,每个字符串都转化成不同颜色的方格,于是,我们仍然能得到一些二维的Pattern(构型),如上面提到的重写规则可以得到:
变化不同的重写规则能够得到不同的Pattern,如:
3.3 自然数
上面讨论的计算系统都是对一些抽象元素的操作,然而传统数学中的计算则强调的是对数的操作。那么NKS能不能讨论对数的运算呢?下面就是一个例子,我们从数字1开始,然后用最简单的运算+1进行反复的迭代。显然,我们会得到序列1,2,3,……。这很平淡无奇,但是如果我们把这些数字表示成二进制数,那么我们仍然可以把它们排列成一行一行的方格,其中黑色表示二进制的1,而白色表示0,这样,我们就可以得到下面的图案:
令人吃惊的是,即使这样一个简单的n=n+1的数学操作仍然可以得到一种复杂的自包含的图形结构。所以,新的表达和观察方法往往能够给人们带来意想不到的收获。在NKS中,Wolfram研究了各种各样的简单计算系统,然而所有这些研究都是忘记计算系统的意义和任务,因为只有当我们不再让计算机程序硬性的进行某种运算,而就是给它们提供舞台,放手让它们演化,那么,它们才会用各种各样的花纹来表现它们自己的真实本性。
4.1 元胞自动机的分类
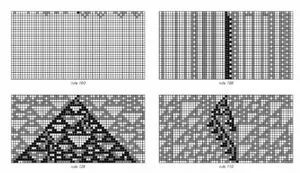
当我们忘掉了比特的意义,给它们释放了自由,我们能做什么才能聆听它们的语言呢?我们要学习生物学家,对计算机生成的各种Pattern分类!早在1980年代,Wolfram就发现,一维元胞自动机在随机的初始条件下所产生的花纹可以归结为4类,它们是:
1. 固定值型:元胞自动机演化到一定时刻就变成了一种颜色的方格;
2. 周期型:元胞自动机固定在具有一定循环结构中不再改变;
3. 混沌型(或叫随机类型):结构在不停的变化,但是它们没有确定的变化规律;
4. 复杂型:这类结构介于完全秩序与完全混沌之间,会产生一些局部的复杂结构,但整体似乎又不是完全混沌随机。
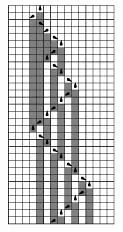
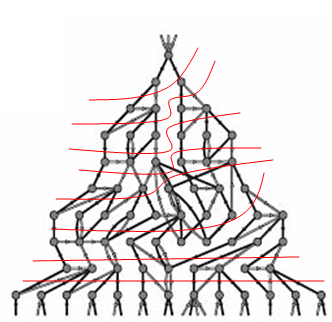
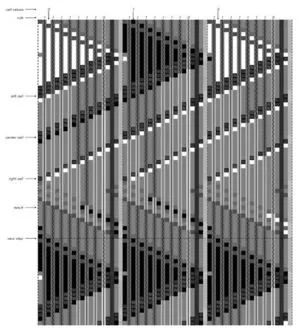
进一步,在NKS书中对这四类元胞自动机又进行了深入研究,例如比较了它们的信息传递情况:
这是四种类型的元胞自动机信息传播的情况。在每一种类型中,我们都运行相同的元胞自动机两次,但是这两次的初始条件略微不同,即唯独中心的方格变化了颜色。那么,我们可以考察这一个变化颜色的方格会对整体元胞自动机的结构产生什么影响。如果在某一时刻某一方格在第二次运行与第一次运行的颜色不同了,则把这个方格涂成黑色。没有变化的方格用白色和灰色表示。
我们看到微小的初始条件扰动会对四类元胞自动机产生不同的影响。对于第一类,这种扰动丝毫没有影响;对于第二类,初始条件的改变对整体的影响会集中在中心的几个方格中不会扩散。而对于第三类,则一个小的改动就会造成大范围的方格颜色的改变,即混沌系统中普遍存在的对初始条件的敏感性。对于第四类,初始条件的改变对整体的影响既不是很大也不是很小。看来从信息传播的机制上来看,这四类元胞自动机还是有着本质不同的。
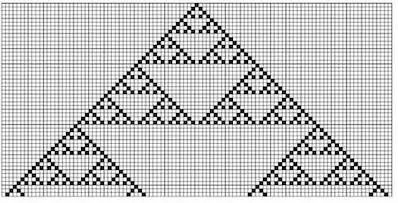
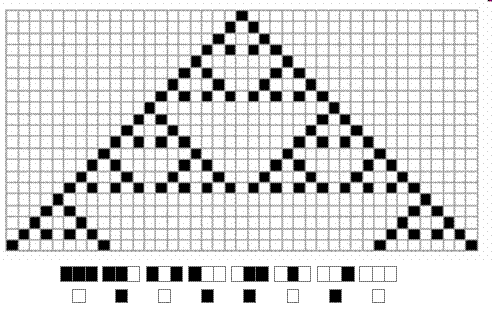
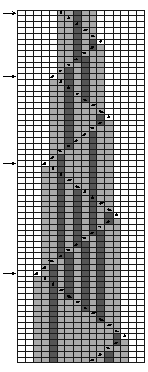
另外,Wolfram 观察到的一个非常普遍的现象是:自相似、自嵌套的分形结构。一个有趣的元胞自动机就是被编号为225的2颜色,2邻居的一维元胞自动机,它在一个黑方格,其他都是白方格的初始条件下能够产生下面的图形:
如果把这个图形作一定的变形:将其以对角线为轴进行反转,并将其扭曲让中间的白色结构靠左边,我们能够得到右边图形:
我们会发现这也是一个大房子套小房子的结构,它和前面提到的二进制表示 n=n+1 的结构(左边)惊人的相似!虽然两套系统的产生规则非常不一样,但是为什么它们却能得到这么相似的结构呢?似乎简单程序们正在向我们传递它们那个世界中的秘密。
4.2 复杂性的极限
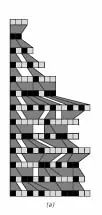
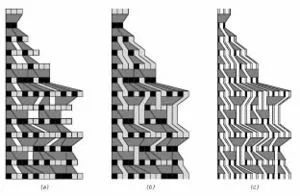
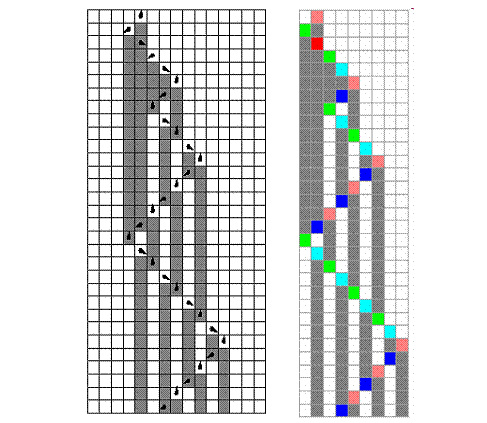
进一步,Wolfram还对各种计算宇宙进行了穷举试验,包括什么图灵机、替换系统、Tag自动机等等,发现:大致上说,这些系统产生的图形也可以归结为那四种类型。而且,最重要的是,系统产生的Pattern的复杂性似乎并不会随着系统规则复杂性的增长而增长。例如,我们一般认为二维的元胞自动机比一维的元胞自动机规则更复杂。然而,当我们把二维的元胞自动机压缩成一维的时候,会看到和一维元胞自动机非常相似的结构。例如,下面就是对著名的二维元胞自动机:生命游戏演化图形的一个一维的截面(这里有一个非常好的探索生命游戏的软件):
该图是这样得到的:将每个时刻生命游戏的运行形成的平面空间排在一起构成一个有高度的三维柱状体,然后对这个柱状体的纵断面切一个截面出来,这样上图纵向就表示不同时刻这个侧面黑白方格的情况,并且将离此截面更远的黑色方格画成灰色,就得到该图。
我们看到,它和1维的第四类型(复杂型)元胞自动机很相似。经过大量的实验,我们似乎可以得到这样一个结论:规则复杂性的增长并不一定会导致行为复杂性的增长。定性来说,如果将两者画成关系曲线,会得到下图:
当规则非常简单(例如所有的方格都变成黑色),它的行为肯定是简单的。这时候我们稍稍增加规则的复杂性,系统的行为也会复杂。然而,当规则的复杂性超过某个特定的程度之后,行为的复杂性就不会增长了。似乎行为复杂性的增长存在一个阈值,系统的复杂性不能超越这个阈值,而无论底层规则多么复杂。这个结论实际上有着非常深刻的内涵,我们在后面的章节中将会指出这个阈值到底是什么。
这个原理的发现,似乎告诉我们。为了建模复杂系统,并不是越复杂的计算机模型越好,因为原则上讲,更复杂的计算机规则并不一定能够导致更复杂的表现行为。
可能更多的人关心的是Wolfram的新科学有什么用呢?这的确是一个很有争议的问题,因为你既可以说NKS非常有用,也可以说它什么都不能做。
我们都知道,简单程序可以模拟自然界的生长现象,例如雪花的形成、树的生长、动物表面上的花纹等等。运用元胞自动机还可以模拟自然界的一些复杂的非线性过程,例如复杂的流体、交通流等。然而,这些应用其实又回到了一般计算机模拟的老路上,即针对具体问题,赋予每一个比特一定的意义,然后让系统去演化。
然而,NKS强调的是忘掉模拟和比特的意义。这样一种哲学会给我们带来什么好处呢?下面这个简单的应用会给我们耳目一新的感觉。
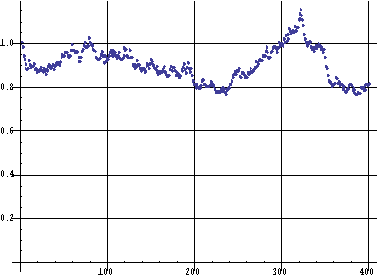
该应用研究是想用CA生成一个时间序列曲线,然后用这个曲线去拟合股票的价格波动,它是由Wolfram公司的研究员Jason做出的。
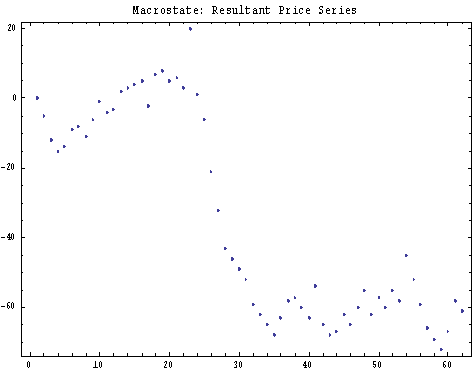
考虑一个特定的元胞自动机,例如CA90(对1维的、邻居为两个的元胞自动机的编号,确定了一个编号就确定了它的一组规则),它形成的图形和一个时间序列曲线,如下图:
上面的是CA90的运行情况,下面的是它生成的时间序列曲线
这个时间序列曲线的具体做法是,将每一步CA90生成的黑元胞方格作为1,白元胞方格作为-1,然后对所有方格求和,得到该时刻的总的数值s(t),然后在下一时刻,同样求得这样一个总和数,把这个数加上s(t),得到s(t+1),这样反复不停的运用这一方法就能得到一个上图所示的时间序列曲线。
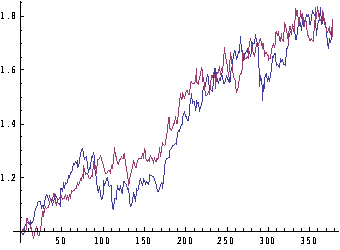
进一步,Jason考虑由两个元胞自动机混合得到的时间序列。例如给定两个元胞自动机CA90和CA110,然后我们把它们进行一定比例的混合。例如混合比例是3:7。具体做法是,从任意一个随机初始条件开始演化3步CA90,然后再演化7步CA110,这样我们得到一个混合的元胞自动机,Jason叫它ICA,用同样的方法,可以画出这个ICA生成的时间序列曲线:
下面,Jason就用这个生成的时间序列曲线去拟合真实的股票价格数据。具体方法可以是通过调节两种元胞自动机的混合比例,例如从3:7调到8:2,使得生成的序列能够和真实数据在均方误差的条件下拟合的很好,如下图:
Jason试了很多种两两元胞自动机组合的情况,都能够得到较好的拟合曲线。然而,很奇怪的是,这个方法并没有对股市建立任何显式的模型。
这个研究的意义在于,即使我们完全忘掉股市运行的内在规则,仍然可以找到拟合股票数据的方法。这反过来说明了复杂的行为并不一定需要复杂的微观机制。仍然是那个观点:从某种意义上说,行为的复杂性增加到一定程度就停止增长了。
注:接下来两部分的内容过于技术化,读者可以有选择的跳过。
相信读这篇文章的人大部分都应该看过《黑客帝国》这部影片。与其他的好莱坞式的科幻电影不同,这个影片具有非常深刻的哲学、宗教内涵,甚至与科学也密切相关。虽然大众一般认为这是一部有关“人工智能”的片子,但是与该影片更相像的科学倒不是传统意义上的人工智能,而是Wolfram的“一种新科学”。黑客帝国中描述的那个大型的控制人类的计算机模拟系统Matrix究竟有没有可能呢?NKS的第9章“基础物理学”对这一问题进行了一系列的探讨。
这一章的基本出发点就是,如果我们就把我们生活的宇宙看作是一个大的模拟系统,那么我们将能够走多远?
6.1 离散的格子
量子力学告诉我们,很有可能在非常微小的尺度上,我们所生活的空间是离散的。也就是说,宇宙的空间从本质上讲就是一张离散的大网。然而,网络是没有维度的,它和我们感受到空间的三个维度不同,这个冲突如何解决呢?答案就在于涌现。首先,我们看一个反问题,即由空间得到网络。这个问题对于搞计算机的人来说并不陌生:即我们如何对一个空间进行有限的划分,从而得到一些基本的单元。例如,对二维平面进行划分有多种方法:方格、六角格等等。下面就列出了三种不同空间的划分:
它们分别是对一维直线区域、二维平面、三维立体空间的划分。给定了这样的一个划分,我们就能得到一个网络。那么这三个不同维度的空间得到的网络有什么不一样的性质呢?
我们可以做这样一件事,任意挑选一个网络上的节点,然后挑选出与该节点相邻的那些节点组成一个集合,计算该集合的元素个数计为 N(1)。之后,再从开始这个节点出发,找出所有的与它相隔两条边的节点组成一个集合,记这个集合的元素个数为 N(2),依此类推……,我们能够得到一个序列:N(1), N(2), ..,N(r)….。如果把相隔半径r作为横轴,把N(r)作为纵轴,不难做出一条 r-N(r) 的曲线。下面,我们来分别对这三个网络求出 r-N(r) 曲线:
这三个曲线分别可以看成是常数曲线、直线和二次曲线,也就是说函数关系分别是:N(r)~r0, N(r)~r1 和 N(r)~r2。而这些网络所在的空间维度分别是1维、2维和3维的,因此,我们能够得到这样一个关系:
这里d是网络镶嵌空间的维度。所谓的镶嵌空间,就是指能够把该网络不重叠的画在一个最小维度的空间之中。因此,三维的网络空间是不可能不重叠地画在二维空间之中的。进一步,我们可以把这个结论抽象为对网络的维度定义。即如果网络中任意一点邻居的个数随着距离的增大而呈现上式的关系的话,那么,我们就可以定义该网络的维度。
我们看到有些网络对应的曲线具有分数的幂律关系如f,因此,也可以说这些网络对应的空间是分数维的。有些网络甚至具有非常不规则的曲线关系,如e,j。
总的说来,如果我们宇宙的空间是由离散的网络构成的,那么它也能够自然导出我们所体验到的各种三维空间的性质。
6.2 因果网络
除了空间之外,宇宙的另一个重要性质就是时间。关于时间,NKS又能说什么呢?首先,我们所体验到的时间是一个一维的长河,宇宙时钟每嘀嗒一次,该宇宙中的所有物体就都同时更新一次状态。这些物体的状态更新就构成了不同的事件。宇宙好像一张大的因果网,不同的事件由于相互之间的因果关系而连接到一起。因此,从时间角度看宇宙,那么一个一个事件就构成了基本的研究单位,并且事件之间由于因果联系构成的网络也成为了某种非常本质的描述。
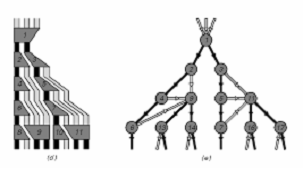
在计算机的各种计算宇宙中,也存在这样的因果联系事件。不同的是,我们可以很方便的用计算机算法得到这些因果网络。例如,有这样一个替换系统:
它也可以写成字符串的形式:A–>AB, BABA–>BB, BBB–>AA,那么从BBB开始,反复应用这三条重写规则,就能得到一个计算宇宙的历史:
其中灰色的带形区域表示了更新规则的计算作用。白色的带形区域连接了两个时刻没有更新变化的方格。通常情况下,我们关注的是方格,但是当我们考虑因果联系网络的时候,我们不再关心方格,而关心的是方格发生变化的事件本身。在这个图中,这些更新事件就表现为灰色的带形区域。因此,对上图进行一系列连续变换,我们不难得到一系列图:
我们看到,这一系列拓扑变换可以把原来的带子变成一些分立的节点,而把原来的方格变成了一些不同颜色的条纹,最终,我们可以把它变成一个网络,其中箭头指向了作为结果的事件:
其中各个更新事件变成了被标号的节点,而方格则变成了联系各个事件的不同颜色的连线边。最后,我们把得到的网络排列成树,即按照离根节点(1号节点)的距离从小到大,从上到下排开,得到:
这就是前面那个替换系统最终形成的因果网络。这个网络有以下几点特征:
1、该网络没有圈状结构。这是因为时间的流逝只能朝一个方向,前面的事件只能影响后面的事件,但反过来则是不可能的。
2、该网络存在着一些边是从底下的节点连向上面的节点的。假如我们是一个生活在该网络之中的生物体,我们并不知道宇宙中的各个事件是如何更新的,我们仅仅能看到事件之间的先后因果顺序。一种可能是,我们把纵向从上到下看作是我们所在的这个宇宙的时间顺序。也就是说,树的第一层节点对应的是第一时刻宇宙发生的事件,第二层节点是第二时刻宇宙发生的事件……。那么从上至下的箭头表示上一时刻的宇宙事件对下一时刻宇宙事件的影响。同层次之间的箭头表示同一时刻宇宙中的两个事件的相互影响。这可以理解成这两个事件具有空间上的联系,因此在同一时刻事件A发生会同时影响到B发生。那么,反向的箭头意味着什么?它意味着未来的事件对当前该时刻的事件的影响。等等,这不是意味着时间在倒流吗?而时间倒流是会引起逻辑上的悖论的。比如说未来的你自己通过时间倒流把现在的你杀死。然而因为现在的你是未来的你的原因,所以你死了未来的你也就不能存在了。
但是仔细思考我们的因果网络会发现,虽然时间倒流在该网络中是可能的,但是逻辑悖论却是不可能的。这是因为在因果网络中不存在任何圈结构,所以,不可能出现两个事件互为因果的可能性。
事实上,给定了这样一个网络,我们还有另外的画它的方法。例如我们可以把它画成另外一棵树,处于两条红色曲线之间的节点作为一个层次。
那么,我们就得到了另一个完全不同的时间。以前同时的事件现在不再同时发生了。然而,有趣的是,这个新的树仍然对应了跟以前一模一样的因果网络。如果我们把不同的展开成树的方法看作是不同的观察者对这个宇宙的观察的话。那么我们会很自然的得出类似相对论的结论:时间是对于观察者而变的,但是事件之间的因果关系则是不变的。
NKS的书中还有很多有关相对论、量子力学的讨论,在这里就不一一列举了。总之,如果将宇宙本身就视为一个离散的计算系统,很多艰深的物理学问题就都获得了新的解释。
通过对大量计算宇宙的观察,我们发现,各个计算宇宙之间有着惊人的相似性,究竟为什么呢?实际上,各个计算宇宙之间存在着非常深刻的联系,这就是它们之间存在着相互模拟的关系。
一台图灵机可以模拟一个元胞自动机,元胞自动机又可以模拟替换系统。只要我们找到了一种将A系统的状态和运算动作一一对应到B系统的方法,我们就说B系统可以模拟A系统。整本NKS书充斥着大量的事实列举和猜测,而唯有讲述模拟的第11章(计算的概念,The Notion of computation)有着相对严格的证明。因为根据模拟关系的定义,只要我们找到了一个计算机程序可以把A系统映射到B系统,那么我们就说B能够模拟A。因此,计算机程序就成为了证明方法。
为了理解什么是不同计算宇宙之间的模拟,让我们来看一个具体的例子。下面是一个特殊的具有3种内部状态,两种方格颜色的图灵机的规则:
下面的问题是,我们能否找到一个特定的半径为1,颜色数不限的元胞自动机来精确模拟这个图灵机的行为呢?答案是肯定的,根据模拟的定义,我们首先要找到一个将图灵机的所有状态映射到元胞自动机的状态的方法。
一个很自然的想法就是将图灵机的纸带映射为元胞自动机的元胞。因此有多少个纸带就有多少个元胞,而纸带的黑白两种颜色就对应元胞的两种颜色。然而,因为图灵机还有一个读写头,这个读写头有着不同的内部状态,这些信息如何找到元胞自动机的对应呢?
一个自然的想法是,增加元胞自动机每个元胞的可能颜色数。因为图灵机的内部状态有1,2,3三种,当它对一个纸带格进行读写操作的时候,就会叠加上这个纸带格上的状态(0或者1)。这样,总的组合情况就是3*2=6种。而对于没有读写头的格子,纸带有0或1两种情况,因此,对于一个元胞自动机的方格来说,只要它能对应这 6+2=8 种情况就可以了。因此,我们可以设计一个具有8种颜色的元胞自动机来模拟这台图灵机。
下面这个表就是图灵机和8种颜色元胞自动机在一个方格上的对应关系:
在该列表中,不同的列对应了不同的图灵机纸带的输入情况,以及相应的元胞自动机的方格颜色。不同的行表示了不同的读写头状态,以及对应的元胞自动机的颜色。黑和白对应了没有读写头在上面的图灵机纸带格,浅红和深红对应了读写头分别在白色方格或者黑色方格,且内部状态为1的元胞自动机的方格颜色,等等。
进一步,要想让元胞自动机模拟图灵机,我们还需要把图灵机的每一步运算都映射到元胞自动机的每一步运算上。一个简单的方法是,针对每一个图灵机的规则,我们都能找到一个或多个元胞自动机的规则与之对应。比如,对于一个图灵机的规则:
它表示在1状态,读入纸带是1的时候,读写头右移一个方格,并把当前格子改为白色。有了前面的状态对应表,我们不难把这一规则转化成如下多条元胞自动机的规则:
其中灰色的方格可以是任意一个颜色的方格。因为红色方格模拟了图灵机读写头读到黑色方格的情况,因此对于元胞自动机来说,无论该红色方格的邻居是何种颜色,它都必须在下一时刻变成白色(第一个图标),同时读写头要移动到右边一个方格。这又有两种可能,第一种是右边的方格原来是白色,这就对应了中间的这个图标;第二种是右边的方格是黑色,这对应了第三个图标。因此,有了这三组规则,我们能够保证元胞自动机可以模拟图灵机的这一规则。
同样的道理,对于其他的图灵机规则,我们都可以找到一组元胞自动机规则与之对应。所以,我们完全可以通过设定元胞自动机的规则而模拟这台图灵机的动作,下面就是这样一次模拟:
这两个系统的动作精确相同。这就是说我们找到了一个元胞自动机能够模拟这台图灵机。不难看出,上面的这种从图灵机到元胞自动机的对应关系是通用的。也就是说,对于任何一台图灵机都能通过此种方法构造出一个特定的元胞自动机来模拟它。因此我们说,一维邻居半径是1的元胞自动机这一类计算宇宙可以模拟图灵机这一类计算宇宙。
不仅仅元胞自动机可以模拟图灵机,图灵机反过来又可以模拟元胞自动机。例如,针对一个特定的邻居半径是1,有两种颜色的编号为90的元胞自动机:
我们可以找到一台6个内部状态、作用到3个颜色的纸带上的图灵机来模拟它。图灵机的工作原理与元胞自动机最大的不同就在于,图灵机是一台串行操作的机器,因为每一时刻读写头只能盯住一个方格,并对它进行改写。但是元胞自动机却可以在一个时刻一下更改所有的方格。如何解决这个矛盾呢?实际上在我们的数字计算机编程实现元胞自动机的过程中,已经可以找到这种利用串行的算法来模拟并行的方法了。基本思想就是让图灵机从左到右扫描所有方格,然后分别对这些方格的颜色进行更新。这样一次来回扫描就刚好完成了一步元胞自动机的运算。也就是说,多步图灵机的运算才对应1步元胞自动机的动作。由于我们允许程序运行任意长时间,所以图灵机可以模拟元胞自动机的全部动作。
下面的示意图就仅仅有6个方格,图灵机模拟CA90的操作:
为了简便起见,示意图仅仅画出了图灵机的读写头在第二个方格起步的情况。实际上,该图灵机有6种内部状态,这6种内部状态分成了2组,一组对应的是从左往右移动的,一组对应的是从右往左移动的。为了表示方便,我们把第一组状态表示成了一个红色的圆圈加上一个向上或向右或向下或向左的指针。同样把第二组表示成了绿色的圈加上不同的指针方向。在每种情况下,这些内部状态都起到了对所读方格的记忆的作用。如左图所示,图灵机头从第二个格出发读入一个方格1,内部状态由1转变为2,这个时候读入第二个方格0,因此这两步串起来就对应了10,它的内部状态转变为3,这个状态3相当于一个内部存储器记住了符号序列10,于是就可以根据CA的规则读入第三个格0,那么输出应该是1,它就把这个1输出出来,打印到第5个方格上。实际上,当前时刻,新的方格状态反映的是左边一个方格在下一个CA时刻对应的颜色(即第5个格子反映的应该是第4个格子的颜色),也就是说图灵机要把左边一个方格的信息暂放在这里。然后图灵机继续往右走。
当从左往右扫描完整个一行之后,读写头开始反着走。这时候,读写头需要做的就是把当前方格的信息(无论是1还是0)都原封不动的拷贝到左边的一个方格去,因此,只要用2个内部状态就可以完成倒着扫描的任务(因为它需要记忆的就是上一时刻0或者1的颜色)。就这样,图灵机一遍一遍的扫描纸带就可以模拟CA的动作了。下图就是该图灵机模拟CA90的情况:
其中灰色的区域表示图灵机头需要扫描的区域(即图灵机走到灰色区域的边缘就可以返回来),因此白色以外的方格是不需要图灵机扫描的。通过这个增加的颜色,就能让图灵机严格、有效地模拟元胞自动机的动作了。箭头所指的一行一行方格表示对应的该图灵机模拟的元胞自动机不同时刻的状态。我们可以把箭头所指的这些行专门挑出来,排在一起,得到:
实际上,这个特定的6状态、3颜色图灵机可以模拟任何一个2颜色,邻居半径为1的元胞自动机。而只要我们能扩充图灵机的内部状态数,不难想象图灵机可以模拟任何一种一维的元胞自动机。也就是说图灵机这个类是可以模拟一维元胞自动机这个类的。
这样,又因为元胞自动机这个类可以模拟图灵机这个类,所以,我们看到了图灵机和元胞自动机的某种相互等价的关系。也就是说,原则上讲如果A和B是完全等价的,那么A能干的事情B也能干,B能干的A也能干。因此,我们就在不同的计算宇宙之间划上了等号。
在NKS一书中,Wolfram证明了各种各样的计算宇宙都是计算等价的,也就是说它们都可以相互模拟,那么它们之间的那种神秘的相似性也就不那么奇怪了。
8.1 通用计算
早在上个世纪30年代的时候,人们就发现了各种计算系统之间由于可以相互模拟所带来的等价性。于是,人们猜想,也许自然中的一切计算都不会超过人们发明的各种计算模型所能及的范围。这个猜想被称为丘奇-图灵论题(Church – Turing Thesis),即:
任何一种可有效计算过程就是图灵机可计算的过程。反过来说,图灵机可计算性就是有效计算的定义。因为,任何一个计算过程都可以用图灵机来计算,因此,人们又称图灵机是一类具有通用计算性,简称通用性的系统。
那么,任何一类可模拟所有图灵机的计算系统也是一类具有通用计算性的系统,或称为支持通用计算的(Universal computation)。
通用性是一个非常重要的概念,它意味着各个不同系统之间的某种本质上的等价关系。例如,我们说英语是一种国际通用语言,这意味着不同的国家都可以通过英语来进行交流。因此不同的国家被通用的英语联系了起来。再例如,我们说人民币是目前中国通用的货币,它意味着不同的商品买卖可以通过人民币联系到一起。因此,系统中有了通用性,该系统内部就有可能形成某种统一的联系。
计算中的通用性无非也为各个计算宇宙联结了纽带。然而,当我们说计算的通用性的时候,它却有两层含义,第一层含义是指某一类系统是通用的。就比如图灵机这个类,它能够完成任何一种计算。
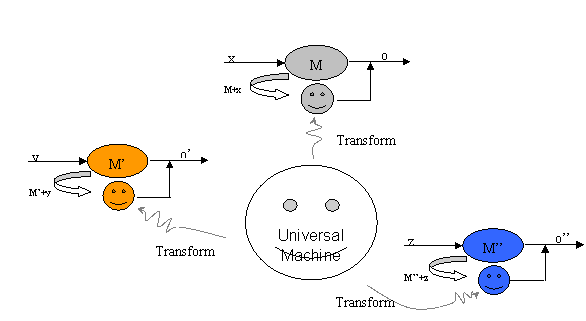
另外一层含义是指,某一个具体的计算系统是通用的。那么这个通用的计算系统就被称为通用计算机。换句话说,通用计算机是一台特定的机器,它能够模拟任何一种其它机器的计算。
历史上第一台特定的通用计算机器是图灵在1936年首先发现的,它被称为通用图灵机。这台通用图灵机的威力在于不用改变它的规则和内部状态数,只要给它不同的输入纸带,它就可以完成任何一台其它的图灵机所能完成的工作。
换句话说,通用图灵机就像一条变色龙,它能够在不同的输入条件下变身成为任何一台其它的机器,如下图式:
在元胞自动机这个大类里面,也存在着通用的元胞自动机,它可以模拟任何一个其它元胞自动机的行为,这是一个具有19种颜色、邻居半径为2的元胞自动机,通过改变它的初始条件,它就可以模拟任何一个元胞自动机。下图简示了这个通用元胞自动机的工作原理:
在这个元胞自动机中,每18个方格代表要模拟的元胞自动机的一个方格。其中在一组18个方格中第三个方格对应的是被模拟的元胞自动机第一个方格的输入(先考虑最简单的仅有两种颜色,邻居半径为1的元胞自动机),如该图示意的输入是010。剩下的2、4~16为待模拟的元胞自动机的规则编码。我们知道,对于元胞自动机来说,我们可以给它进行编码。也就是将一组同类型的元胞自动机(例如颜色数相同,半径相同)按照一定的顺序从小到大排列出来,那么每个元胞自动机对应的序号就是它的编码。反过来,给定一个编码,我们就能得到一个特定规则的元胞自动机。
因此,如果把一个元胞自动机的编码输入给通用元胞自动机,通用元胞自动机就能计算每一步的状态。通用元胞自动机所要做的就是要根据二进制的编码一个一个计算出在不同的方格输入情况下对应的输出。然后将每个待模拟方格的值与邻近的方格相互作用,得到输出的方格值。这样在经过了多步运算之后(到达虚横线所示的位置)该通用元胞自动机完成一步对被模拟元胞自动机的模拟。下面是通用元胞自动机模拟90号元胞自动机的情况:
对于更复杂的1维元胞自动机,只要扩大对应被模拟元胞自动机一组方格的个数并经过适当的转换就可以了。这样我们就能够用通用元胞自动机模拟任何一个1维的元胞自动机了。由于1维元胞自动机可以模拟任意一台图灵机,所以,该元胞自动机是通用的。
8.2 最小的通用计算系统
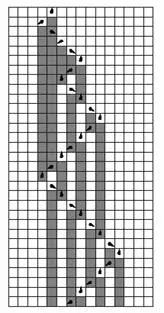
然而正如我们看到的,这个通用元胞自动机非常复杂,能不能找到一个具体的规则简单的通用元胞自动机呢?答案是肯定的,在NKS书中,这样一个目前为止最简单的支持通用计算的系统被找到了,这个发现者是Wolfram的助手Mathew Cook。他找到了一个拥有两个颜色,两个邻居的110号一维元胞自动机。下面展示了110元胞自动机在一个随机的初始条件下的行为:
我们知道,根据Wolfram的分类,这是一个第四类(复杂类型)的元胞自动机。仔细观察我们会发现,在这个元胞自动机中有许多类似“粒子”的花纹在走来走去。它们可以起到在世界的不同区域传播信息的作用。正是因为这些粒子的作用,Mathew才找到了证明它是通用的的方法。具体的,Mathew开发了一个软件工具,专门检测CA110中的粒子传播和碰撞规律。然后,它将这些粒子传播和碰撞的规律与另外一类特定的计算系统:Tag系统进行比较,发现这些粒子可以模拟Tag系统。而因为我们已知Tag系统是可以模拟任意一台图灵机的,所以这也就证明了CA110的通用性。
这个证明的意义在于,CA110是一个规则非常简单的系统。而即使规则这样简单,它仍然能够支持通用计算。一旦这个系统支持通用计算,那么它就可以完成任意一种已知的计算。
证明CA110是通用的方法也非常奇特。它并不像其它证明通用性的方法那样从底层规则做起,而是通过观察110元胞自动机涌现出的花纹上的规律出发的。因此,这是一种异常艰难的,从图形出发的证明方法。
有了110这个目前已知的最简单的通用机器之后,Wolfram甚至猜测任何一种复杂类型的元胞自动机都有可能是支持通用计算的。同时,他提出寻找最小通用机器的号召,甚至悬赏25000美元寻找能够证明一个2状态、3颜色的图灵机是通用图灵机的方法。如果能够证明此结论,那么它将是目前已知的最简单的通用图灵机。
8.3 计算等价性原理
这个证明另外一个意义还在于,它促使Wolfram提出了一个更大胆的被称为计算等价性的原理(Computational equivalence principle)。这个原理是说,任何一个行为不是很简单的系统都可能是支持通用计算的。
例如对于元胞自动机来说,还有类似110号元胞自动机的大量的第4类元胞自动机,它们可能最终都会被证明是支持通用计算的。甚至对于那些诸如30号那样的第三类(混沌类型)元胞自动机,也有可能是支持通用计算的。以至于,Wolfram都猜测,宇宙中可能根本就不存在所谓的随机性。因为一个随机的系统也有可能是支持通用计算的。
然而,事实上,这个命题目前没法证明,因为要想证明一个系统不支持通用计算要比证明它支持通用计算更困难。
这个计算等价性原理也给“万物皆有灵”的说法提供了某种支持。因为在自然界存在着各式各样的复杂过程,例如水流、化学反应等等。虽然我们很难研究这类系统,但是如果把这类过程看作一种计算过程的话,那么它们很有可能也会像110号元胞自动机那样支持通用计算。而从某种意义上说,通用计算就是宇宙中的任何一种计算,甚至我们人类大脑也不过是一种通用计算机器。那么,这些等价于通用计算的机器和自然过程从原则上讲就可以具备我们大脑一样的思考过程。因此,“万物皆有灵”的确有一定的根据。
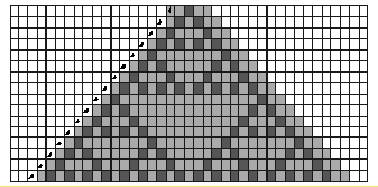
计算等价原理也为复杂性阈值的说法提供了一定的解释,如下图:
也就是说随着系统底层规则的复杂性增长,系统行为的复杂性增长到一定程度就不再增长了。这个阈值就是通用性。即当系统复杂到能够支持通用计算之后,它从原则上讲就与任何一个其它的支持通用计算的系统等价了。因此,继续增加规则的复杂性将是无济于事的。
反过来再看看前面提到的那个用元胞自动机生成的时间序列模拟股市数据的应用,我们会发现它背后的原理其实就是计算等价性。可以认为,股票市场是一个复杂的能够支持通用计算的系统,而我们知道元胞自动机也是一个支持通用计算的系统,由于它们是等价的,所以元胞自动机就能够模拟股市的时间序列,尽管真实股市的底层规则可能是各个股民的买卖操作,而元胞自动机的底层规则和真实股市的底层规则相差那么巨大。系统复杂到一定程度之后,我们就可以忘掉它的底层规则,而从另一个通用性的角度上去考虑它。因此我们的分析模式从复杂性转变到了通用性。
9.1 虚拟层级
正如Wolfram所说,计算通用性是一个非常重要的概念。然而,我认为除了计算等价性原理之外,通用计算还具有另外一个更加重要的意义,这就是“虚拟层级”的概念。
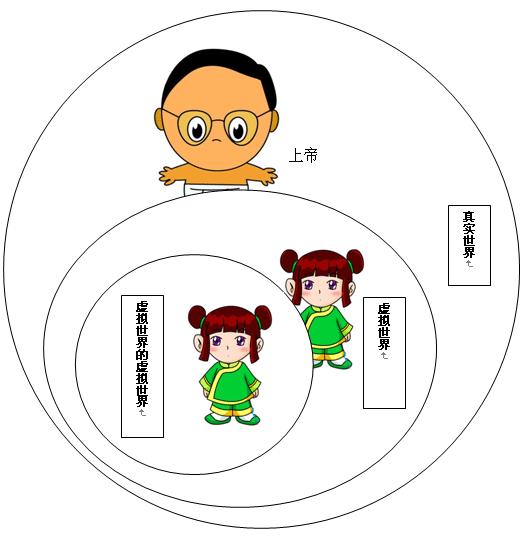
有一部类似《黑客帝国》的电影叫十三层楼。影片叙述了一个神奇的故事:一个研究虚拟世界的科学家突然被谋杀了。主人公为了调查这起凶杀案,不得不亲自走进那个科学家建立得惟妙惟肖的虚拟世界中寻找该科学家给主人公留下的一封信。信上说,他发现了一个天大的秘密:即科学家和主人公居住的世界居然也是被人虚拟出来的。主人公不相信这个事实,决定亲自验证一下。他一路开车来到了“世界的尽头”,终于看到了真相:他所生活的世界是被另一个更高层次的世界在计算机中模拟出来的。
如果我们用一个图形表示这个故事中提到的各种世界之间的逻辑关系的话,我们可以得到:
主人公所在的世界是中间一层次的世界,它是被更高一层次的造物主在一个被叫做“真实世界”的世界中创造出来的一个电脑程序。在这个虚拟世界中,那个被谋杀的科学家又创造了一个虚拟世界,我们暂且称它为虚拟世界之中的虚拟世界吧。那么这些不同的世界之间就形成了上图所示的逻辑关系。更深一层次的虚拟世界被包含在上一层次虚拟世界的模拟器之中。
实际上,我们经常会跟这种类似的虚拟层次打交道,只不过我们一般不注意罢了。比如我们在电影院看电影,那么电影里面的故事就是一个虚拟的世界,而我们是在外层的真实世界。再如我们读小说,小说也构建了一个虚拟的世界。有的电影会演出这样的内容:一群青年人正在看电影,这样电影中的电影就是更深一层次的虚拟世界。所有这些就构造了一个被我称之为“虚拟层次”的层级结构。
让我们再回到图灵机中,我们说通用图灵机可以模拟任何一个其它的计算过程。实际上,这就意味着这个通用图灵机在自己内部构造了一个虚拟的层次。如果我们记通用图灵机为U,那个被模拟的图灵机为A。那么当U模拟A的时候,实际上,A就会在U的内部形成一个像A’(例如U根据A的编码构造出来的一台抽象的虚拟机器)。因为U可以精确的模拟A的所有动作,也就是说A’会按照A的方式一模一样的行动,以至于A’根本没办法感受到它是被一个通用机器U支持的运算。同样的道理,任意的一个程序如果运行在U之中都无法感受到U的存在。因此我们说,U实际上在它的内部构造了一个全新层次的虚拟世界(比如一个运行在通用元胞自动机上面的元胞自动机110就是一个内嵌在通用元胞自动机之中的虚拟世界)。
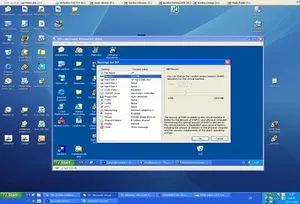
如果你对这种机器模拟机器的现象很陌生。那么我们来看一个实际的例子:有一个特殊的软件就叫做虚拟机。它是Windows中的一个程序,运行它之后,你会在Windows之上得到一个完全独立的虚拟计算机,它有虚拟的硬件、虚拟的操作系统等等。这种虚拟机器对于程序员来说有很多的好处,例如他可以在虚拟机上试验一些软件而不破坏真实计算机。虚拟机也不会害怕感染病毒,因为即使病毒再厉害它也仅仅是破坏了那台虚拟的机器,而这个虚拟的机器对于真实的计算机来说不过是一些数据罢了。下图就是一个对该虚拟机软件的截图:
该虚拟机软件运行在一个真实的Windows XP上,而虚拟机上正在运行一个 Windows XP 操作系统。
9.2 自指黑洞
因此,我们说,通用机器可以在内部构建一个完全不同的虚拟层次。下面,我们进一步想象,既然通用机器可以模拟任何一个机器,那么它能不能模拟自己呢?答案应该是肯定的,否则它就不叫做通用机器了。
然而,似乎有什么东西不对劲了。一个机器正在模拟它自己,这可能吗?我们可以想象一下,通用程序A正在读入A自己的编码,然后在内部模拟层次上创造了一个模拟的A自己。而这个模拟的A正在干什么呢?它正在读入自己的编码,而试图模拟自己。这就会造成一个无穷的怪圈。如果用图形表示的话,这就是一个无穷加深模拟层次的程序:
在理想情况下(提供给这台机器无穷大的空间和运行时间),那么我们的确会得到一个自我包含的无穷序列。它就像宇宙中的黑洞一样,会无穷延伸下去……。因此,我形象的把这样一种虚拟世界中的自指怪圈称为“计算宇宙中的黑洞”。
然而,现实的情况是,我们不能给通用机器A提供无穷的空间,因此它在内部实现的虚拟的A已经不是它自己的精确的像了。然而,有一种非常巧妙的方法,可以让A完全模拟自己的动作。这被称之为奎恩(Quine)程序,即一种能够打印出自己源代码的程序。这里的Quine是一个20世纪初的大哲学家,专门研究数理逻辑。
你一定会提出这样的质疑:这个计算宇宙中的黑洞是挺好玩的,不过也太玄乎了吧?研究它有什么用呢?呵呵,这种自指黑洞的用处可大了,早在1931年的时候,哥德尔正是用这种自指黑洞的方法证明了被美国《时代周刊》评为20世纪最伟大的数学定理:哥德尔不完全性定理。而且,出乎意料的是,冯诺依曼研究的自复制自动机理论本质上讲也具有这种自我模拟的逻辑,即自我模拟实际上是现实生命自我繁殖的逻辑基础。因此我认为,生命这类特殊的系统就是一个自我模拟的系统。可惜,这里的空间太小了,我将在另一篇文章详细论述这些奇怪的玩意儿。
Wolfram当年出版NKS这本书就遭到了各方的质疑。人们都认为他这本书中空无一物,对科学没有做出任何实质的贡献。
然而,这个判断是不完全的。这有两个原因,首先,NKS目前的研究仍处于起步阶段,Wolfram探索各种计算宇宙的目的就是要收集大量的有关虚拟宇宙的第一手观察资料。这就好比当年伽利略观察行星运动现象,他要先收集大量的数据。可以想象,当初人们观察行星运动并不能带来直接的应用。目前NKS的这些观察资料的收集也不会得到立竿见影的应用效果,这也是任何一门科学的发展规律。
其次,NKS的应用价值本身并不像我们一般人想象的那样简单。实际上,所谓的应用是和人们的需求密切相关的,新的科学技术出来了并不见得会解决一些老的问题,而是在全新的需求条件下得到了全新的应用,甚至从旧有的观点看,这些新的应用根本就不算应用。举个现实的例子就是计算机的发明,现在几乎没有任何人能够否定这是一个有用的工具。然而,在中国的一些边远山区,很多人的确还认为计算机一文不值,计算机能帮我种地吗?它能解决我的吃饭问题吗?实际上,要想看到计算机的应用价值,你必须走进信息世界这个大的环境中。
NKS也许正面临这样的处境,我怀疑,它的应用前景甚至不能用一般的评价标准来想象。例如NKS并不能帮助你找到一套合适的优化算法,它也不能帮你造出省油的机器来。然而,也许NKS可以教会你如何去设计一套虚拟世界的规则,从而使你的在线游戏更活灵活现,让人百玩不厌。因此,我们需要重新定义NKS的所谓的应用价值。
说白了,NKS是一支潜力股。那么,面对现实,就是此时此刻,我们又如何判断NKS是有潜力的呢?我的回答是,这就要看方向了,即这门新兴学科是否抓住了这个时代发展的特征。
最近有一本畅销书,叫做《世界是平的》,它在讲述悄然发生于这个世界的变化趋势,即世界正在扁平化。原有的社会体系正在被新兴的各种文化,包括互联网、博克、超级女生等现象解构。在网络上,人人都是平等的,真实世界中的那些层级关系变得完全扁平化了。超级女生的收视率远远超过了央视的春节晚会,这是因为这套节目的运作方式完全是平民对平民的。然而,世界为什么会扁平化?以前的社会层级结构为什么会解体?传统科学不能给我们带来满意解答。
也许NKS会给这个问题的解答带来一定的启发性。从某种程度上说,NKS的释放比特自由的精神非常符合这种新兴的基于个体的、扁平化的思维范式。即我们不用一种家长式的、中央控制式的办法去对付那些比特,反过来让它们自由的演化。照人们的线性思维习惯,一定会认为这样的后现代式解构会造成世界大乱,学生当起了老师,平民居然研究起了科学,小Linus居然想跟大微软抗衡。
然而,NKS中大量的计算机实验告诉我们,事情的结果是,一种自发的秩序仍然会在整体层面构造出来。而且,一旦这种涌现出的自发序复杂到一定程度以后,它又会形成一个完全崭新的虚拟层级,这个虚拟层次的出现,会引发又一轮全新的虚拟层次中的进化。
《一种新科学》作为Stephen Wolfram的开创性著作,在人工智能蓬勃发展的今天重新焕发生机。该书探讨的简单程序生成复杂性、计算普遍性和涌现行为等核心概念,与现代AI和大语言模型的基本原理高度吻合。最近社区成员韩司阳等老师积极推动《A New Kind of Science》在国内的翻译出版工作,所以集智俱乐部联合社区成员韩司阳、章彦博、徐恩峤、张江一起联合发起关于《一本新科学》的读书会,从9月1日起,每周日上午10:00-12:00开始系列的讨论,欢迎大家加入读书会,做读书会分享或者认领翻译任务。
本次读书会主要是为了聚集更多对这本书和这套理论感兴趣的探索者一起深度交流碰撞,并组织有能力的研究者一同将这本20年的经典巨作翻译成中文版;同时也是想借此机会,能够深入重读经典《A New Kind of Science》,挖掘与当前人工智能和大模型研究有着深刻联系,学习Wolfram的跨学科方法和对自然界模式的研究,为AI算法优化和系统设计提供了新视角。帮助更多的学术研究者和技术应用者从更广阔的科学哲学角度审视AI技术,深化对AI本质的理解,并可能激发解决当前AI挑战的创新思路,为探索AI的未来发展方向提供启示。
详情请见:全新读书会启动:组队研读翻译复杂科学神书,开启“一种新科学”
章彦博老师精心制作的Mathematica系列教程,它是一门简洁但又堪比「百科全书」的编程语言,非常适合新手入门,尤其是对跨学科探索感兴趣,希望快速验证一些想法。详情请见:《从 1+1 到混沌 | Mathematica 软件入门教程》
![]()
点击“阅读原文”,报名读书会